|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 6, 2007 |
УДК 621.396.96
Оценка мешающих отражений при облучении земной поверхности сверхширокополосным сигналом
С. В. Субботин, Д. Ю. Большаков
ОАО "Научно-исследовательский электромеханический институт" (ОАО "НИЭМИ")
Получена 18 мая 2007 г.
Проведена оценка время-частотных характеристик отражений от земной поверхности для активной РЛС воздушного базирования, работающей в режиме селекции движущихся наземных объектов. Рассмотрен импульсный сигнал с линейной частотной модуляцией, полная полоса которого формируется в течение ряда периодов повторения.
Для активной РЛС воздушного базирования проблема селекции движущихся наземных объектов остается одной из актуальных. Трудность ее решения состоит в том, что отражения от земной поверхности носят мешающий случайный характер и зависят от вида зондирующего сигнала. Оценка время-частотных характеристик мешающих отражений имеет важное значение при синтезе сигнала и позволяет для конкретного типа зондирующего сигнала оптимальным образом выбрать его параметры.
К современным бортовым РЛС предъявляются повышенные требования, связанные с получением высокой (сверхвысокой) разрешающей способности по дальности, что обеспечивает возможность распознавания не только класса, но и типа наземного объекта. Разрешающая способность РЛС по дальности при согласованной обработке зависит от ширины спектра зондирующего сигнала. Для получения разрешения менее 1 м ширина спектра зондирующего сигнала должна составлять более 300 МГц. Формирование сверхширокополосного зондирующего сигнала с такой мгновенной шириной спектра сопряжено со значительными трудностями. Например, используемые в современных РЛС фазированные антенные решетки имеют мгновенную полосу пропускания не более 100-120 МГц и прием сигнала с бóльшей шириной спектра связан с потерями или невозможностью решения поставленной задачи из-за искажений.
Увеличение ширины спектра зондирующего сигнала может быть достигнуто за счет изменения от периода к периоду несущей частоты импульсного сигнала и формирования спектра сигнала в течение ряда периодов зондирования. Такой способ улучшения разрешающей способности по дальности носит название межпериодного расширения спектра (МРС). Использование сигнала с МРС позволяет устранить проблему увеличения мгновенной широкополосности РЛС.
Цель работы – оценка время-частотных характеристик мешающих отражений при облучении земной поверхности импульсным зондирующим сигналом с МРС и линейной частотной модуляцией. К таким характеристикам относятся корреляционная функция отраженного сигнала и ее энергетический спектр.
Сигналы, принимаемые апертурой антенны однопозиционной РЛС, являются пространственно-временными процессами. Зависимость этих процессов от пространственных координат физически очевидна. Временная зависимость объясняется движением носителя РЛС и в общем случае переменными значениями коэффициентов отражения.
Неоднородность двумерных изображений поверхностей отражения может быть описана с помощью многомерных законов распределения, что ввиду ограниченных возможностей существующих методов анализа, как правило, недопустимо. Во многих случаях проводят анализ одномерного поля, зависящего от одной координаты и характерного для отдельных однородных участков изображений с медленно меняющимися составляющими контраста. Примером локальных физических однородностей могут служить отдельные зоны изображения: поле, лес и т.п.
Обычно полагают, что временная обработка не зависит от пространственных координат и пространственно-временная фильтрация принятого сигнала может быть разделена на две самостоятельные системы: пространственную и временную (частотную). Предположим, что на систему с линейной апертурой антенны длиной L поступает нормально распределенный элементарный сигнал, характеризующийся круговой частотой
и угловой координатой
. Используя методы теории оценки параметров сигнала [1], можно показать, что коэффициент корреляции совместных измерений частоты
и угловой координаты
равен
где
- время обработки сигнала,
- скорость распространения радиоволн.
Из формулы (1) следует, что коэффициент корреляции и взаимозависимость измерений частоты
и угловой координаты цели
существенным образом определяются параметром
, представляющим собой отношение времени прохождения фронтом электромагнитной волны пространства, занимаемого апертурой антенны, к продолжительности обработки сигнала. Для рассматриваемой РЛС параметр
, что свидетельствует о независимости частотных (временных) и пространственных измерений сигналов.
Примем, что РЛС движется равномерно и прямолинейно со скоростью
(рис. 1). За время
локатор перемещается на расстояние
, а элементарный отражатель – на расстояние
, где
- радиальная составляющая скорости отражателя относительно РЛС. Из рис. 1 следует, что радиальные смещения отражателей равны
,
где
.
Рис. 1. Облучение земной поверхности
Замена пространственного смещения
временным смещением
означает переход от пространственных флюктуаций к временным и от пространственно-временной корреляционной функции к временной. При облучении объемно-распределенной цели пачкой импульсов нормированную корреляционную функцию можно представить в виде [2]
В формуле (2)
где
- комплексная огибающая высокочастотного импульса на входе приемника,
-есть доплеровская частота для отражателя с угловыми координатами
.
Множитель
формулы (2) равен
где
- нормированная (
) двумерная диаграмма направленности антенны (ДНА) по мощности.
Множитель
формулы (5) равен
В выражении (2) нормирующий множитель
определятся из уравнения радиолокации [3]:
,
где
- мощность излученного сигнала;
- длина волны;
- углы, определяющие положение отражателя в пространстве относительно плоскости поляризации и направления луча ДНА;
- характеристика, выражающая зависимость амплитуды отраженного сигнала от ориентации отражателя в пространстве;
- эффективная площадь рассеяния отражателя при фиксированных значениях углов
;
- расстояние отражателя от РЛС в момент времени
.
В соотношении (2) сомножитель
учитывает флюктуации, связанные с распространением периодических импульсов внутри объемно-распределенной цели (флюктуации по дальности, или быстрые флюктуации), сомножитель
учитывает флюктуации, вызванные различием радиальных скоростей движения отражателей относительно РЛС (доплеровские флюктуации, или медленные флюктуации). При этом функция
- периодическая, а функция
- непериодическая, а их произведение не является периодической функцией, так как «зубцы» функции
с увеличением
уменьшаются из-за доплеровских флюктуаций, которые тем сильнее разрушают корреляцию, чем больше число
.
Рассмотрим нормированные корреляционные функции
и
раздельно.
Пусть РЛС излучает сигнал, который является пачкой когерентных прямоугольных импульсов длительностью
с периодом следования
:
где
.
Для вычисления нормированной корреляционной функции
сигнала на входе приемника определим произведение двух смещенных относительно друг друга последовательностей импульсов:
,
где
,
,
- расстояние от антенны до элементарного отражателя,
- изменение величины
из-за движения носителя РЛС или отражателя,
- знак сопряжения.
При фиксированной величине
результирующий сигнал является суммой элементарных сигналов, принятых от всех отражателей, расположенных в пределах облучаемой зоны. Учитывая, что
, обозначая через
индекс суммирования для сигнала
, а через
индекс суммирования для сигнала
, и полагая
, находим с учетом соотношения (7)
. (8)
В выражении (8) учтено, что для когерентных импульсов
. Функция (8) является периодической по двум переменным:
и
, где
- относительный сдвиг двух импульсных последовательностей. Используя соотношение (8), при исключении суммирования по величине
получаем значение нормированной корреляционной функции сигнала на входе приемника:
. (9)
В соотношении (9) нормированная корреляционная функция
есть периодическая функция с периодом
, состоящая из узких «зубцов», ширина которых определяется протяженностью функции
, т.е. длительностью импульсов
. При
значение функции
в формуле (9) отлично от нуля, так как импульсы, смещенные на величину
, частично перекрываются. По мере увеличения значения
перекрытие импульсов уменьшается и корреляция постепенно исчезает. Когда
, перекрытие отсутствует и функция
. Таким образом, интервал корреляции флюктуаций по дальности близок к длительности импульса. Если увеличивать длительность
до величины периода повторения
, то между сигналами вновь появится корреляция, поскольку сигнал в следующем периоде приближенно повторяет сигнал в предыдущем периоде. Естественно, корреляция восстанавливается не полностью и ее разрушение связано с движением РЛС. Это учитывается в нормированной функции корреляции
, представленной в уравнениях (2)-(5).
При движении РЛС в соотношении (4) величина
и корреляция достигает максимума при значении
, когда сопоставляются сигналы, принятые от одного и того же импульсного объема, сместившегося за время
на расстояние
. При
наблюдается сжатие, а при
- растяжение временного масштаба в
раз, которые объясняются доплеровским эффектом.
Форма и ширина нормированной корреляционной функции
в выражении (9) определяются формой и длительностью излучаемых импульсов. Пусть РЛС излучает импульсы прямоугольной формы с линейной частотной модуляцией (ЛЧМ) и межпериодным расширением спектра (МРС). Сигнал с ЛЧМ и МРС можно представить в виде
где
,
,
- девиация частоты за время импульса
.
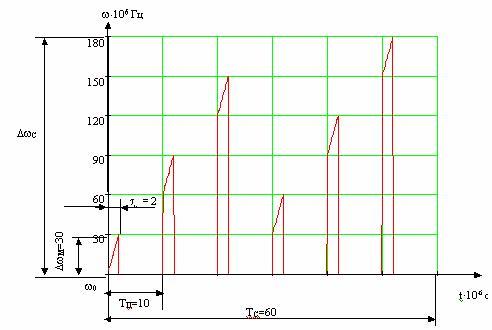
Изменение частоты модуляции импульсного сигнала при
=150 от времени представлено на рис. 2.
Рис. 2. Изменение частоты модуляции импульсного сигнала с ЛЧМ и МРС
приот времени
Подставляя соотношение (10) в формулу (9), при
получаем значение нормированной корреляционной функции
График нормированной корреляционной функции
для различных значений
при
представлен на рис. 3.
Рис. 3. Нормированная корреляционная функция флюктуаций по дальности для
ЛЧМ-импульса прямоугольной формы прив зависимости от
величины
Из выражения (11) следует, что при
и
нормированная корреляционная функция
приближается к функции sinc
, которая показана на рис. 3 штриховой линией. При неограниченном увеличении значения
интервал корреляции стремится к величине
, т.е. каждый "зубец" нормированной корреляционной функции флюктуаций по дальности
определяется девиацией частоты в импульсе сигнала с МРС, что эквивалентно укорочению излучаемого импульса до длительности
, т.е. уменьшению в
раз, что согласуется с известным фактом улучшения разрешающей способности по дальности для сигнала с ЛЧМ [3].
Спектр флюктуаций по дальности может быть получен в результате обратного преобразования Фурье соотношения (11):
где
,
- интегралы Френеля.
Интервал корреляции представляет собой величину, обратную эффективной ширине огибающей спектра, и с учетом выражения (12) равен
.
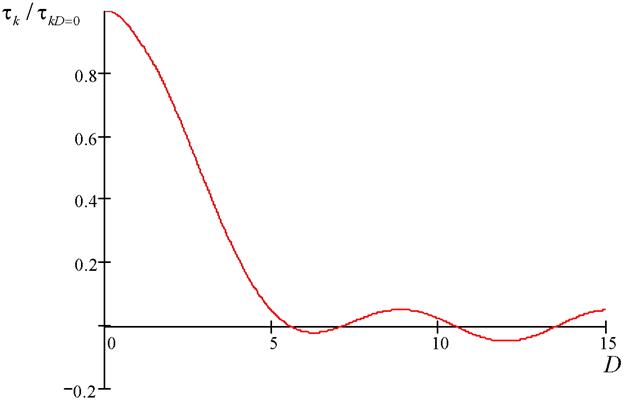
На рис. 4 показан график изменения нормированного интервала корреляции флюктуаций по дальности в зависимости от величины
для импульса прямоугольной формы. В качестве нормирующего множителя выбрано значение интервала корреляции при отсутствии модуляции, т.е. при
.
Рис. 4. Нормированный интервал корреляции по дальности для ЛЧМ-импульса прямоугольной формы в зависимости от значений
Доплеровские флюктуации описывает нормированная корреляционная функция
, представленная в формуле (5), которая в выражении (2) является огибающей функции
и характеризует межпериодные флюктуации.
Предположим, что ось ДНА отклонена от линии движения РЛС
(см. рис. 1) настолько, что, по крайней мере, один из углов (или
) больше ширины ДНА в соответствующей плоскости. При этом, если считать ДНА узкой, можно разложить функцию (6) в ряд Тейлора, ограничиваясь линейными членами:
где
- доплеровская частота, соответствующая центру импульсного объема в направлении вдоль оси ДНА, и
;
- доплеровская частота в горизонтальной плоскости (угол
);
- доплеровская частота в вертикальной плоскости (угол
).
С помощью аппроксимации представим комплексную функцию ДНА
в виде суммы двух действительных функций, области определения которых не пересекаются. Эти функции характеризуют главный и боковые лепестки ДНА:
где
- ДНА главного лепестка,
- ДНА боковых лепестков.
Представленные в формуле (14) функции ДНА достаточно просто сопоставляются с экспериментально снятой ДНА. При этом необходимо отдельно аппроксимировать главный и боковые лепестки ДНА.
При вычислении нормированной корреляционной функции
согласно выражению (5) с учетом соотношения (14) появляется произведение вида
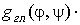
,
которое отлично от нуля лишь вблизи границы этих функций. Учитывая абсолютную малость изменения функций, характеризующих главный и боковые лепестки ДНА в области определения рассматриваемого произведения, можно считать
и отнести произведение указанного вида к области определения главного лепестка.
Предположим, что в соотношении (14) выполняется условие разделения переменных. Тогда можно записать
где
- ДНА соответственно в горизонтальной (угол
) и вертикальной (угол
) плоскостях.
Подставляя выражения (13), (15) в формулу (5), получаем
где
,
- частные нормированные корреляционные функции, которым соответствуют спектры
и
.
С физической точки зрения спектр
совпадает по форме с квадратом ДНА в горизонтальной плоскости, проходящей через линию движения РЛС и ось диаграммы излучения. Частота
сигнала, принятого от некоторого элементарного отражателя, отличается от частоты излучения
на доплеровскую частоту
,
где
- угол между направлением движения РЛС и направлением на данный элементарный отражатель.
При
всем отражателям, расположенным на поверхности конуса, ось которого совпадает с направлением движения РЛС, а угол при вершине равен
, соответствует одинаковая доплеровская частота. В образовании сигнала с фиксированной доплеровской частотой, принимаемого в некоторый момент времени, участвуют отражатели, расположение которых ограничено конусом и импульсным объемом, равным (
,
). В среднем мощность сигнала с данным доплеровским сдвигом, а значит, и спектральная плотность равны сумме мощностей элементарных сигналов одинаковой доплеровской частоты. Спектральная плотность будет зависеть от квадрата коэффициента усиления антенны в направлении оси излучения. Спектр
будет совпадать по форме с квадратом ДНА по мощности:
Частота, соответствующая максимуму спектральной мощности, равна
.
При аппроксимации главного лепестка ДНА гауссовской кривой выражение (17) принимает вид
где
,
- эффективная ширина ДНА по мощности соответственно в горизонтальной и вертикальной плоскостях.
С учетом формулы (18) соотношение (16) имеет вид
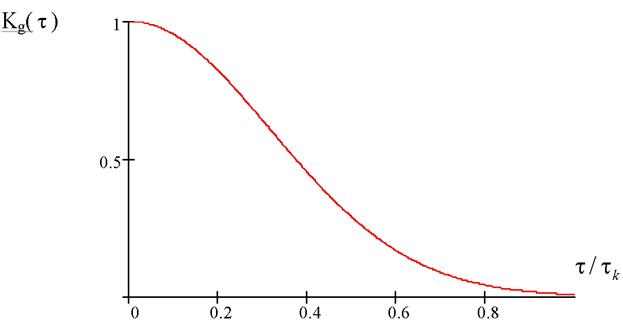
График нормированной корреляционной функции
, полученной из выражения (19), представлен на рис. 5.
Рис. 5. Нормированное значение корреляционной функции доплеровских флюктуаций для гауссовской диаграммы направленности антенны при
в зависимости от величины
.
Для импульсного зондирующего сигнала, помимо рассмотренных выше быстрых и медленных флюктуаций, появляются флюктуации, связанные с перемещением импульсного объема отражателей из-за движения РЛС. Такие флюктуации обычно называют флюктуациями из-за смены отражателей.
Рассмотрим корреляцию для моментов времени
, отстоящих друг от друга на
периодов повторения
и фиксированных относительно момента излучения импульса. Из соотношений (2)-(5) следует, что
где
,
.
Из формулы (20) видно, что при фиксированной дальности нормированная корреляционная функция межпериодных флюктуаций равна произведению функции
, которая является функцией межпериодных флюктуаций при скользящей дальности, и функции
, которая является функцией внутрипериодных флюктуаций с сильно растянутым масштабом. Интервал корреляции флюктуаций, связанных со сменой отражателей, равен времени, необходимому для того, чтобы импульсный объем, движущийся со скоростью
, полностью обновился. При излучении прямоугольных импульсов сигнала с ЛЧМ и МРС с девиацией
интервал корреляции равен
Из равенства (21) следует, что интервал корреляции рассматриваемого-сигнала уменьшается в
раз по сравнению с немодулированным сигналом, а ширина спектра соответственно увеличивается в
раз.
При произвольном значении
спектр флюктуаций из-за смены отражателей совпадает с огибающей спектра флюктуаций по дальности в выражении (12) и при
стремится к прямоугольной форме.
Полная нормированная корреляционная функция
сигнала с ЛЧМ и МРС в выражении (20) при
совпадает с нормированной корреляционной функцией
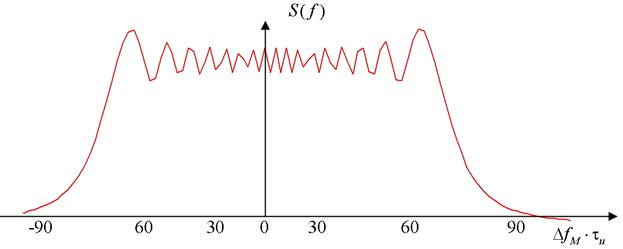
в формуле (10) и показана на рис. 3. Огибающая спектра флюктуаций
, соответствующая нормированной корреляционной функции
, представлена на рис. 6. При малом значении боковых лепестков ДНА влиянием "хвостов" спектра можно пренебречь. При этом ширина прямоугольного спектра мешающих отражений от земной поверхности для сигнала с ЛЧМ и МРС в основном зависит от флюктуаций из-за смены отражателей и значений
в каждом импульсе.
Рис. 6. Огибающая спектра флюктуаций сигнала с ЛЧМ и МРС для импульса
прямоугольной формы при
Выбор величины
в зондирующем сигнале с ЛЧМ и МРС определяет ширину спектра мешающих отражений, оценка которой дает возможность выбрать полосу режекции. Успешная режекция мешающих отражений и частотная селекция позволяет повысить вероятность правильного обнаружения движущихся наземных объектов РЛС воздушного базирования.
Литература
Куликов Е.И., Трифонов А.П. Оценка параметров сигнала на фоне помех. – М.: Сов. радио, 1978.
Фельдман Ю.И., Мандуровский И.А. Теория флуктуаций локационных сигналов, отраженных распределенными целями. / Под ред. Ю.И. Фельдмана. – М.: Радио и связь, 1988.
Радиолокационные системы многофункциональных самолетов. Т.1. РЛС – информационная основа боевых действий многофункциональных самолетов. Системы и алгоритмы первичной обработки радиолокационных сигналов. / Под ред. А.И. Канащенкова и В.И. Меркулова. – М.: Радиотехника, 2006.
Авторы:
Субботин Сергей Валентинович, Большаков Денис Юрьевич zuml@mail.ru
ОАО "Научно-исследовательский электромеханический институт" (ОАО "НИЭМИ")


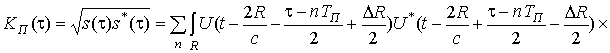
 . (11)
. (11)
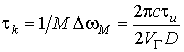 . (21)
. (21)