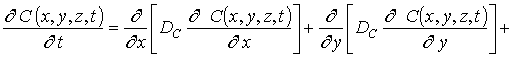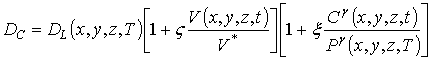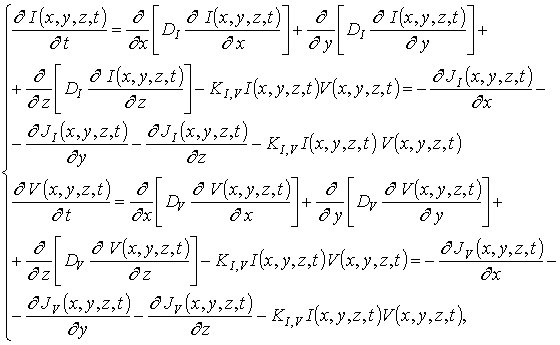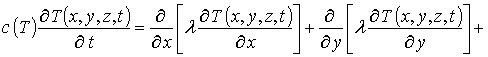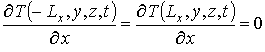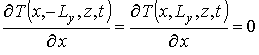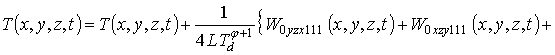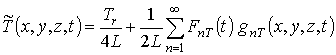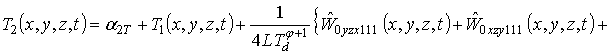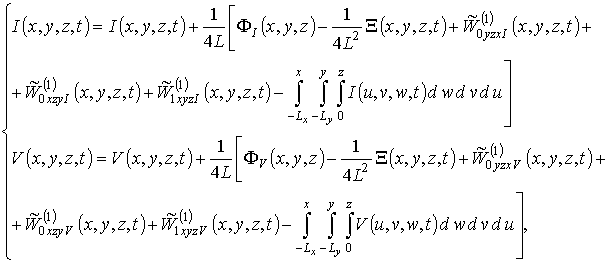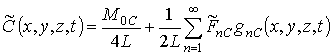Уменьшение глубины залегания элементов системы имплантационных p-n-переходов и увеличение степени интеграции их системы оптимизацией неоднородности и отжига легируемой структуры

 Е. Л. Панкратов
Нижегородский архитектурно-строительный университет

Получена 15 мая 2010 г.

 

Аннотация. Ранее было показано (см., например, [1-3]), что выбором параметров многослойной структуры, а также оптимизацией длительности отжига можно уменьшить глубину залегания одиночных диффузионных и имплантационных p-n-переходов, сформированных в такой структуре, по сравнению с p-n-переходами, сформированных в однородных образцах. Аналогично можно увеличить степень интеграции p-n-переходов, являющихся элементами интегральных схем (см., например, [4]). Данная работа посвящена анализу перераспределения примеси в процессе формирования систем имплантационных p-n-переходов (биполярных транзисторов и тиристоров) в многослойных структурах с целью поиска условий, при которых происходит одновременное (в течении одного технологического этапа) уменьшение пространственных размеров p-n-переходов (как глубины залегания, так и степени интеграции p-n-переходов, являющихся элементами интегральных схем).

 

Ключевые слова: уменьшение глубины залегания имплантационных p-n-переходов, увеличение степени интеграции системы имплантационных p-n-переходов, оптимизация отжига.

Введение

Одной из проблем производства устройств твердотельной электроники является увеличение степени интеграции элементов интегральных схем (ИС), а также уменьшение глубины залегания таких их элементов, как p-n-переходы, так и их системы [5-7]. Вторая из перечисленных проблем представляет интерес и для дискретных аналогов рассмотренных элементов ИС. Еще одной актуальной проблемой является интерес уменьшение разогрева устройств твердотельной электроники в процессе их функционирования. Для уменьшения пространственных размеров диффузионных и имплантационных p-n-переходов и их систем, как входящих в состав ИС, так и их дискретных аналогов используются различные методы. К уже отработанным методам относятся формирование неоднородного распределения температуры (лазерным, микроволновым и другими аналогичными типами отжига) [8,9], а также формирование неоднородного распределения дефектов (например, радиационных) легируемой структуры [10,11]. Оба способа приводят к неоднородности свойств легируемой структуры (например, к неоднородности коэффициента диффузии примеси при её диффузионной разгонке), что и позволяет уменьшить пространственные размеры p-n-переходов. Ранее было показано (см., например, [1-3]), что формирование диффузионных и имплантационных p-n-переходов в многослойных структурах (МС) при подобранных определенным образом ее параметрах и оптимальном значении длительности отжига формируется более компактное распределение примеси по глубине МС и более равномерное ее распределение в обогащенной ею области. Второе из перечисленных следствий позволяет уменьшить локальные разогревы легированной структуры в процессе функционирования сформированных на ее основе устройств. Первое следствие позволяет уменьшить глубину залегания p-n-переходов за счет увеличения его резкости при фиксированной величине допуска на локальный разогрев структуры. Данное увеличение его резкости позволяет снизить диффузионную составляющую емкости p-n-перехода, что приводит к увеличению его быстродействия. Предложенный способ уменьшения глубины залегания диффузионных и имплантационных p-n-переходов может использоваться как альтернативный к уже существующим, так и дополняющий их [12,13]. В [4] показано, что рассмотренный в [1-3] способ после соответствующего усложнения может быть использован для увеличения степени интеграции p-n-переходов, входящих в состав ИС.

Основной целью данной работы является анализ возможности одновременного уменьшения пространственных размеров являющихся элементами ИС всех имплантационных p-n-переходов, входящих в состав биполярных транзисторов и тиристоров. Для решения поставленной цели рассмотрим две МС (обозначим их как МС₁ и МС₂), состоящие соответственно из двух или четырех эпитаксиальных слоев (ЭС), которые далее будем обозначать как ЭС_i (), и подложки с заданным типом проводимости (n или p). Слои рассматриваемых МС имеют толщины соответственно a₁ (0£ z£ a₁), a₂-a₁ (a₁£ z£ a₂) и L_z-a₂ (a₂£z£L) (для МС₁) и a₁ (0£ z£ a₁), a₂-a₁ (a₁£ z£ a₂), a₃-a₂ (a₂£ z£ a₃), a₄-a₃ (a₃£ z£ a₄) и L-a₄ (a₄£ z£L_z) (для МС₂). 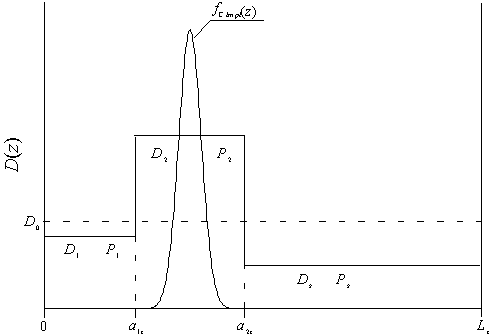Данные структуры представлены соответственно на рис. 1 и рис. 2. Будем считать, что ЭС₁ и ЭС₃ имеют тип проводимости, совпадающий с типом проводимости подложки. 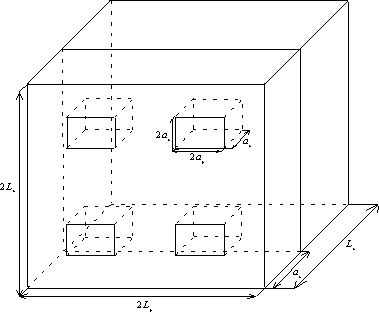Эпитаксиальные слои рассматривались как многоматериальные. В каждом из них сформированы области из других материалов, равные толщинам ЭС (см. рис. 3). В данные области имплантируется примесь, принимающая к моменту окончания данной технологической операции распределение f_C(x,y,z) приведенными (см. рис. 1 и 2). В случае рис. 2 примесь имплантируется с различными энергиями, что и позволяет сформировать распределение примеси с двумя максимумами. Далее проводится отжиг радиационных дефектов, приводящий к уширению начального распределения примесей. При этом представляет интерес следующая ситуация: (i) проводится импульсный лазерный отжиг радиационных дефектов, обеспечивающий локальность прогрева легируемых структур [14-16]; (ii) коэффициенты диффузии примеси в эпитаксиальных слоях D_i (обозначим коэффициенты диффузии эпитаксиальных слоев через D_ia, а коэффициенты диффузии “вставок” в эпитаксиальные слои через D_ib) и подложки D_s, а также растворимости примеси в эпитаксиальных слоях P_i (обозначим растворимости примеси в эпитаксиальных слоях через P_ia, а растворимости примеси в “вставках” в эпитаксиальных слоях через P_ib) и подложки P_s удовлетворяют следующим условиям: D₁,D₃,D_s<D₂,D₄; D_ia<D_ib; P₁,P₃,P_s <P₂,P₄; P_ia<P_ib; (iii) соотношение между энергиями имплантированных ионов и толщинами ЭС таково, что после отжига радиационных дефектов примесь достигает или почти достигает ближайших границ раздела между слоями МС. Далее для решения поставленной цели проведем анализ перераспределения примеси в рассматриваемой МС. Сопутствующей целью является развитие математического аппарата для данных задач. Такое развитие позволяет повысить точность теоретического описания технологических процессов, что приводит к повышению их предсказуемости и, как следствие, позволяет повышать воспроизводимость характеристик твердотельных устройств.

 

Рис.1. МС₁, содержащая два ЭС (zÎ[0,a_1z], zÎ[a_1z,a_2z]) и подложку (zÎ[a_2z,L_z]). На данном рисунке также приведено начальное распределение примеси.

 

 

 

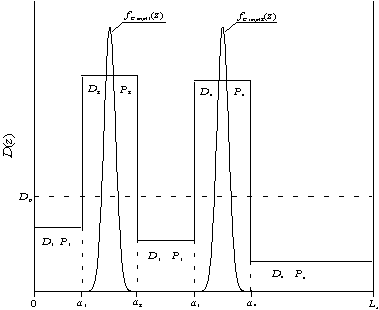
Рис.2. МС₂, содержащая три ЭС (zÎ[0,a_1z], zÎ[a_1z,a_2z], zÎ[a_2z,a_3z]) и подложку (zÎ[a_3z,L_z]). На данном рисунке также приведены начальные распределения примесей.

 

 

 

Рис.3. Структура многоматериальных эпитаксиальных слоев в направлении,

перпендикулярном направлению введения примеси

Методика анализа

Динамика перераспределения примесей в приведенных на рис. 1 и 2 МС описывалась вторым законом Фика в следующей форме [5-7]

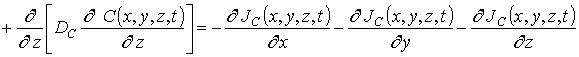, (1)

где C(x,y,z,t) – пространственно-временное распределение примеси; J_С(x,y,z,t) – пространственно-временное распределение потока примеси; D_С – коэффициент диффузии примеси, величина которого зависит от динамических свойств примеси в материалах слоев многослойныx структур, скорости прогрева и охлаждения многослойныx структур, а также от пространственно-временного распределения концентрации примеси и радиационных вакансий V(x,y,z,t) с их равновесным распределением V^*. Зависимость коэффициента диффузии от концентраций примеси и радиационных вакансий может быть аппроксимирована полиномами следующего вида (см., например, [7,17,18])

,                (2)

где D_L(x,y,z,T) – коэффициент диффузии примеси при низком уровне легирования; T - температура; P(x,y,z,T) – предел растворимости примеси; определяемый свойствами материала параметр g может принимать целые значения, как правило, в интервале g Î[1,3] (это свойство подробно описано в [7]). Концентрация радиационных вакансий может быть описана следующей системой уравнений [19]

  (3)

где I(x,y,z,t) концентрация радиационных междоузельных атомов с их равновесным распределением I ^*. K_I,V(x,y,z,T) – параметр рекомбинации (реакции), зависящий, как и коэффициенты диффузии междоузельных атомов D_I (x,y,z,T) и вакансий D_V (x,y,z,T), от свойств материалов многослойных структур и температуры. Далее рассмотрим отжиг примеси и радиационных дефектов.

Пространственно-временное распределение температуры может быть описано с помощью соответствующего закона Фурье [20]

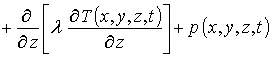,                               (4)

где l(x,y,z,T) - коэффициент теплопроводности, значение которого зависит как от свойств отжигаемого материала, так и от температуры. Температурная зависимость коэффициента теплопроводности в искомой области температур может быть аппроксимирована следующим образом: l(x,y,z,T)=l_ass(x,y,z)[1+m T_d^j/T^j(x, y,z,t)] (см., например, [20]). c(T)=c_ass[1-J exp(-T(x,y,z,t)/T_d)] –теплоемкость материала; T_d – температура Дебая [20]. В наиболее интересующем нас случае является сопоставимой по величине с температурой Дебая или превышает ее, что позволяет считать: c(T)»c_ass. p(x,y,z,t) – выделяющаяся в МС объемная плотность мощности.

Уравнения (1), (3) и (4) необходимо дополнить граничными и начальными условиями, которые могут быть представлены в следующем виде

; ;

; ;

; ;

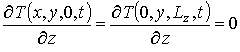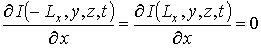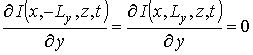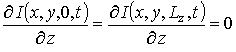C(x,y,z,0)=f_C(x,y,z); I(x,y,z,0)=f_I(x,y,z)=I^*;

V(x,y,z,0)=f_V(x,y,z)=V^*; T(x,y,z,0)=f_T(x,y,z)=T_r;                         (5)

; ;

; ;

; ,

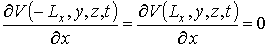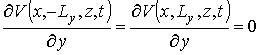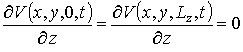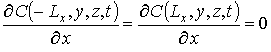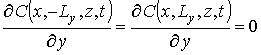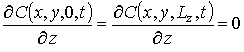где T_r –совпадающая с комнатной равновесная температура.

На первом этапе проведем оценку температурного поля. В общем случае решения уравнения (4) неизвестно. Для получения приближенного решения представим уравнение (4) в следующей форме

     (6)

,

 

 

 

 ;

 

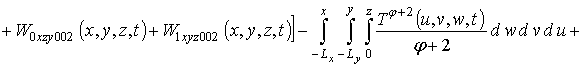
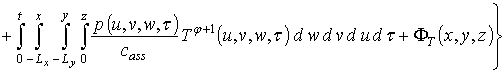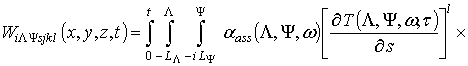
где{L,Y,w}={x,y,z},

 

  

;

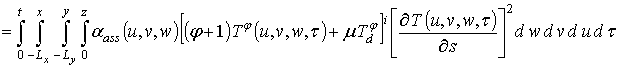 L=L_xL_yL_z.

Решение уравнения (6) будем искать методом осреднения функциональных поправок [21] с уменьшенным количеством итерационных шагов [22]. Для уменьшения количества итерационных шагов для достижения требуемой точности целесообразно выбиралось более точное исходное приближение пространственно-временного распределения температурного поля. В качестве более точного исходного приближения выберем решение уравнения (4), соответствующее усредненному по координате коэффициенту температуропроводности a_0ass и нулевому значению параметра m. Такое решение может быть представлено в виде суммы следующего ряда

,                          (7)

где

,

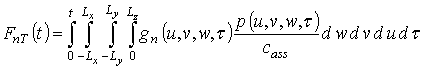g_nT(x,y,z,t)=c_nx(x)c_ny(y) c_nz(2z)e_nT(t),

 ,

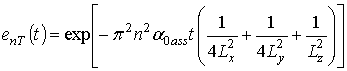c_nc(c)=cos(p nc/2L_c).

 

Подстановка соотношения (7) в правую часть уравнения (6) вместо функции T(x,y,z,t) позволяет получить ее первое приближение по модифицированному методу осреднения функциональных поправок, приведенное из-за громоздкости в приложении. Второе приближение температуры T₂(x,y,z,t) по модифицированному методу осреднения определим в рамках стандартной процедуры (см., например, [21]), т.е. путем замены функции T(x,y,z,t) в правой части уравнения (6) на следующую сумму: . Такая замена позволяет получить

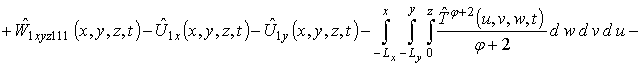
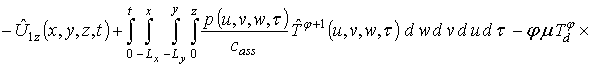  (8)

,

где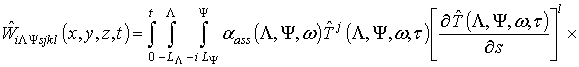  

_;

 

.

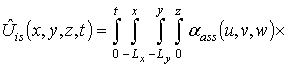
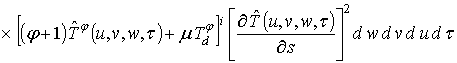Параметр a_2T определяется следующим соотношением [21]

a_2T =(M_2T - M_1T)/4LQ,                                           (9)

где 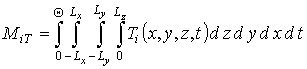. Подстановка (8) в (9) позволяет получить следующий полином, корнями которого является параметр a_2T

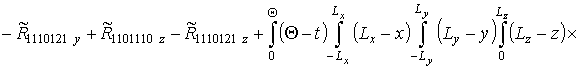                   (10)

,

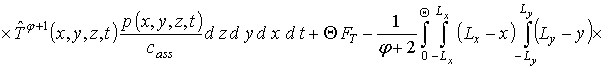
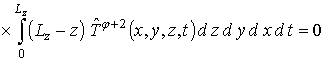где

 ;

;

.

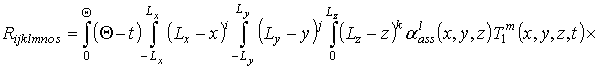
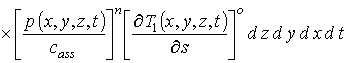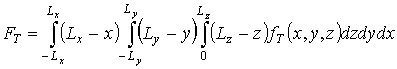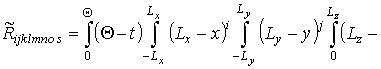
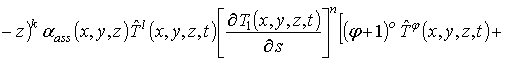
В качестве примера для некоторых значений j получены следующие соотношения для параметра a_2T

j =1

,

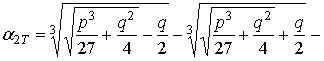
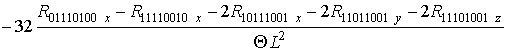где

;

;

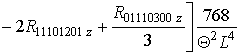j =2

,

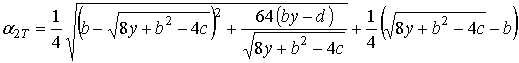где

,

 ;

 

;

 

;

 

.

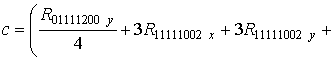
Для проведения качественного анализа и некоторых количественных оценок часто достаточно второго приближения по методу осреднения функциональных поправок (см., например, [12,13,22]). По этой причине при оценке температурного поля, а также концентраций примеси и радиационных дефектов ограничимся соответствующими вторыми приближениями.

Далее проведем оценку пространственно-временного распределения радиационных дефектов. Для этого системе дифференциальных уравнений (3) поставим в соответствие систему эквивалентных интегро-дифференциальных уравнений

(11)

где

,

 .

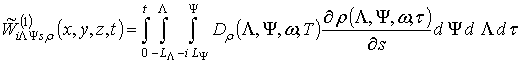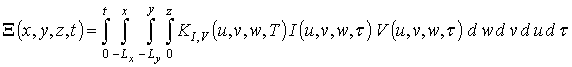Решение данной системы определим с помощью метода осреднения функциональных поправок с уменьшенным количеством итерационных шагов. В качестве исходных приближений выберем следующие соотношения

, ,

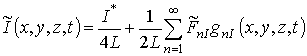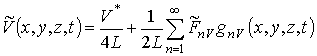где

,

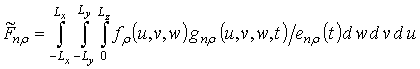g_nTr(x,y,z,t)=c_nx(x)c_ny(y) c_nz(2z)e_nr(t),

.

 

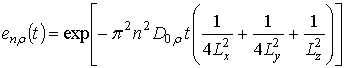Подстановка выбранной формы исходного приближения в правую часть системы уравнений (11) позволяет получить следующий результат

,

,

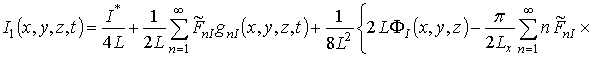
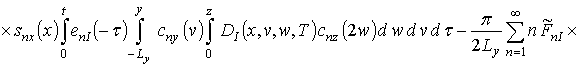
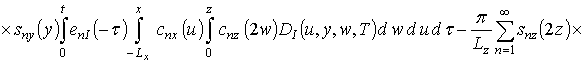
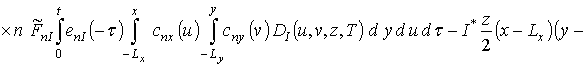
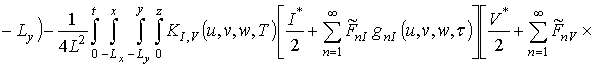
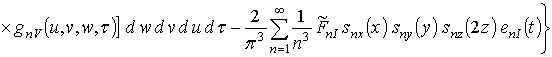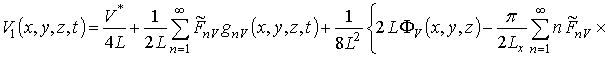
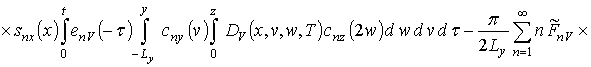
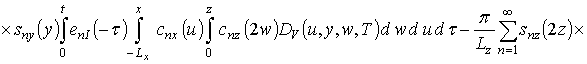
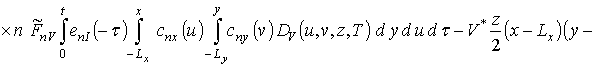
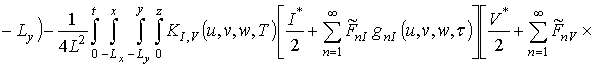
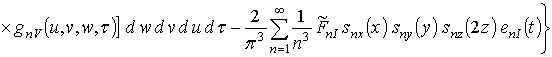где s_nc(c)=sin(p nc/2L_c).

Вторые приближения концентраций радиационных дефектов I₂(x,y,z,t) и V₂(x,y,z,t) по модифицированному методу осреднения определим в рамках стандартной процедуры, т.е. путем замены функций I (x,y,z,t) и V (x,y,z, t) в правых частях уравнений (11) на следующие суммы: I (x,y,z,t)®a_2I+I₁(x,y,z,t) и V (x,y,z,t) ®a_2V+V₁(x,y,z,t). Такая замена позволяет получить

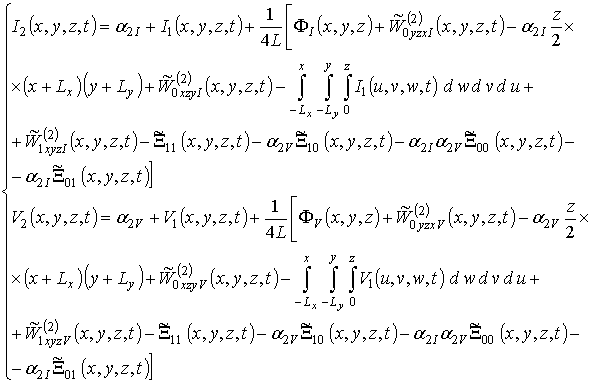
где

,

 .

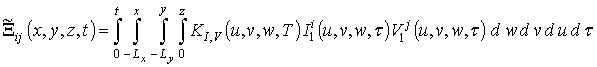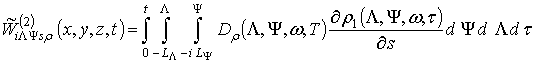Параметры a_2I  и a_2V определяется следующим соотношением

a_2r =(M_2r - M_1r)/4LQ, a_2r =(M_2r - M_1r)/4LQ,                                         (12)

где

.

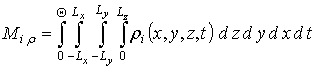M_0r и M_0C  будем считать, соответственно, полным количеством радиационных дефектов или примеси. Подстановка вторых приближений концентрации радиационных дефектов в (12) позволяет получить следующее соотношение

,

,

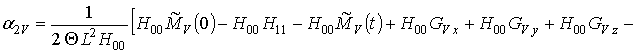
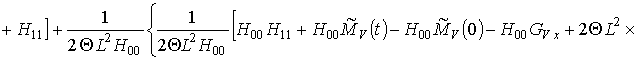
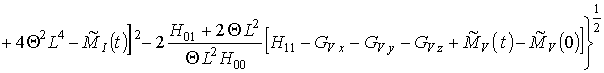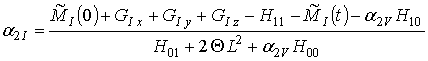где

;

;

.

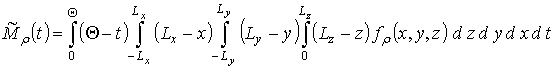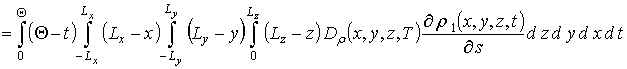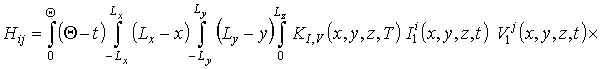
Используя оценки пространственно-временного распределения температурного поля и концентрации радиационных дефектов проведем анализ динамики перераспределения примеси в рассматриваемой структуре. Для этого поставим в соответствие уравнению (1) следующее интегро-дифференциальное уравнение

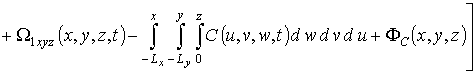.         (13)

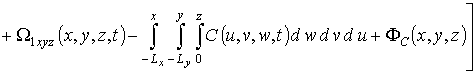
где

 .

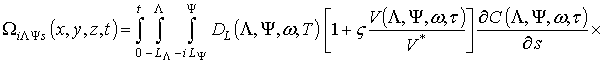
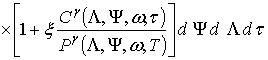Для определения пространственно-временного распределения концентрации примеси также воспользуемся модифицированным ранее методом осреднения функциональных поправок. В качестве исходного приближения выберем решение уравнения (1), соответствующее среднему значению коэффициента диффузии D_0L, т.е.

.                       (14)

Подстановка (14) в (13) позволяет получить первое приближение концентрации примеси по методу осреднения в следующей форме

.

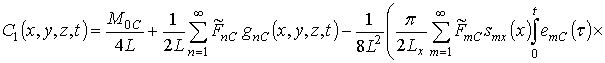
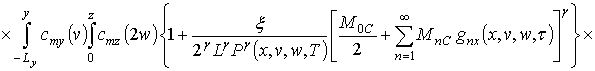
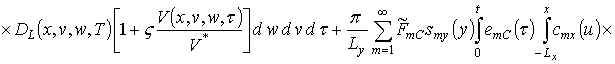
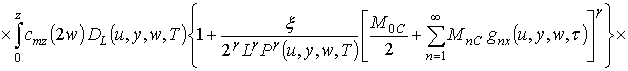
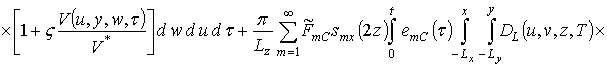
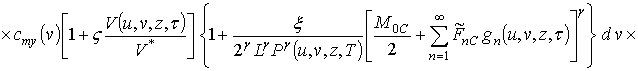
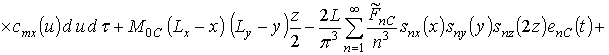
Расчет второго приближения концентрации примеси по методу осреднения приводит к следующему результату

.

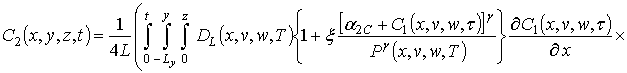
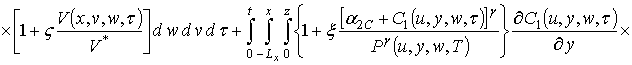
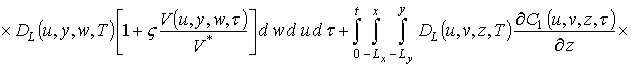
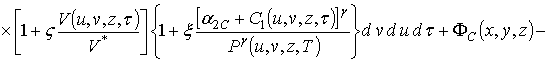
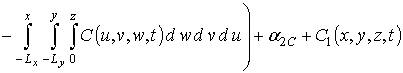Подстановка второго приближения концентрации примеси в соотношение, аналогичное соотношениям (9) и (12), позволяет получить

.

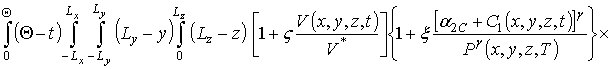
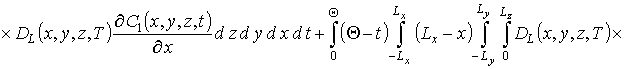
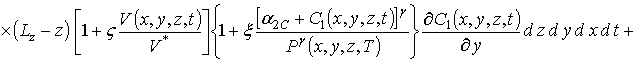
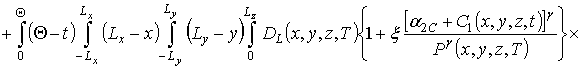
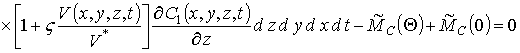В качестве примера для некоторых значений g  получены следующие соотношения для параметра a_2C

g =1

,

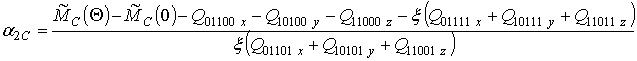где

 ;

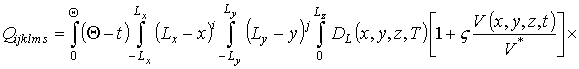
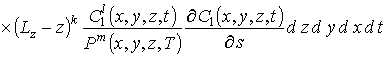g =2

,

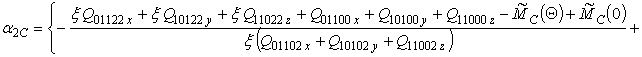
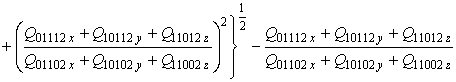g =3

,

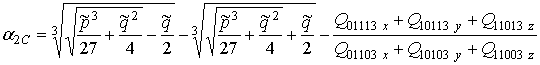где

;

 

.

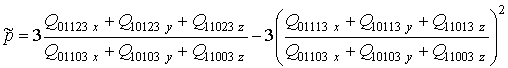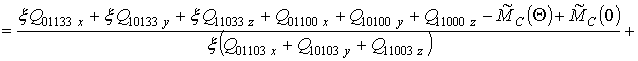
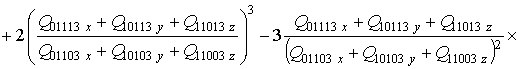
Далее проведем анализ динамики перераспределения примеси в рассмотренных МС. Полученные аналитические соотношения позволяют провести наглядное исследование динамики перераспределения примеси в процессе ее отжига. Использование численных методов позволяет уточнить полученные результаты. По этой причине в дополнение к аналитическим использовались также и численные методы решения уравнений (1), (3) и (4).

Результаты анализа

Проведем анализ динамики перераспределения примеси в рассмотренной МС в приближении пренебрежимо малой ширины переходной области между слоями. В таком приближении пространственные зависимости коэффициентов диффузии и теплопроводности без учета нелинейных эффектов для одной вставки нового материала в ЭС могут быть аппроксимированы следующими функциями: a_ass(x,y,z)=a_ass1a[1(x+a_x)-1(x-a_x)][1(y+a_y) -1(y-a_y)][1(z)-1(z-a_z1)]+a_ass2a 1(x+a_x)-1(x-a_x)][1(y+a_y)-1(y-a_y)][1(z-a_z2)-1(z-a_z1)]+a_ass3a[1(x+a_x)-1(x-a_x)][1(y+a_y)-(y-a_y)]1(z-a_z2)+a_ass1b1(x-a_x)1(y-a_y)[1(z)-1(z-a_z1)]+a_ass2b1(x-a_x)1(y-a_y)[1(z-a_z2)-1(z-a_z1)]+ a_ass3b1(x-a_x)1(y-a_y)1(z-a_z2); D_L(x,y,z)=D_L1a[1(x+a_x)-1(x-a_x)][1(y+a_y)-1(y-a_y)][1(z)-1(z-a_z1)]+D_L2a[1(x+a_x)-1(x-a_x)][1(y+a_y)-1(y-a_y)][1(z-a_z2)-1(z-a_z1)]+D_L3a[1(x+a_x)-1(x-a_x)] [1(y+a_y)-1(y-a_y)]1(z-a_z2)+D_L1b1(x-a_x)1(y-a_y)[1(z)-1(z-a_z1)]+D_L2a1(x-a_x)1(y-a_y)[1(z-a_z2)-1(z-a_z1)]+D_L3b1(x-a_x)1(y-a_y)1(z-a_z2) для МС₁ и a_ass(x,y,z)=a_ass1a[1(x+a_x)-1(x-a_x)][1(y+ a_y)-1(y-a_y)][1(z)-1(z-a_z1)]+a_ass2a[1(x+a_x)-1(x-a_x)][1(y+a_y)-1(y-a_y)][1(z-a_z2)-1(z-a_z1)]+ a_ass3a [1(x+a_x)-1(x-a_x)][1(y+a_y)-1(y-a_y)][1(z-a_z3)-1(z-a_z2)]+a_ass4a[1(x+a_x)-1(x-a_x)][1(y+ a_y)-1(y-a_y)][1(z-a_z4)-1(z-a_z3)]+a_ass5a[1(x+a_x)-1(x-a_x)][1(y+a_y)-1(y-a_y)]1(z-a_z4)+a_ass1b 1(x-a_x)1(y-a_y)[1(z)-1(z-a_z1)]+a_ass2b1(x-a_x)1(y-a_y)[1(z-a_z2)-1(z-a_z1)]+a_ass3b1(x-a_x)1(y-a_y) [1(z-a_z3)-1(z-a_z2)]+a_ass4b1(x-a_x)1(y-a_y)[1(z-a_z4)-1(z-a_z3)]+a_ass5b1(x-a_x)1(y-a_y)1(z-a_z3); D_L(x,y,z)=D_L1a[1(x+a_x)-1(x-a_x)][1(y+a_y)-1(y-a_y)][1(z)-1(z-a_z1)]+D_L2a[1(x+a_x)-1(x-a_x)] [1(y+a_y)-1(y-a_y)][1(z-a_z2)-1(z-a_z1)]+D_L3a[1(x+a_x)-1(x-a_x)][1(y+a_y)-1(y-a_y)][1(z-a_z3)-1(z -a_z2)]+D_L4a[1(x+a_x)-1(x-a_x)][1(y+a_y)-1(y-a_y)][1(z-a_z4)-1(z-a_z3)]+D_L5a[1(x+a_x)-1(x-a_x)] [1(y+a_y)-1(y-a_y)]1(z-a_z4)+D_L1b1(x-a_x)1(y-a_y)[1(z)-1(z-a_z1)]+D_L2a1(x-a_x)1(y-a_y)[1(z-a_z2)- 1(z-a_z1)]+D_L3a1(x-a_x)1(y-a_y)[1(z-a_z3)-1(z-a_z2)]+D_L4b1(x-a_x)1(y-a_y)[1(z-a_z4)-1(z-a_z3)]+ D_L5b1(x-a_x)1(y-a_y)1(z-a_z4) для МС₂. Пространственные распределения примеси в ЭС₂ и ЭС₄ для фиксированных моментов времен отжига приведены на рис. 4 и 5.

 

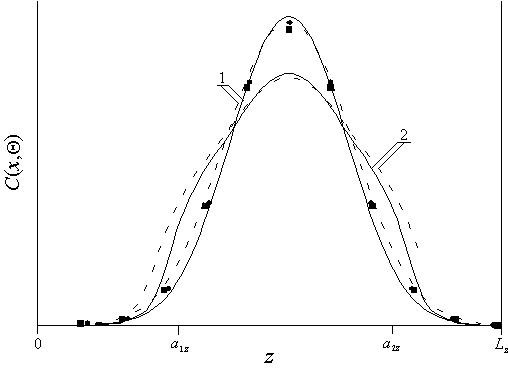
Рис.4. Пространственные распределения имплантированной примеси в однородном материале (кривые 1) и МС₁ (кривые 2) после отжига длительностью Q=0,0075L²/D_0L при D_1L=D_3L<D_2L и D_2L/D_1L=4. Сплошные кривые – аналитический расчет, пунктирные кривые – численный расчет.

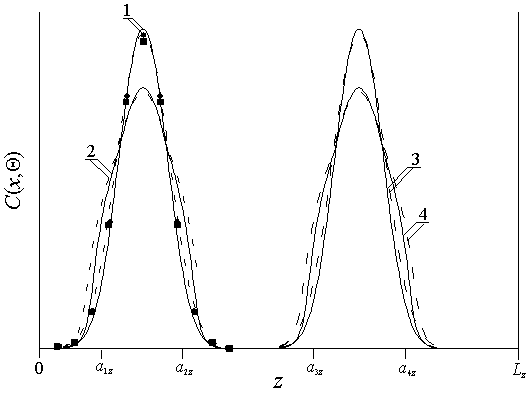
Рис.5. Пространственные распределения имплантированной примеси в однородном материале (кривые 1 и 3) и МС₂ (кривые 2 и 4) после отжига длительностью Q= 0,0075L²/D_0L при D_1L=D_3L=D_5L<D_2L=D_4L и D_2L/D_1L=4. Сплошные кривые – аналитический расчет, пунктирные кривые – численный расчет.

 

Из данных распределений следует, что при условии формирования p-n-перехода в окрестности границы раздела между слоями МС происходит увеличение резкости p-n-перехода (и, как следствие, уменьшение диффузионной составляющей емкости p-n-переходов), а также увеличение равномерности распределения примеси в обогащенной ею области (что, как следствие, позволяет снизить локальные разогревы в процессе работы p-n-перехода или уменьшить глубину его залегания при фиксированном допуске на величину разогрева). По этой причине соотношение между энергиями имплантированных ионов и толщинами эпитаксиальных слоев целесообразно выбирать таким образом, чтобы после окончания отжига радиационных дефектов распределение примеси достигло или почти достигло ближайших к начальному распределению примеси границ раздела между слоями МС. Если по окончании отжига дефектов примесь не достигла необходимых границ раздела представляет интерес дополнительный отжиг примеси. С увеличением длительности отжига увеличивается равномерность распределения примеси в обогащенной ею области с одновременным уменьшением резкости p-n-перехода. Для одновременного наибольшего увеличения резкости p-n-перехода и равномерности распределения примеси в обогащенной ею области необходим выбор компромиссной длительности отжига. В течении отжига с компромиссной длительностью примесь каждого типа должна достигнуть соответствующей границы раздела между слоями МС в направлении z, но глубоко в следующий слой не проникать. Для определения такой длительности воспользуемся введенным в [1-4,12,13] критерием. В рамках данного критерия распределение каждого типа примеси C(x,y,z,t) аппроксимируется скачкообразной функцией заданной ширины (см., например, рис.6).

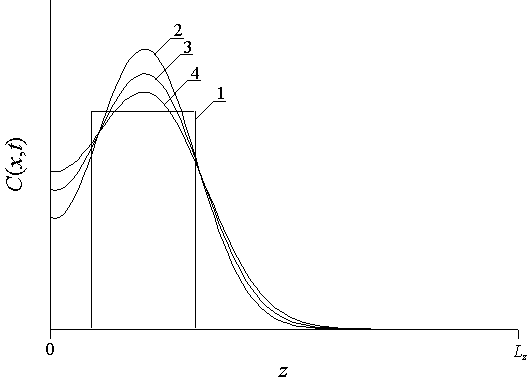
Рис.6. Пространственные распределение в МС_i примеси. Кривая 1 - требуемое идеализированное распределение примеси. Кривые 2-4 – реальные распределения примеси в различные моменты времени (увеличение номера кривой соответствует увеличению длительности отжига).

 

Далее длительность отжига выбирается таким образом, что бы минимизировать среднеквадратичное отклонение аппроксимирующей функции от аппроксимируемой (таким образом, его можно считать также оптимальным). Зависимости оптимального времени отжига от различных параметров приведены на рис.7.

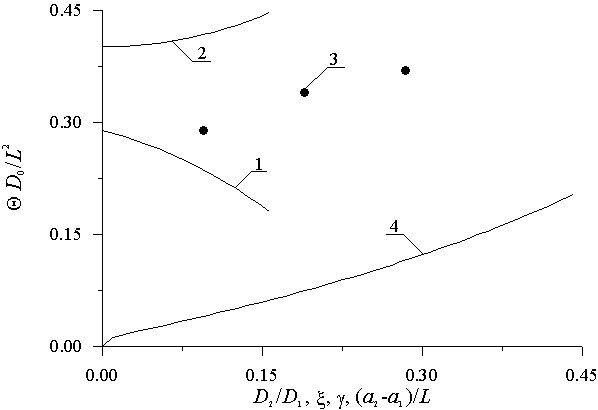
Рис.7. Зависимость безразмерного оптимального времени отжига примеси, полученного из условия минимума среднеквадратического отклонения, от различных параметров МС. Кривая 1 - зависимость времени отжига от отношения D_L2/D_L1, кривые 2 и 3 - зависимости времени отжига от параметров x и g, кривая 4 - зависимость времени отжига от отношения (a_2z-a_1z)/L_z.

 

Для МС₂ значения оптимальных времен отжига в ЭС₂ и ЭС₄ имеют аналогичную друг другу зависимость от параметров. Для того, чтобы компромисс между увеличением резкости p-n-переходов, сформированных в МС₂ на границах ЭС₂ и ЭС₄, и равномерности распределения примеси в обогащенных ею областях был достигнут одновременно для всех p-n-переходов, необходимо выполнение следующих условий: (i) энергия ионов примеси должна быть такой, чтобы центр их распределений находился в серединах соответствующих эпитаксиальных слоев; (ii) параметры МС₂ не могут выбираться независимо друг от друга, а должны удовлетворять следующему соотношению (a_4z-a_3z)²/D₀~(a_2z-a_1z)²/D₀.

Заключение

В данной работе предложен способ уменьшения пространственных размеров системы имплантационных p-n-переходов, входящих в состав транзисторных и тиристорных структур (уменьшение глубины залегания p-n-переходов, а также увеличение степени их интеграции в случае, когда они являются элементами ИС), сформированной в МС, путем выбора свойств данных структур и оптимизации длительности отжига.

 

Данная работа поддержана внутривузовским грантом на научные исследования и иновационную деятельность Нижегородского архитектурно-строительно-го госуниверситета в 2009 г. (приказ № 241) и грантом президента России (проект № МК-548.2010.2).

Приложение

Первое приближение пространственно-временного распределения температуры:

 

 

 

 

.

 

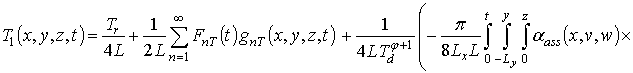
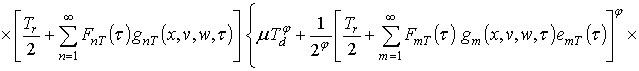
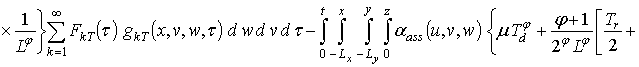
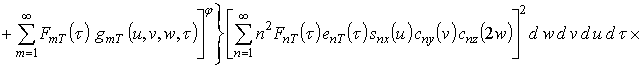
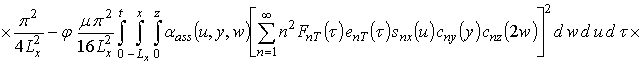
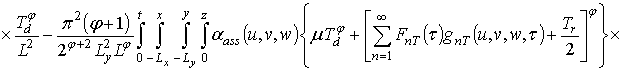
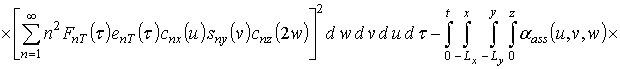
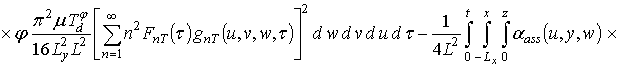
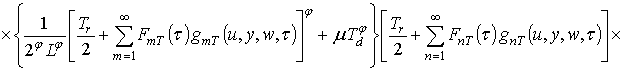
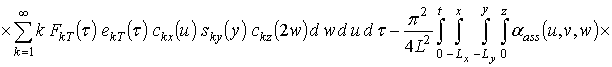
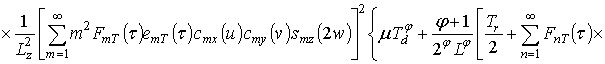
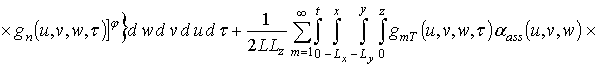
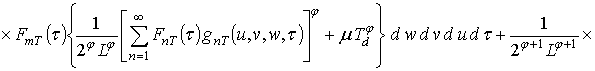
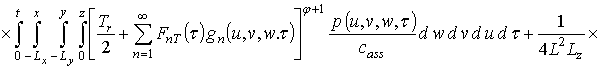
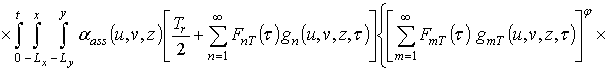
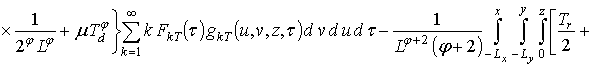
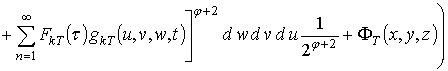Литература

 

[1] E.L. Pankratov // Phys. Rev. B. 2005. V.72, №7. P. 075201-075208.

[2] E.L. Pankratov, B. Spagnolo // The Eur. Phys. J. B. 2005. V.46, №1. P. 15-19.

[3] E.L. Pankratov // Phys. Lett. A. 2008. V.372, №11. P. 1897-1903.

[4] Е.Л. Панкратов. // Журнал радиоэлектроники. 2007. №3. С.9-27.

[5] В.Г. Гусев, Ю.М. Гусев. Электроника. М.: Высшая школа, 1991. 622с.

[6] A.B. Grebene. Bipolar and MOS analogous integrated circuit design. New York, John Wyley and Sons,1983,894p.

[7] З.Ю. Готра. Технология микроэлектронных устройств. - М.: Радио и связь. 1991. 528с.

[8] Y.F. Chong, K.L. Pey, Y.F. Lu, A. T. S. Wee, T. Osipowicz, H. L. Seng, A. See, J.-Y. Dai // Appl. Phys. Lett. 2000. V.77, №19. P.2994.

[9] С.Т. Шишияну, Т.С. Шишияну, С.К. Райлян // ФТП. 2002. Т.36. № 5. С. 611-617.

[10] З.Д. Ковалюк, О.А. Политанская, П.Г. Литовченко, В.Ф. Ластовецкий, О.П. Литовченко, В.К. Дубовой, Л.А. Поливцев // Письма в ЖТФ. 2007. Т.33, №18. С. 14.

[11] J. Park, Y. Huh, H. Hwang, Appl.Phys.Lett. // 1999. V.74, №9. P.1248.

[12] E.L. Pankratov. // J. Phys. D. V.41, №11. P. 115105.

[13] E.L. Pankratov, J.Appl.Phys //. 2008. V.103, №6. P. 064320.

[14] K.K. Ong, K.L. Pey, P.S. Lee, A.T.S. Wee, X.C. Wang, Y.F. Chong // Appl. Phys. Lett. 2006 V.89. № 17. 172111.

[15] E.D. Tsagarakis, C. Lew, M.O. Thompson, E.P. Giannelis // Appl. Phys. Lett. 2006. V.89. № 20. 202910.

[16] В.И. Мажукин, В.В.Носов, U. Semmler // Математическое моделирование. 2000. Т.12. №2. С. 75.

[17] Е.И. Зорин, П.В. Павлов, Д.И. Тетельбаум. Ионное легирование полупроводников. М.: Энергия. 1975. 130 с.

[18] H. Ryssel, I. Ruge. Ion implantation. B.G. Teubner, Stuttgart. 1978. 360 с.

[19] P.M. Fahey, P.B. Griffin, J.D. Plummer // Rev. Mod. Phys. 1989. V.61. № 2. P. 289-388.

[20] К.В. Шалимова. Физика полупроводников. М.:Энергоатомиздат, 1985. 391 с.

[21] Ю.Д. Соколов // Прикладная Механика. 1955. Т.1, С. 23-35.

[22] E.L. Pankratov // The Eur. Phys. J. B. 2007. V.57, №3. P. 251-256.