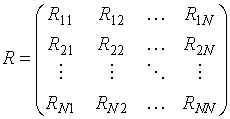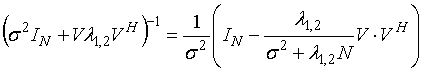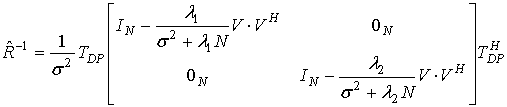УДК 621.317:621.391

 

Поляриметрическая обработка РАДИОЛОКАЦИОННЫХ данных

 

Р. Н. Акиншин ¹, А. В. Хомяков ² А. А. Бортников ³

 

¹ Секция прикладных проблем при Президиуме РАН, г. Москва

² ОАО Центральное конструкторское бюро аппаратостроения, г. Тула

³ Тульский государственный университет

 

Получена 30 мая 2011 г.

 

Аннотация. Рассмотрена поляриметрическая обработка массивов данных антенной решеткой, дающая значительный выигрыш в обнаружении. Предложен эффективный алгоритм, инвертирующий корреляционную матрицу мешающих отражений, который может быть частью адаптивного процессора антенной решетки. Проведено моделирование на базе минимальной средней квадратичной ошибки, показавшее эффективность поляриметрической адаптивной обработки.

Ключевые слова: антенная решетка,  матрица когерентности,  поляриметрический канал, алгоритм, адаптивный процессор.

Abstract. The polarimetric processing of data array which gives a significant gain in detection is considered. An efficient algorithm for inverting the correlation matrix of clutter, which may be part of an adaptive antenna array processor is suggested. The simulation based on the minimum mean squared error, which showed the effectiveness of polarimetric adaptive processing is carried out.

Keywords: antenna array, matrix of coherence, polarimetric channel, algorithm, adaptive processor.

 

Адаптивная обработка массивов данных антенной решеткой открывает новые возможности в подавлении мешающих отражений и гибкий сценарий сканирования диаграммы направленности антенны. Дополнительные возможности достигаются использованием поляриметрической информации о цели. Обычная обработка массивов данных антенной решеткой не пригодна в ситуациях, когда направления цели и мешающих отражений совпадают. Преимущество поляриметрической обработки в том, что цель может быть обнаружена даже в сложной помеховой обстановке, обеспечивая разницу поляриметрических свойств мешающих отражений и цели.

Рассмотрим линейную антенную решетку с N поляриметрическими элементами. Во избежание дифракционных максимумов решетки, расстояние d между смежными парами диполей ≤l/2, где l-длина волны. Для и , являющихся, соответственно, выходными временными сигналами осей x и y n-ого диполя, выходной вектор ортогонального диполя  будет иметь вид:

.

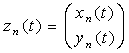Запись n выходных векторов в вектор-столбец с 2N элементами:

,

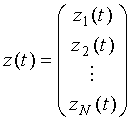определяет временную выборку антенной решетки [1]. Полная корреляционная матрица имеет вид:

,

где  обозначает математические ожидания, а  - сопряженный перенос. Оценка максимального подобия  для R рассчитывается по формуле:

,

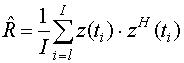с использованием I имеющихся временных выборок измеренных или экспериментальных данных.

Деление R на 2*2 субматрицы:

 

,                                          (1)

удобно потому, что расчлененные R_nm представляют корреляцию между элементами кросс диполя, обозначенными n и m c учетом разностей фаз, являющихся результатом их местонахождения.

Обычно, использующиеся описание поляризованных электромагнитных волн основано на комплексном векторе амплитуды , где  и - векторы (амплитуды и фазы) ортогональных компонентов электрического поля. Временной сигнал в n-ом диполе, принимающем детерминированный источник c частотой  и начальной фазой , может быть записан как:

,

где:

,

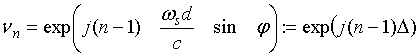описывает относительную разность фаз между n-ым элементом антенны и первым элементом.  - угол падения сигнала в плоскости xz, с – скорость света. Используя эти определения, запишем корреляционную матрицу на выходе элемента  и :

.                         (2)

Для групповой цели с K детерминированными сигналами выражение расширится:

,

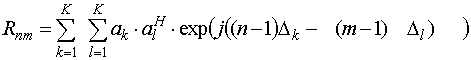где индексы k и l соответствуют определенным источникам. Комбинация этих субматриц в соответствии с (1) дает корреляционную матрицу R для всей линейной антенной решетки.

Субматрица, соответствующая (2) представляет корреляционную матрицу, применительно к ситуации с одной целью. Член  часто называют матрицей когерентного сигнала [2]. Все субматрицы состоят из этой матрицы, определенной членом фазы . При определении управляющего вектора:

,

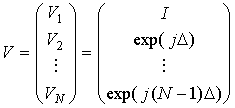корреляционная матрица может быть записана в форме:

,

где  означает произведения Кронекера.

Одним из компонентов сигнала, присутствующем всегда в измеренных данных является шум. Допускаем, что он некоррелирован от элемента к элементу и имеет гауссово распределение с нулевым математическим ожиданием. Если мы  допускаем равную мощность шума во всех 2N выходных сигналах, влияние  на корреляционную матрицу будет просто , где  обозначает матрицу размера 2N. Таким образом, имеем корреляционную матрицу измеренных данных:

,                                             (3)

где s ²-дисперсия шума.

Матрица когерентности сигнала J играет центральную роль в описании корреляционной матрицы антенной решетки. При анализе обстановки с мешающими отражениями, ее просто заменяют на матрицу когерентности мешающих отражений J_c в (3). Для данного случая нет необходимости знать точную форму J_c.

Важным шагом обработки является разделение ортогональных поляриметрических каналов. Это достигается путем диагонализации субматриц  в , с использованием разложения собственного значения. Любая субматрица может быть записана в форме:

,

где D – диагональная матрица собственных значений:

,

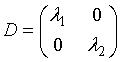а столбцы М – соответствующие собственные векторы. Диагонализация всех субматриц приводит к выражению:

Нет необходимости в расчете собственного разложения всех субматриц. Поскольку мы определили М путем разложения любой , его можно использовать для преобразования всех субматриц в соответствии с:

.

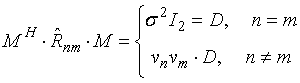Матрица , состоящая из 2*2 субматриц в диагональной форме, теперь комбинируется как блочная матрица в соответствии с:

,

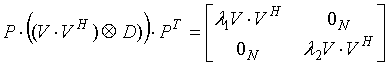 означает квадратичную нулевую матрицу размера N. Перестановочная матрица P должна иметь вид:

.

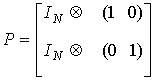Для N=3:

.

После этих линейных операций, модифицирующих измеренную корреляционную матрицу, представляем корреляционную матрицу как:

,

.                          (4)

Используем правило инверсии [3]:

и рассчитывая , , U=V  и V=V^H получим:

,                          (5)

для инверсий не нулевых блочных матриц в (4) с 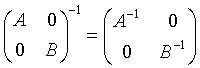 и  инверсия корреляционной матрицы может быть выражена:

.            (6)

Для рассматриваемого случая необходимо выразить уравнение (6) в членах R. Сравнение (4) и (6) показывает идентичные члены . Выражая (4) в этих членах:

,

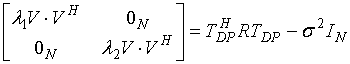и подставляя его в (5) получаем, после элементарных преобразований:

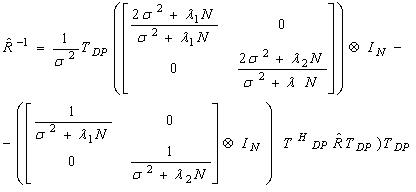 .                           (7)

Собственные значения  и мощность шума  по-прежнему неизвестны и должны быть получены из измеренной корреляционной матрицы . Любая диагонализированная  характеризует элементы (7):

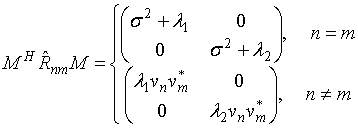.                                  (8)

Поскольку собственные значения  всегда являются положительными, реальными числами, а , они должны быть рассчитаны путем формирования абсолютных значений элементов в (8). Извлекая  или  из (8) получаем необходимое . Полученные таким образом значения  и  должны рассматриваться как оценки, что обусловлено ограниченным числом выборок, из которых рассчитывалось корреляционная матрица. Для подавления влияния изменений формируются усредненные матрицы, перед решением для  и . Арифметическое усреднение возможно для всех  с идентичными членами фазы . Тогда соответствующей матрицей для получения  будет:

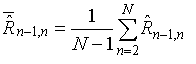,                                          (9)

в то время, как усреднение основных диагональных субматриц:

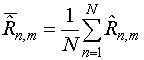,                                             (10)

обеспечивает лучшую оценку . Одна из матриц (9), (10) может быть разложена по собственному значению, решая матрицу преобразования М, необходимую для инициирующей диагонализации.

Итак, представлены все детали для закрытой инверсии измеренной корреляционной матрицы мешающих отражений, при условии, что помеховая обстановка характеризуется одним доминантным направлением.

Некоторые методы обработки адаптивной антенной решеткой предполагают инверсию корреляционной матрицы мешающих отражений для установки весовых коэффициентов. В поляриметрической антенной решетке каждый элемент n нуждается в отдельном весовом значении , для ортогональных сигналов. Выходной сигнал процессора имеет вид:

,                                               (11)

где z – комбинированные сигналы антенны, как обозначено в (2), а w – эквивалентно сформированный вектор весовых коэффициентов. В зависимости от используемой меры рабочие характеристики (среднеквадратичная ошибка, максимальное подобие – ML и т.п.), весовые значения рассчитываются из [4]. Для минимальной s  отношение имеет вид:

,                                                 (12)

что дает оптимальные весовые значения для нужного направления , выражением, контролирующим вектором V_Z, который определяется как:

.                                                                      

Моделирование обработки мешающих отражений нуждается в статистической модели сигнала для выработки входных данных. Источник сигнала должен сформировать векторную временную последовательность  для обеих ортогональных поляризаций. Корреляционная матрица последовательности должна быть идентична данной матрице когерентности мешающих отражений J_c.

Это может быть достигнуто преобразованием комплексных, гауссово распределенных двух случайных величин вероятностного процесса , сформированного компьютером:

.

Линейное преобразование матрицы T вновь основывается на разложении собственного значения матрицы когерентности:

Легко заметить, используя:

,

что ожидание с(t) приводит к J_c, корреляционная матрица вероятностного процесса n(t) равна единице.

Допустим, что сигнал мешающих отражений является стохастической не полностью поляризованной плоской волной с вектором поляризации p и степенью поляризации p. Эти параметры также описывают матрицу когерентности мешающих отражений [2]. Процесс мешающих отражений имеет для моделирования левостороннюю круговую поляризацию  с p=0.8.

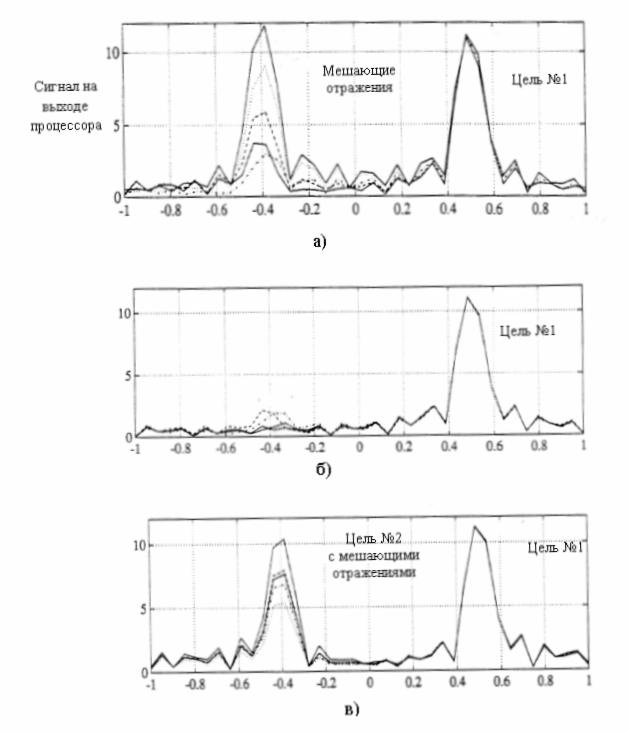
Рис. 1. - Результаты обработки сигнала.

 

На рисунке 1а показаны результаты обработки сигнала на выходе линейной антенной решетки с N=16 элементами, принимающей сигнал детерминированного источника с направлением  мощности  и сигнал источника мешающих отражений с направлением  мощности  без адаптации . Для каждого направления  соответствующий весовой коэффициент V_z должен формироваться на выходе процессора |s(t)|, по формуле (11). Число направлений равно 40.

Оценим и инвертируем корреляционную матрицу мешающих отражений для расчета W_s (12) при отсутствии цели, осуществляя адаптивное подавление мешающих отражений, (см. рисунок 1б). Отбеливающий эффект пространственного узкополосного режекторного фильтра, представленный коэффициентами фильтра W_xn, W_yn, очевиден. Однако, как показывает рисунок 1в, характеристика фильтра поляриметрически чувствительна. Если возникает вторая цель с тем же направлением, что и мешающие отражения и с той же мощностью, что и цель №1, то она легко обнаруживается, благодаря своей противоположной поляризации – правосторонней, круговой .

При моделировании описанной обработки, степень свободы существует в дисперсии шума от .

Изменение главных диагональных элементов корреляционной матрицы моделированных мешающих отражений дает выбор между лучшим подавлением мешающих отражений или лучшим обнаружением цели в условиях мешающих отражений. Это следует принимать в расчет при практических действиях.

Таким образом, обработка поляриметрической антенной решеткой массива данных дает значительный выигрыш в обнаружении. Предложен эффективный алгоритм, инвертирующий корреляционную матрицу мешающих отражений, используя ее особую структуру в ситуациях с одним источником отражения. Этот алгоритм может быть частью адаптивного процессора антенной решетки. Было проведено моделирование на базе минимальной средней квадратичной ошибки s, показавшее эффективность поляриметрической адаптивной обработки. Аналогичные расчеты можно проделать для полностью поляриметрических радиолокационных станций.

 

Литература

1. J. Li, R.T. Compton Jr.: «Angle and Polarization Estimation Using ESPRIT with a Polarization Sensitive Array»; IEEE Transaction on Antennas and Propagation, vol. 39, no. 9, pp. 1376-1383, Sept. 1991.

2. G. Wanielik: Signaturuntersuchungen an einem polarimetrischen Pulsradar, Fortschr. –Ber. VDI Reihe 10,  Nr. 97; VDI – Verlag,  Dusseldorf, 1988.

3. G.A.F. Seber: Multivariate Observations; John Wiley & Sons, Inc., 1984.

4. R. Monzingo, T. Miller: Introduction to Adaptive Arrays; John Wiley & Sons, Inc., 1980.