ВЛИЯНИЕ ФАЗОВОГО СДВИГА ИМПУЛЬСОВ ДВИГАТЕЛЬНЫХ ЕДИНИЦ НА СТРУКТУРУ СПЕКТРА ЭЛЕКТРОМИОСИГНАЛА
А. М. Шайдук, С. А. Останин
ГОУ ВПО «Алтайский государственный университет», г. Барнаул
Получена 27 мая 2011 г.
Аннотация. Проанализирована структура спектра электромиографического сигнала, представляющего собой сумму сдвинутых относительно друг друга по фазе периодически следующих импульсов. Аналитически установлена связь между статистическими свойствами случайной разности фаз и видом спектра мощности сигнала. Приведены результаты численного эксперимента.
Ключевые слова: спектральный анализ хаотических сигналов, математическое моделирование.
Abstract. The structure of the spectrum of the
electromyographic signal is the sum of shifted relative to each other on stage
from time to time following the pulse. The connection between the
statistical properties of the random phase difference and a view of the power
spectrum of the signal is found analytically. Results of numerical experiment
are given.
Key words: spectral analysis of random signals, mathematical modeling.
Спектральные методы являются эффективным средством анализа периодических сигналов. Существуют такие сигналы, например интерференционные электромиограммы, которые изменяются во времени хаотически, хотя представляют собой аддитивную смесь периодических или квазипериодических последовательностей моноимпульсов электрического потенциала действия мышечных структур (двигательных единиц). С точки зрения диагностики состояния нервно-мышечной системы, интерес представляет проблема оценки статистических характеристик параметров таких последовательностей по спектру. Целью данной работы было установление влияния фазового сдвига импульсов двигательных единиц на структуру спектра электромиосигнала.
Пусть зависимость
напряжения от времени для потенциала отдельной двигательной единицы (ПДОДЕ)
есть функция ![]() .
Вид этой функции обычно устанавливается экспериментально инвазивными методами. Электромиографический
сигнал одной двигательной единицы
.
Вид этой функции обычно устанавливается экспериментально инвазивными методами. Электромиографический
сигнал одной двигательной единицы ![]() , снимаемый накожным методом, представляет
собой сумму отдельных потенциалов действия, сдвинутыми друг относительно друга
на время
, снимаемый накожным методом, представляет
собой сумму отдельных потенциалов действия, сдвинутыми друг относительно друга
на время ![]()
где ![]() – полное число отдельных импульсов ПДОДЕ,
генерируемое за время регистрации электромиограммы.
– полное число отдельных импульсов ПДОДЕ,
генерируемое за время регистрации электромиограммы.
При измерении накожным
методом регистрируемый сигнал создается обычно не одной двигательной единицей.
Двигательные единицы, расположенные рядом с электродами, создают на последних
некоторое напряжение такого же типа, как и сигнал (1), поскольку управляются
одним нервным волокном. Однако, в силу различных причин, полный регистрируемый
сигнал будет являться суперпозицией сигналов типа (1), случайно сдвинутых относительно
друг друга по оси времени на некоторую величину ![]() , где индекс
, где индекс ![]() есть условный номер двигательной единицы.
есть условный номер двигательной единицы.
В случае одинакового
вклада некоторого количества ![]() двигательных единиц, регистрируемый сигнал
принимает вид
двигательных единиц, регистрируемый сигнал
принимает вид
В [2] показано, что из
свойств преобразования Фурье следует мультипликативность спектра сигнала,
генерируемого одной двигательной единицей. В [3] показано, что и в случае
сигнала типа (2), в котором учитывает генерация сигналов многими двигательными
единицами, мультипликативность спектра сохраняется и добавляется новый
сомножитель, описывающий влияние интерференции сигналов от множества
двигательных единиц. Комплексная спектральная функция ![]() сигнала (2) есть
сигнала (2) есть
![]() (3)
(3)
где
 , (4)
, (4)
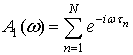 , (5)
, (5)
 . (6)
. (6)
Измеряемая обычно спектральная
мощность сигнала ![]() является
вещественной функцией и определяется как
является
вещественной функцией и определяется как
![]() . (7)
. (7)
Рассмотрим здесь, как влияет на
наблюдаемый спектр случайный сдвиг фаз между различными двигательными
единицами. Это влияние целиком описывается функцией ![]() .
.
Для вычисления выражения (6)
необходимо знать явный вид последовательности ![]() . Поскольку эта последовательность
формируется случайно, необходимо определить тип статистики, которой подчиняется
величина
. Поскольку эта последовательность
формируется случайно, необходимо определить тип статистики, которой подчиняется
величина ![]() .
.
Вероятность ![]() получить значение
получить значение ![]() в интервале
в интервале ![]() определяется плотностью
вероятности
определяется плотностью
вероятности ![]() :
: ![]() Если требуется вычислить спектральную функцию (6) одной
реализации, необходимо задать плотность вероятности
Если требуется вычислить спектральную функцию (6) одной
реализации, необходимо задать плотность вероятности ![]() и провести численное
моделирование суммы (6), используя соответствующий генератор случайных чисел.
и провести численное
моделирование суммы (6), используя соответствующий генератор случайных чисел.
На рисунке 1 приведен
результат моделирования компоненты спектра мощности ![]() для равномерного распределения
величины
для равномерного распределения
величины ![]() на
отрезке
на
отрезке ![]() , т.е
плотность вероятности
, т.е
плотность вероятности
 (8)
(8)
Из рисунка 1 видно, что на частоте ![]() функция
функция ![]() обращается в ноль. Это
приведет к возникновению характерного провала в полном спектре
обращается в ноль. Это
приведет к возникновению характерного провала в полном спектре ![]() электромиосигнала.
Заметим, однако, что этот результат справедлив для конкретной реализации.
электромиосигнала.
Заметим, однако, что этот результат справедлив для конкретной реализации.
На рисунке 2 приведен
результат численного моделирования ![]() для гауссовского распределения плотности
вероятности
для гауссовского распределения плотности
вероятности ![]() со
стандартным отклонением
со
стандартным отклонением ![]() , т.е.
, т.е.
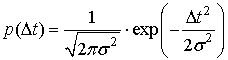 . (9)
. (9)
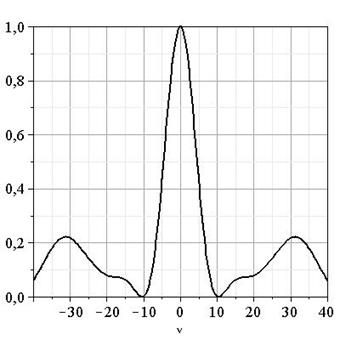
Рис. 1. Реализация спектральной плотности ![]() , обусловленной случайным сдвигом фаз.
Равномерное распределение
, обусловленной случайным сдвигом фаз.
Равномерное распределение ![]() , число двигательных единиц
, число двигательных единиц ![]() .
.
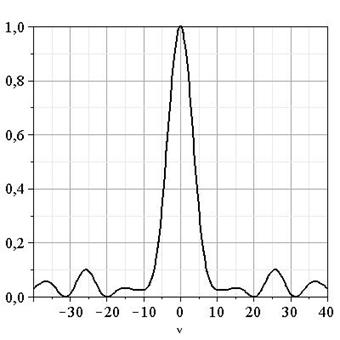
Рис. 2. Реализация спектральной плотности ![]() , обусловленной случайным сдвигом фаз.
Гауссовское распределение со стандартным отклонением
, обусловленной случайным сдвигом фаз.
Гауссовское распределение со стандартным отклонением ![]() , число двигательных единиц
, число двигательных единиц ![]() .
.
В этой реализации на частоте ![]() в полном спектре
в полном спектре ![]() минимума наблюдаться не
будет, но появляются минимумы на приблизительно удвоенной частоте.
минимума наблюдаться не
будет, но появляются минимумы на приблизительно удвоенной частоте.
Вычислим теперь спектр
мощности ![]() усредненный
по бесконечному числу реализаций:
усредненный
по бесконечному числу реализаций:
 . (10)
. (10)
Выражение (10)
представляет собой среднее от суммы ![]() слагаемых типа
слагаемых типа ![]() . Среднее от суммы равно сумме
средних, поэтому достаточно найти среднее слагаемого
. Среднее от суммы равно сумме
средних, поэтому достаточно найти среднее слагаемого ![]() .
.
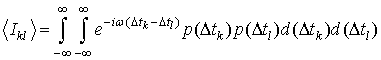 . (11)
. (11)
При ![]() в силу нормировки плотности вероятности
в силу нормировки плотности вероятности ![]() . Если
. Если ![]() , то
, то
![]() (12)
(12)
где
 (13)
(13)
спектральная функция плотности
вероятности распределения величины ![]() .
.
Таким образом, спектр
мощности ![]() полностью
определяется спектром мощности плотности вероятности
полностью
определяется спектром мощности плотности вероятности ![]() . Теперь, выполняя суммирование в
(10) с учетом (12), получаем окончательно
. Теперь, выполняя суммирование в
(10) с учетом (12), получаем окончательно
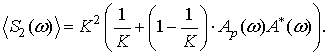 (14)
(14)
Для получения количественных оценок необходимо использовать какой-либо явный тип плотности вероятности. Пусть, например, используется равномерное распределение (8). В этом случае

и средний по реализациям спектр
мощности ![]() есть
есть
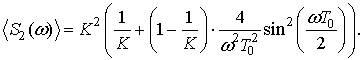 (15)
(15)
На рисунке 3 приведен
нормированный на ![]() спектр
мощности
спектр
мощности ![]() для
равномерного распределения величины случайного сдвига фаз. Теперь этот
сомножитель
для
равномерного распределения величины случайного сдвига фаз. Теперь этот
сомножитель ![]() не
обращается в ноль и спектральные линии в спектре полного миосигнала исчезнуть
не могут. Будут наблюдаться характерные провалы на нескольких первых частотах
не
обращается в ноль и спектральные линии в спектре полного миосигнала исчезнуть
не могут. Будут наблюдаться характерные провалы на нескольких первых частотах ![]() ,
, ![]() . Минимальное значение
сомножителя
. Минимальное значение
сомножителя ![]() есть
есть
![]() , т.е.
спектральная мощность полного сигнала просто пропорциональна числу участвующих
в его формировании двигательных единиц. Интерференционные эффекты наблюдаются
лишь в диапазоне частот вблизи нуля
, т.е.
спектральная мощность полного сигнала просто пропорциональна числу участвующих
в его формировании двигательных единиц. Интерференционные эффекты наблюдаются
лишь в диапазоне частот вблизи нуля ![]()
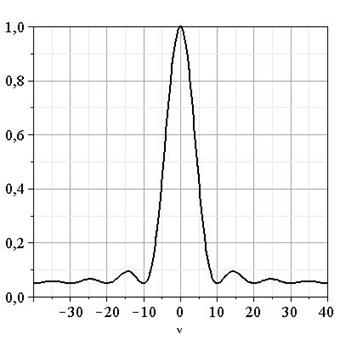
Рис. 3.
Средний спектр мощности ![]() , обусловленный случайным сдвигом фаз.
Равномерное распределение
, обусловленный случайным сдвигом фаз.
Равномерное распределение ![]() , число двигательных единиц
, число двигательных единиц ![]() .
.
Если случайный сдвиг фаз
подчиняется нормальному распределению типа (9) со стандартным отклонением ![]() , то
, то
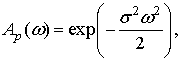
и усреднение по реализациям дает
 (16)
(16)
Этот спектр мощности (нормированный
на ![]() ) приведен
на рисунке 4.
) приведен
на рисунке 4.
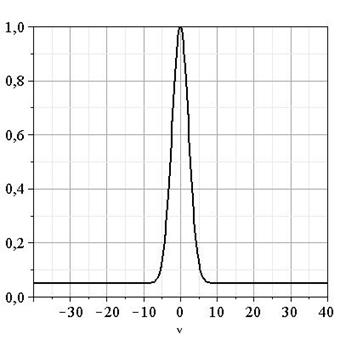
Рис. 4. Средний спектр мощности ![]() , обусловленный случайным сдвигом фаз.
Гауссовское распределение со стандартным отклонением
, обусловленный случайным сдвигом фаз.
Гауссовское распределение со стандартным отклонением ![]() , число
двигательных единиц
, число
двигательных единиц ![]() .
.
При таком типе статистики
усреднение по реализациям приводит к исчезновению характерных «провалов» в
полном спектре мощности, хотя в отдельных реализациях они могут появляться.
Интерференционные эффекты от сложения сигналов от разных двигательных единиц в
спектре проявляются лишь в диапазоне частот близи нуля. Диапазон частот
определяется стандартным отклонением ![]() . Если величина
дисперсии сравнима с характерным периодом следования импульсов в одной
двигательной единице, то интерференционные эффекты могут совсем не проявляться
в усредненном по реализациям полном спектре мощности. Спектральная мощность
сигнала в этом случае практически на всех частотах будет пропорциональна
количеству участвующих в его формировании двигательных единиц.
. Если величина
дисперсии сравнима с характерным периодом следования импульсов в одной
двигательной единице, то интерференционные эффекты могут совсем не проявляться
в усредненном по реализациям полном спектре мощности. Спектральная мощность
сигнала в этом случае практически на всех частотах будет пропорциональна
количеству участвующих в его формировании двигательных единиц.
Литература
1. Физиология человека / Под ред. Г.И. Косицкого. – М.: Медицина, 1985. – 544 с.
2. Рангайян Р.М. Анализ биомедицинских сигналов. Практический подход / Пер. с англ. под ред. А.П. Немирко. – М.: ФИЗМАТЛИТ. – 2007. – 440 с.
3. Шайдук А.М., Останин С.А. Моделирование электромиографического сигнала средствами LabVIEW. Известия Алтайского государственного университета. – Барнаул: Изд.-во АлтГУ – Ч.1(65), 2010. – С. 195 – 201.
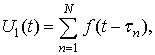 (1)
(1)