УДК 621.317.08; 621.317.1; 621.317.6

 

СПОСОБ ЛИНЕАРИЗАЦИИ РАНГОВЫХ ХАРАКТЕРИСТИК ИДЕНТИФИКАЦИОННЫХ ШКАЛ

 

А. А. Горшенков,   Ю. Н. Кликушин

Омский государственный технический университет

 

Получена 23 мая 2011 г.,  после доработки – 7 июня 2011 г.

 

Аннотация. Предложен способ линеаризации ранговых характеристик идентификационных шкал. Описан пример применения данного способа для обнаружения и визуализации неоднородности структуры идентификационных шкал. Показаны классификационные возможности способа.

Ключевые слова: аналитические модели, идентификационные шкалы распределений, линеаризация, структурные неоднородности.

Abstract. A method of linearization of rank identification performance scales was described. We describe an example application of this method for the detection and visualization of structure inhomogeneity identity scales. The classification possible way was shown.

Keywords: analytical models, identification of the scale distribution, linearization, structural heterogeneity.

 

ВВЕДЕНИЕ

Познавательной основой современной теории измерений является теория шкал [1,2], которая утверждает, что любое свойство объекта или процесса может быть измерено, т.е. отображено в некоторый числовой эквивалент. Принадлежность этих чисел к номинальной, порядковой, интервальной, масштабной или натуральной шкалам  определяется свойствами чисел. Иерархия шкал (от номинальной до натуральной) соответствует последовательности уровней и этапов познания объекта исследования. Чем глубже изучено некоторое свойство, тем более высокий статус имеет числовая шкала и тем больше информационных и вычислительных процедур можно применять к этим числам. В частности, если некоторое свойство может быть отображено только суждениями «да – нет» и, соответственно, записано в виде двух чисел (1 и 0), то можно говорить о  самых простых измерениях, реализуемых в рамках номинальной шкалы.  Интересно, что, хотя в номинальной шкале допускается статистическая обработка, но только в отношении оценки частости и модальности. А вот оценивать такой статистический параметр, как матожидание  – уже нельзя, поскольку, например,  среднее значение от 1 и 0 дает значение 0,5, которого в этой шкале нет.

Второй по значимости, после номинальной, является порядковая шкала, в которой интенсивность проявления какого-либо свойства может быть упорядочена и выражена в порядковых номерах (рангах). Идентификационными будем называть такие шкалы (ИШ), которые с помощью числовых показателей упорядочивают лингвистические характеристики, например, имена, объектов или процессов. Примеры ИШ представлены в табл. 1.

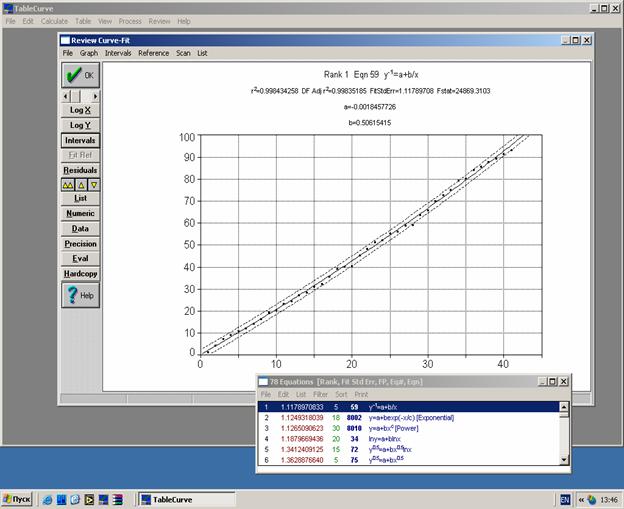
Самой известной ИШ является периодическая система химических элементов Д.И. Менделеева, традиционную и другие формы представления которой можно найти на сайте [3]. Если в качестве упорядочивающих числовых коэффициентов принять, как и первоначально предлагал сам Д.И. Менделеев, атомный вес элементов, то получим функциональную зависимость (рис. 1) - ИШ, связывающую порядковый номер (ранг) элемента и его атомный вес. Таким образом, в таблице Д.И. Менделеева на логическом уровне (в виде порядковых номеров) происходит связывание количественных оценок (атомных весов) с качественными состояниями объектов, в данном случае химических элементов.

Поскольку атомный вес элемента является измеримой величиной, то данная идентификационная шкала относится к классу объективных шкал. Другим примером порядковой ИШ служит международная температурная шкала (МТШ-90), которая является практической основой  всех  теплофизических измерений [4].

Таблица 1

Примеры идентификационных шкал

№ п/п	Вид ИШ	Элементы кортежа			Примечание
		Имя	Ранг	Значение
1	Таблица химических элементов Д.И. Менделеева	Наименование химического элемента	Порядковый номер химического элемента	Атомный вес	Измеримые величины
2	Цветовые шкалы	Наименование цвета	Порядковый номер цвета: 1-красный; 2-зеленый; 3-голубой	Длина волны излучения	Измеримые величины
3	Шкалы твердости (абсолютные)	-	Баллы по шкалам Мооса, Роквелла	Глубина и сила вдавливания в поверхность материала эталонного объекта	Измеримые величины
4	Шкалы твердости (относительные)	-	Порядковый номер относительно номера алмаза	Наличие или отсутствие царапин на поверхности материала	Неизмеримые величины
5	Шкалы ураганов, землетрясений		Баллы по шкале Рихтера	Скорость и сила ветра	Измеримые величины
6	Шкала оценки качества знаний	-	Баллы	Субъективные качественные оценки (неудовлетворительно, удовлетворительно, хорошо, отлично)	Неизмеримые величины
7	Список сотрудников	Фамилии сотрудников	Порядковый номер ФИО в списке по алфавиту	-	Неизмеримые величины
8	Список сотрудников	Фамилии сотрудников	Порядковый номер ФИО в списке по росту	Рост	Измеримые величины
9	Шкала распределений мгновенных значений сигналов	Название распределения	Порядковый номер распределения	Идентификационное число	Измеримые величины
10	Международная температурная шкала (МТШ-90)	Наименование реперной точки	Порядковый номер реперной точки	Температура реперной точки	Измеримые величины

 

Аналитическая форма записи для периодической системы в простейшем виде представляет собой прямую линию [5]:

,                                                      (1)

где: Х – порядковый номер элемента, Y – атомный вес, А≈0 и В=2,5350877 – константы. Погрешность подобной аппроксимации, максимальна в середине таблицы (N=57, элемент <Лантан>, атомный вес = 138,9) и не превышает 4%. При решении задач научной классификации и предсказания положения и свойств еще неизвестных химических элементов, такая погрешность является допустимой.

Таким образом, периодическая система химических элементов является объективной, линейной ИШ. Линейность ранговой характеристики периодической системы имеет глубокий физический смысл, поскольку именно ранг определяет количество протонов в ядре атома химического элемента.

 

 

Рис. 1. Идентификационная шкала периодической системы химических элементов Д.И. Менделеева.

 

ИШ являются чисто эмпирическими объектами, которые не могут (по крайней мере, на данном уровне познания) быть сформированы, исходя из теоретических соображений. Поэтому линейность ИШ является скорее исключением, чем правилом. Так, например, все ИШ распределений вероятности, описанные в монографиях [6-8], представляют собой нелинейные объекты.

Нелинейность ранговых характеристик ИШ вызвана неравномерным распределением значений реперных точек на числовой оси. Эта неравномерность скрывает действительную закономерность расположения эталонов. Поэтому (в отличие от периодической системы химических элементов) не представляется возможным понять, какой физический смысл имеют порядковые номера в этих типах ИШ.

Целью данной работы является поиск скрытых закономерностей расположения реперных точек ИШ. Указанная цель достигается путем линеаризации ранговых характеристик с пересчетом порядковых номеров эталонов.

 

МЕТОДИКА И ИНСТРУМЕНТЫ ИССЛЕДОВАНИЯ

Идея предлагаемого способа линеаризации поясняется на примере ИШ, реализованной в структуре, так называемого, FRaSH-тестера [9]. Элементами восьми кортежей этого тестера (табл. 2) являются имена распределений вероятности случайных сигналов (2mod – двумодального, asin – арксинусного, even – равномерного, trap – трапецеидального, simp – треугольного, gaus – нормального, lapl – двустороннего экспоненциального, kosh – Коши), их ранги (Rank) и значения (A_frm) параметра формы.

Таблица 2

Идентификационная шкала FRaSH-тестера

N=10000, L=100	Вид распределения случайного сигнала
	2mod	asin	even	trap	simp	gaus	lapl	kosh
Rank	1	2	3	4	5	6	7	8
Afrm	4	6,28	8	10	12	19	36	3000

 

Способ линеаризации ИШ состоит из нескольких этапов.

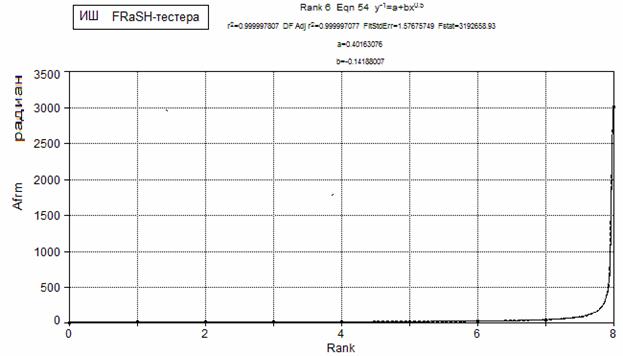
Во-первых, подбираем для ранговой характеристики (табл. 2) аналитическую модель (рис. 2). Поскольку процедура подбора моделей в соответствующих программных средах (например, TCWin) носит оптимизационный характер, то практически всегда можно найти компромисс между сложностью ранговой модели и ее погрешностью. Для ИШ (табл. 2) уравнение модели имеет вид:

 ,                                                            (2)

где: Y = A_frm – параметр формы, радиан; X = Rank – ранг; A≈0,402; B≈-0,142 – коэффициенты модели.

 

Рис. 2. Ранговая характеристика ИШ FRaSH-тестера.

 

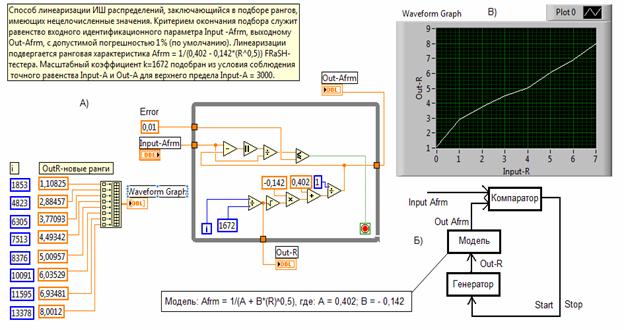
Второй этап заключается в линеаризации аналитической характеристики (2). Рассматриваемый способ линеаризации ИШ состоит в уравновешивании измеряемых значений идентификационного параметра (Input Y) нелинейно изменяющимся во времени сигналом виртуального параметра (Out Y).  Нелинейная развертка реализуется за счет использования ждущего линейного генератора и нелинейной модели, построенной по соотношению (2). Запуск и останов ждущего генератора осуществляется выходным сигналом компаратора  (рис. 3,Б). В момент сравнения выполняется равенство: OutA_frm = InputA_frm с точностью до погрешности компаратора, которая по умолчанию установлена на уровне 1%. Выходной величиной линеаризатора являются значения рангов (Out-R), определяемые с учетом масштабного коэффициента (k) по формуле:

.                                                      (3)

Значения масштабного коэффициента подбирается с учетом обеспечения минимальной погрешности аппроксимации на верхнем пределе измерения идентификационного параметра (maxA_frm =3000, табл. 2).

 

 

Рис. 3. Иллюстрации способа линеаризации ИШ FRaSH-тестера.

 

 

 

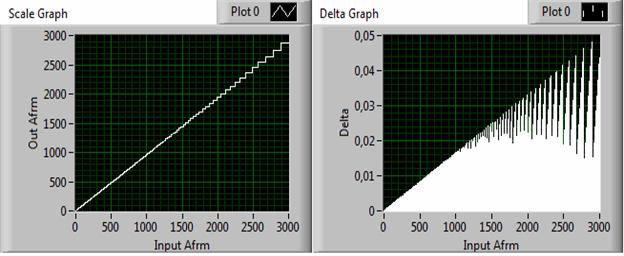
Рис. 4. Статическая характеристика ИШ (Scale Graph) и погрешность аппроксимации (Delta Graph).

 

Линеаризацию шкалы можно представить в виде соответствующей структурной схемы и реализовать ее в виде виртуальной модели, например, в среде LabVIEW (рис. 3,А). В качестве иллюстрации, на рис. 3 показаны:  также структура линеаризатора (рис. 3, Б) и график, связывающий исходные и приведенные выходные ранги (рис.3,В).

На рис. 4 представлено два графика (Scale Graph) и (Delta Graph): первый подтверждает линейность новой ИШ FRaSH-тестера, а второй показывает, как распределена погрешность аппроксимации по длине шкалы. Максимальная относительная погрешность (0,05 или 5%) имеет место в конце шкалы, там, где располагаются распределения, близкие по форме к kosh (Коши). 

 

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

Преобразование рангов ИШ, полученное в результате линеаризации, имело своей целью визуализацию скрытых закономерностей структуры исследуемых шкал. Предполагалось, что выявленные закономерности могут быть объяснены либо с физической, либо с информационной точек зрения.

 

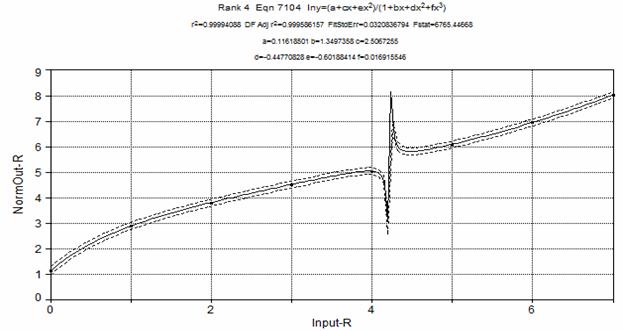
Рис. 5. Модель связи между рангами линеаризированной (NormOut-R) и исходной (Input-R) ИШ FRaSH-тестера.

 

В подтверждение вывода о том, что операция преобразования рангов чувствительна к неоднородностям ИШ, может служить график (рис. 5), представляющий собой аналитическую модель зависимости (рис. 3, В). Этот график не только визуализирует неоднородные участки, но также позволяет довольно точно оценить границу (Input-R = 4,2,) раздела двух неоднородностей. Указанная граница соответствует в табл. 2 рангу Rank = 5,2, поскольку в таблице ранги начинаются с 1, а не с 0, как на графике рис. 5. Физический смысл такого поведения зависимости (рис. 5) состоит в том, что на первом участке (R = 1..4) расположены распределения, принадлежащие к классу ограниченных (2mod, asin, even, trap, simp). На втором участке (R = 5..7) группируются распределения, принадлежащие к классу неограниченных (gaus, lapl, kosh).  

 

Таблица 3

Преобразованные значения рангов реперных точек ИШ

Исходные ранги	Имя реперной точки	Значение реперной точки	Преобразованные ранги	Приращения рангов	Нормализованные ранги	Классы	Подклассы
1	2mod	4	1853	1853	1,10825	Ограниченные распределения	Модальные
2	Asin	6,28	4823	2970	2,88457		Немодальные
3	Even	8	6305	1482	3,77093
4	Trap	10	7513	1208	4,49342
5	Simp	12	8376	863	5,00957
6	Gaus	19	10091	1715	6,03529	Неограниченные распределения	-
7	Lapl	36	11595	1504	6,93481
8	Kosh	3000	13378	1783	8,0012
8	-	10,48	9,18	11,3	9,18	Параметр формы Afrm
even	-	trap	trap	simp	trap	Форма распределения

 

Более подробную классификацию можно ввести, если проанализировать наклон отдельных участков зависимости рис.3, В. В частности, по графику (рис. 3, В) можно выделить 3 подкласса  распределений. Первому участку (Input-R, от 0 до 1) принадлежат ограниченные модальные распределения типа двумодального (2mod) и Бернулли (bern). На втором участке (Input-R, от 1 до 4) располагаются ограниченные немодальные распределения типа арксинусного (asin), равномерного (even), трапецевидного (trap) и треугольного (simp). Третьему участку (Input-R, от 4 до 7) принадлежат неограниченные распределения с «хвостами» типа нормального (gaus), двустороннего экспоненциального (lapl) и Коши (kosh). Более полная картина полученных результатов с использованием количественных и качественных показателей представлена в табл. 3.

 

ВЫВОДЫ

1. Показано, что физический смысл операции линеаризации состоит в обнаружении и визуализации значимых классификационных неоднородностей ИШ, что подтверждается сравнением графиков рис. 2,  рис. 3,В и рис. 5.

2. Подтверждается справедливость принципа масштабной инвариантности идентификационных чисел, поскольку распределение нормализованных рангов (6-я колонка, табл. 4) равно распределению преобразованных рангов (4-я колонка, табл. 4), связанных между собой масштабным коэффициентом.

Таблица 4

Распределения рангов и идентификационных параметров ИШ

Показатель	Исходная ИШ		Преобразованная ИШ
	Ранги	Значения	Ранги	Значения
Параметр формы, Afrm	8	10,48	9,18	8
Имя распределения	even	trap	trap	even

 

3. Выяснено, что ранговые распределения исходной (табл. 2) и линеаризованной (табл. 3, колонка 4) ИШ взаимно инвертируют свои значения (табл. 4). Другими словами, существует закономерность, при которой неравномерное распределение значений идентификационных чисел, в результате линеаризации, заменятся неравномерным распределением рангов.

4. Показано, что распределение рангов преобразованной шкалы (trap/9,18), более равномерно, чем распределение значений у исходной (trap/10,48) ИШ (табл. 4).

Перспективы использования предложенного способа линеаризации связаны с унификацией представления ИШ любой физической и информационной природы в виде ранговых передаточных функций (рис. 3, В). Эти функции являются безразмерными числовыми характеристиками, сохраняющими свойства исходных шкал и, поэтому, их удобно использовать для сравнения различных типов ИШ между собой.

 

ЛИТЕРАТУРА

 

1.            Пфанцагль И. Теория измерений. – М.: Мир, 1976.

2.            Пиотровский Я. Теория измерений для инженеров: Пер. с польск. - М.: Мир, 1989.

3.            Интернет-ресурс (Сайт): http://www.chemport.ru

4.            Куинн Т. Температура: Пер. с англ. – М.: Мир, 1985. – 448 с.

5.            Кликушин Ю.Н., Кошеков К.Т. Идентификационная шкала распределений как аналог таблицы химических элементов. // Омский Научный Вестник – Омск: Изд-во ОмГТУ, №1(34), 2006, с.139-147.

6.        Кликушин Ю.Н. Технологии идентификационных шкал в задаче распознавания сигналов: монография / Ю.Н. Кликушин. - Омск: Изд-во ОмГТУ, 2006. - 96 с.

7.        Кликушин Ю.Н., Кошеков К.Т. Методы и средства идентификационных измерений сигналов:  монография / Ю.Н. Кликушин, К.Т. Кошеков.  – Петропавловск: Изд-во СКГУ им. М. Козыбаева, 2007. – 186 с.

8.        Кликушин Ю.Н. Идентификационные инструменты анализа и синтеза формы сигналов: монография / Ю.Н. Кликушин. – Омск: Изд-во ОмГТУ, 2010. – 216 с.

9.        Горшенков А.А., Кликушин Ю.Н. Представление моделей сигналов в системе идентификационных параметров.// Интернет-ресурс (Электронный журнал) - Журнал Радиоэлектроники. - М.: Изд-во ИРЭ РАН, № 9 (сентябрь), 2010 г.- http://jre.cplire.ru/jre/sep10/3/text.html