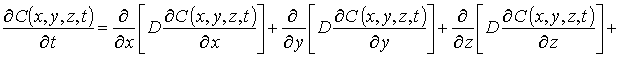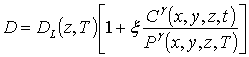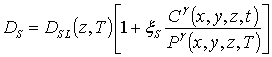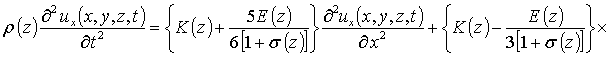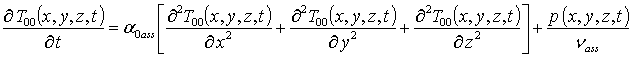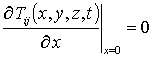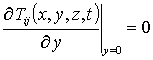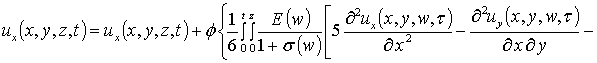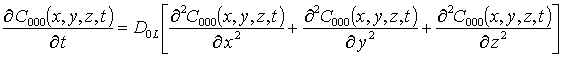Влияние механических напряжений в полупроводниковой гетероструктуре на плотность p-n-переходов

 

Е. Л. Панкратов

Нижегородский архитектурно-строительный университет

Получена 31 мая 2011 г.

 

Аннотация. Ранее было показано, что многослойность полупроводниковой гетероструктуры и оптимизация длительности отжига позволяют уменьшить глубину залегания p-n-переходов и увеличить равномерность распределения примеси в легированной области. Ранее также было показано, что механические напряжения в гетероструктуре влияют на форму распределения примеси в направлении, перпендикулярном границам раздела гетероструктуры. В данной работе рассматривается способ увеличения плотности p-n-переходов на поверхности гетероструктуры за счет использования механических напряжений.

Ключевые слова: увеличение резкости p-n-переходов; увеличение плотности p-n-переходов; оптимизация отжига; влияние напряжений между слоями гетероструктуры.

Abstract. It has been recently shown, that inhomogeneity of semiconductor heterostructure and optimization of annealing time leads to decrease depth of p-n-junctions and to increase homogeneity of dopant distribution in doped area. It has been also recently shown, that mechanical stress in two layer heterostructure (substrate and epitaxial layer) changes dopant distribution in heterostructure in directions, which are perpendicular to interface between layers of heterostructure, in comparison with unstressed sample. In this paper we consider an alternative approach to increase density of p-n-junctions in the same heterostructure by using overlayer. The overlayer leads to additional mechanical stress and as being due to increasing of density of p-n-junctions in the heterostructure.

Keywords: increasing of sharpness of p-n-junctions; increasing of density of p-n-junctions; optimization of annealing; influence of stress between layers in heterostructure.

 

Введение

Одной из актуальных задач твердотельной электроники является уменьшение размеров элементов интегральных схем (ИС), таких как p-n-переходы, транзисторы и т.д. [1-3]. При этом представляет интерес как уменьшение глубины залегания элементов ИС, так и их плотность. Для уменьшения размеров элементов ИС традиционно используются приповерхностные типы отжигов (лазерный и микроволновый) и дефектность легируемой структуры. В работах [4,5] рассмотрен альтернативный способ уменьшения глубины залегания p-n-переходов. В рамках данного метода рассматривается двухслойная гетероструктура (Г), состоящая из подложки (П) с известным типом проводимости (n или p) и эпитаксиального слоя (ЭС). В ЭС диффузионно вводится примесь, формирующая в нем второй тип проводимости (p или n). Далее проводится отжиг примеси для проникновения ее до П. Тогда в окрестности границы раздела формируется более резкий p-n-переход с более равномерным распределением примеси по сравнению с p-n-переходом в однородном образце. В [6] было показано, что механические напряжения, возникающие в Г из-за рассогласования постоянных решеток, влияют на плотность p-n-переходов в Г. В данной работе рассматривается Г, состоящая из П с известным типом проводимости (n или p) и ЭС (см. рис. 1). В ЭС диффузионно вводится примесь для формирования p-n-перехода в окрестности границы раздела между слоями Г. Перед началом отжига примеси ЭС заращивается покровным слоем (ПС) при низкой температуре, не приводящей к заметной диффузии примеси. Далее проводится отжиг примеси до тех пор, пока она не достигнет границы раздела между ЭС и П. В данной ситуации возрастает плотность p-n-переходов в ЭС по сравнению с результатом, полученным в [6]. Основной целью данной работы является поиск условий, при которых механические напряжения между слоями Г увеличили бы резкость p-n-перехода в направлении, перпендикулярном границам раздела Г.

 

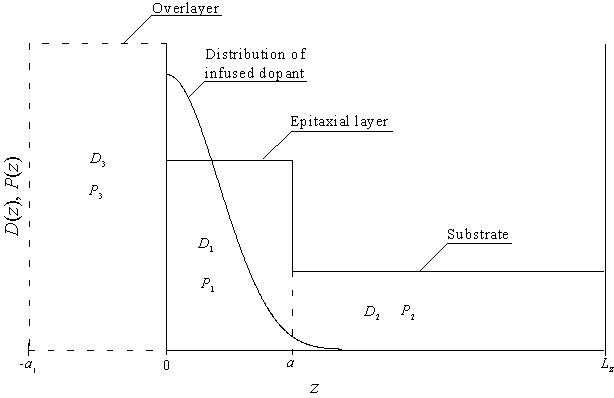
Рис. 1. Трехслойная гетероструктура, состоящая из подложки, легируемого эпитаксиального и покровного слоев. В эпитаксиальном слое приведено начальное (до отжига) распределение примеси.

 

Методика анализа

Для решения поставленной цели определим пространственно-временное распределение примеси в рассматриваемой Г и проведем его анализ. Пространственно-временное распределение примеси определялось путем решения второго закона Фика [1-3,7,8]

(1)

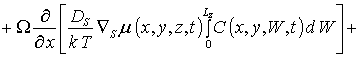
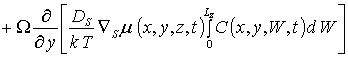
с граничными и начальным условиями

, , ,

, , ,

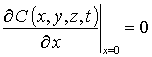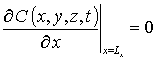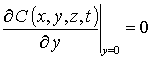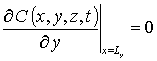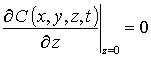C (x,y,z,0)=f_C  (x,y,z).

В данных соотношениях введены следующие обозначения: C(x,y,z,t) – пространственно-вре-менное распределение концентрации примеси; W - атомный вес примеси; символ  обозначает поверхностный градиент;  - поверхностная концентрация примеси на границе раздела между слоями; m (x,y, z,t) - химический потенциал; D и D_S – коэффициенты объемной и поверхностной (обусловленной механическими напряжениями) диффузий величина которых зависит от свойств материалов слоев Г; скорости прогрева и охлаждения Г, а также от пространственно-временного распределения концентрации примеси. Зависимость коэффициентов диффузии от концентраций примеси может быть аппроксимирована следующим соотношением [2]

, .      (2)

В данных соотношениях D_L (x,y,z,T) и D_LS (x,y,z,T) – пространственные (за счет многослойности Г) и температурные (по закону Аррениуса) зависимости коэффициентов диффузии; T – температура отжига; P (x,y,z,T) – предел растворимости примеси; определяемый свойствами материала параметр g может принимать целые значения в интервале g Î[1,3] [2]; V (x,y,z,t) - пространственно-временное распределение концентрации радиационных вакансий; V^* - равновесное распределение вакансий. Концентрационная зависимость коэффициентов диффузии подробно обсуждается в [2]. Химический потенциал может быть определен с помощью следующего соотношения [7]:

m =E(z)Ws_ij [u_ij(x,y,z,t)+u_ji(x,y,z,t)]/2,                               (3)

где E – модуль растяжения (Юнга); s_ij – тензор напряжений; 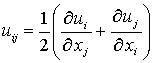 - тензор деформаций; u_i, u_j – компоненты u_x(x,y,z,t), u_y(x,y,z,t) и u_z(x,y,z,t) вектора смещений ; x_i, x_j – координаты x, y, z. Соотношение (3) может быть преобразовано к следующему виду

,

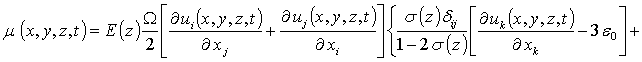
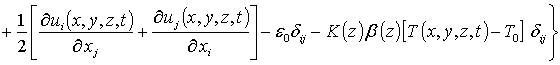где s - коэффициент Пуассона; e₀=(a_s-a_EL)/a_EL – параметр несоответствия решетки; a_s, a_EL – постоянные решёток подложки и плёнки; K – модуль всестороннего сжатия; b - коэффициент теплового расширения; T_r – совпадающая с комнатной равновесная температура. Компоненты вектора смещений могут быть определены с помощью следующей системы уравнений [8]

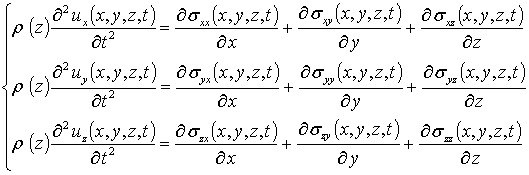
где

,

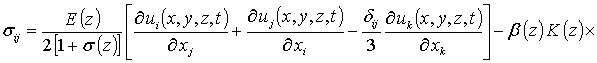
r (z) - плотность материалов МС, d_ij – символ Кронекера. С учетом такого соотношения данная система уравнений имеет вид

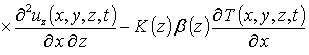
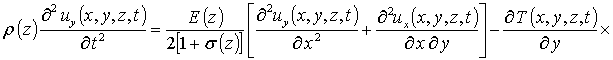
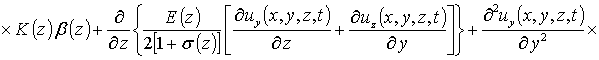
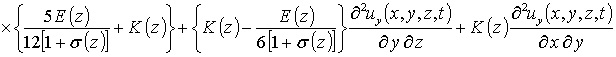              (4)

.

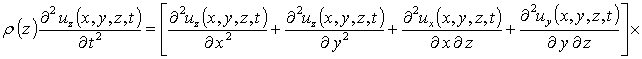
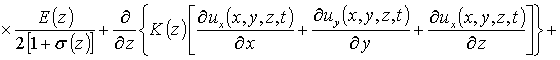
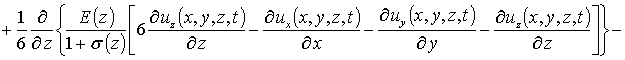
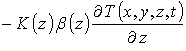Система условий для данных уравнений представима в следующей форме

; ;

; ; .

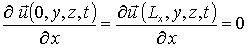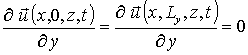Далее проведем анализ температурного поля в процессе отжига примеси. Пространственно-временное распределение температуры может быть описано с помощью соответствующего закона Фурье [9]

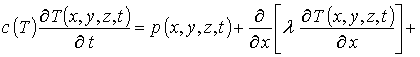
                          (5)

с граничными и начальным условиями

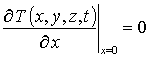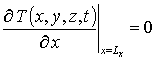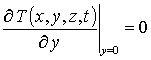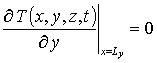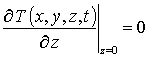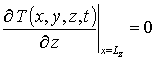, , , , , , T (x,y,z,0)=f_T  (x,y,z),

где l(z,T) - коэффициент теплопроводности, значение которого зависит как от свойств отжигаемого материала, так и от температуры. Температурная зависимость коэффициента теплопроводности в искомой области температур может быть аппроксимирована следующим образом: l(z,T)=l_ass(z)[1+m T_d^j/T^j(x,y,z,t)] (см., например, [9]). c(T)=c_ass[1-J exp(-T(x,y,z,t)/T_d)] – теплоемкость материала; T_d – температура Дебая [9]. В наиболее интересующем нас случае является сопоставимой по величине с температурой Дебая или превышает ее, что позволяет считать: c(T)»c_ass. p(x,y,z,t) – выделяющаяся в Г объемная плотность мощности. В рамках данной работы представляет интерес микроволновый отжиг. Этот тип отжига приводит к неоднородному распределению температуры [10,11], что позволяет увеличить резкость p-n-переходов и, одновременно, увеличить равномерность распределения примеси в легированной области. В данном случае целесообразно выбрать частоту электромагнитного поля таким образом, чтобы толщина скин-слоя была бы сопоставима с суммарной толщиной эпитаксиальных слоев.

На первом этапе определим пространственно-временное распределение температурного поля. Для этого следуя [4,5] представим независимый от температуры множитель коэффициента температуропроводности в виде суммы постоянной и переменной составляющих: a _ass (z) =a_0ass[1+e_T g_T(z)]. Далее будем искать решение уравнения (5) в виде следующего степенного ряда

.                                 (6)

Подстановка данного ряда в уравнение (5) позволяет получить систему уравнений для исходного приближения температуры T₀₀(x,y,z,t), а также поправочных функций к нему T_ij(x,y,z,t) (i³1, j³1) в следующей форме

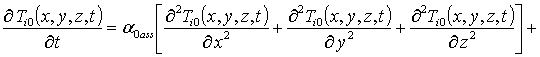
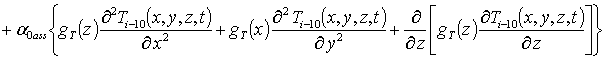, i ³1

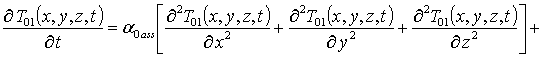
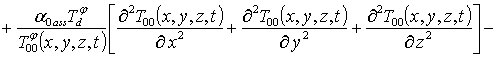           (7)

.

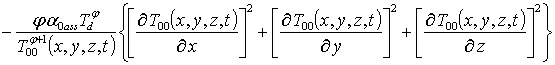
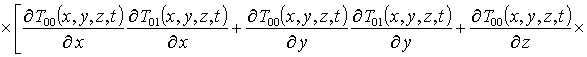
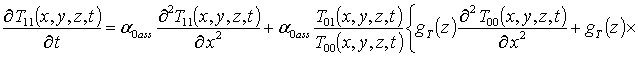
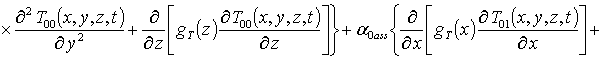
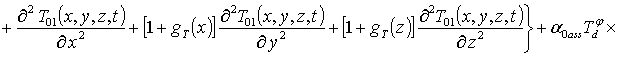
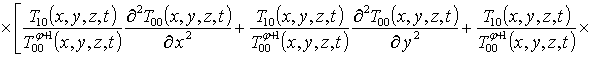
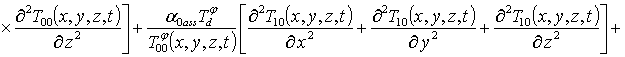
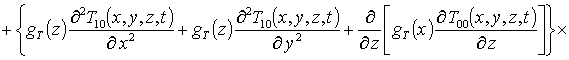
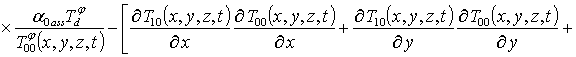
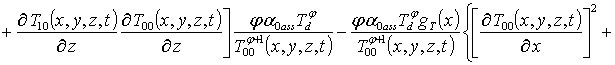
Подстановка ряда (6) в граничные и начальное условия для пространственно-временного распределения температуры преобразует их к граничным и начальным условиям для функций T_ij(x,y,z,t)

, , ,

, , ,

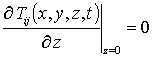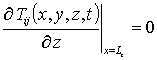T₀₀(x,y,z,0)=f_T(x,y,z), T_ij(x,y,z,0)=0, i ³1, j ³1.                                    (8)

Решение уравнений (7) с соответствующими условиями приводит к следующему результату

,

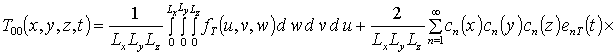
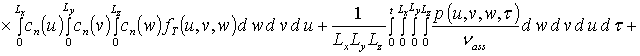
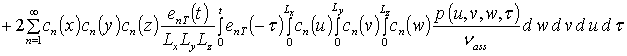где c_n(c) = cos (p nc/L), ;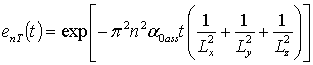

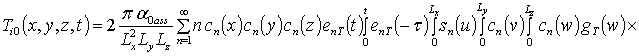
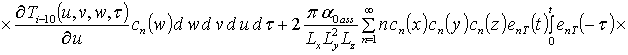
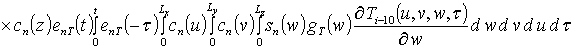, i ³1;

где s_n(c) = sin (p  n c/L);

;

 

;

 

.

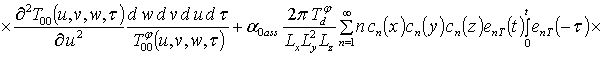
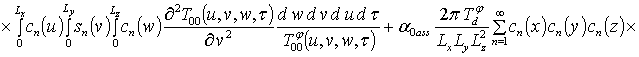
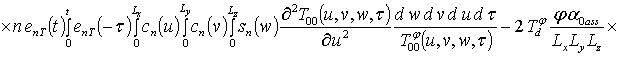
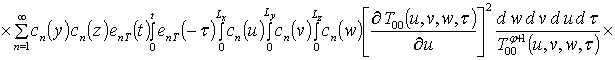
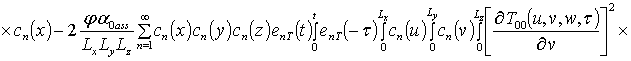
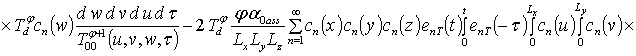
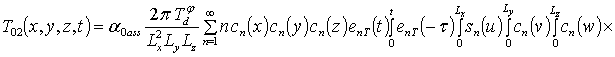
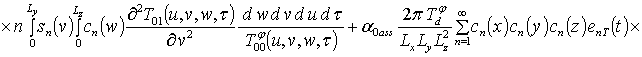
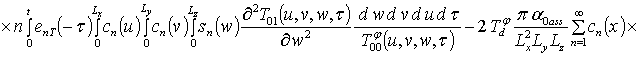
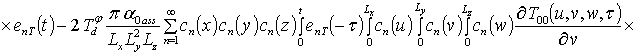
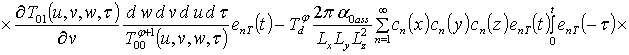
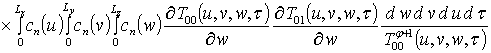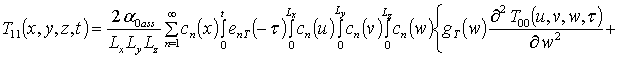
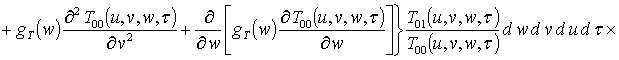
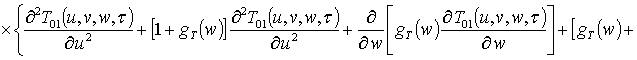
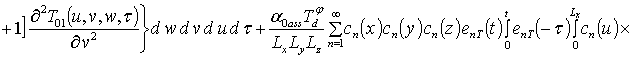
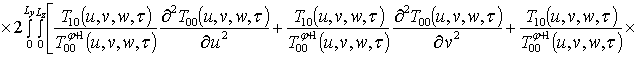
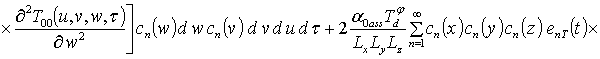
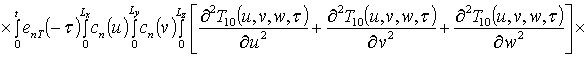
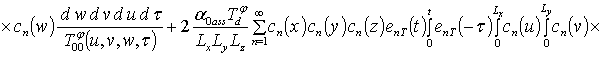
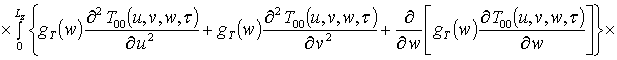
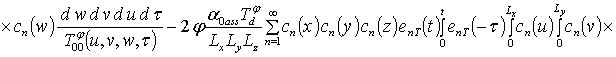
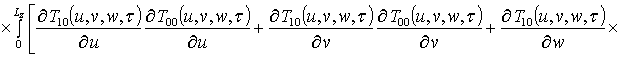
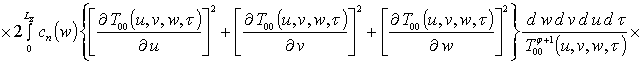
Для качественного анализа пространственно-временного распределения температурного поля, а также для некоторых количественных оценок обычно достаточно его второго приближения по параметрам, используемым в разложении (см., например, [4,5]). Аналитические результаты позволили выявить и наглядно проиллюстрировать основные зависимости. Для уточнения полученных результатов использовались численные методы.

На следующем этапе проведем оценку компонент вектора смещения. Они могут быть найдены аналогично пространственно-временному распределению температурного поля, но более компактное решение может быть получено методом осреднения функциональных поправок [13]. Предварительно уравнения системы (4) целесообразно преобразовать к следующей интегро-дифференциальной форме

,

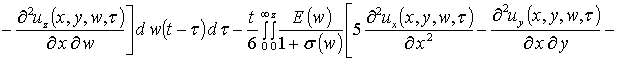
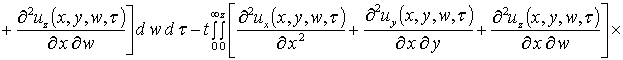
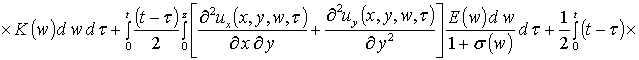
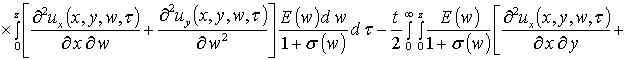
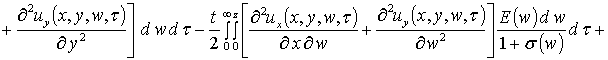
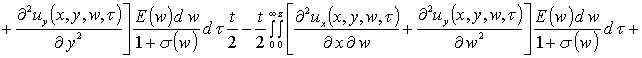
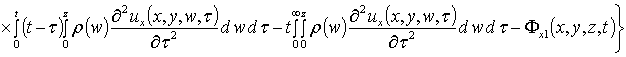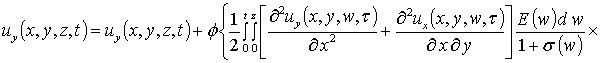
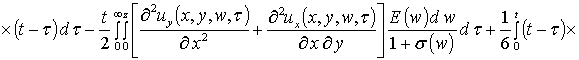
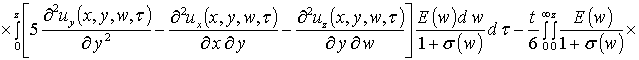
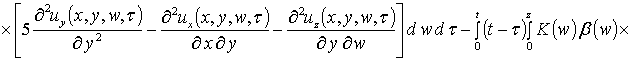
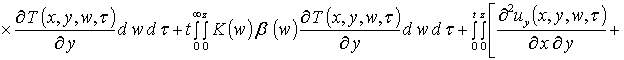
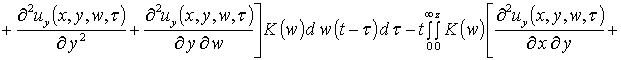
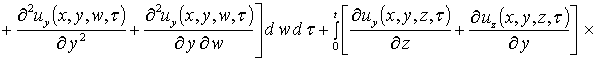
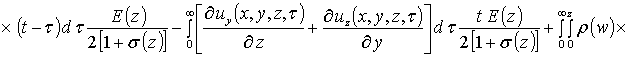
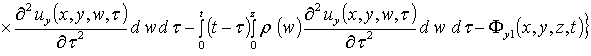, (9)

,

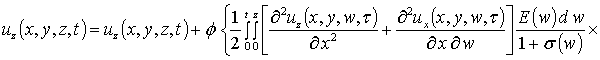
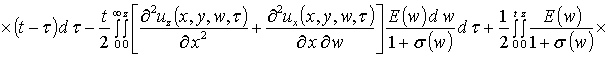
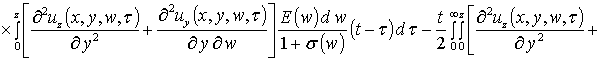
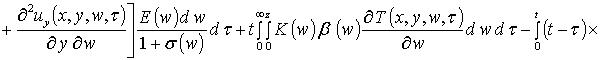
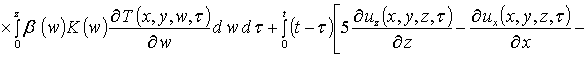
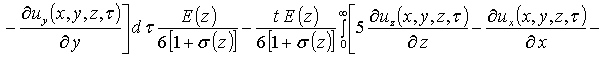
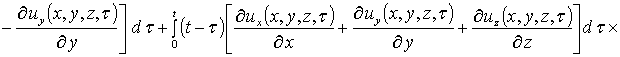
где , E₀ – среднее значение модуля Юнга, f =L/Q²E₀, s =x, y,z. Далее найдем первое приближение компонент вектора смещения. Для этого в правой части данных интегро-дифференциальных уравнений искомые функции заменим на их средние значения u_b(x,y,z,t)®a_ub1, определяемые следующим образом

a_us1=M_s1/4LQ.                                               (10)

где 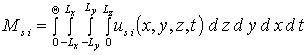. Такая замена позволяет получить

,

,

.

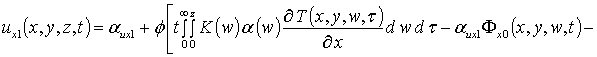
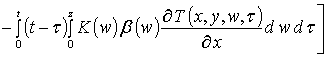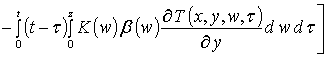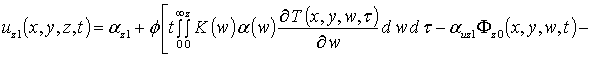
Подстановка полученных соотношений в определение средних значений (9) позволяет определить параметры a_ub1. Их значения определяются следующим образом

, ,

,

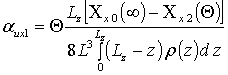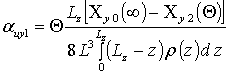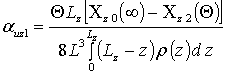где .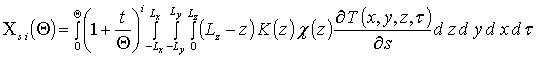

Второе приближение компонент вектора смещения может быть получено заменой в правой части уравнений (8) искомых функций u_b(x,y,z,t) на следующие суммы a_us2+u_s1(x,y,z,t), где a_us2=(M_us2-M_us1)/4L³Q. Результаты данной замены и вычисления параметров a_us2 вынесены в Приложение из-за громоздкости соответствующих соотношений.

Далее определим пространственно-временное распределение примеси путем решения уравнения (1). Для этого, следуя [4,5], представим коэффициенты диффузии D_L (z,T) и D_SL (z,T) в виде сумм D_L(z,T) =D_0L[1+e _L g_L(z,T)] и D_SL(z,T) =D_0SL[1+e_SLg_SL(z,T)], а также введем безразмерный параметр w = D_0SL/D_0L.

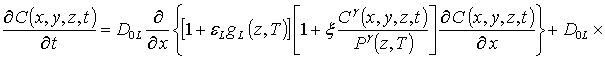
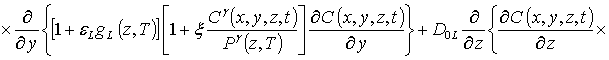
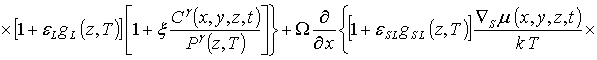
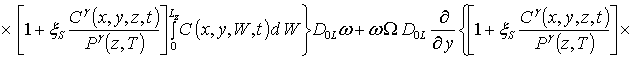
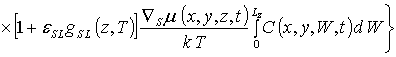.                (11)

Решение уравнения (1) определим в виде следующего степенного ряда

.                          (12)

Подстановка данного ряда в уравнение (11) позволяет получить следующую систему уравнений для исходного приближения концентрации примеси C₀₀₀(x,y,z,t), а также поправочных функций к ней C_ijk(x,y,z,t) (i³1, j³1) в следующем виде

;

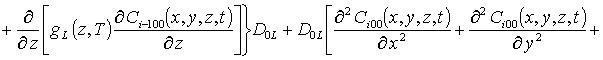
, i ³1;

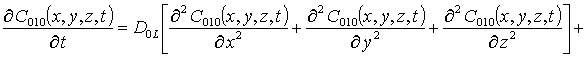
;                                 (13)

;

;

;

;

;

.

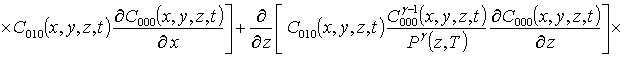
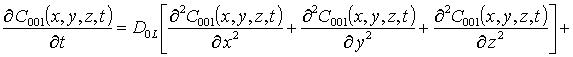
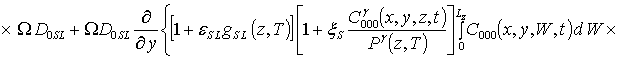
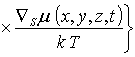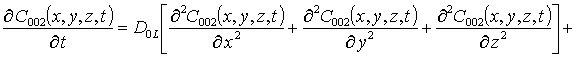
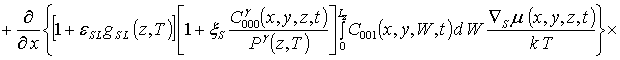
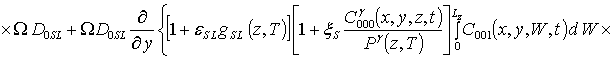
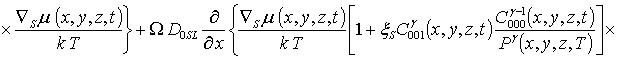
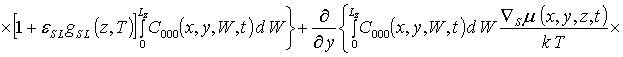
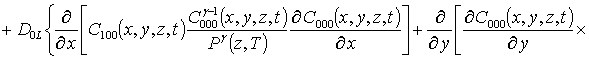
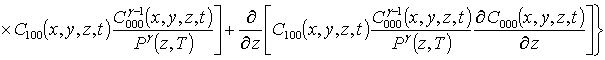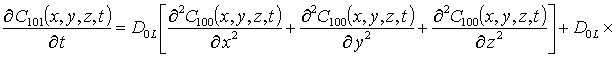
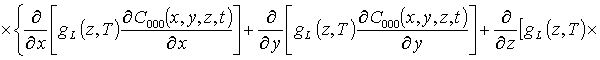
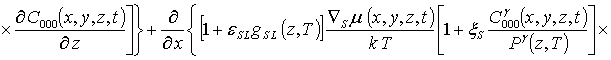
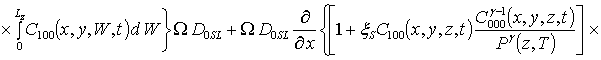
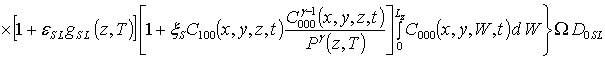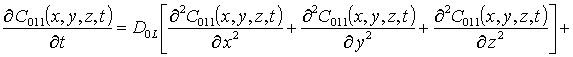
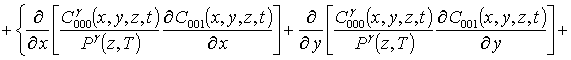
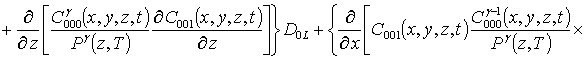
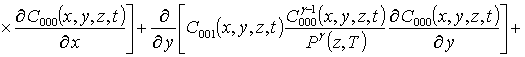
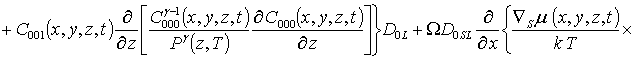
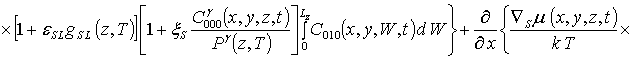
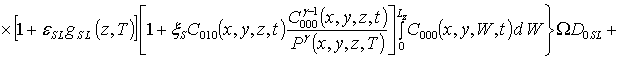
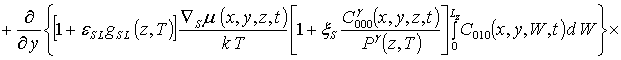
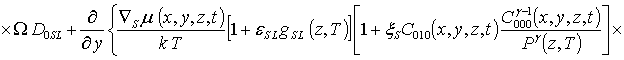
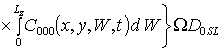Подстановка ряда (12) в соответствующие граничные и начальные условия позволяет получить для искомых функций C_ijk(x,t)

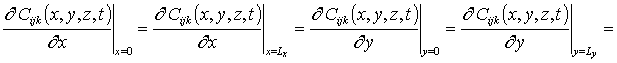
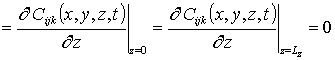; C₀₀₀(x,y,z,0)=f_C  (x,y,z); C_ijk(x,y,z,0)=0.

Решениями уравнений (13) являются следующие функции

,

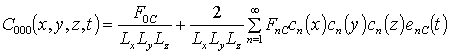где , ;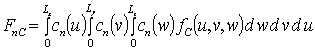

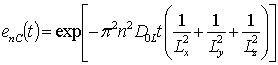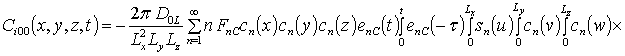
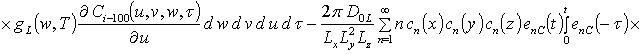
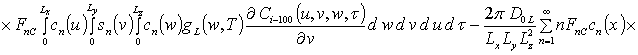
, i ³1;

;

;

;

;

;

;

.

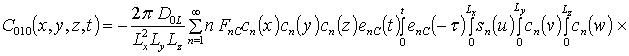
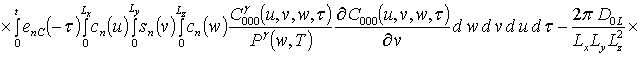
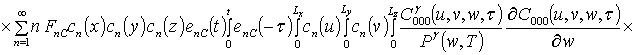
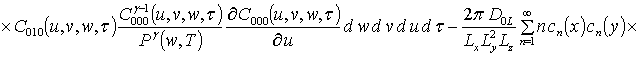
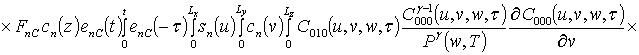
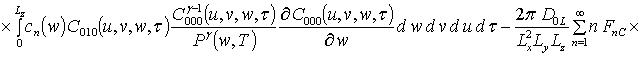
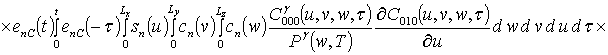
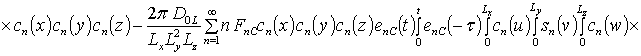
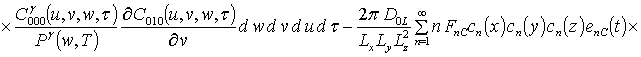
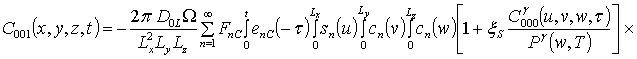
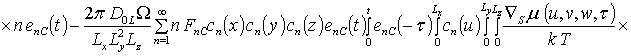
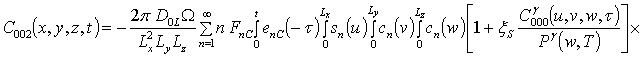
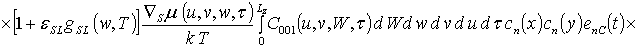
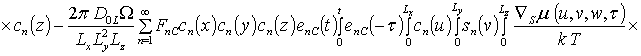
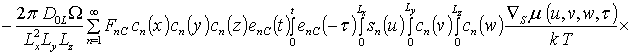
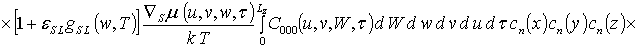
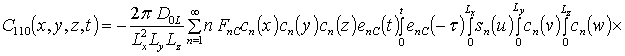
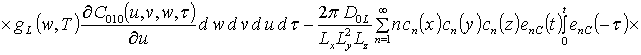
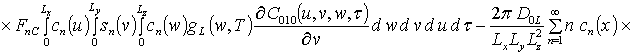
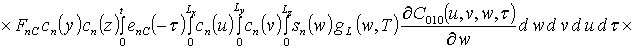
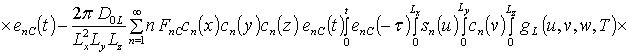
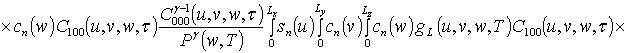
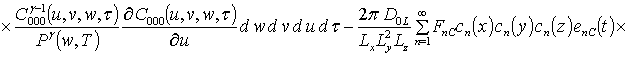
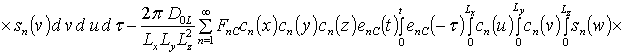
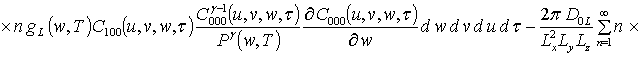
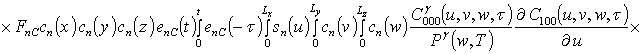
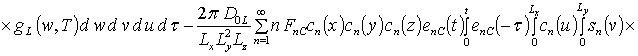
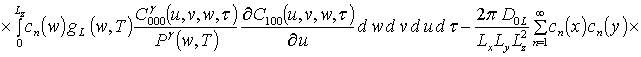
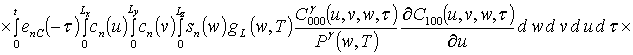
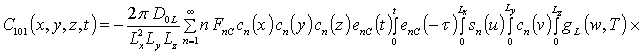
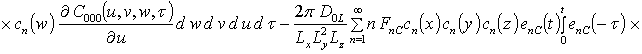
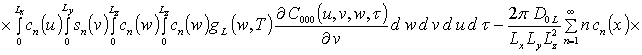
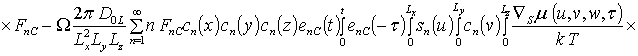
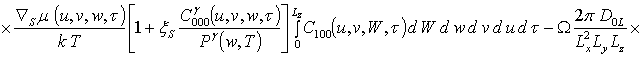
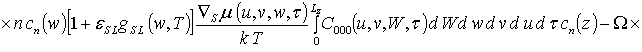
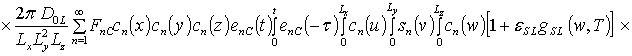
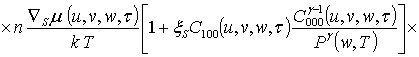
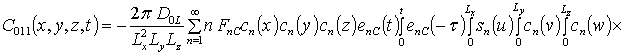
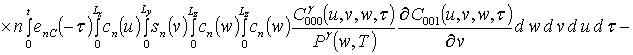
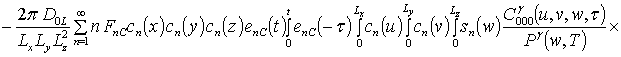
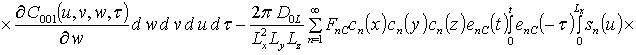
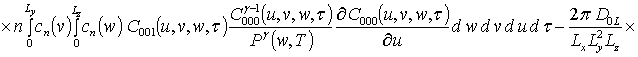
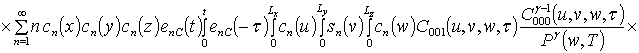
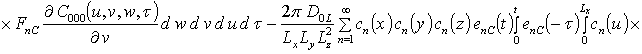
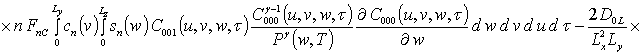
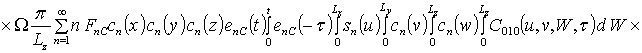
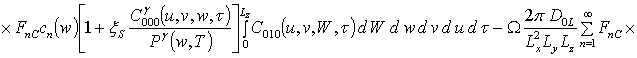
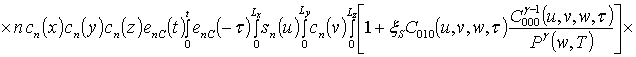
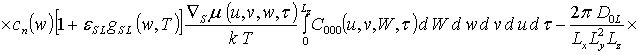
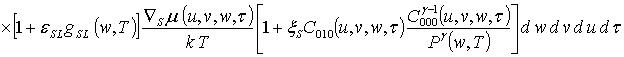Анализ пространственно-временного распределения концентрации примеси проводился аналитически во втором приближении по параметрам, используемым в соответствующем ряде, и уточнялся численно.

 

Результаты анализа

В данном разделе проведем анализ перераспределения примеси в рассматриваемой Г в течении отжига. Ранее было показано (см., например, [4-6,11]), что достижение примеси границ раздела между ЭС и П позволяет одновременно увеличить резкость p-n-перехода и равномерность распределения примеси в обогащенной ею области. На рис. 2 приведены распределения примеси в однородном материале и Г при одинаковых значениях длительности отжига. Если уменьшить длительность отжига, распределение примеси становится менее равномерным. Увеличение длительности отжига приводит к увеличению равномерности распределения примеси и снижению резкости p-n-перехода. Обе закономерности приведены на рис. 3.

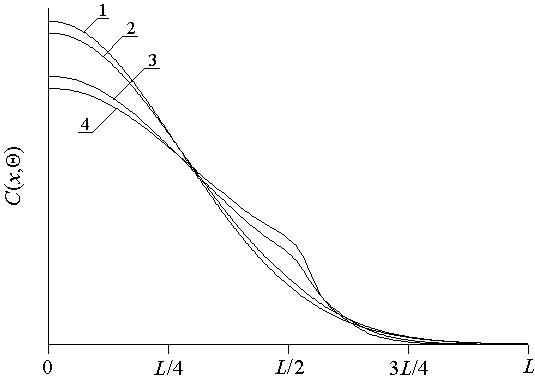
Рис. 2. Распределения примеси в однородном образце (кривая 1), а также в Г (кривые 2-4) при D₁=D₃>D₂ и среднем значением коэффициента диффузии, совпадающем с коэффициентом диффузии в однородном образце. Кривая 2 соответствует отношению D₁/D₂=1,2. Кривая 3 соответствует отношению D₁/D₂= 4,75. Кривая 4 соответствует отношению D₁/D₂=11,5.

 

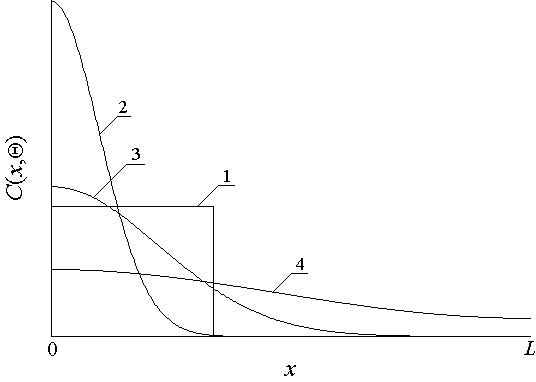
Рис. 3. Кривая 1 – идеализированное распределение примеси; кривые 2-4 – реальные распределения примеси в различные моменты времени, величина которых растет с номером кривых.

 

 

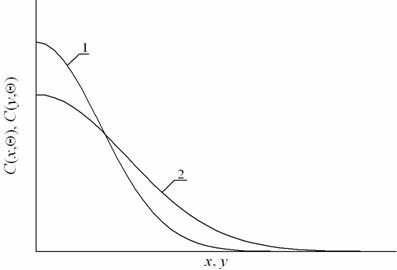
Рис. 4. Распределения примеси в направлении, перпендикулярном границе раздела между слоями Г. Кривая 1 соответствует отрицательному значению параметра несоответствия решетки между ЭС и П, а также положительному значения параметра несоответствия решетки между ЭС и ПС. Кривая 2 соответствует значениям параметра несоответствия решетки, противоположным значениям данного параметра для кривой 1.

 

 

В результате проведенного анализа было получено, что механическое напряжение в Г, возникающее за счет рассогласования постоянных решетки слоев, не приводит к качественным изменениям распределений примеси вглубь Г. Однако, механическое напряжение может привести к увеличению плотности p-n-переходов, входящих в состав ИС. Данное увеличение достигается за счет замедления боковой диффузии примеси, происходит при отрицательном значении параметра несоответствия решетки e₀ между ЭС и П, а также при положительном значении параметра несоответствия решетки e₀ между ЭС и ПС. Данная зависимость проиллюстрирована с помощью рис. 4.

Заключение

В данной работе анализ влияния механического напряжения в гетероструктуре на глубину залегания p-n-переходов и их плотность в интегральных схемах. Сформулированы условия, при которых увеличивается плотность p-n-переходов.

 

Данная работа поддержана грантом президента России (проект № МК-548.2010.2).

 

Литература

 

[1] A.B. Grebene. Bipolar and MOS analogous integrated circuit design. New York, John Wyley and Sons,1983,894p.

[2] З.Ю. Готра. Технология микроэлектронных устройств. - М.: Радио и связь. 1991. 528с.

[3] В.И. Лачин, Н.С. Савелов. Электроника. Ростов-на-Дону: Феникс, 2001. 446 с.

[4] E.L. Pankratov. Phys. Rev. B. 2005. V.72 (7). P. 075201-075208.

[5] E.L. Pankratov, B. Spagnolo. The Eur. Phys. J. B. 2005. V. 46 (1). P. 15-19.

[6] E.L. Pankratov. Mord. Phys. Lett. B. 2010. V. 24 (9). P. 867-895.

[7] Y.W. Zhang, A.F. Bower. // Journal of the Mechanics and Physics of Solids. 1999. V.47. P. 2273-2297.

[8] Л.Д. Ландау, Е.М. Лифшиц. Теоретическая физика. Т.7 (Теория упругости). М.: ФИЗМАТЛИТ, 2001.

[9] К.В. Шалимова. Физика полупроводников. М.: Энергоатомиздат, 1985. 391 с.

[10] В.Е. Кузьмичёв. Законы и формулы физики. Киев: Наукова Думка, 1989, 862 с.

[11] E.L. Pankratov. J. Appl. Phys. 2008. Vol. 103 (6). P. 064320-064330.

[12] Ю.Д. Соколов // Прикладная Механика. 1955. Т.1, С. 23-35.

Приложение

Вторые приближения компонент вектора смещения имеют следующий вид

,

,

.

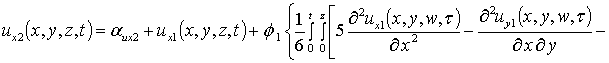
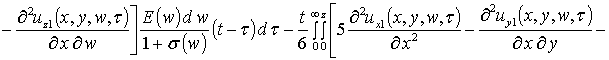
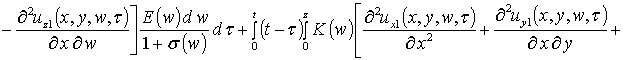
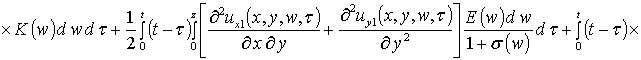
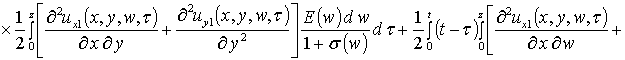
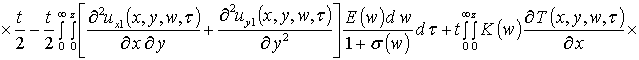
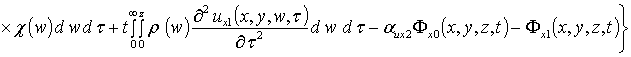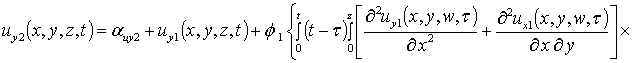
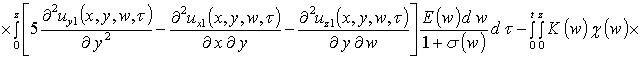
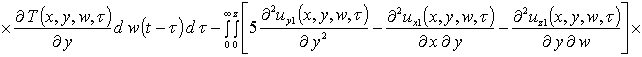
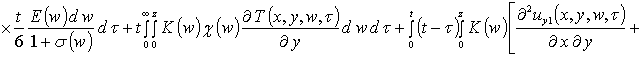
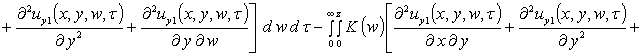
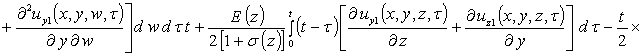
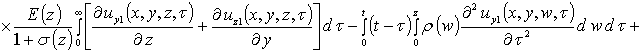
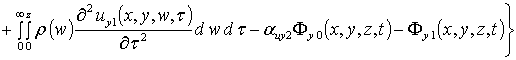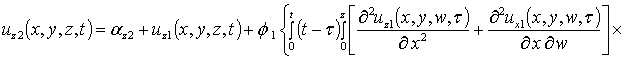
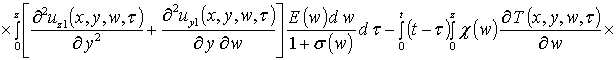
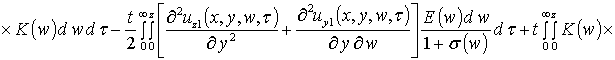
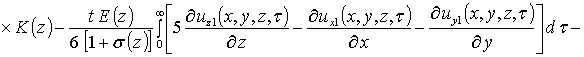
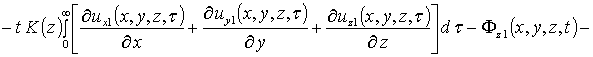
Вычисление параметров a_ub2 приводит к следующему результату

,

,

.
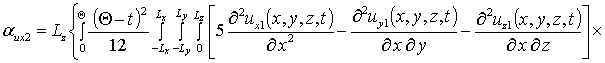
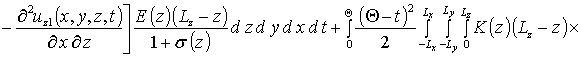
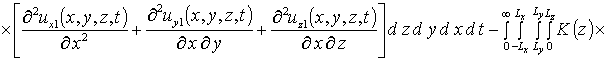
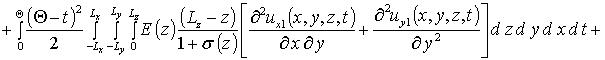
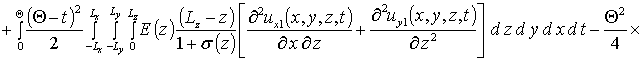
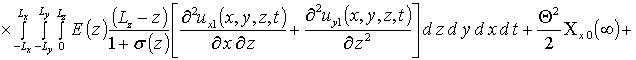
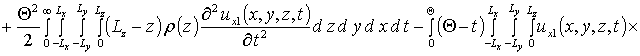
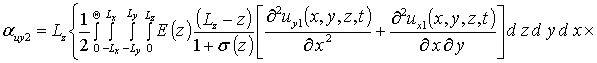
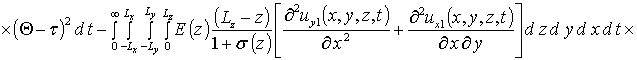
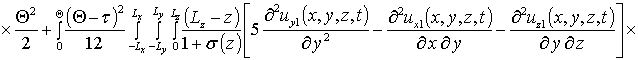
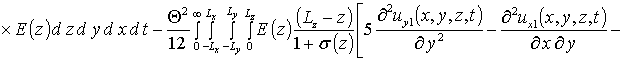
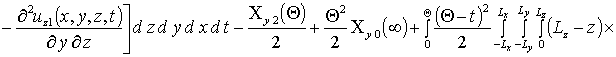
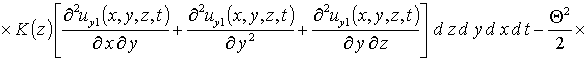
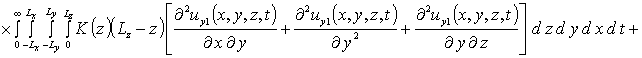
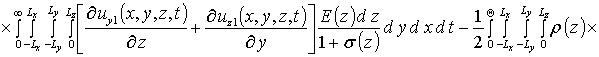
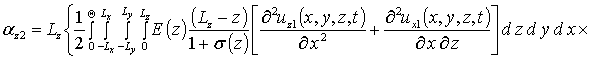
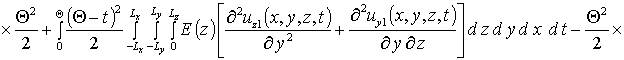
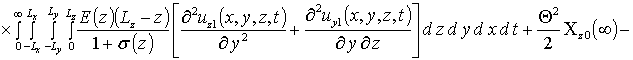
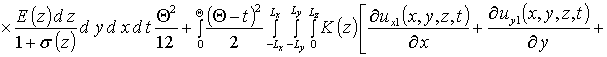
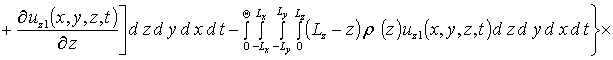