УДК 621.396.96

ОЦЕНКА ЭФФЕКТИВНОСТИ АЛГОРИТМОВ СВЕРХРАЗРЕШЕНИЯ ГРУППОВЫХ ОБЪЕКТОВ ПО ДАЛЬНОСТИ
МЕТОДОМ ПОЛУНАТУРНОГО МОДЕЛИРОВАНИЯ

 О. В. Васильченко, С. А. Климов, В. М. Косяков

 Военная академия войсковой противовоздушной обороны Вооруженных Сил Российской Федерации

имени Маршала Советского Союза А.М. Василевского, Смоленск

 

Получена 15 мая, после доработки 21 июня 2012 г.

 

Аннотация. Исследована эффективность алгоритмов сверхразрешения групповых объектов по дальности методом полунатурного моделирования с помощью имитатора сигналов группового объекта. Обобщены результаты оценки эффективности исследуемых методов сверхразрешения.

Ключевые слова: сверхразрешение, групповой объект, имитатор сигналов, эффективность.

Abstract. Efficiency of algorithms of superpermission of group objects on range by a method of semi-natural modeling by means of the simulator of signals of group object is investigated. Results of an assessment of efficiency of studied methods of superpermission are generalized.

Keywords: superpermission, group object, simulator of signals, efficiency.

 

Введение

Среди методов экспериментальных исследований известны натурные, полунатурные и методы физического (лабораторного) моделирования. Без сомнения, натурные испытания различных алгоритмов обработки радиолокационной информации могут дать наиболее глубокую и объективную оценку эффективности их функционирования. Однако, проведение подобных экспериментов, представляет собой сложную и дорогостоящую задачу, связанную со значительными затратами времени. Кроме того, требования к выполнению натурного эксперимента могут оказаться невыполнимыми на практике в силу необходимости варьирования в широких пределах условий проведения исследований. Ограничение всего многообразия реальных ситуаций в натурном эксперименте только некоторыми частными случаями делает его не эффективным.

Таким образом, представляется целесообразным в качестве метода экспериментального исследования оценки эффективности алгоритмов сверхразрешения групповых объектов по дальности использовать метод полунатурного моделирования. С одной стороны, его можно рассматривать как логическое продолжение метода математического моделирования с задачей приближения к условиям, подобным реальным. С другой стороны, метод полу натурного моделирования можно рассматривать как предварительный этап подготовки к натурному эксперименту [1].

 

Методика эксперимента

Для проведения испытаний методом полунатурного моделирования формировался узкополосный локационный сигнал, подобный отраженному эхосигналу от группового объекта. Параметры сигнала соответствовали применяемым в настоящее время параметрам зондирующих сигналов локаторов: частоты повторения десятки-тысячи килогерц, длительности импульсов единицы-десятки микросекунд, скважность единицы-сотни, длительности пачки сигналов порядка нескольких десятков миллисекунд, диапазон промежуточных частот при оцифровке радиосигнала для осуществления первичной обработки единицы-десятки мегагерц.

Под разрешением сигналов по дальности понимается указание числа сигналов, содержащихся в смеси сигнала и шума, и оценивание дальностей (времен запаздывания) каждого из сигналов.

В качестве показателя эффективности разрешения сигналов использовалась матрица условных вероятностей Р. Элементом P_ij матрицы Р является вероятность принятия решения о событии i (наличии i сигналов в составе сигнальной смеси) при условии, что в действительности имеет место событие j (результирующий сигнал представляет собой сумму j сигналов). Элементы матрицы Р (при i = j) служат условными вероятностями принятия правильных решений, а при i ≠ j – ложных решений. Ошибочные решения характеризуются вероятностью F_i превышения оцениваемого числа сигналов над истинным иx количеством (при j > i). Значение F_i определяется соотношением 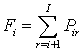(I – количество сигналов в смеси), т. е. суммой элементов i-й строки матрицы Р, следующих за элементом Р_ii.

В качестве точечной оценки для неизвестной вероятности принимается частота наступившего события. Оценка элементов матрицы Р (при i = j) определяется как относительная частота события , где  – число появления события i;  – число испытаний.

Количество независимых реализаций для исследования статистических характеристик оценок вероятности бралось не менее 100. При этом обеспечивалась точность статистического эксперимента порядка 10–12 % [2].

В качестве оценки для математического ожидания (МОЖ)  при получении оценок дальности использовалась зависимость

 

 

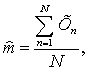
где  – значение оцениваемой величины (дальности или времени запаздывания) в n-ом испытании, а в качестве оценки для дисперсий оценок –

 

 

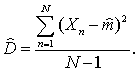
Оценки значений элементов матрицы Р, а также математических ожиданий и дисперсий измерений дальности и скорости проводились для различных отношений сигнал-шум q (ОСШ), относительной интенсивности амплитуд сигналов и относительных рассогласований сигналов по частоте  ( – рассогласование сигналов по частоте Доплера, ΔF = 50–500 Гц – ширина доплеровского фильтра) и дальности  ( – расстояние между одиночными объектами из состава группового по дальности,  – величина строба дальности, которая бралась на 20–30 % больше длительности зондирующего сигнала). Диапазон ОСШ Δq составлял 0–30 дБ (по сигналу с наименьшей амплитудой), диапазон относительной интенсивности амплитуд сигналов составлял 0–20 дБ, диапазоны относительных рассогласований сигналов по частоте и дальности – 0,1–1.

 

Проведение эксперимента

Имитатор сигналов группового объекта реализован в виде электронного устройства (стенда), включающего набор генераторов, импульсных модуляторов, генератор шума и сумматор (рис. 1).

С помощью генераторов и сумматора на операционном усилителе формировались модели эхосигналов одно- и двухточечного рассеивателей на выходе усилителя промежуточной частоты радиолокатора – когерентные пачки простых радиоимпульсов с прямоугольной огибающей.

Сформированная на промежуточной частоте модель эхосигнала оцифровывалась с помощью субмодуля цифрового приема ADMDDC2WB-L и поступала на обработку в ПЭВМ. В состав субмодуля ADMDDC2WB-L входил аналого-цифровой преобразователь и преобразователь дискретных отсчетов сигнала в отсчеты квадратурных составляющих комплексной огибающей эхосигнала DDC AD6620.

Отношение сигнал-шум регулировалось программно: подмешиванием к оцифрованному эхосигналу цифрового шума требуемой мощности. Такой подход позволяет минимизировать количество файлов для хранения результатов эксперимента.

 

 

Рис. 1. Экспериментальная установка для исследования
эффективности разрешения сигналов методом полунатурного моделирования

 

Оценка разрешающей способности по дальности предполагала вычисление трех показателей: оценки значений элементов матрицы Р (определялись значения вероятности правильного разрешения (P₂₂) при фиксированном значении ложной тревоги (P₁₂ = 0,05)), математических ожиданий и дисперсий измерений дальности при относительных рассогласованиях сигналов по частоте  близких к нулевому значению и различных по дальности  (рис. 2) при изменяющемся ОСШ в интервале от 10 до 30 дБ. Анализировались также возможности разрешения объектов стандартными методами обработки сигналов.

Стандартный или визуальный способ определения количества сигналов в обрабатываемой выборке основан на анализе перегибов (локальных максимумов) огибающей автокорреляционной функции (АКФ). Предполагается, что на этапе обнаружения принято решение о наличии полезного сигнала в обрабатываемой реализации, затем проводится этап анализа огибающей АКФ и принимается решение о количестве сигналов, присутствующих в данной реализации.

 

 а                                                                    б

Рис. 2. Осциллограммы напряжений сигналов для исследования эффективности разрешающей способности по дальности при отсутствии шума: а – два сигнала при относительном рассогласовании их по времени равном 0,5; б – два сигнала при относительном рассогласовании их по времени равном 0,1

 

Исходя из этого на первом этапе исследовалась процедура обнаружения смеси сигналов с показателями качества не ниже заданных. Наличие сигналов определялось нахождением локальных максимумом огибающей АКФ при вероятности ложной тревоги P₁₂, не превышающей 0,05, и соответствующим порогом обнаружения. Результаты представлены на рис. 3.

Следующим способом, подлежащим сравнительной оценке, был выбран компенсационный способ, описанный в [3]. Основной особенностью способа являлось то, что обработка принятого сигнала проводилась в области основного лепестка после стандартной процедуры фильтрации. Порог обнаружения устанавливался исходя из значения вероятности ложного обнаружения сигнала одиночного объекта, равного 0,05. При превышении порога хотя бы в одном стробе дальности принималось решение об обнаружении сигнала группового объекта. Результаты представлены на рис. 4.

Следующий способ анализа описан в [4]. Сущность способа заключается в том, что после проведения процедуры стандартной корреляционной обработки сформированный при этом сигнал умножают на заранее рассчитанную автокорреляционную матрицу и сравнивают модуль полученного произведения с порогом. При превышении порога принимается решение об обнаружении группового объекта. Способ основан на проекционном методе решения обратной задачи [4]. Результаты оценки его эффективности представлены на рис. 5.

Обобщенные результаты, демонстрирующие характер изменения вероятностей P₂₂ для разных относительных отстояний сигналов δD после обработки исследуемыми алгоритмами в зависимости от ОСШ q, представлены графически на рис. 6.

 

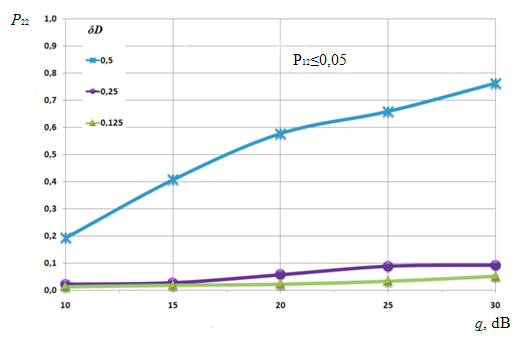
Рис. 3. Кривые разрешения, полученные с помощью стандартного алгоритма

 

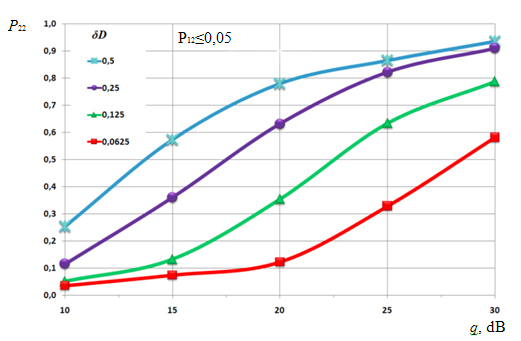
Рис. 4. Кривые разрешения, полученные с помощью компенсационного способа

 

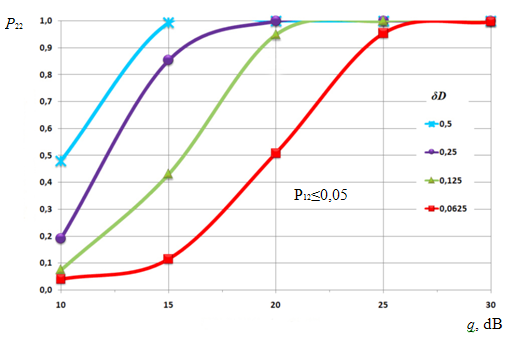
Рис. 5. Кривые разрешения, полученные с помощью проекционного способа

 

Анализируя графические зависимости, представленные на рис. 3–6, можно сделать следующие предварительные заключения:

обработка стандартным алгоритмом не позволяет разрешать сигналы по времени с заданными показателями качества при относительных отстояниях, меньших 0,5;

обработка компенсационным способом позволяет получить достаточно высокие показатели разрешающей способности при высоких ОСШ;

обработка проекционным методом, позволяет получить высокие показатели разрешающей способности на интервале ОСШ.

После обобщения результатов оценки эффективности были получены эмпирические зависимости относительного интервала разрешения от ОСШ для исследуемых методов. Для сравнения алгоритмов разрешения сигналов использовался потенциальный относительный интервал разрешения (ПОИР) [4, 5]. Результаты представлены также на рис. 6.

 

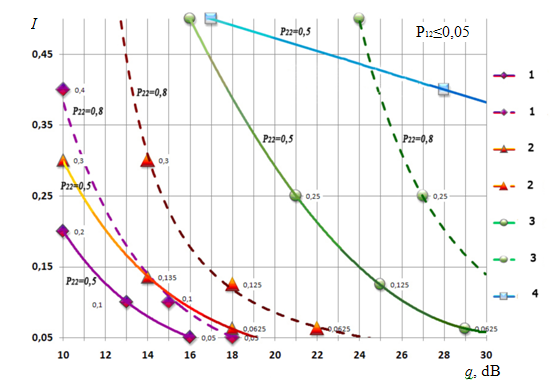
Рис. 6. Оценки разрешающей способности алгоритмов обработки сигналов со сверхрелеевским разрешением области для двух целей: I – относительный интервал разрешения,   1 – ПОИР, 2 – проекционный метод, 3 – компенсационный метод, 4 – стандартная обработка.

 

Было также исследовано поведение оценок дальностей в зависимости от относительных рассогласований сигналов по дальности. На рис. 7 и 8 показаны МОЖ  и среднеквадратичные ошибки (СКО)  оценок соответственно, нормированные к величине строба дальности. При исследовании ОСШ составляло 18 дБ.

 

Рис. 7. МОЖ оценок дальностей в зависимости от относительного

рассогласования сигналов по дальности

 

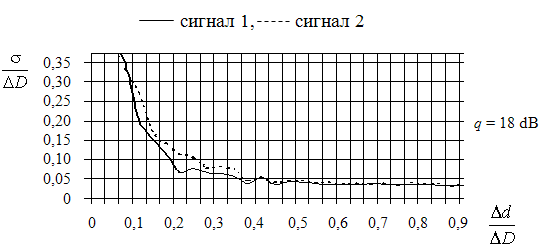
Рис. 8. СКО оценок дальностей в зависимости от относительного

рассогласования сигналов по дальности

 

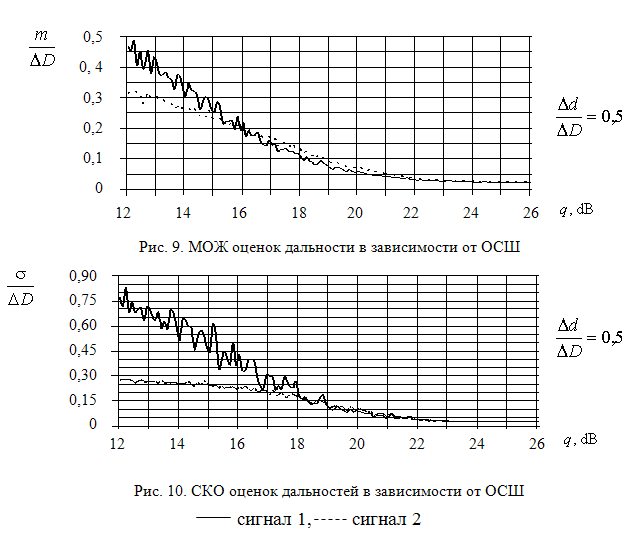
На рис. 9 и 10 показаны зависимости МОЖ и СКО оценок измерения дальности соответственно в зависимости от ОСШ. Последнее рассчитывалось по сигналу с наименьшей амплитудой и на графиках представлено в логарифмическом масштабе. При этом относительное рассогласование сигналов по дальности составляло .

Анализ полученных на рис. 7–10 зависимостей позволяет заключить, что дисперсия и смещенность оценок дальности отдельных объектов из состава групповой после определения ее количественного состава снижаются как с повышением ОСШ, так и при увеличении относительного рассогласования сигналов по дальности.

Если допустить, что полученные выше оценки не превышали заданной величины, например, МОЖ  и СКО  для каждого объекта одновременно, то заданные показатели качества оценивания достигаются при ОСШ q равном 18 дБ и относительном рассогласования сигналов по дальности  (см. рис. 7, 8). С другой стороны, анализ зависимостей на рис. 9, 10 позволяет утверждать, что заданные выше показатели качества оценивания достигаются при относительном рассогласования сигналов по дальности , если ОСШ составляет примерно 16 дБ.

Выводы

Методом полунатурного моделирования с помощью имитатора сигналов групповой цели доказана эффективность алгоритмов сверхразрешения сигналов по дальности. Полученные результаты оценки исследуемых методов сверхразрешения значительно превосходят классические методы.

Проведенные исследования показали, что для локаторов со сверхразрешением по дальности при реализации цифровой обработки сигналов наиболее эффективно применение проекционного метода.

 

Литература

1. О моделировании вторичного излучения воздушных целей и его использовании в технике радиолокационного распознавания: Научно- технические серии/ Ширман Я. Д., Лещенко С. П., Орленко В. М. 2000. № 2. Вып. 3. С. 65-74.

2. Колмогоров А. Н. Основные понятия теории вероятностей. – М.: Наука. 1974. – 120 с.

3. Абраменков В. В. Измерение координат радиолокационных целей методами многосигнальной радиолокации: моногр. Смоленск, ВУ ВПВО ВС РФ, 2002.

4. Чижов А. А. Сверхрэлеевское разрешение. Т. 2. Преодоление фактора некорректности обратной задачи рассеяния и проекционная радиолокация. М., Красанд, 2010. 104 с.

5. Чижов А.А. Сверхрэлеевское разрешение. Т. 1: Классический взгляд на проблему. М. КРАСАНД, 2010. 96 с.