УДК 537.874

СИСТЕМА ИЗ ДВУХ УГЛЕРОДНЫХ НАНОТРУБОК КАК АНТЕННА И ДЕТЕКТОР ТЕРАГЕРЦЕВОГО ИЗЛУЧЕНИЯ

 

В. Л. Семененко¹, В. Г. Лейман¹, А. В. Арсенин¹, Ю. В. Стебунов¹, В. И. Рыжий²

¹ Московский физико-технический институт (государственный университет), Лаборатория нанооптики и фемтосекундной электроники

² Университет Тохоку, Сендай, Япония

Получена 4 июня 2012 г.
 

Аннотация. Рассмотрена система из двух одинаковых, параллельно расположенных и консольно закрепленных однослойных углеродных нанотрубок с металлической проводимостью в поле волны терагерцевого излучения. Найдены вынужденные колебания электронной плазмы в нанотрубках для случаев монохроматического и модулированного излучения. Вычислены параметры нанотрубок как механических резонаторов. Показано, что рассматриваемая система нанотрубок может служить достаточно чувствительным резонансным детектором модулированного терагерцевого излучения. Оценена пороговая амплитуда немодулированного терагерцевого излучения, принимаемого детектором, при которой возникает самовозбуждение механических колебаний нанотрубок.

Ключевые слова: терагерцевое излучение, детектор, углеродная нанотрубка, контактное сопротивление.

Abstract. The system of the two same, placed side-by-side and double clamped single-walled carbon nanotubes with metallic conductivity in the electromagnetic field of modulated and non-modulated terahertz radiation is considered. Forced oscillations of the carbon nanotubes electron plasma are calculated. The lumped parameters of the mechanical resonators that the nanotubes represent by themselves are determined. It is shown that the considered system of the nanotubes can serve as a detector of modulated terahertz radiation. The responsivity of the detector is estimated. The threshold value of the electric field amplitude of the incoming monochromatic terahertz radiation, above which the self-excitation of the nanotube mechanical resonators occurs is estimated.

Keywords: terahertz radiation, sensor, carbon nanotube, contact resistance.

 

Введение

Терагерцевое излучение имеет существенный потенциал для использования в различных приложениях [1]. Недавно был предложен ряд устройств для детектирования модулированного терагерцевого излучения, основанных на концепции полевого транзистора с механически подвижным упругим затворным электродом [2-5]. Такие устройства имеют малый размер (~ 1 мкм) и может перестраиваться в пределах всего терагерцевого диапазона. Высокая чувствительность таких устройств может быть достигнута при использовании в качестве механических кантилеверов однослойных углеродных нанотрубок (ОУНТ) [4, 5]. Однако, возбуждение колебаний электронной плазмы в нанотрубках подавляется из-за наличия высокого контактного сопротивления ( кОм). Для достижения более высокого значения добротности плазменных колебаний мы предлагаем новую схему устройства, в котором возбуждение плазменных колебаний реализуется без электрических контактов. В этой схеме электрическое поле терагерцевого излучения, падающего на устройство непосредственно воздействует на электронную плазму в нанотрубках и возбуждает ее колебания (рис. 1).
 

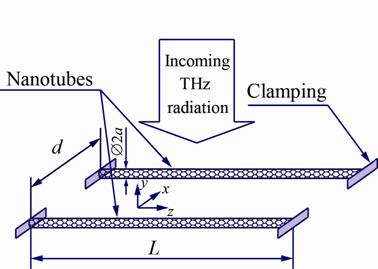
Рис. 1. Система из двух ОУНТ в электромагнитном поле
терагерцевого излучения.
 

Перераспределение электрического заряда в нанотрубках приводит к возникновению силе отталкивания между ними, которая квадратична по величине входящего сигнала, который несет терагерцевая волна. Ввиду этой нелинейности, спектр механической силы взаимодействия между нанотрубками содержит низкочастотные гармоники модулирующего сигнала. Таким образом, если спектр сигнала модуляции попадает в резонансную полосу механического резонанса, последний возбуждается и тем самым происходит конвертация модулирующего сигнала в механические колебания нанотрубок, т.е. демодуляция входящего сигнала. Также, как известно, в подобных системах может возникать самовозбуждение низкочастотного (механического) резонатора даже в отсутствие модуляции высокочастотной несущей гармоники входящего сигнала [6, 7]. В этой работе мы предлагаем модель, описывающую рассматриваемое устройство как систему из двух связанных резонаторов, плазменного и механического. В случае модулированного ТГц излучения, падающего на систему, мы рассчитываем амплитуду их механических колебаний и предлагаем схему для их измерения (детектирования). Также, мы оцениваем пороговую величину амплитуды электрического поля входящей монохроматической терагерцевой волны, при превышении которой происходит самовозбуждение механических колебаний нанотрубок.

 

Вынужденные колебания электронной плазмы в нанотрубках

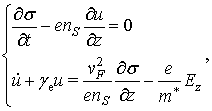                                                 (1)                                                             

где  ‑ поверхностная концентрация свободных электронов в нанотрубках,  ‑ частота столкновения электронов,  ‑ скорость Ферми,  ‑ эффективная масса электрона,  ‑ проекция макроскопического электрического поля на ось , направленную вдоль нанотрубок,  ‑ модуль заряда электрона.

Решая совместно (1) с уравнениями Максвелла и граничными условиями на поверхности нанотрубок

                                                      (2)                                                            

где  ‑ компонента вектора электрического поля, направленная вдоль нормального вектора  к поверхности нанотрубок, можно получить дисперсионное соотношение для плазменных волн, бегущих вдоль рассматриваемой системы из двух нанотрубок:

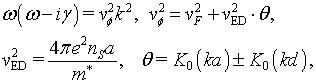                            (3)                                           

где  ‑ радиус нанотрубок,  ‑ расстояние между их осями,  and  ‑ волновой вектор и частота соответственно. Знак “+” в выражении для  соответствует симметричной волне, знак “‑” ‑ антисимметричной. Последняя широко распространена в радиотехнических приложениях, так как она распространяется в самого различного рода двухпроводных линиях. Соотношение (3) получено в предположении аксиально симметричного распределения плотности заряда в нанотрубке, что справедливо, при . Кроме того, предполагается, что  и . Первое соответствует квазистатическому приближению, что справедливо в терагерцевой области частот. Второе условие используется для упрощения вычисления входящих в формулы функций Бесселя. В частности, при таком условии можно воспользоваться приближенным соотношением , . Кроме дисперсионного соотношения, из приведенных выше уравнений можно получить замкнутую систему уравнений для расчета вынужденных плазменных колебаний в Фурье пространстве:

                                    (4)                                                    

Здесь ,  и  - амплитуды Фурье-гармоник в -пространстве соответствующих функций ,  и . Заметим, что полем падающей волны длины  можно возбудить только симметричные моды плазменных колебаний. Принимая во внимание, что фазовая скорость плазменных волн  достаточно медленно меняется при изменении волнового вектора , можно переписать (4) в -пространстве:

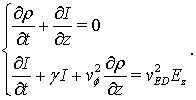                                                     (5)                                                           

Здесь  ‑ погонный заряд рассматриваемой системы из двух нанотрубок, и  ‑ электрический ток в них. Уравнения (5) должны решаться со следующими граничными условиями (разомкнутые концы):

                                           (6)                                                       

Из-за малого размера системы ( мкм), электрическое поле терагерцевой волны, падающей на нее, может считаться пространственно однородным, так что можно положить:  Это соответствует линейно поляризованной волне с электрическим вектором, колеблющимся вдоль нанотрубок. Решая уравнения (5) с граничными условиями (6), получаем:

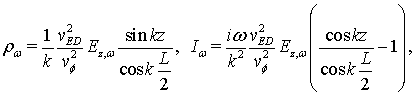           (7)                              

где  ‑ Фурье компонента функции ,  и  ‑ Фурье компоненты действительных функций  и  в -пространстве.

Выражения для  и  имеют полюсы, определяемые следующим образом:

                                                      (8)                                                            

действительные части  представляют собой резонансные частоты получившегося плазменного резонатора, мнимые части отвечают за затухание колебательных мод. Добротность плазменного резонатора  может быть определена как .

Механические колебания нанотрубок

В случае близкого расположения нанотрубок друг к другу, когда , распределенная сила отталкивания между ними ввиду наличия заряда  на каждой из них, может быть вычислена как  Если добротность основного резонанса плазменных колебаний достаточно велика () и Фурье спектр внешнего сигнала  в достаточно узкой области вблизи резонансной частоты , погонная сила  в  пространстве может быть выражения в следующем виде:

       (9)                             

где  ‑ величина линейной плотности заряда на правом конце системы.

Определив силу, действующую на нанотрубки, запишем уравнение ее механических колебаний:

          (10)                                  

где  ‑ смещение вдоль направления  оси нанотрубки относительно недеформированного состояния,  ‑ константа, определяющая затухание колебаний,  ‑ погонная масса нанотрубки,  ‑ ее жесткость на изгиб. Решение данного уравнения можно найти в следующем виде:

                                                     (11)                                                         

где  ‑ нормированные на 1 пространственные составляющие решений однородного уравнения (10) с правой частью равной нулю:

                                      (12)                                                      

где  ‑ комплексная частота свободных колебаний нанотрубок. Дисперсионное уравнение для  имеет следующий вид [9]:

                               (13)                                                 

Подставив разложение (11) в уравнение (10) и используя разложение функции  в ряд по функциям , образующим ортонормированный базис,

                     (14)                                            

получаем набор независимых уравнений для переменных амплитуд пространственных пространственных мод свободных колебаний:

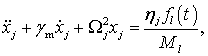                                                        (15)                                                            

где  ‑ резонансная частота, соответствующая данной функции , которая выражается следующим образом:

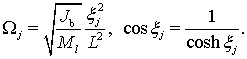                                                 (16)                                                      

Здесь, корни  дисперсионного уравнения нумеруются, начиная с , так что  и .

 

Уравнения для связанных мод механических и плазменных колебаний

В дальнейшем мы будем рассматривать такой входящий сигнал , спектр которого сосредоточен вблизи основного плазменного резонанса в нанотрубках  (см. уравнение (8)) и который имеет ширину порядка величины, равной частоте механического резонанса  (см. уравнение (16)). При таких условиях можно пренебречь более высокими гармониками плазменных и механических колебаний, и рассматривать возбуждение только основных. Согласно уравнениям (16) и (9) имеем:

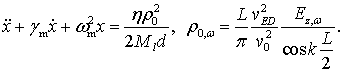                             (17)                                  

Здесь мы положили  и . Теперь соотношение между  и  записано в -пространстве, но если использовать приближение для выражения , которое справедливо когда ,

                 (18)                      

Можно переписать данное соотношение в -пространстве:

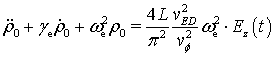        .                                  (19)                                                 

Далее, примем в рассмотрение то обстоятельство, что резонансная частота  меняется при деформировании нанотрубок. Чтобы вычислить смещение резонансной частоты при малых деформациях нанотрубок () требуется решать уравнения (5) с граничными условиями (6) при фазовой скорости плазменных волн, зависящей от координаты:

                                              (20)                                                    

где  вычисляется по формуле (3) для недеформированных нанотрубок. Легко показать, что по сравнению со случаем без деформации, когда условие плазменного резонанса есть , в случае малой деформации оно преобразуется в следующее:

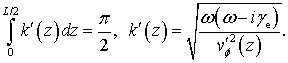                                         (21)                                              

Выполнив вычисления, получим выражение, определяющее положение смещенного резонанса :

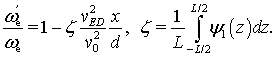                                             (22)                                                 

Подставляя  в уравнение (19) и выписав его вместе с уравнением (17) для механического резонатора, получаем следующую систему уравнений:

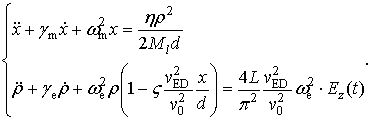                         (23)                             

Здесь для удобства мы опустили нижний индекс и положили .

Таким образом, при заданном внешнем сигнале  из уравнения (23), можно определить функции  и .

 

Возбуждение механических колебаний

В этом разделе рассмотрим случай модулированного сигнала входящего ТГц излучения:

                                                (24)                                                

где  ‑ амплитуда несущей волны, и  ‑ глубина модуляции. Решая уравнения (23) для такого , мы можем пренебречь зависимостью частоты плазменного резонанса в нанотрубках от их механической деформации. Это справедливо для данной задачи, поскольку этот сдвиг частоты достаточно мал даже при максимальной деформации нанотрубок, когда они начинают касаться друг друга. В этом случае  или  и при этом относительный частотный сдвиг , что меньше относительной ширины резонанса . Таким образом, мы можем считать, что механическое движение нанотрубок не влияет на плазменные колебания в них, и для  получить следующую формулу:

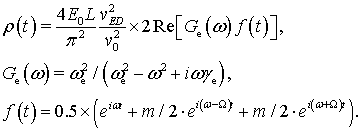                             (25)                              

Здесь было использовано приближение .

Подставив (25) в уравнение для механических колебаний (23), получаем следующее выражение для :

                     (26)             

В этом выражении для  опущены постоянный член и высокочастотные гармоники.

Чтобы проиллюстрировать эффективность возбуждения механических колебаний нанотрубок, рассмотрим схему для их детектирования, показанную на рис. 2. В этом устройстве две нанотрубки заряжаются от источника постоянного напряжения . В процессе механических колебаний электрический заряд на нанотрубках остается запертым и не течет по цепи источника постоянного напряжения из-за включенного в нее большого сопротивления . Величина этого сопротивления оценивается как  или  МОм, где  ‑ погонная емкость конденсатора, образованного двумя нанотрубками. При таких условиях, амплитуда перемнного напряжения на выходе детектора будет равна   (см. (22)).

 

 

 

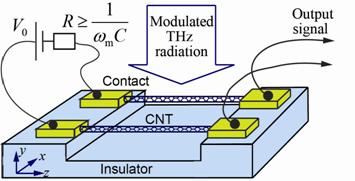
Рис. 2. Схема детектирования механических колебаний ОУНТ индуцированных модулированным терагерцевым излучением.

 

Чувствительность детектора  ‑ это отношение амплитуды сигнала на выходе  к общей мощности , поглощаемой устройством. Величина состоит из мощности  поглощаемой в электронной плазме в нанотрубках, мощности  затрачиваемой при механических колебаниях нанотрубок, и мощности переизлучения . В случае совместного плазменного и механического резонансов, когда  и , получается, что отношение  к  определяется следующей формулой:

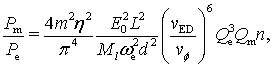                                                (27)                                              

где  и  ‑ добротности плазменного и механического резонаторов соответственно,  ‑ отношение резонансной частоты плазменного резонатора к частоте механического. Для нанотрубок длиной  мкм, их радиусе  нм и расстоянии между их осями  нм,     и  В/см (что соответствует интенсивности входящего излучения 1 мВт/см²) получаем:  см/с,  см/с,  ТГц, ,  ГГц, и отношение . Также, известно (см, например, работы [10, 11]), что эффективность (т.е. отношение ) антенн из углеродных нанотрубок в терагерцевой области имеет порядок . Таким образом, можно считать, что  и определить максимальную чувствительность детектирования  следующим образом:

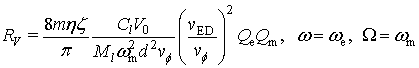                 (28)                     

Выполнив вычисления, для постоянного напряжения  Вольт, получаем  В/Вт.

 

Параметрическое возбуждение механических колебаний нанотрубок

Структура уравнений (23) допускает возбуждение механических колебаний в рассматриваемой системе, в том числе и при падении на нее монохроматического, немодулированного терагерцевого сигнала:

                                                           (29)                                                              

Поскольку плазменные колебания устанавливаются не мгновенно при изменении геометрии системы (ее деформации), член в правой части уравнения для механического осциллятора в системе (23) может быть представлен как сила, запаздывающая по времени:

                                                           (30)                                                             

где  ‑ время установления плазменных колебаний. Константа затухания колебаний  в уравнении (30) может получить отрицательную добавку, зависящую от амплитуды входящего сигнала. Для величин  выше определенного порогового значения  декремент затухания колебаний оказывается отрицательным, что соответствует генерации механических колебаний или самовозбуждению. Детальная процедура нахождения пороговых амплитуд входящего сигнала в подобных системах, описываемых уравнениями (23) представлена в работах [6, 7, 12]. Используя данные методы, можно для  получить следующую оценку:

                                                   (31)                                                     

Для параметров, указанных выше, получаем  кВ/см или  мВ на длину системы  мкм. Из теории антенн (см., например, работу [13]), данная величина электрического поля может быть получена в области фидера обыкновенной антенны (например, дипольного типа) при падении на нее терагерцевого излучения интенсивностью 1 Вт/см².

 

Заключение

В настоящей работе предложена и проанализирована модель, описывающая возбуждение связанных механических и плазменных колебаний в системе из двух параллельных ОУНТ, выполняющей роль антенны терагерцевого излучения. Оказалось, что такая антенна является детектором модулированного терагерцевого излучения, характеризующимся чувствительностью порядка  В/Вт, что является достаточно высоким значением. Немодулированное ТГц излучение также может вызывать возбуждение механических колебаний в системе. Однако, такое самовозбуждение системы из двух связанных осцилляторов может произойти только в интенсивных электромагнитных полях, для создания которых необходимо использовать усиливающие системы (антенны или линзы), способные увеличивать величину амплитуды входящей волны по крайней мере в несколько десятков раз.

Работа выполнена при частичной финансовой поддержке Министерства образования и науки Российской Федерации в рамках ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы» (контракт № 16.513.11.3129).

 

Литература

1.     M. Tonouchi, Cutting-edge terahertz technology // Nature Photonics 1 (2), 97 (2008).

2.     H.C. Nathanson, W.E. Newell, R.A. Wickstrom, J.R. Davis, The resonant gate transistor // IEEE trans. on Electron Devices 14, 117 (1967).

3.     V. Ryzhii, M. Ryzhii, Y. Hu, I. Hagiwara, M.S. Shur, Resonant detection of modulated terahertz radiation in micromachined high-electron-mobility transistor // Appl. Phys. Lett. 90, 203503 (2007).

4.     V.G. Leiman, M. Ryzhii, A. Satou, N. Ryabova, V. Ryzhii, T. Otsuji, and M.S. Shur, Analysis of resonant detection of terahertz radiation in high-electron mobility transistor with a nanostring/carbon nanotube as the mechanically floating gate // J. Appl. Phys. 104, 024514 (2008).

5.     Yu. Stebunov, V. Leiman, A. Arsenin, A. Gladun, V. Semenenko, V. Ryzhii, Detection of Modulated Terahertz Radiation Using Combined Plasma and Mechanical Resonances in Double-Carbon-Nanotube Device // Appl. Phys. Express 4, 075101 (2011).

6.     A.V. Arsenin, A.D. Gladun, V.G. Leiman, V.L. Semenenko, V.I. Ryzhii, Parametric instability in a nanoelectromechanical detector of modulated terahertz radiation on the basis of a high electron mobility transistor with a mobile elastic gate // J. Commun. Technol. Electron. 54 (11), 1322 (2009).

7.     A.V. Arsenin, A.D. Gladun, V.G. Leiman, V.L. Semenenko and V.I. Ryzhii, Parametric Instability in the Resonance Detector of Terahertz Radiation Based on FET with Cylindrical Gate Electrode // J. Commun. Technol. Electron. 56 (10), 1242 (2011).

8.     A. Maffucci, G. Miano, and F. Villone, A transmission line model for metallic carbon nanotube interconnects // Int. J. Circ. Theor. Appl. 1 (36), 31 (2008).

9.     L.D. Landau and E.M. Lifshitz, Theory of Elasticity, Pergamon, New York, 1986.

10.    G.V. Hanson, Fundamental Transmitting Properties of Carbon Nanotube Antennas // IEEE Trans. Antennas and Prop. 53 (11), 3426 (2005).

11.    M.V. Shuba, G.Ya. Slepyan, S.A. Maksimenko, C. Thomsen, A. Lakhtakia, Theory of multiwall carbon nanotubes as waveguides and antennas in the infrared and the visible regimes // Phys. Rev. B 79 (15), 155403 (2009).

12.    V.B. Braginsky, A.B. Manukin, Measurement of Weak Forces in Physics Experiments, U. Chicago Press, Chicago, III., 1977.

13.    R.S. Elliott, Antenna Theory and Design. Englewood Cliffs, NJ: Prentice-Hall, 1981.