УДК 621. 372. 852

РЕЗОНАНСНОЕ ДИФРАКЦИОННОЕ ПРЕОБРАЗОВАНИЕ ВОЛН В СТУПЕНЧАТО-НЕОДНОРОДНЫХ ОСЕСИММЕТРИЧНЫХ ДИЭЛЕКТРИЧЕСКИХ СТРУКТУРАХ

А. К. Малышкин, Ю. А. Пирогов

физический факультет МГУ имени М.В. Ломоносова,

кафедра фотоники и физики микроволн

Получена 14 июня 2012 г.

 

Аннотация. В миллиметровом диапазоне волн исследованы электродинамические характеристики осесимметричных диэлектрических стержней с периодически возмущенной поверхностью и шагом неоднородности, большим длины волны. Показано, что высокий коэффициент передачи волновой энергии в области резонансных максимумов на частотных спектрах систем определяется эффектом резонансного дифракционного преобразования волн на ступенчатых неоднородностях.

Ключевые слова: дифракционное преобразование волн, миллиметровый диапазон, сверхразмерные периодические структуры, осесимметричный диэлектрический стержень.

Abstract. Electrodynamic characteristics of axial symmetric dielectric bars with periodical disturbed surface and bigger wavelength step were investigated in millimeter wave range. It was shown that high wave energy transmission coefficient in resonance maxima on the frequency spectra of the systems is defined by resonance diffraction transformation of waves on step non-uniformities.

Keywords: diffraction wave transformation, millimeter waves, super-side periodical structure, axial symmetric dielectric bar.

Введение

Интерес к исследованию дифракционных характеристик периодических структур и неоднородностей волноводных трактов вызван рядом полезных эффектов, которые находят свое применение в конкретных приборах и устройствах миллиметровых волн - фильтрах, диплексерах, замедляющих структурах. К ним можно отнести эффекты преобразования волн в частично заполненных волноводах, в уголковых и ступенчатых волноводных неоднородностях, в соосных сочленениях круглых волноводов с  разным сечением. При этом существует возможность достижения полного или близкого к полному режима резонансного дифракционного преобразования одной волны в другую [1, 2].

Обычно рассматриваются периодические структуры с периодом, много меньшим или много большим длины волны, а случай неоднородностей, сравнимых с длиной волны, оказывается почти неизученным. Строгая теория таких систем требует чрезмерно большого вычислительного ресурса и потому их экспериментальное изучение представляется актуальным.

 Результаты измерений и анализ волн в исследованных образцах

В экспериментах, проведенных по методике [3, 4],  были экспериментально исследованы тефлоновые (e = 2,05) стержни диаметром d с крупноразмерной периодической структурой, представляющей собой цилиндрические секции с различными внешними диаметрами D (рис. 1). Стержни отличались также диаметром узкого участка d, его длиной и шагом периодики b, который выбирался из расчета b>l.

 

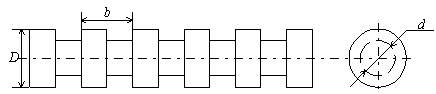
Рис. 1.  Исследуемая осесимметричная диэлектрическая структура.

Стержни возбуждались через боковую стенку секции меньшего диаметра d при помощи диэлектрического волновода 1 (рис. 2). Целью являлось возбуждение максимального количества секций по длине диэлектрического образца.

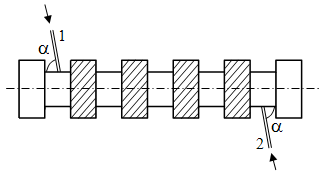
Рис. 2.  Схема поперечного возбуждения образца диэлектрическим волноводом.

 

В стремлении уменьшить потери энергии на излучение была применена частичная металлизация поверхности секций с диаметром D. Возбуждающий (1) и приемный (2) волноводы располагались в наклонном положении под углом a к структуре; оптимальный угол возбуждения a изменялся в пределах 80-90⁰ к продольной оси образца в зависимости от параметров структуры. Таким образом, оптимальные условия возбуждения колебаний в таких структурах соответствуют весьма малым углам отклонения (0-10⁰) волнового вектора  возбуждающей волны от нормали к структуре.

В диэлектрическом стержне с параметрами D = 16 мм, d = 8 мм, b = 18 мм эффективно возбуждались только две секции при оптимальном угле a_оптим.=89⁰. При этом коэффициент передачи А/А_вх достигал максимальной величины 0,86 на частоте f = 40,23 ГГц (рис. 3).

В диэлектрической структуре с D = 20 мм, d = 12 мм и шагом b = 18 мм возбуждались три секции при a_оптим. = 83⁰. В этом случае коэффициент передачи составил 0,77 на частоте f = 41,2 ГГц (рис. 4).

Важно отметить, что металлизация поверхности участков с малым диаметром d не привела к эффективному возбуждению структуры.

Рассмотрим причины, объясняющие высокий коэффициент передачи на графиках спектров (рис. 3, 4) для двух исследуемых структур.

 

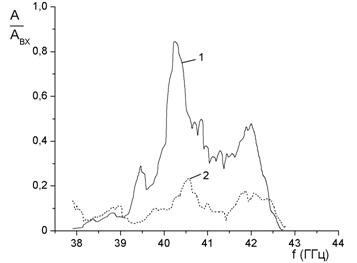
Рис. 3. Зависимость коэффициента передачи от частоты при возбуждении диэлектрического стержня с периодической структурой D = 16 мм, d = 8 мм, b = 18 мм: 1 – сигнал на выходе 2-ой секции; 2 – на выходе 3-й секции.

 

 

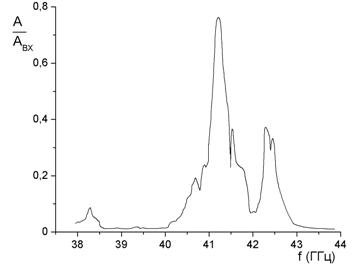
Рис. 4. Зависимость коэффициента передачи от частоты на выходе 3-й секции диэлектрического стержня  с периодической структурой D = 20 мм,        d = 12 мм, b = 18 мм.

 

Разумно полагать, что спектральные кривые на рис. 3 и 4 объясняются продольным резонансом одного из возбуждаемых в стержне нормальных колебаний на участках секций с большим диаметром, представляющих собой диэлектрический резонатор.

Характеристическое уравнение для волн круглого диэлектрического волновода имеет вид [5]:

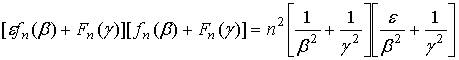,               (1)

где 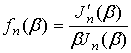, , 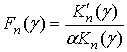– функция Бесселя, – функция Макдональда, а – радиус волновода, γ -  безразмерное "внешнее" волновое число; b - безразмерное "внутреннее" волновое число, n – азимутальный индекс волны, e - относительная диэлектрическая проницаемость.

Только в случае аксиальной симметрии (n = 0) возможно существование волн чисто электрического Е-типа и чисто магнитного Н-типа, что выражается в расщеплении уравнения (1) на ряд независимых уравнений.

При этом критические значения b_кр в случае симметричных Е- и Н-волн должны удовлетворять уравнению

J₀(b) = 0.                                                   (2)

Для волн типа HE_nm при n = 1 критические значения b_кр определяются решениями уравнения J₁(b_кр) = 0, причем для основной волны НЕ₁₁ следует принимать первый корень уравнения J₁(b_кр) = 0 равным нулю.

Для HE_nm волн с индексом n ³ 2 критические условия определяются корнями уравнения

                                         (3)

Волны типа EH_nm с любым индексом n критические условия определяются корнями уравнения

J_n(b_кр) = 0,                                                  (4)

при этом нулевой корень не удовлетворяет в этом случае характеристическому уравнению, так что волна ЕН₁₁ не существует.

Таким образом, корни характеристического уравнения b_кр определяют типы колебаний в соответствующих волноводах.

Расчет показал, что в диэлектрических волноводах с диаметрами d = 8 мм и D = 16 мм (для первого образца) могут возбуждаться 4 и 14 различных волн соответственно. Во втором образце с размерами d = 12 мм и D = 20 мм могут существовать соответственно 8 и 25 различных волн.

Для каждой из разрешенных мод был определен набор резонансных волн по числу полуволн, которые могут укладываться на длине диэлектрического резонатора с диаметром D. При этом оказалось, что все волны, попадающие в резонанс на участках секций с диаметром D, являются запредельными для волновода с диаметром d. Это означает, что распространяющиеся волны на широких участках периодической структуры не могут просочиться непосредственно через протяженный запредельный узкий участок. В таком случае проникновение волны из одного участка в другой можно объяснить дифракционным преобразованием мод на ступенчатых неоднородностях периодической структуры. Очевидно при этом, что в осесимметричных системах дифракционное преобразование должно осуществляться так, чтобы пространственные распределения электрических и магнитных волновых полей были подобными на обоих смежных участках структуры.

Еще в работе [6] отмечалось, что эффективное резонансное преобразование волн осуществляется в таких ступенчатых соединениях коаксиальных волноводов с параметрами q = d/D, у которых радиальное распределение поля некоторой i-й волны в узком волноводе (d) совпадает с частью вариации поля  k-й волны в широком (D). В этом случае i-я волна в узком волноводе становится распространяющейся одновременно с k-й волной широкого волновода, а для диаметров волноводов имеет место выражение

                                                  q = b_{кр i} /b_{кр k} .                                                 (5)

Проведенный для каждой нашей структуры расчет соотношения (5) определил ряд возможных преобразований волн, чьи радиальные распределения полей были подобными в смысле утверждения [6]. В свою очередь, анализ по методике [5] показал, что в радиальном направлении вариации волновых полей являются подобными для следующих основных (т.е. низшего из возможных порядка) комбинаций мод:

-  НЕ₂₁® НЕ₄₁ в случае первой структуры

-  НЕ₃₁® НЕ₅₁ в случае второй структуры.

 

  

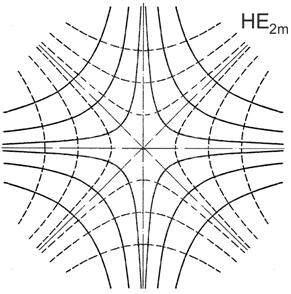
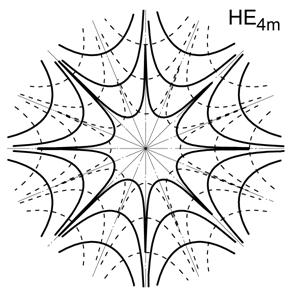
Рис. 5.  Картины поля волн НЕ_2m и НЕ_4m в поперечной плоскости круглого диэлектрического волновода.

 

 

   

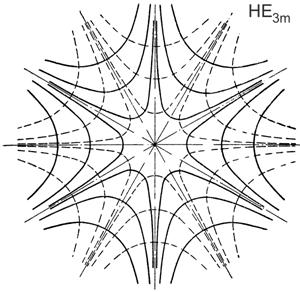
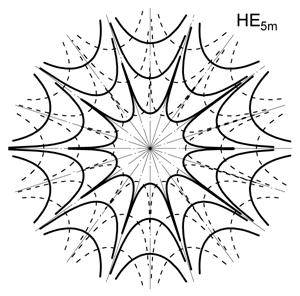
Рис. 6.  Картины поля волн НЕ_3m и НЕ_5m в поперечной плоскости круглого диэлектрического волновода.

 

При этом волны НЕ₄₁ и  НЕ₅₁ являются резонансными для диэлектрического резонатора с диаметром D, а волны НЕ₂₁ и НЕ₅₁ - распространяющимися на узких участках d.

На рис. 5 и 6 представлены картины полей соответствующих волн в поперечной плоскости круглого диэлектрического волновода. Электрические силовые линии в поперечной плоскости круглого диэлектрического волновода изображены на рисунках сплошными линиями. Магнитные силовые линии показаны на рисунке пунктирными линиями.

Необходимо отметить, что колебания НЕ₂₁ и НЕ₃₁ распространяются в волноводе с диаметром d вблизи его критического значения. При этом значительная часть поля этих волн находится вне волновода (d). Это хорошо объясняет факт, что при металлизации поверхности узких участков секций эффективного возбуждения структур получить не удается. С другой стороны, волны НЕ₄₁ и НЕ₅₁ далеки от критического режима в волноводе D. Более того, эти волны характеризуются преимущественно поперечным переносом энергии, так что металлизация волновода диаметра D создает дополнительные условия для эффективного преобразования волн и переноса энергии с минимальными потерями, что и имело место в эксперименте.

Описание второго резонансного максимума на спектрах рис. 3 и 4 сводится к аналогичной вышеуказанной цепочке расчетов уже при f = 42,0 ГГц и f = 42,4 ГГц соответственно. Однако значительно меньший коэффициент передачи в этих максимумах свидетельствует о невысокой эффективности соответствующих дифракционных преобразований.

Анализ спектра трехсекционной структуры с параметрами D = 16 мм, d = 8 мм, b = 18 мм (рис. 3 – кривая 2) показывает значительное уменьшение коэффициента передачи до 0,23 по сравнению с кривой 1 на том же рисунке, что связано с невыполнением резонансных условий дифракционного преобразования колебаний при такой геометрии системы.

 

 Выводы

Анализ волн в исследованных периодических коаксиальных системах с параметрами D_1,2 = (16; 20 мм), d_1,2 = (8; 12 мм), b_1,2 = (18; 18 мм) показал, что высокий коэффициент передачи, наблюдаемый в резонансных максимумах на частотных спектрах систем определяется эффектом резонансного дифракционного преобразования волн НЕ₂₁® НЕ₄₁ и НЕ₃₁® НЕ₅₁ на ступенчатых соединениях узкого и широкого участков диэлектрических  стержней соответственно. Возбуждение резонирующих запертых мод НЕ₄₁ и НЕ₅₁ на широких участках систем осуществляется посредством дифракционного преобразования соответствующих волн НЕ₂₁ и НЕ₃₁, распространяющихся на запредельных для более высоких мод участках периодической структуры диэлектрических стержней [7].

 

Литература

 

1. Колесников В.С., Моденов В.П., Пирогов Ю.А., Свешников А.Г.  Резонансная дифракция волны Н₀₁ на диэлектрической неоднородности в Н-плоскости волновода // Радиотехника и электроника. 1987. т.32. №9. С. 1841-1848.

2. Шестопалов В.П., Кириленко А.А., Рудь Л.А.  Резонансное рассеяние волн. Т.2 - Волноводные неоднородности. – Киев: Наукова Думка, 1985. 216 с.

3. Afonin D.G., Malyshkin A.K. Waveguide metallo-dielectrical structure // Proceedings Intern. AMSE Conf. “Signals and systems”, Geneva (Switzerland) June 17-19, 1992, AMSE Press. 1992. Vol.1. P. 255-265.

4.  Малышкин А.К., Пирогов Ю.А.  Резонансно-дифракционные преобразования волн в аксиально-симметричных неоднородных диэлектрических структурах // Препринт №3/2008 ЦМТС МГУ им. М.В. Ломоносова. 2008.  9 с.

5. Взятышев В.Ф.  Диэлектрические волноводы. – М.: Сов. радио, 1970. 216 с.

6. Шестопалов В.П., Кириленко А.А., Рудь Л.А.  Резонансное рассеяние волн. Т.2 - Волноводные неоднородности. – Киев: Наукова Думка, 1985. 216 с.

7.  Малышкин А.К. Автоматизированные исследования открытых электродинамических систем миллиметрового диапазона. Дисс. к.ф.-м.н.- М.: Физич. ф-т МГУ имени М.В. Ломоносова, 2009.