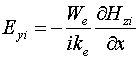УДК 621.396.67
РУПОРНЫЙ ОБЛУЧАТЕЛЬ ПЛАНАРНЫХ ЗЕРКАЛ И ЛИНЗ
С. Е. Банков 1, А. А. Курушин 2
1 ИРЭ им. В.А. Котельникова РАН, 2 НИУ МЭИ
Получена 7 июня 2013 г.
Аннотация. Рассматриваются вопросы моделирования и проектирования важного элемента интегральной микроволновой оптики – матричного облучателя. Исследуется решетка Е - плоскостных планарных рупоров, возбуждаемых двухсторонними щелевыми волноводами и решетка Н – плоскостных рупоров, возбуждаемых полосковыми линиями. Решетки анализируются в рамках моделей разного уровня: метод физической оптики, решение граничной задачи в приближении двумерной волноводной модели, решение трехмерной граничной задачи с помощью системы электродинамического моделирования FEKO. Рассматриваются решетки конечных размеров. Анализируются диаграммы направленности излучения рупоров в волны планарных волноводов. Исследуются эффекты, обусловленные конечными размерами решетки и длиной рупоров. Анализируются возможности корректного использования приближенной модели, построенной на основе метода физической оптики.
Ключевые слова: интегральная микроволновая оптика, планарный рупор, планарное зеркало, планарная линза, решетка планарных рупоров.
Abstract. Problems of modeling and design of an important element of integrated microwave optics – matrix radiator are considered. An array of E – plane planar horns excited by double-sided slot waveguides and array H – plane horns excited by microstrip lines are investigated. Arrays are analyzed in frames of models of different level: physical optics method, solution of boundary problem in approximation of two – dimensional waveguide model, solution of three – dimensional boundary problem with help of a system of electromagnetic modeling FEKO. Arrays of finite length are considered. Patterns of horn radiation in waves of planar waveguides are studied. Effects caused by array finite length and horn length are investigated. Tolerance of a model based on the physical optics method is analyzed.
Keywords: integral microwave optics, planar mirror, planar lens, planar horn, array of planar horns.
1. Постановка задачи
В последнее время в развитии техники миллиметрового и субмиллиметрового диапазонов (ММД и СММД) наблюдается устойчивая тенденция перехода от волноводных принципов формирования и пространственной обработки полей к оптическим принципам. Такая тенденция является продолжением наблюдавшейся ранее тенденции перехода от «проводного» механизма передачи электромагнитной энергии, связанного с использованием линий передачи с Т и квази – Т – волнами к волноводному механизму, связанному с использованием диэлектрических, металлических, щелевых, полосковых и т.д. волноводов [1]. Поскольку концентрация поля в волноводе существенно ниже, чем в линии передачи, то и затухание волн, в особенности обусловленное потерями в металлических элементах конструкции, в волноводах значительно меньше, чем в линиях передачи. Развивая эту идею дальше, можно отказаться от направляющих структур полностью и перейти к обработке и передаче волновых пучков, поле которых распределено в еще большей области пространства, чем в случае волновода. Основными элементами таких оптических или точнее квазиоптических устройств являются различные зеркала и линзы.
Указанная тенденция затронула не только объемные устройства, но и интегральные схемы, которые также могут строиться с использованием оптических принципов. В последние десятилетия был предложен ряд конструкций, линз [2], зеркал [3], резонаторов [4], фильтров [5], в основу которых положено преобразование двумерных волновых пучков, распространяющихся в, так называемых, планарных волноводах (ПЛВ). Чаще всего в качестве ПЛВ используются плоские волноводы (ПВ) в виде двух параллельных металлических экранов, пространство между которыми заполнено диэлектриком или планарные диэлектрические волноводы (ПЛДВ), представляющие собой диэлектрическую пластину с поверхностными волнами.
Устройства указного типа активно исследуются сейчас в связи с повышением актуальности технического освоения коротковолновой части ММД и СММД. Таким образом, можно говорить о появлении нового направления в данной области науки и техники, которое можно назвать планарной или интегральной СВЧ оптикой. Отметим, что наиболее вероятной областью практического использования обсуждаемых устройств является проектирование различных антенн ММД и СММД.
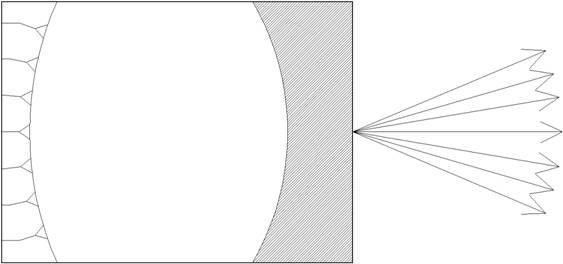
Как отмечалось выше, одними из наиболее важных элементов интегральной микроволновой оптики являются планарные зеркала и линзы [2,6]. Особенностью таких структур является то, что они осуществляют преобразование двумерных волновых пучков, которые распространяются в ПЛВ. Наиболее распространенным видом преобразования является трансформация пучка с цилиндрическим фазовым фронтом в пучок с плоским фронтом. На основе линз и зеркал, выполняющих такое преобразование, можно строить эффективные антенны, в том числе и многолучевые. Пример интегральной линзовой многолучевой антенны показан на рис. 1.
Рис. 1. Интегральная линзовая антенна
Проектирование таких антенн требует использования возбудителей, которые создают в ПЛВ пучок с цилиндрическим фазовым фронтом. Поэтому разработка возбудителей интегральных линз и зеркал является интересной и перспективной задачей. В традиционных зеркальных антеннах часто в качестве облучателя используется рупор, возбуждаемый металлическим волноводом [7]. Такие рупора хорошо согласованы и позволяют создавать диаграммы направленности (ДН) с шириной по уровню – 10 дБ в диапазоне 45-1200, которые обеспечивают оптимальные условия облучения оптической системы с большими электрическими размерами.
В данной работе исследуются планарные рупорные облучатели, предназначенные для формирования двумерных пучков, распространяющихся в ПЛВ. Пример такого рупора показан на рис. 2.
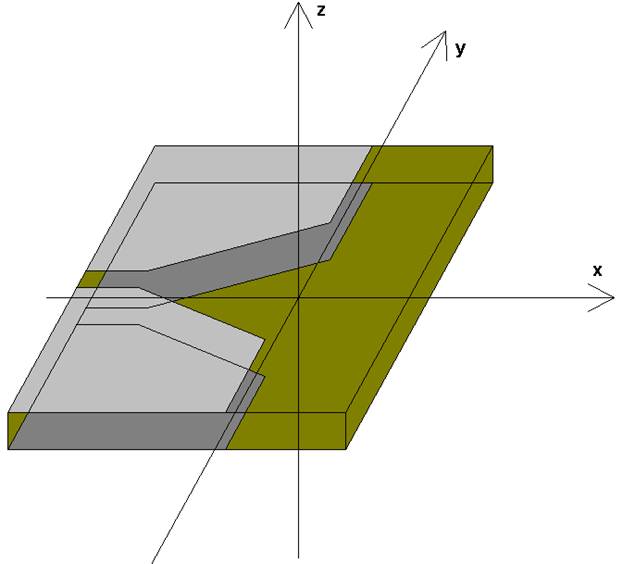
Рис. 2. Планарный Е – плоскостной рупор
Планарный рупор представляет собой печатную структуру на основе двухстороннего щелевого волновода (ДЩВ) [1]. Поперечное сечение ДЩВ представлено на рис. 3.
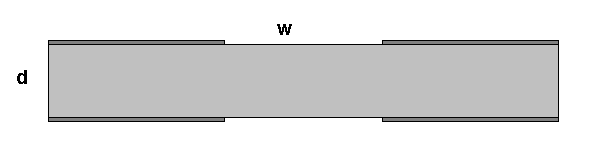
Рис. 3. Двусторонний щелевой волновод
Расширяясь, ДЩВ формирует планарный рупор. Отметим, что основная волна ДЩВ поляризована в плоскости диэлектрической подложки. Таким образом, расширение волновода происходит в плоскости вектора электрического поля. Поэтому планарный рупор данного вида можно назвать Е – плоскостным планарным рупором.
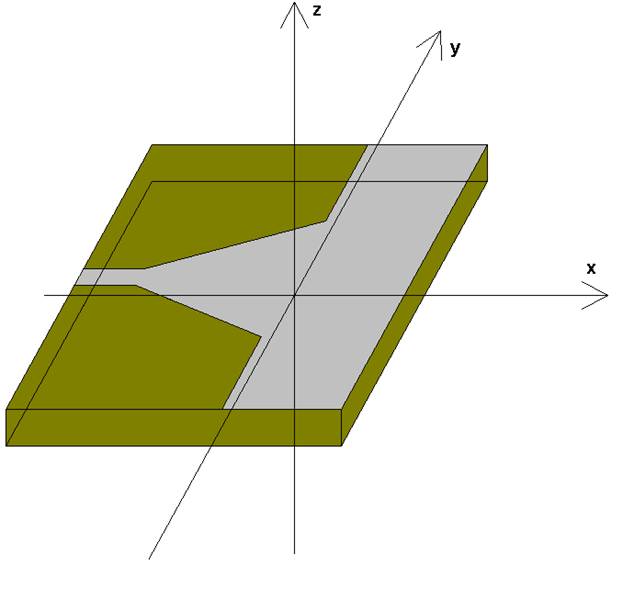
Рис. 4. Планарный Н – плоскостной рупор
Также распространены Н –
плоскостные рупора, возбуждаемые микрополосковыми линиями (МПЛ). Пример такого
рупора показан на рис. 4. Они излучают электромагнитное поле в ПВ,
расположенном в области ![]() . Обозначим толщину
подложки МПЛ через
. Обозначим толщину
подложки МПЛ через ![]() , а ширину линии через
, а ширину линии через ![]() .
.
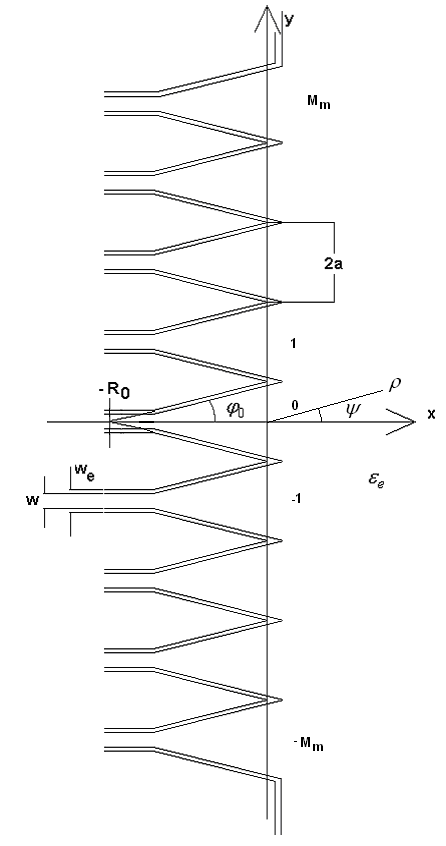
Матричный облучатель в интегральной СВЧ оптике, как правило, представляет собой решетку планарных рупоров, которые располагаются, как показано на рис. 5.
Рис. 5. Решетка планарных рупоров
На практике граница решетки бывает изогнутой вдоль некоторой кривой, которую принято называть дугой сканирования [8]. Ее форма определяется линзой или зеркалом, которое облучается решеткой (см. рис. 1). Электрический радиус кривизны дуги сканирования обычно весьма велик. Поэтому пренебрежение кривизной решетки и переход к структуре, показанной на рис. 5, оправданны.
Основной задачей
проектирования матричного облучателя является определение ДН его элементов. Для
этого необходимо решить сложную трехмерную электродинамическую граничную
задачу. Отметим, что в полном объеме, то есть с учетом всех рупоров,
формирующих облучатель, решить ее в настоящее время затруднительно. Причина
такого положения обусловлена сложностью структуры рассматриваемого устройства,
которое, с одной стороны, имеет электрические размеры много большие единицы. С
другой стороны, его функционирование определяют размеры сравнимые с длиной волны
или даже значительно меньшие ее. К их числу относится, например, толщина
подложки ![]() .
.
Большие размеры облучателя ставят ограничения на использование численных методов электродинамики, которые реализованы в таких системах как HFSS, MWS, FEKO. В тоже время, присутствие малоразмерных элементов не позволяет эффективно применять асимптотические методы решения граничных задач, которые используются при анализе трехмерных квазиоптических структур.
В такой ситуации наиболее эффективным оказывается комплексный подход, сочетающий различные приближенные методы со строгими методами численной электродинамики. Применение моделей разного уровня позволяет лучше прояснить природу процессов, происходящих в исследуемой структуре и выбрать приемлемый по точности и затратам способ их описания.
В данной работе используются следующие методы: наиболее простой метод физической оптики, более сложная модель, основанная на переходе от трехмерной структуры к двумерной и решении для нее двумерной граничной задачи, наиболее сложная модель, основанная на решении трехмерной граничной задачи для исходной структуры. Отметим, что переход к двумерной структуре является эвристическим этапом, который выполняется с помощью, так называемых, волноводных моделей ДЩВ и МПЛ [9].
Рассмотрим далее применение указанных методов для анализа матричного облучателя.
2. Волноводная модель решетки
На первом этапе рассмотрим переход от трехмерной граничной задачи к двумерной с помощью волноводных моделей ДЩВ и МПЛ. Отметим, что волноводную модель МПЛ также принято называть моделью Олинера. Переход к двумерным структурам является одним из ключевых этапов в двух методах (см. выше) из трех. Поэтому его целесообразно рассмотреть подробнее.
На рис. 6 представлены этапы
перехода от регулярных ДЩВ и МПЛ к их волноводным моделям в виде ПВ с шириной ![]() , заполненных средой с проницаемостью
, заполненных средой с проницаемостью ![]() . Параметры
. Параметры ![]() и
и ![]() рассчитываются на основе исходных
параметров волноводов
рассчитываются на основе исходных
параметров волноводов ![]() по известным алгоритмам [9],
[10]. Модели для МПЛ и ДЩВ отличаются только поляризацией волн и граничными
условиями на их стенках. Известно, что с помощью принципа Бабине [11] можно
перейти от волновода с магнитными стенками к волноводу с электрическими
стенками. Поэтому далее мы можем рассматривать одну модель, например, модель
ДЩВ, имея ввиду, возможность использования полученных результатов для модели
МПЛ.
по известным алгоритмам [9],
[10]. Модели для МПЛ и ДЩВ отличаются только поляризацией волн и граничными
условиями на их стенках. Известно, что с помощью принципа Бабине [11] можно
перейти от волновода с магнитными стенками к волноводу с электрическими
стенками. Поэтому далее мы можем рассматривать одну модель, например, модель
ДЩВ, имея ввиду, возможность использования полученных результатов для модели
МПЛ.
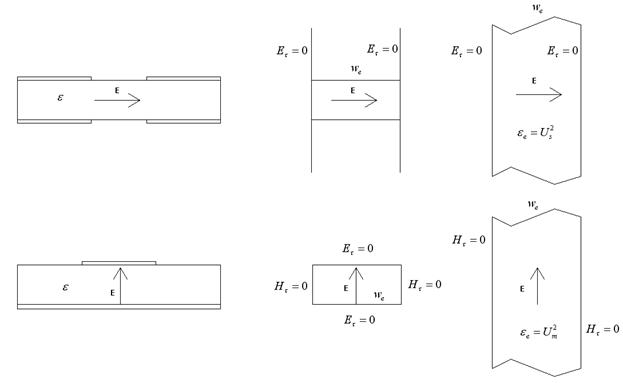
Рис. 6. Переход от трехмерных к двумерным структурам
Переход от трехмерной структуры к двумерной возможен не только для регулярного волновода, но и для более сложных структур, в том числе и для анализируемой решетки.
На рис. 6 показаны два контура. Правый
контур соответствует границам полосковых проводников в исходной трехмерной
структуре. Левый контур показывает двумерную структуру, образованную стенками,
параллельными оси 0z.
Полагаем, что это идеально проводящие стенки. Стенки сдвинуты относительно
границ проводников на расстояние ![]() :
:
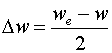 . (1)
. (1)
Нетрудно заметить, что при
переходе от двумерной решетки к трехмерной ее период равный ширине раскрыва
рупора ![]() остается неизменным. Происходит только
смещение модельной решетки по оси 0х, что необходимо учитывать при определении
места положения фазового центра ДН облучателя.
остается неизменным. Происходит только
смещение модельной решетки по оси 0х, что необходимо учитывать при определении
места положения фазового центра ДН облучателя.
Пространство между стенками,
а также в области ![]() заполнено диэлектриком с
проницаемостью
заполнено диэлектриком с
проницаемостью ![]() . В случае щелевой структуры она
равна
. В случае щелевой структуры она
равна ![]() , а в случае полосковой структуры она
совпадает с проницаемостью подложки МПЛ
, а в случае полосковой структуры она
совпадает с проницаемостью подложки МПЛ ![]() .
Параметр
.
Параметр ![]() - это коэффициент замедления
- это коэффициент замедления ![]() - волны диэлектрической пластины толщиной
- волны диэлектрической пластины толщиной
![]() и проницаемостью
и проницаемостью ![]() .
Строго говоря, эффективная проницаемость среды внутри модели решетки
.
Строго говоря, эффективная проницаемость среды внутри модели решетки ![]() должна меняться. Внутри каналов,
расположенных в области
должна меняться. Внутри каналов,
расположенных в области ![]() она не равна
проницаемости в области
она не равна
проницаемости в области ![]() . Однако численные
расчеты показывают, что это отличие весьма мало. Поэтому, учитывая изначально
приближенный характер волноводной модели, мы пренебрегали данным отличием.
. Однако численные
расчеты показывают, что это отличие весьма мало. Поэтому, учитывая изначально
приближенный характер волноводной модели, мы пренебрегали данным отличием.
3. Анализ решетки в приближении физической оптики
Из разд. 2 видно, что применение волноводной модели сводит исходную трехмерную задачу к задаче об излучении из решетки Е – плоскостных рупоров. Напомним, что решение для решетки Н – плоскостных рупоров получается из решения указанной выше задачи автоматически.
Пусть возбуждается
центральный канал решетки с номером ![]() . Назовем его активным
каналом. В качестве источника возбуждения рассматриваем основную волну ПВ,
которая бежит по нему слева направо. Основной волной ПВ является Т – волна. На
стыке с рупором она преобразуется в его основную волну, которую также называют
рупорной волной. Стык ПВ и рупора является нерегулярностью, которая вызывает
отражение и преобразование волн в другие типы. Будем полагать, что ПВ
одноволновый и распространяющиеся высшие типы волн в нем отсутствуют. Данное
условие исключает эффект преобразования волн. Отражение волн ПВ от стыка с
рупором также не будем учитывать, полагая, что влияние этого эффекта
незначительно. Данное предположение справедливо для рупоров с достаточно малым
углом раскрыва
. Назовем его активным
каналом. В качестве источника возбуждения рассматриваем основную волну ПВ,
которая бежит по нему слева направо. Основной волной ПВ является Т – волна. На
стыке с рупором она преобразуется в его основную волну, которую также называют
рупорной волной. Стык ПВ и рупора является нерегулярностью, которая вызывает
отражение и преобразование волн в другие типы. Будем полагать, что ПВ
одноволновый и распространяющиеся высшие типы волн в нем отсутствуют. Данное
условие исключает эффект преобразования волн. Отражение волн ПВ от стыка с
рупором также не будем учитывать, полагая, что влияние этого эффекта
незначительно. Данное предположение справедливо для рупоров с достаточно малым
углом раскрыва ![]() .
.
Таким образом, вся энергия Т
– волны ПВ переходит в основную волну рупора. Компонента ее поля ![]() записывается следующим образом:
записывается следующим образом:
![]() ,
,
![]() ,
,
где ![]() -
волновое число свободного пространства,
-
волновое число свободного пространства, ![]() - функция Ганкеля второго рода
нулевого порядка.
- функция Ганкеля второго рода
нулевого порядка.
Нас также будет интересовать
компонента электрического поля ![]() , связанная с
компонентой
, связанная с
компонентой ![]() через уравнения Максвелла [12]:
через уравнения Максвелла [12]:
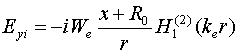 ,
,
где ![]() -
волновое сопротивление среды с проницаемостью
-
волновое сопротивление среды с проницаемостью ![]() .
.
Метод физической оптики
позволяет найти поле излучения в пространстве при ![]() , если
известно поле в плоскости
, если
известно поле в плоскости ![]() . Обычно при расчете
рупорных антенн его приближенно полагают равным полю набегающей волны. В нашем
случае это означает, что поле при
. Обычно при расчете
рупорных антенн его приближенно полагают равным полю набегающей волны. В нашем
случае это означает, что поле при ![]() определяется
соотношениями (2) и (3), а при
определяется
соотношениями (2) и (3), а при ![]() оно равно нулю.
оно равно нулю.
Заменим далее заданное на
плоскости ![]() поле эквивалентными электрическими и
магнитными токами
поле эквивалентными электрическими и
магнитными токами ![]() :
:
![]() ,
, ![]() . (4)
. (4)
Решение задачи о возбуждении
токами (4) однородного пространства позволяет найти искомое поле излучения и
его ДН. Для этого целесообразно воспользоваться выражением для функции Грина
однородного пространства ![]() [12], с помощью
которого можно записать выражение для компоненты поля излучения
[12], с помощью
которого можно записать выражение для компоненты поля излучения ![]() :
:
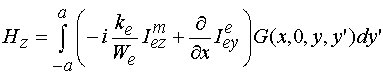 . (5)
. (5)
Поле в дальней зоне удобно
представлять в цилиндрической системе координат ![]() (см.
рис. 5). При
(см.
рис. 5). При ![]() функция Грина записывается следующим
образом:
функция Грина записывается следующим
образом:
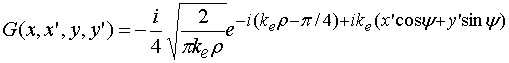 , (6)
, (6)
![]() .
.
С помощью соотношения (6)
можно найти ДН облучателя ![]() . Будем далее
использовать нормированную ДН. В качестве нормирующего множителя используем
значение ДН при
. Будем далее
использовать нормированную ДН. В качестве нормирующего множителя используем
значение ДН при ![]() :
:
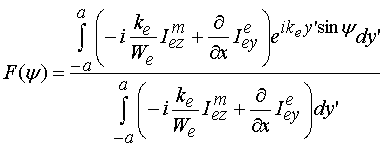 . (7)
. (7)
Интегралы в соотношении (7)
аналитически не берутся, но их легко определить численно. В приближении
длинного рупора, когда его угол раскрыва ![]() ,
выражения (2), (3) можно упростить, заменив функции Ганкеля асимптотическими
разложениями. Если также приближенно положить, что
,
выражения (2), (3) можно упростить, заменив функции Ганкеля асимптотическими
разложениями. Если также приближенно положить, что
![]() ,
,
то формула (7) приобретает вид:
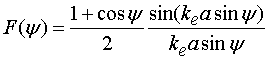 . (8)
. (8)
Видно, что в рамках простейшей модели описанной в разд. 3 ДН элемента решетки не отличается от ДН одиночного рупора и она также не зависит от положения рупора в решетке.
4. Электродинамическая модель двумерной решетки
В данном разделе будет построена модель решетки, содержащей конечное число рупоров. Модель основана на приближенном решении граничной задачи. Остановимся на принятых допущениях. К ним относятся пренебрежение отражением волн на стыках ПВ и рупоров и приближение длинных рупоров, которые уже обсуждались в разд. 3.
Приближение длинных рупоров
позволяет существенно упростить запись электромагнитного поля в области ![]() , а также вывод интегральных уравнений, к
которым сводится исходная граничная задача. В этом приближении поле внутри
рупора записывается следующим образом:
, а также вывод интегральных уравнений, к
которым сводится исходная граничная задача. В этом приближении поле внутри
рупора записывается следующим образом:
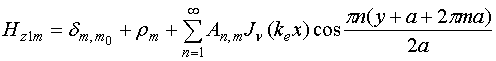 ,
(9)
,
(9)
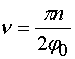 ,
,
где ![]() - функция Бесселя,
- функция Бесселя, ![]() -
символ Кронекера.
Коэффициент
-
символ Кронекера.
Коэффициент ![]() имеет смысл коэффициента отражения
основной волны в канале с номером
имеет смысл коэффициента отражения
основной волны в канале с номером ![]() ,
, ![]() ,
, ![]() -
общее число рупоров в решетке. Отметим, что структура анализируется при условии возбуждения одного
канала с номером
-
общее число рупоров в решетке. Отметим, что структура анализируется при условии возбуждения одного
канала с номером ![]() основной волной ПВ. Индекс 1 в формуле (9) соответствует
полю при
основной волной ПВ. Индекс 1 в формуле (9) соответствует
полю при ![]() . Коэффициенты
. Коэффициенты ![]() имеют смысл амплитуд
волн высших типов в рупорах. Мы предположили в разд. 3, что входные ПВ
одноволновые. Поэтому можно допустить, что поле высших типов рупорных волн не
проникает в ПВ и его искажением на стыке рупора и ПВ можно пренебречь.
имеют смысл амплитуд
волн высших типов в рупорах. Мы предположили в разд. 3, что входные ПВ
одноволновые. Поэтому можно допустить, что поле высших типов рупорных волн не
проникает в ПВ и его искажением на стыке рупора и ПВ можно пренебречь.
Формула (9) верна при выполнении следующих соотношений:
![]() ,
, 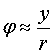 .
(10)
.
(10)
Они соответствуют
приближению длинных рупоров и позволяют заменить переменные ![]() , которые исходно присутствуют в
представлении поля переменными
, которые исходно присутствуют в
представлении поля переменными ![]() , которые используются
в (9).
, которые используются
в (9).
Магнитное поле в области 2,
расположенной при ![]() записывается в виде интеграла Фурье:
записывается в виде интеграла Фурье:
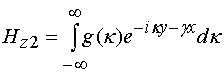 ,
(11)
,
(11)
![]() ,
,
где ![]() -
неизвестная спектральная плотность.
-
неизвестная спектральная плотность.
Дальнейший вывод
интегральных уравнений проводится стандартным образом. Поля в обеих областях
выражаются через электрическое поле в плоскости ![]() . Мы
предполагаем, в этой плоскости за пределами решетки имеются бесконечные фланцы.
Тогда компонента поля
. Мы
предполагаем, в этой плоскости за пределами решетки имеются бесконечные фланцы.
Тогда компонента поля ![]() отлична от нуля только в
раскрывах рупоров. Ее можно представить в виде множества функций
отлична от нуля только в
раскрывах рупоров. Ее можно представить в виде множества функций ![]() , каждая из которых описывает поле в
раскрыве рупора с номером
, каждая из которых описывает поле в
раскрыве рупора с номером ![]() . Выражая электрическое
поле в областях 1 и 2 через функции
. Выражая электрическое
поле в областях 1 и 2 через функции ![]() мы автоматически
удовлетворяем граничному условию непрерывности электрического поля в плоскости
мы автоматически
удовлетворяем граничному условию непрерывности электрического поля в плоскости ![]() . На следующем этапе через функции
. На следующем этапе через функции ![]() выражается магнитное поле в областях 1 и
2. Затем они приравниваются при
выражается магнитное поле в областях 1 и
2. Затем они приравниваются при ![]() . Равенство магнитных
полей дает нам искомую систему интегральных уравнений относительно
. Равенство магнитных
полей дает нам искомую систему интегральных уравнений относительно ![]() , решение которой позволяет удовлетворить
всем граничным условиям задачи.
, решение которой позволяет удовлетворить
всем граничным условиям задачи.
Приводим без вывода окончательный вид системы интегральных уравнений:
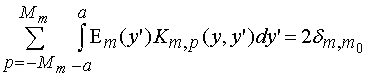 ,
,
![]() , (12)
, (12)
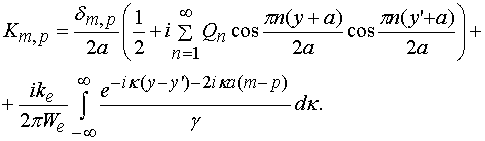
Решение системы (12) проводим
стандартным для таких задач методом Галеркина, представляя неизвестные функции в
виде ряда по базисным функциям ![]() :
:
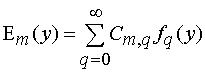 , (13)
, (13)
где ![]() - неизвестные
коэффициенты разложения (13).
- неизвестные
коэффициенты разложения (13).
Соотношение (13) подставляем
в систему (12) и проецируем ее на систему тестовых функций, совпадающих с
базисными. В результате мы получаем систему линейных алгебраических уравнений
(СЛАУ) относительно коэффициентов ![]() :
:
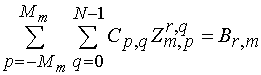 ,
,![]() ,
,![]() ,
,
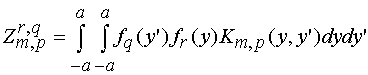 , (14)
, (14)
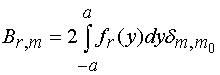 .
.
Параметр ![]() -
число базисных функций, используемых для описания поля, выбирается из условия
сходимости решения СЛАУ (14).
-
число базисных функций, используемых для описания поля, выбирается из условия
сходимости решения СЛАУ (14).
Введем следующие обозначения:
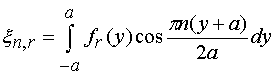 , (15)
, (15)
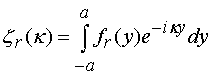 .
.
С их помощью внешние
параметры решетки выражаются через коэффициенты ![]() :
:
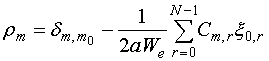 , (16)
, (16)
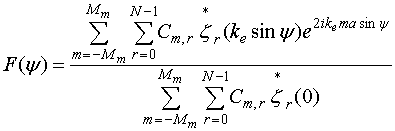 . (17)
. (17)
5. Электродинамическая модель трехмерной решетки
Электродинамическое моделирование решетки проводилось в системе FEKO [13]. Выбор FEKO в качестве инструмента моделирования решетки определялся возможностью, которую представляет метод интегральных уравнений, используемый в этой системе для решения граничных задач.
В отличие от других численных методов, которые применяются в системах HFSS и MWS метод интегральных уравнений необязательно требует ограниченных размеров области, в которой ищется поле. В частности, допустимо использовать модель решетки с бесконечной подложкой. При этом ограниченные размеры должны иметь только металлические проводники, нанесенные на ее поверхности.
Нетрудно видеть, что в класс указанных выше структур при определенных допущениях попадает решетка на основе Е – плоскостных рупоров и не попадает решетка Н – плоскостных рупоров. Решетка Е – плоскостных рупоров легко может быть преобразована к требуемому виду, если из нее удалить бесконечные фланцы (см. рис. 5). При этом бесконечная область, в которую происходит излучение поля, формируется диэлектрической подложкой свободной от проводников.
Иная ситуация в случае с полосковой решеткой. Здесь область, в которую излучает решетка, образована ПВ. Она имеет металлические проводники, уходящие на бесконечность. Ее также можно было бы свести к требуемому виду, если использовать в качестве неизвестных функций, относительно которых записываются интегральные уравнения, магнитные токи. Однако, в системе FEKO пока такая возможность отсутствует. Поэтому применение модели с бесконечной подложкой для полосковой структуры невозможно.
При этом необходимо отметить, что возможность моделирования бесконечных планарных структур в нашем случае является критически важной. Дело в том, что, ограничивая размеры подложки, мы вносим в структуру источник отражений, которые не позволяют рассматривать найденное поле как поле в дальней зоне, поскольку к нему добавляется поле, отраженное от границ подложки. Данное обстоятельство не позволяет использовать для анализа матричного облучателя такие системы как HFSS.
Возможно, что анализ полоскового облучателя следует проводить с помощью системы ADS, которая работает не только с электрическими, но и с магнитными токами. Однако, ее применение лежит за пределами возможностей авторов данной работы.
Таким образом, практически единственной структурой доступной численному анализу является матричный облучатель на основе ДЩВ. Следует отметить, что качественно полосковый облучатель не должен существенно отличаться от дуального аналога на ДЩВ по соображениям изложенным выше. Поэтому мы ограничились исследованием щелевой структуры.
Исследовались одиночные рупора и
решетки рупоров. После решения граничной задачи находилось поле на дуге
достаточно большого электрического радиуса с центром в начале координат. Дуга
лежит в плоскости XOY.
Это поле можно считать дальним и по его зависимости от угла ![]() можно найти ДН облучателя.
можно найти ДН облучателя.
Каналы облучателя в ходе численных расчетов были нагружены на сосредоточенные порты, импедансы которых определялись численно из условия наилучшего согласования. Для определения параметров портов была проанализирована отдельная структура в виде отрезка ДЩВ нагруженного с двух сторон указанными портами. Их импедансы находились по критерию минимума коэффициента отражения в полосе частот.
6. Численные результаты
Был проведен цикл численных
исследований матричных облучателей диапазона 30 – 40 ГГц, которые выполнялись
на подложке с проницаемостью ![]() толщиной
толщиной ![]() . Расчеты выполнялись с помощью трех
описанных выше моделей. Облучатель имел следующие параметры: число рупоров
. Расчеты выполнялись с помощью трех
описанных выше моделей. Облучатель имел следующие параметры: число рупоров ![]() , длина рупора
, длина рупора ![]() ,
ширина ДЩВ
,
ширина ДЩВ ![]() . Ширина раскрыва рупора
. Ширина раскрыва рупора ![]() изменялась в диапазоне 2 – 3.5.
Возбуждался центральный канал облучателя.
изменялась в диапазоне 2 – 3.5.
Возбуждался центральный канал облучателя.
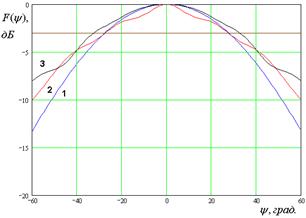
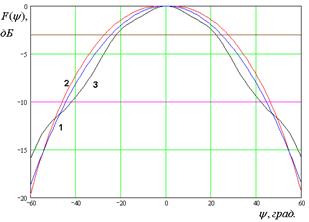
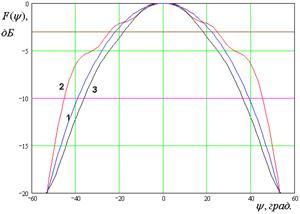
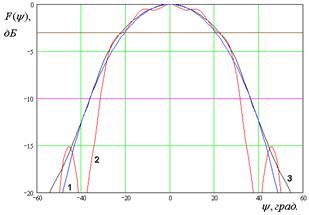
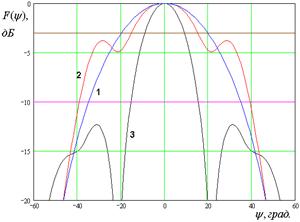
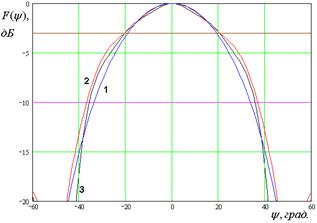
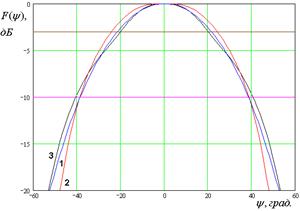
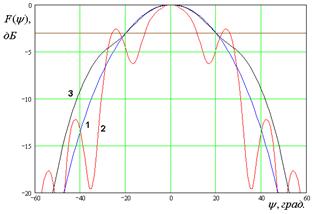
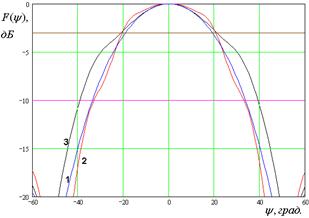
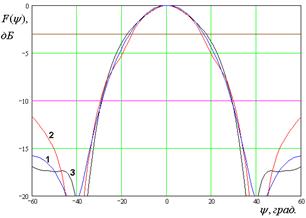
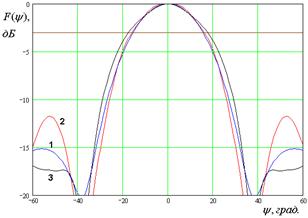
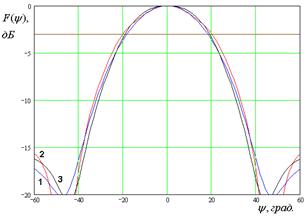
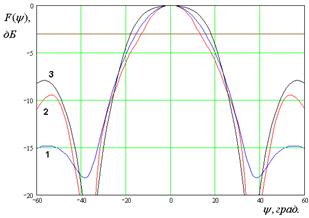
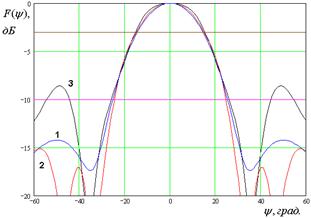
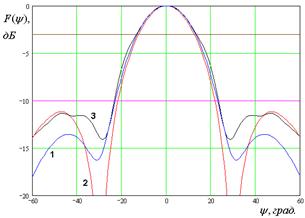
На рис. 7 – 10 представлены рассчитанные ДН.
Кривые 1 – 3 на рис. 7 –
10 соответствуют методу физической оптики, решению двумерной граничной дачи и
решению трехмерной граничной задачи. Рис. 7 а – е получены для ![]() ГГц. Рис. 8 а – д получены для
ГГц. Рис. 8 а – д получены для ![]() ГГц. Рис. 9 а – г получены для
ГГц. Рис. 9 а – г получены для ![]() ГГц. Рис. 10 а – г получены для
ГГц. Рис. 10 а – г получены для ![]() ГГц. Горизонтальными линиями на рис. 7 –
10 показаны уровни в – 3 и – 10 дБ, которые используются в антенной технике для
определения ширины ДН.
ГГц. Горизонтальными линиями на рис. 7 –
10 показаны уровни в – 3 и – 10 дБ, которые используются в антенной технике для
определения ширины ДН.
а б
в г
д е
Рис. 7. ДН облучателя при ![]()
а б
в г
д
Рис. 8. ДН облучателя при ![]()
а б
в д
Рис. 9. ДН облучателя при ![]()
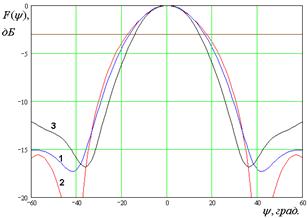
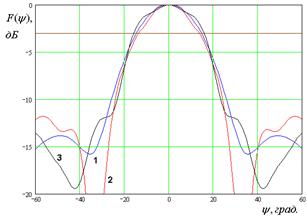
а б
в г
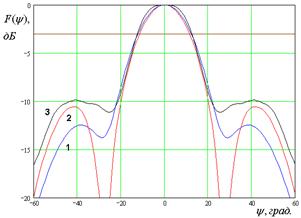
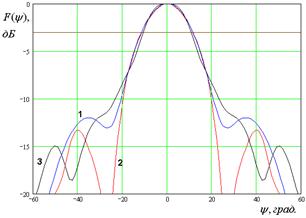
Рис. 10. ДН облучателя при ![]()
Анализ ДН, рассчитанных
тремя разными методами, позволяет сделать следующие выводы. Существует диапазон
частот, в котором результаты всех методов достаточно близки. При этом
совпадение улучшается при увеличении раскрыва рупора ![]() .
Однако, существуют относительно узкие диапазоны частот, в которых ДН,
полученные из решения двумерной и трехмерной задач ведут себя аномальным
образом: резко меняется ширина ДН, ее форма и уровень боковых лепестков. При
этом метод физической оптики не позволяет описать аномальное поведение ДН в
указанном диапазоне частот.
.
Однако, существуют относительно узкие диапазоны частот, в которых ДН,
полученные из решения двумерной и трехмерной задач ведут себя аномальным
образом: резко меняется ширина ДН, ее форма и уровень боковых лепестков. При
этом метод физической оптики не позволяет описать аномальное поведение ДН в
указанном диапазоне частот.
Таким образом, можно говорить
о существовании некоторого резонансного эффекта, который искажает форму ДН
облучателя. Его резонансная частота ![]() зависит от параметров
рупора. Так при
зависит от параметров
рупора. Так при ![]() она равна 39 ГГц, при
она равна 39 ГГц, при ![]() 33 ГГц, при
33 ГГц, при ![]() резонанс
слабо выражен и наблюдается на частоте 35 ГГц и при
резонанс
слабо выражен и наблюдается на частоте 35 ГГц и при ![]() резонансный
эффект не обнаружен.
резонансный
эффект не обнаружен.
Следует отметить следующее. Резонансная частота достаточно хорошо предсказывается с помощью двумерной модели, которая также хорошо описывает ДН в нерезонансной области, по крайней мере, в пределах главного лепестка. В окрестности резонанса данные, получаемые с помощью двумерной и трехмерной моделей, могут сильно отличаться. Тем не менее, обе модели предсказывают сильные искажения ДН, которые говорят о том, что облучатель в этой области частот неработоспособен. Поэтому вопрос о достоверности расчетов в ней не очень актуален. Важно лишь правильно предсказать частоту резонанса и полосу частот, в которой сильно его влияние.
Интересно выяснить природу
наблюдаемых резонансных эффектов. Для этого полезно исследовать частотные
зависимости коэффициентов ![]() , которые
рассчитываются в рамках двумерной модели решетки. Поле внутри рупора
складывается из поля основной распространяющейся волны, которой соответствует
номер
, которые
рассчитываются в рамках двумерной модели решетки. Поле внутри рупора
складывается из поля основной распространяющейся волны, которой соответствует
номер ![]() и высших типов волн с
и высших типов волн с ![]() . Высшие типы волн не проникают в
волновод. Они полностью отражаются от критического сечения рупора, в котором
они испытывают отсечку. Если раскрыв рупора также сильно отражает какую-нибудь
волну высшего типа, то для нее создаются условия для возникновения резонанса,
который иногда называют резонансом «запертых» мод. О наличии такого резонанса
будет свидетельствовать резкий рост одного из коэффициентов
. Высшие типы волн не проникают в
волновод. Они полностью отражаются от критического сечения рупора, в котором
они испытывают отсечку. Если раскрыв рупора также сильно отражает какую-нибудь
волну высшего типа, то для нее создаются условия для возникновения резонанса,
который иногда называют резонансом «запертых» мод. О наличии такого резонанса
будет свидетельствовать резкий рост одного из коэффициентов ![]() , которые имеют смысл амплитуд высших
типов волн.
, которые имеют смысл амплитуд высших
типов волн.
Будем анализировать вместо
коэффициентов ![]() коэффициенты
коэффициенты ![]() :
:
![]() , (18)
, (18)
где ![]() -
производная от функции Бесселя. Параметры
-
производная от функции Бесселя. Параметры ![]() имеют
смысл амплитуд электрического поля высших типов волн в раскрыве рупора.
имеют
смысл амплитуд электрического поля высших типов волн в раскрыве рупора.
а
б
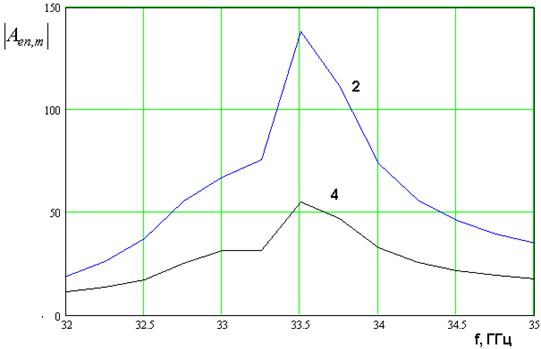
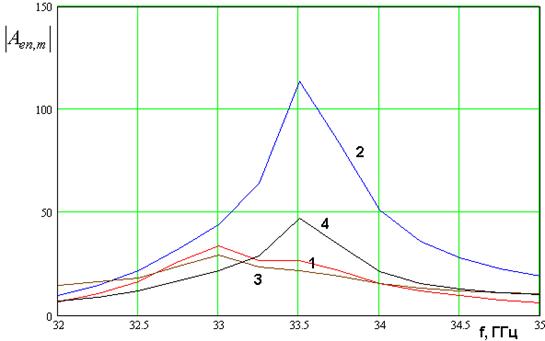
Рис. 11.
Частотные зависимости модулей параметров ![]()
На рис. 1 а,б показаны
частотные зависимости модулей коэффициентов ![]() .
Кривые 1 – 4 соответствуют номерам волн
.
Кривые 1 – 4 соответствуют номерам волн ![]() .
Кривые на рис. 11 а получены для центрального канала с
.
Кривые на рис. 11 а получены для центрального канала с ![]() ,
а кривые на рис. 11 б для канала с
,
а кривые на рис. 11 б для канала с ![]() при
при ![]() . Остальные параметры остались без
изменения.
. Остальные параметры остались без
изменения.
Видно, что коэффициенты ![]() ведут себя резонансным образом, достигая
максимума на частоте
ведут себя резонансным образом, достигая
максимума на частоте ![]() ГГц, которая близка к
резонансной частоте определенной выше по искажениям ДН. В центральном канале в
силу симметрии структуры волны с нечетными номерами не возбуждаются. В первом
боковом канале все амплитуды имеют конечные значения. Наибольшей из них
является амплитуда второй волны. Можно предположить, что ее резонанс является
источником аномального поведения решетки вблизи частоты
ГГц, которая близка к
резонансной частоте определенной выше по искажениям ДН. В центральном канале в
силу симметрии структуры волны с нечетными номерами не возбуждаются. В первом
боковом канале все амплитуды имеют конечные значения. Наибольшей из них
является амплитуда второй волны. Можно предположить, что ее резонанс является
источником аномального поведения решетки вблизи частоты ![]() ГГц.
ГГц.
На рис. 12 показана
частотная зависимость модуля коэффициента ![]() .
Кривые 1 – 4 получены для разных углов раскрыва рупора
.
Кривые 1 – 4 получены для разных углов раскрыва рупора ![]() при
при
![]() .
.
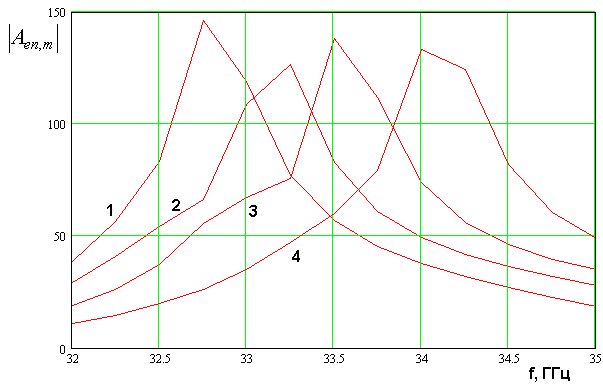
Рис. 12. Частотная зависимость модуля
параметра ![]()
Видно, что уменьшение угла раскрыва, то есть удлинение рупора снижает резонансную частоту.
Интересно, что резонанс в
решетке приводит к всплеску коэффициентов отражения в ее каналах по основной
волне ![]() . На рис. 13 показана частотная
зависимость модулей
. На рис. 13 показана частотная
зависимость модулей ![]() . Кривые 1 – 3 получены для
. Кривые 1 – 3 получены для ![]() . Параметры решетки приведены выше.
. Параметры решетки приведены выше.
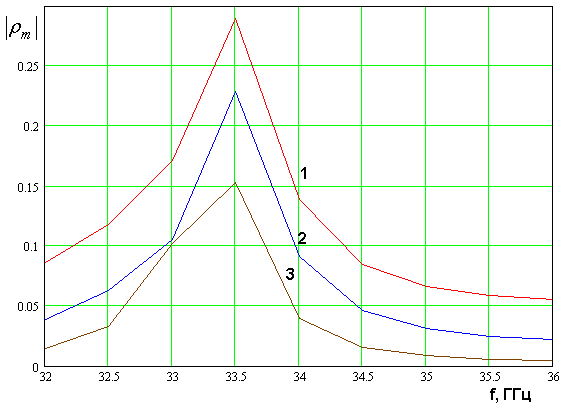
Рис. 13. Частотная зависимость модулей коэффициентов отражения
Резонировать в рупоре
может не только волна с ![]() , как в рассмотренных
выше примерах, но и волны других порядков, когда раскрыв рупора близок к
критическому сечению выделенной волны. Наиболее опасными являются резонансы
волн с четными номерами. Их поле имеет тот же вид симметрии относительно оси
рупора, что и поле основной волны. Поэтому они возникают в активном канале, в
который включен источник возбуждения облучателя. Волны с нечетными номерами в
активном канале появиться не могут (см. рис. 11 а) из-за разной симметрии их
поля относительно основной волны. По этой причине влияние резонанса таких волн
ослаблено.
, как в рассмотренных
выше примерах, но и волны других порядков, когда раскрыв рупора близок к
критическому сечению выделенной волны. Наиболее опасными являются резонансы
волн с четными номерами. Их поле имеет тот же вид симметрии относительно оси
рупора, что и поле основной волны. Поэтому они возникают в активном канале, в
который включен источник возбуждения облучателя. Волны с нечетными номерами в
активном канале появиться не могут (см. рис. 11 а) из-за разной симметрии их
поля относительно основной волны. По этой причине влияние резонанса таких волн
ослаблено.
В целом по результатам проведенных численных исследований можно сделать следующие выводы. Вне резонансной области частот для оценки ширины главного лепестка ДН можно использовать приближенные методы, в том числе, наиболее простой метод физической оптики. Положение резонанса хорошо описывается решением двумерной граничной задачи. Для оценки таких тонких эффектов, как уровень боковых лепестков предпочтительнее использовать численную трехмерную модель.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект № 12-08-12003/12 офи_м).
1. Банков С.Е. Щелевые интегральные схемы миллиметрового диапазона // Радиотехника и электроника. 2006, Т. 51, №9, с. 1066-1086.
2. Bankov S.E., Bugrova T.I., Levchenko I.V. Planar Lens for Millimeter Wave Integrated Antennas // 24-th European Microwave Conf. Proc., 1994, Nice, France, pp. 76-80.
3. M. Ettorre, S. Bruni, G. Gerini, A. Neto, N. Llombart, S. Maci, Sector PCS-EBG Antenna for Low Cost High Directivity Applications, Antennas and Wireless Propagation Letters, Vol.6, pp. 537-539, Dec. 2007.
4. А.с. 1316063 (СССР). Планарный резонатор / Банков С.Е., Взятышев В.Ф., Широкова О.А. Приор. От 18.11.85. Опубл. БИ №21, 7.06.87.
5. Взятышев В.Ф., Нарытник Т.Н., Рябов Б.А., Емельяненков Б.Н., Банков С.Е. Диэлектрические интегральные схемы КВЧ. Часть 2. Элементы и устройства // Обзоры по электронной технике. - М.: ЦНИИ “Электроника”, 1985, Вып. 13, 73 с.
6. Банков С.Е., Весник М.В. Квазиоптический возбудитель антенной решетки на основе EBG структуры // РЭ. 2009. Т. 54. № 11, С. 1256-1266.
7. Сазонов Д.М. Антенны и устройства СВЧ. М.: Высш. Шк. 1998.
8. Корнблит С. СВЧ оптика. М.: «Связь». 1980.
9. Справочник по расчету и конструированию СВЧ полосковых устройств. Под. ред. Вольмана В.И. М.: Радио и связь. 1982.
10. Банков С.Е. Волноводы с нелокальными границами // Журнал радиоэлектроники. № 6. 2008. URL: http://jre.cplire.ru/iso/jun08/5/contents.html.
11. Нефедов Е.И., Фиалковский А.Т. Полосковые линии передачи. М.: Наука. 1980.
12. Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. М.: Радио и связь. 1983.
13. Банков С.Е., Курушин А.А. Расчет излучаемых структур с помощью FEKO. М.: Издательство ЗАО НПП «Родник». 2008.