УДК 004.934.2
МАРКОВСКИЕ МОДЕЛИ В ЗАДАЧАХ ПАРАМЕТРИЗАЦИИ РЕЧЕВЫХ СИГНАЛОВ
Д. Е. Прозоров, К. В. Плетнев
Вятский государственный университет
Вятский государственный гуманитарный университет
Статья получена 2 июня 2014 г.
Аннотация. В статье исследована возможность применения методов параметризации речевых сигналов простыми и сложными (многосвязными) цепями Маркова в системах автоматического распознавания команд (АРК). Показано, что параметризация речевых сигналов многосвязными цепями Маркова позволяет достичь компромисса между эффективностью распознавания речевых команд и вычислительной сложностью алгоритма параметризации. Низкая вычислительная сложность алгоритмов марковской параметризации свидетельствуют о возможности значительного снижения требований к вычислительным ресурсам систем АРК.
Ключевые слова: распознавание речи, параметризация, многосвязная цепь Маркова.
Abstract: The article investigates the possibility of using of the speech parameterization methods by simple and complex (multivariable) Markov chains in systems of automatic recognition of commands (ARC). It is shown that the speech parametrization by multivariable Markov chains allows to reach a compromise between the efficiency of speech recognition commands and computational complexity of the algorithm parameterization. Low computational complexity Markov parameterization indicate the possibility of a significant reduction in requirements for computational complexity of ARC.
Key words: speech recognition, parameterization, multivariate Markov chain.
1. Введение
К настоящему времени разработано большое количество моделей и методов параметризации речевых сигналов, обеспечивающих высокое качество работы систем автоматического распознавания речевых команд (АРК), среди которых наиболее распространены методы, основанные на расчете кепстральных коэффициентов и коэффициентов линейного предсказания речи [1-3].
Однако нельзя сказать, что задача параметризации полностью решена. Производительность систем АРК еще далека от «производительности» человеческой слуховой системы. Например, в задаче распознавания цифр, когда словарь мал и существенная часть ресурсов тратится на акустическое моделирование, производительность систем АРК на порядок ниже производительности человека [4]. Отчасти это связано с большим количеством скрытых и явных переменных состояния современных систем АРК. Таким образом, задача разработки моделей и методов параметризации речевых сигналов, позволяющих найти компромисс между производительностью, требованиям к ресурсам и качеством работы систем АРК остается актуальной.
Первые работы, посвященные марковским моделям речевых сигналов появились еще 1970-х годах. Так, в монографии [5] проведен подробный анализ марковских моделей дельта-модулированных речевых сигналов. Тем не менее, малое количество публикаций, посвященных исследованию методов марковской параметризации речевых сигналов и такие достоинства марковских моделей как относительно небольшое количество параметров и линейная вычислительная сложность алгоритмов расчета параметров, продолжают вызывать интерес к указанным методам.
В данной статье рассмотрены марковские модели в задачах параметризации речевых сигналов.
2. Постановка задачи
Пусть фрагмент речевого сигнала представлен массивом дискретных отсчетов
где 
– k-я
двоичная выборка вида
, 
, 
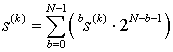, (2)
L – длина фрагмента.
Фрагмент (1) можно рассматривать
как суперпозицию битовых последовательностей 
, (3)
где 
–
операция скалярного умножения, 
– бинарная
последовательность, образованная b-м
битом двоичных выборок фрагмента речевого сигнала.
Ряд экспериментов [5,6] показывает,
что для речевых сигналов справедливо допущение о практически монотонном
уменьшении корреляционных связей между выборками 
и 
речевого сигнала с увеличением интервала 
между выборками. Следовательно, можно
указать интервал 
, за пределами которого
корреляционные связи практически не распространяются. С учетом этого допущения,
для описания и анализа коротких фрагментов речевых сигналов можно использовать
математический аппарат простых или сложных цепей Маркова.
Требуется разработать модель и метод параметризации фрагмента речевого сигнала (1).
3. Многосвязная цепь Маркова
Рассмотрим
многосвязную (связности m) однородную цепь Маркова с 
состояниями и вероятностями перехода вида
, (4)
где 
, .
Перейдем
от многосвязной цепи Маркова к простой, формируя вектор 
длины
m [7].
Тогда
где 
.
Число
состояний полученной таким образом простой цепи Маркова равно 
.
При известных условных вероятностях (4) можно определить вероятности перехода
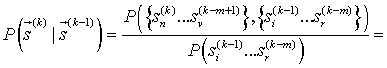
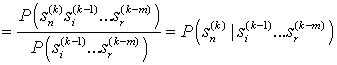, (6)
где .
Например,
при 
и 
переходные
вероятности (6) принимают вид
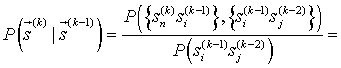
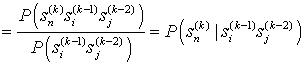, (7)
где 
.
Переходные
вероятности (7) образуют матрицу вида (8) для четырех комбинаций состояний 
, 
, 
, 
:
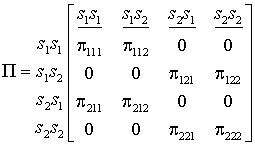, (8)
где 
, .
Нулевые элементы матрицы (8) соответствуют вероятностям невозможным событий.
Подобным
образом можно получить матрицы переходных вероятностей для общего случая (
, 
). Для элементов
матриц вида (8) должны соблюдаться модифицированные условия нормировки
, 
(9)
и согласованности
, 
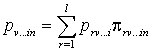, (10)
где 
– безусловная вероятность комбинации из m
состояний
.
В работе [7] показано, что для введенной таким образом простой цепи Маркова соблюдаются разностные уравнения
, (11)
где 
– вектор безусловных вероятностей всех
возможных комбинаций из m
состояний
на -м шаге. Например, для
. (12)
Рассмотрим метод марковской параметризации фрагментов речевых сигналов, использующий описанную модель.
4. Метод параметризации цепью Маркова
Метод параметризации фрагмента речевого сигнала цепью Маркова связности m содержит следующую последовательность шагов.
1.
Битовые последовательности 
(
) объединяются в непересекающиеся массивы 
размера 
.
Обозначим
, 
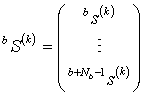. (13)
Будем полагать, что последовательность
(14)
является многосвязной
цепью Маркова связности m с количеством состояний равным 
. Преобразуем многосвязную цепь (14) в
простую цепь Маркова, с количеством состояний равным 
формируя
векторы (5)
(15)
и векторные последовательности
2.
Последовательности 
разделяется на 
пересекающихся сегментов 
с коэффициентом перекрытия h.
3.
Для каждого q-го сегмента последовательности
производится оценка элементов 
матрицы вероятностей переходов 
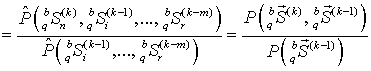, (17)
где , 
, , 
; 
– относительная частота комбинаций 
в q-м
сегменте последовательности 
; 
– относительная частота комбинации
состояний 
в q-м
сегменте последовательности .
Полученные
матрицы вероятностей переходов объединяются в матрицу
параметров сигнала
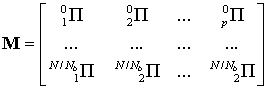. (18)
Поскольку матрица (18) является разреженной, в качестве параметров фрагмента речевого сигнала достаточно использовать только ее значащие элементы.
Пример
1.
,
, 
.
1.
Из фрагмента речевого сигнала выделяются бинарные битовые последовательности , 
(рис.1).
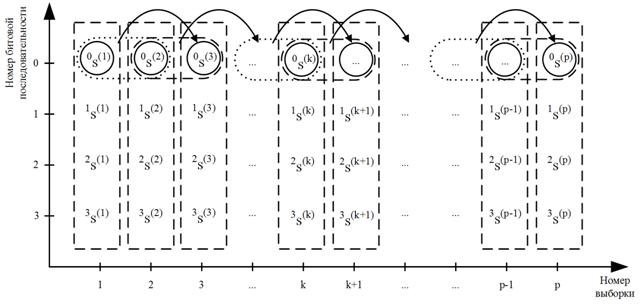
Рис.1. Эпюры
переходов в многосвязной цепи Маркова при и .
Полагая,
что последовательности являются цепями Маркова
связности с количеством состояний равным двум, преобразуем
их в простые цепи Маркова, с количеством состояний равным четырем, формируя
векторы
, (19)
где 
и векторные последовательности (16).
Диаграмма возможных переходов между метасостояниями в таких последовательностях представлена на рис.2.
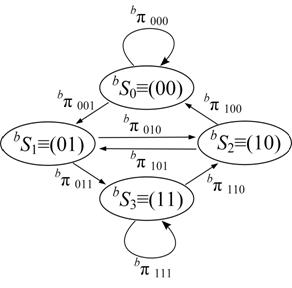
Рис. 2.
Диаграмма переходов в последовательностях при .
2.
Последовательности 
разделяются на p
пересекающихся сегментов с коэффициентом перекрытия h: .
3.
Для каждого q-го сегмента
последовательности производится оценка элементов 
матриц вероятностей переходов
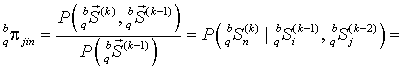
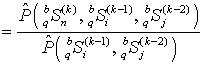, (20)
где 
, , , .
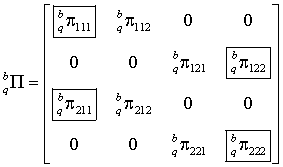. (21)
Нулевые
элементы матрицы (21) соответствуют вероятностям невозможных переходов. Из
примера нетрудно заметить, что невозможны переходы: 
, 
, , 
, 
, 
, 
, 
, 
, где 
, 
, 
, 
.
Поскольку элементы матрицы вероятностей переходов (21) удовлетворяют условию нормировки
, 
, (22)
в качестве параметров
сегмента 
достаточно использовать только значения
элементов 
.
В
результате каждый сегмент характеризуется
матрицей параметров
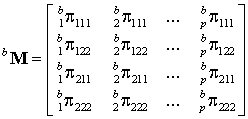. (23)
4. Матрицы bM (23) объединяются в итоговую матрицу параметров фрагмента речевого сигнала
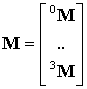. (24)
Пример
2.
,, 
.
1.
Бинарные битовые последовательности 
объединяются в
последовательности 
(рис.3), такие что
,
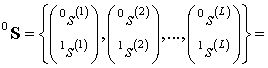
(25)
.
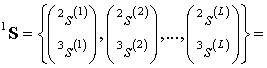
Количество
метасостояний 
таких последовательностей равно
.
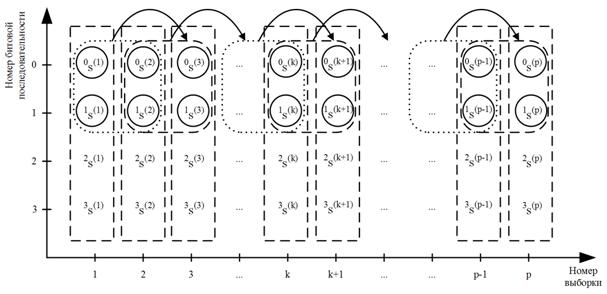
Рис.3. Эпюры
переходов в многосвязной цепи Маркова при и .
Полагая,
что последовательности являются многосвязными цепями
Маркова связности и количеством состояний равным
четырем
, 
, 
, 
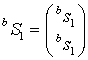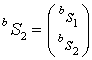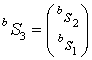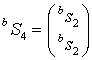, (26)
преобразуем их в
простые цепи Маркова, с количеством состояний равным 
формируя
векторы
(27)
и векторные последовательности
(16).
2.
Последовательности разделяются на p
пересекающихся сегментов с коэффициентом перекрытия h: 
и 
.
3.
Для каждого q-го сегмента
последовательности производится оценка элементов матриц вероятностей переходов
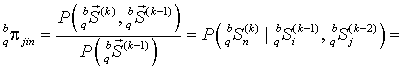
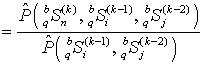, (28)
где 
, , , 
.
4.
Ненулевые элементы матриц вероятностей переходов объединяются в матрицу параметров сигнала
.
5. Эксперимент
Рассмотренные в статье модели речевых сигналов использованы для оценки эффективности методов марковской параметризации при решении задачи дикторозависимого распознавания речевых команд. В качестве альтернативного метода параметризации речевых сигналов применен метод параметризации мел-кепстральными коэффициентами (MFCC).
Для эксперимента сформирована авторская коллекция из 150 речевых команд с частотой дискретизации 8 кГц.
Эксперимент заключался в выполнении следующих шагов:
1) оценке среднего времени параметризации одного фрагмента речевого сигнала;
2) оценке вероятности правильного распознавания команд в результате выполнения 1000 опытов для каждой модели (табл.1).
Результаты
эксперимента представлены в табл.1. Для обозначения модели используемой при
параметризации введены следующие сокращения: общее название модели dtmc
(Discrete Time
Markov Chain),
следующие две цифры обозначают порядок цепи Маркова – и
количество группируемых битовых последовательностей – 
.
В скобках указаны номера старших бит, используемых при параметризации.
Таблица 1 – Вероятность распознавания и время параметризации
|
|
Метод параметризации |
Относительное время параметризации одного фрагмента |
Вероятность распознавания, % |
|
|
Простая цепь |
dtmc11(0) |
37,7 |
0,052 |
76,3 |
|
dtmc11(0,1) |
40,4 |
0,055 |
83,5 |
|
|
dtmc11(0,1,2) |
42,5 |
0,058 |
84,2 |
|
|
dtmc11(0,1,2,3) |
45,0 |
0,062 |
84,7 |
|
|
dtmc12(0,1) |
37,4 |
0,051 |
85,3 |
|
|
dtmc12(0,1,2,3) |
40,3 |
0,055 |
89,7 |
|
|
Сложная цепь |
dtmc21(0) |
37,9 |
0,052 |
83,4 |
|
dtmc21(0,1) |
40,4 |
0,055 |
92,4 |
|
|
dtmc21(0,1,2) |
42,7 |
0,059 |
94,8 |
|
|
dtmc21(0,1,2,3) |
44,9 |
0,062 |
95,8 |
|
|
dtmc22(0,1) |
37,9 |
0,052 |
85,6 |
|
|
dtmc21(0,1,2,3) |
40,4 |
0,055 |
93,9 |
|
|
|
MFCC |
728,1 |
1 |
99,7 |
Эксперимент показал (табл.1), что компромисс между эффективностью распознавания речевых команд и вычислительной сложностью алгоритма параметризации достигается при использовании (для оценки параметров аппроксимирующей цепи Маркова) от одного до четырех старших бит равномерно квантованного речевого сигнала.
Полученные результаты (табл. 1) свидетельствуют о значительном (в 16-19 раз) снижении временных затрат на параметризацию фрагментов речевых сигналов при сопутствующем уменьшении вероятности распознавания команд на 5-8% относительно классического метода параметризации мел-кепстральными коэффициентами.
Выводы
В
работе обобщены варианты представления фрагментов речевых сигналов простыми и
сложными (многосвязными) цепями Маркова. Представлены частные случаи реализации
данных моделей при параметризации речевых сигналов многосвязными цепями Маркова
связностью 
и .
Показано, что при использовании методов марковской параметризации в задачах автоматического дикторозависимого распознавания речевых команд (АРК) целесообразно применение моделей многосвязных цепей Маркова. Рассмотренные модели речевых сигналов позволяют значительно снизить требования к вычислительным ресурсам систем АРК.
Литература
1. Рабинер, Л.Р. Цифровая обработка речевых сигналов / Рабинер Л.Р., Шафер Р.В. // Пер. с англ. Под ред. Прохорова Ю.Н., Назарова М.В. – М.: Радио и связь, 1981. – 496 c.
2. Huang, X. Spoken Language Processing: A guide to theory, algorithm, and system development / X. Huang, A.Acero, H.Hon. // Prentice Hall. – 2001.
3. Zheng. Comparison Of Different Implementations Of MFCC / F. Zheng, G. Zhang, Z. Song // Computer Science & Technology, 16(6): 2001. - pp. 582-589.
4. Picone, J.W. Signal modeling techniques in speech recognition / proceedings of the IEEE, September 1993, pp. 1215-1247.
5. Венедиктов М.Д. Дельта-модуляция. Теория и применение / Венедиктов М.Д., Женевский Ю.П., Марков В.В. - М.: Связь, 1976. C. 104-114.
6. Плетнев К.В. Анализ метода марковской параметризации речевых сигналов / Плетнев К.В., Прозоров Д.Е. // Информационные системы и технологии, 2014. – №1(81). – С. 24-29.
7. Яншин В.В. Многосвязные цепи Маркова и их свойства // Радиотехника и электроника, Наука. 1993. – Том 38. – № 6 – С. 1081-1091.