УДК 621.396

Оценка точностных параметров радиолокационных стендов ДЛЯ измерениЯ характеристик радиолокационных изображений исследуемых объектов

 

С. И. Моряков ¹, С. М. Нестеров¹  , И. А. Скородумов ¹,  С. Н. Приймаков ²

¹ Научно-исследовательской институт Войск ВКО Минобороны России

² Ростовский–на–Дону научно-исследовательский институт радиосвязи

Статья получена 10 июня 2014 г.

 

Аннотация.  В работе предложен способ оценки точностных параметров радиолокационных стендов, осуществляющих построение одномерных и двумерных радиолокационных изображений (РЛИ), измерение эффективной площади рассеяния (ЭПР) и координат локальных центров рассеяния объектов при их зондировании широкополосными сигналами.

Ключевые слова: эффективная площадь рассеяния, инверсное синтезирование апертуры, широкополосные радиолокационные стенды, радиолокационные изображения.

Abstract: The paper proposes a method of estimating the precision parameters radar systems offering to generate one-and two dimensional radar images, measuring the radar cross section and the coordinates of the local centers of scattering objects by sensing their wideband signals.

Key words: radar cross section, wideband radar systems, radar images, inverse synthetic aperture.

 

В настоящее время все большее практическое применение получают широкополосные радиолокационные системы с режимом формирования двумерных изображений объектов [1,2,3]. Для разработки и совершенствования таких систем необходимы данные по ЭПР в широкой полосе частот и радиолокационные изображения (РЛИ) типовых объектов, получаемые на радиолокационных стендах. В этой связи актуальным становится вопрос об аттестации измерительного стенда с целью получения оценок точности измеряемых им параметров по построенным радиолокационным изображениям объектов. Такими параметрами являются, в первую очередь, ЭПР и координаты локальных центров рассеяния объекта. Оценка точности может быть проведена путем сравнения полученных на стенде экспериментальных данных с результатами известного строгого решения дифракционной задачи для сферы.

            Цель работы – обеспечить поверку (аттестацию) радиолокационных стендов, формирующих РЛИ исследуемых объектов.

Рассмотрим двумерное радиолокационное изображение объекта в виде двух эталонных металлических сфер диаметром 70см и 12см (рис.1), скрепленных малоотражающим устройством на расстоянии около 3м друг от друга. Изображение получено на открытом измерительном комплексе известным [4] методом инверсного синтезирования апертуры путем преобразования Фурье комплексных огибающих отраженных от объекта сигналов, измеренных при многочастотном импульсном зондировании и записанных в координатах пространственных частот. В ходе эксперимента объект вращался в горизонтальной плоскости с постоянной скоростью. Зондирование объекта осуществлялось импульсным периодическим сигналом со ступенчатой перестройкой частоты с постоянным шагом. Параметры сигнала: полоса перестройки частоты 4,25…5,75 ГГц (относительная полоса перестройки 30%), 512 импульсов в пачке, длительность импульса 0,3мкс, период следования 10мкс. При построении изображения использовано 8-микратное добавление сигнала нулями и его обработка в весовом окне Хемминга с соответствующей нормировкой амплитуды [5].

Изображение на рис.1 сформировано относительно связанной с объектом декартовой системы координат и представляет собой совокупность откликов от элементов объекта разной мощности в координатах относительной дальности z и поперечной координаты x плоскости локации. Измеренные отраженные сигналы прокалиброваны мерами ЭПР, поэтому мощность откликов на РЛИ выражена в единицах ЭПР. Диапазон значений мощности отражен цветовой палитрой.

 

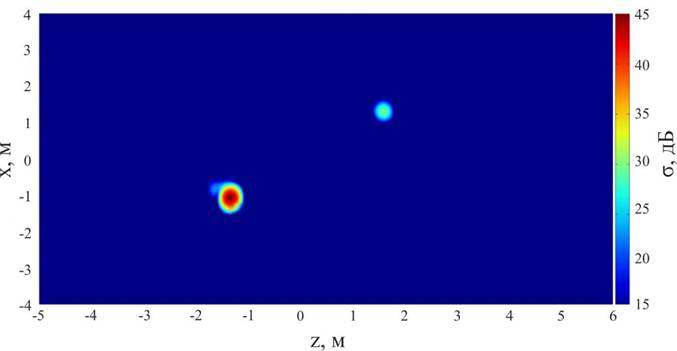
Рис.1. Радиолокационное изображение объекта в виде двух эталонных металлических сфер

На качество получаемых радиолокационных изображений объектов влияют различные погрешности, основные из которых связаны с амплитудно-частотными и фазочастотными характеристиками измерительной аппаратуры и принимаемых отраженных сигналов, алгоритмами их калибровки, ошибками системы координатной привязки объекта и алгоритмами обработки радиолокационной информации. Поэтому важное значение приобретает оценка интегральной погрешности всего процесса формирования РЛИ, которую предлагается получить путем измерения значений местоположения и мощности максимумов откликов от эталонных металлических сфер разного размера и их сравнения с соответствующими расчетными значениями.

Известно [6], что для очень малых сфер фазовый центр рассеяния совпадает с центром сферы, а по мере роста волнового размера сфер сдвигается, осуществляя колебания в резонансной области рассеяния и асимптотически приближаясь в высокочастотной области к положению, отстоящему от передней кромки сферы на четверть длины волны. Расчеты и эксперименты также показывают, что в резонансной области рассеяния ЭПР сферы можно полагать результатом суперпозиции двух локальных центров рассеяния: большей мощности, который формирует передняя кромка сферы, и меньшей – огибающая волна. С увеличением размера сферы мощность отражения передней кромкой увеличивается, относительный уровень мощности центра рассеяния огибающей волны снижается и с учетом имеющегося отношения сигнал/фон может не идентифицироваться на РЛИ.

Применительно к оценке параметров откликов от сфер по их радиолокационным изображениям это означает необходимость учета влияния огибающей волны на мощность и местоположение основного отклика, даже если отклик от огибающей волны на РЛИ не зафиксирован.

 

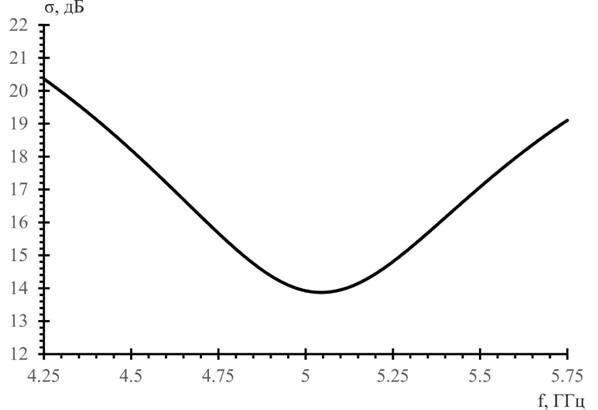
Рис.2. Зависимость ЭПР сферы диаметром 3,3см от частоты

С учетом измерения отраженных сигналов в широкой полосе частот возникает также вопрос о том, каким частотам, мощности и местоположению должен соответствовать максимум основного отклика от сферы, по которому естественно проводить оценку точности измерений. Этот вопрос иллюстрирует рис.2, на котором приведена зависимость от частоты ЭПР сферы диаметром 3,3см.

Из рис.2 видно, что значения ЭПР в указанной выше полосе частот меняются от 13,9дБ до 20,2дБ. Значение ЭПР сферы на средней частоте равно 13,93дБ. Среднее значение ЭПР сферы в этой полосе частот – 16,57дБ.

Для иллюстрации появления на радиолокационных изображениях сферы локального центра рассеяния огибающей волны и его уровня рассчитаны и приведены на рис.3 и рис.4 соответственно отклики от сфер диаметром 3,3см и 20см в виде зависимости ЭПР s в относительных единицах от относительной дальности z. Изображения получены с использованием 16-кратного добавления сигнала нулями и весовой обработки в окне Хемминга.

 

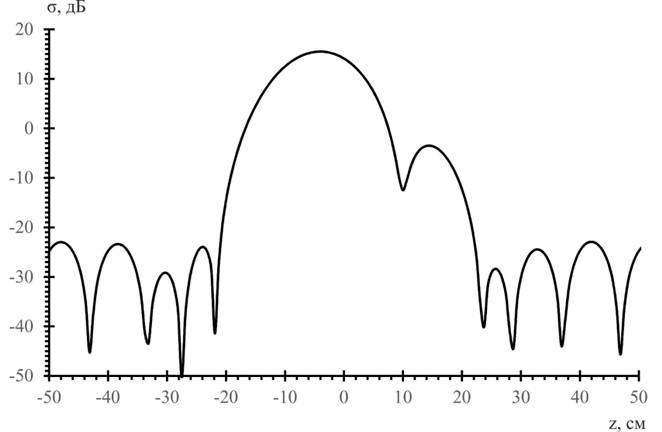
Рис.3. Отклик (профиль дальности) от сферы диаметром 3,3см

 

Рис.4. Отклик (профиль дальности) от сферы диаметром 20см

Не ограничивая общности рассуждений, рассмотрим далее задачу формирования одномерного РЛИ объекта по дальности (профиль дальности) без весовой обработки (в прямоугольном окне).

Дискретная форма оператора синтезирования одномерного РЛИ за счет перестройки частоты имеет вид

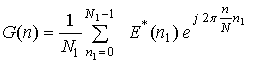,                                                       (1)

 

где  - комплексная амплитуда отраженного от объекта сигнала, приведенная к центру синтезирования (к единой дальности);

 - амплитуда отклика;

=0, …, -1 - номер частоты;

 - количество частот;

=0, …, -1 - номер дискреты дальности;

 - количество дискрет дальности,.

Используя свойство линейности преобразования Фурье, оценим значение амплитуды максимального отклика, сдвинув начало системы координат в положение максимума. Получаем

.

 

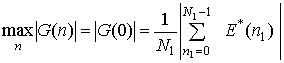Если объект формирует один доминирующий отклик, то оценка мощности его максимума в единицах ЭПР без учета изменения фазы равна

,                                                                                         (2)

где 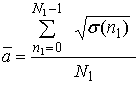      - среднее значение амплитуды отраженного сигнала;

 

 - ЭПР объекта на частоте номер .

Определим погрешность оценки (2).

Используя известный размер дискреты дальности (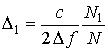, где  - полоса перестройки частоты;  - скорость света), перепишем (1) относительно

координаты дальности

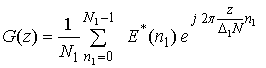                                                     (3)

 

и решим задачу поиска местоположения максимума гладкой функции (3) численным методом.

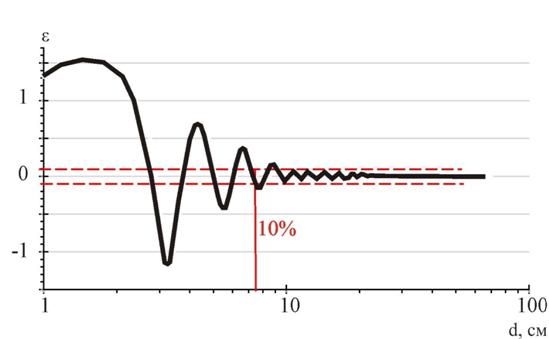
На рис.5 приведены результаты численных расчетов в виде зависимости  от диаметра сферы d, которая дает меру отличия местоположения по дальности максимума основного отклика  от координаты передней кромки сферы .

Рис.5. Отличия местоположения по дальности максимума основного отклика от координаты передней кромки сферы

Полученная зависимость показывает, что основной отклик от сферы c увеличением ее размера удаляется от центра сферы до 0,5 радиуса в сторону задней кромки (при диаметре 1см), с дальнейшим увеличением диаметра сферы меняет направление перемещения и приближается к передней кромке (при диаметре 2,9см), затем выходит из сферы, приближаясь еще более чем на радиус (при диаметре 3,3см), затем снова начинает удаляться, касается передней кромки (при диаметре 3,8см), углубляется внутрь на расстояние немногим более 0,5 радиуса (при диаметре 4,5см) и, претерпевая дальнейшие колебания вперед-назад относительно передней кромки с уменьшающейся амплитудой, асимптотически к ней приближается. Начиная со сфер диаметром 7,5см, отклонения координаты максимума отклика от передней кромки не превышают 10%.

Зависимость мощности максимума основного отклика от диаметра сферы приведена на рис.6 (кривая 2). Эта зависимость сопоставлена с зависимостью ЭПР сферы от ее диаметра на средней частоте рассматриваемой полосы (кривая 1).

 

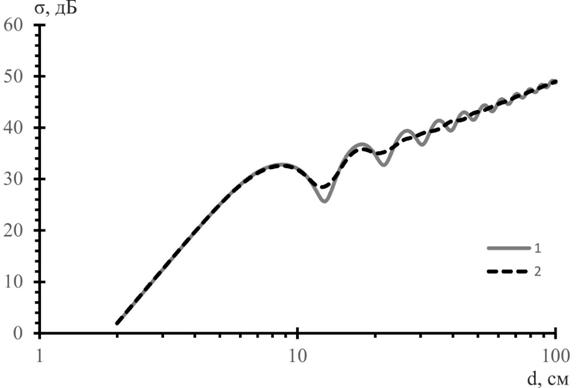
Рис.6. Зависимость мощности максимума основного отклика от диаметра сферы

 

                     

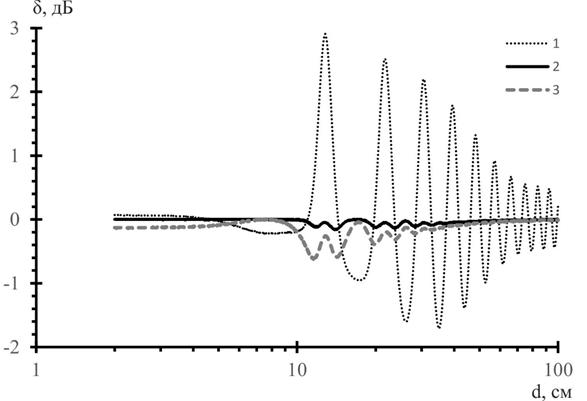
Рис.7. Абсолютная погрешность оценки мощности максимума основного отклика от сферы

На рис.7 приведены зависимости абсолютной погрешности d оценок мощности максимума основного отклика значениями ЭПР сферы на средней частоте (кривая 1), средней ЭПР сферы в полосе частот (кривая 3) и квадрата средней амплитуды отраженного сферой сигнала (кривая 2).

Полученные результаты подтверждают вывод о том, что наименьшую погрешность имеет оценка ЭПР отклика по квадрату средней амплитуды отраженного сферой сигнала в полосе перестройки частоты зондирования. Эта погрешность не превышает -0,15дБ для сфер резонансного размера и практически равна нулю в релеевской и высокочастотной областях. Оценка по средней ЭПР имеет погрешность до -0,6дБ, а по ЭПР на средней частоте – от -1,7дБ до 2,8дБ.

Показано, что погрешность измерений значений ЭПР локальных центров рассеяния объекта на уровнях от   10^-5 м² до 1 м² может быть установлена путем сравнения значения измеренного максимума основного отклика от металлической сферы соответствующего размера с квадратом средней амплитуды отраженного сферой сигнала в рассматриваемой полосе частот. Погрешность оценки координат локальных центров рассеяния объекта может быть оценена по положению максимума основного отклика от эталонной сферы, который должен соответствовать дальности до передней кромки для сфер большого волнового размера (с уровнями ЭПР от нескольких тысячных м² и выше), а для сфер с уровнями ЭПР 10^-3 м² и меньше – расчетной зависимости, приведенной на рис.5.

Предложенный способ оценки точности измерения значений эффективной площади рассеяния и координат локальных центров рассеяния объектов при их зондировании широкополосными сигналами может быть положен в основу методики аттестации широкополосных радиолокационных измерительных стендов.

 

Литература

1.     Ковалев С.В., Нестеров С.М., Скородумов И.А. Двумерные радиолокационные изображения эталонных объектов // Радиотехника и Электроника. 2011. Т.56. №2.

2.     Cumming, I.G., Wong F.H Digital Processing of Synthetic Aperture Radar Data. - Norwood, MA.: Artech House, 2005.

3.     Ozdemir Caner. Inverse synthetic aperture radar imaging with MATLAB. – Hoboken, NJ.: John Wiley & Sons, 2012.

4.     Методы исследования радиолокационных характеристик объектов. Монография / Под ред. С.В. Ягольникова. – М.: Радиотехника, 2012.

5.       L.R. Burges, R.P. Flam, C.N. Nadovich. Calibration and Normalization of Windowed RCS Images. – Horsham, Pa.: Flamm and Russel inc, 1990.

6.     Кобак В.О. Радиолокационные отражатели. – М.: Сов.радио, 1975.