|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 3, 2002 |
|
МЕТОД ИДЕНТИФИКАЦИИ ОБЪЕКТА УПРАВЛЕНИЯ НА ВХОДЕ И ВЫХОДЕ КОТОРОГО СЛУЧАЙНЫЕ ПРОЦЕССЫ С ПЕРЕМЕННЫМ ВО ВРЕМЕНИ СРЕДНИМ ЗНАЧЕНИЕМ
Кузнецов С.Н.
Северо-Кавказский государственный технологический университет
Получена 3 марта 2002 г.
В работе разработан метод идентификации объекта на входе и выходе которого случайные процессы с переменным во времени средним значением. Получено выражение для передаточной функции объекта, учитывающее как стационарные случайные процессы, так и тренды. Для этого выведены аналоги по Лапласу спектральных плотностей случайных процессов. Показано применение разработанного метода на тестовом примере и практическом примере коммутатора Gigabit Ethernet.
1. ВВЕДЕНИЕ
2. АНАЛОГ ПО ЛАПЛАСУ ДВОЙНОЙ ПО ЧАСТОТЕ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ СЛУЧАЙНЫХ ПРОЦЕССОВ
3. ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ И ПЕРЕХОДНОЙ ХАРАКТЕРИСТИКИ ОБЪЕКТА
4. ПРИМЕРЫ
5. ЗАКЛЮЧЕНИЕ
6. ЛИТЕРАТУРА
Важной частью проектирования систем автоматического управления является идентификация объектов управления. Под идентификацией понимается определение оператора связывающего входные и выходные переменные.
Практически любая система автоматического управления работает под действием случайных возмущений и помех. Это и определяет использование методов теории случайных процессов для анализа и синтеза систем управления.
Задача идентификации не представляет трудности если временные ряды на входе и выходе объекта управления являются реализациями стационарных случайных процессов, но в большинстве реальных объектов процессы нестационарные.
Еще Норбертом Винером [1] был разработан спектральный метод идентификации для линейных объектов, когда на его вход и выход действуют эргодические стационарные случайные процессы. Значительный вклад в развитие теории случайных процессов и спектральных методов был сделан А.Я.Хинчиным, А.Н.Колмогоровым, В.А.Котельниковым, В.С.Пугачевым [2], [3], [4], [5]. Эти методы были доведены до инженерного применения Дж.Бендатом [6-10]. Кроме того, появились и инженерные методы параметрической идентификации, основанные на авторегрессии - скользящем среднем [11], [12]. Недостатком этих методов является то, что при наличии тренда (оценки математического ожидания переменной во времени) он просто удаляется (detrending). Но зависимости между трендами на входе и выходе и зависимости между случайными процессами на входе и выходе могут быть различными, поэтому тренды нужно не удалять, а учитывать их влияние.
Классические спектральные методы используют преобразование Фурье, применение
которого весьма ограничено из-за условий накладываемых на преобразуемую функцию
[13]. Для существования интеграла
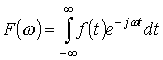 ,
где
,
где
![]() достаточно,
чтобы выполнялись условия:
достаточно,
чтобы выполнялись условия:
1) Абсолютной интегрируемости
![]() ,
то есть
,
то есть
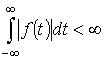 .
.
2) Функция
![]() должна
быть кусочно-непрерывной и иметь ограниченное изменение на каждом конечном
отрезке оси
должна
быть кусочно-непрерывной и иметь ограниченное изменение на каждом конечном
отрезке оси
![]() .
.
Тренды же могут быть и показательными и степенными и другими функциями, для которых не существует преобразования Фурье.
Поэтому, вместо преобразования Фурье, для учета влияния тренда следует
использовать преобразование Лапласа [13]. Для существования
преобразования Лапласа
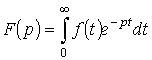 ,
достаточно, чтобы выполнялись условия:
,
достаточно, чтобы выполнялись условия:
1) Функция
![]() должна
удовлетворять условиям Гельдера всюду на оси
должна
удовлетворять условиям Гельдера всюду на оси
![]() ,
кроме отдельных точек, где она имеет разрывы первого рода, причем на каждом
конечном интервале таких точек конечное число. Это означает, что для каждого
,
кроме отдельных точек, где она имеет разрывы первого рода, причем на каждом
конечном интервале таких точек конечное число. Это означает, что для каждого
![]() (кроме
указанных исключительных точек) существуют положительные постоянные
(кроме
указанных исключительных точек) существуют положительные постоянные
![]() ,
,
![]() ,
,
![]() такие,
что
такие,
что
![]() для
всех
для
всех
![]() ,
,
![]() .
.
2) Функция
![]() для
всех отрицательных
для
всех отрицательных
![]() .
.
3) Функция
![]() возрастает
не быстрее показательной функции, то есть существуют такие постоянные
возрастает
не быстрее показательной функции, то есть существуют такие постоянные
![]() ,
,
![]() ,
что для всех
,
что для всех
![]() -
-
![]() .
.
Эти условия выполняются для большинства физических процессов.
Обозначим через
![]() -
случайный процесс с переменным во времени средним значением на входе объекта,
-
случайный процесс с переменным во времени средним значением на входе объекта,
![]() -
тренд (математическое ожидание) на входе объекта,
-
тренд (математическое ожидание) на входе объекта,
![]() -
стационарный случайный процесс на входе объекта,
-
стационарный случайный процесс на входе объекта,
![]() -
случайный процесс с переменным во времени средним значением на выходе объекта,
-
случайный процесс с переменным во времени средним значением на выходе объекта,
![]() -
тренд (математическое ожидание) на выходе объекта,
-
тренд (математическое ожидание) на выходе объекта,
![]() -
стационарный случайный процесс на выходе объекта.
-
стационарный случайный процесс на выходе объекта.
Предположим, что для
![]() и
и
![]() существуют
изображения по Лапласу
существуют
изображения по Лапласу
![]() и
и
![]() ,
где
,
где
![]() и
и
![]() -
изображения трендов (математических ожиданий)
-
изображения трендов (математических ожиданий)
![]() и
и
![]() ,
,
![]() и
и
![]() -
изображения стационарных случайных процессов,
-
изображения стационарных случайных процессов,
![]() -
изображение возмущающего воздействия.
-
изображение возмущающего воздействия.
Рис. 1.
Для идентификации объекта следует вывести выражение для передаточной функции
объекта
![]() ,
которая учитывала бы как влияние тренда, так и случайной составляющей (рис.
1).
,
которая учитывала бы как влияние тренда, так и случайной составляющей (рис.
1).
Математическую модель объекта в этом случае можно представить, как
![]() .
.
Для того, чтобы получить передаточную функцию
![]() ,
следует в начале вывести выражения для аналогов по Лапласу двойных по частоте
спектральных плотностей случайных процессов.
,
следует в начале вывести выражения для аналогов по Лапласу двойных по частоте
спектральных плотностей случайных процессов.
2. АНАЛОГ ПО ЛАПЛАСУ ДВОЙНОЙ ПО ЧАСТОТЕ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Двойная по частоте взаимоспектральная плотность между случайными процессами на
входе и выходе, определяется как математическое ожидание от
комплексно-сопряженного преобразованного по Фурье случайного процесса на входе
![]() умноженного
на преобразованный по Фурье случайный процесс на выходе
умноженного
на преобразованный по Фурье случайный процесс на выходе
![]() [5]:
[5]:
![]() ,
,
где "*" обозначает сопряженную комплексную величину.
Подобные представления существует и для автоспектральных плотностей случайных
процессов
![]() и
и
![]() [5]:
[5]:
![]() ,
,
![]() .
.
Причем в преобразованиях Фурье используются разные частоты
![]() и
и
![]() .
Аналогично в преобразовании Лапласа будем использовать отличные друг от друга
комплексные переменные
.
Аналогично в преобразовании Лапласа будем использовать отличные друг от друга
комплексные переменные
![]() и
и
![]() .
.
Пусть заданы случайные процессы с переменным во времени средним значением
![]() и
и
![]() ,
изображения которых
,
изображения которых
![]() и
и
![]() .
.
Определим аналоги по Лапласу взаимоспектральных и автоспектральных плотностей случайных процессов.
Аналог по Лапласу взаимной спектральной плотности случайных процессов
![]() и
и
![]() представим,
как математическое ожидание произведения их изображений
представим,
как математическое ожидание произведения их изображений
![]() .
.
Подобным образом, аналог по Лапласу автоспектральной плотности случайного
процесса
![]() можно
определить как
можно
определить как
![]() .
.
Для случайного процесса
![]() аналог
по Лапласу автоспектральной плотности имеет вид:
аналог
по Лапласу автоспектральной плотности имеет вид:
![]() .
.
Тогда для аналога взаимоспектральной плотности будем иметь
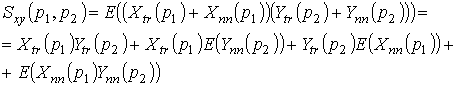 .
.
Поскольку
![]() и
и
![]() -
величины неслучайные, то
-
величины неслучайные, то
Таким же образом можно получить выражения и для аналогов автоспектральных плотностей:
Преобразуем выражение (1) исходя из того, что
взаимокорреляционная функция есть математическое ожидание от произведения
![]() на
на
![]() [5],
то есть
[5],
то есть
![]() .
.
Следовательно,
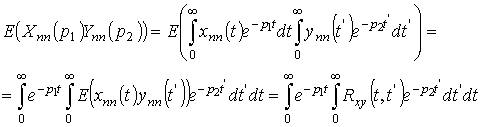 .
.
Но для стационарных случайных процессов корреляционные функции зависят
только от разности
![]() ,
то есть
,
то есть
![]() [5],
тогда
[5],
тогда
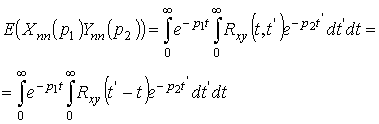 .
.
Пусть
![]() ;
;
![]() ,
тогда преобразуя предыдущее выражение получим,
,
тогда преобразуя предыдущее выражение получим,
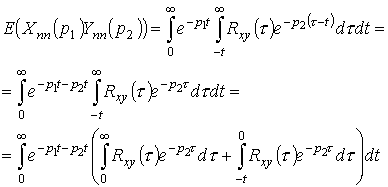 .
.
Из свойств взаимокорреляционных функций известно, что
![]() [5],
следовательно,
[5],
следовательно,
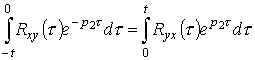 ,
тогда
,
тогда
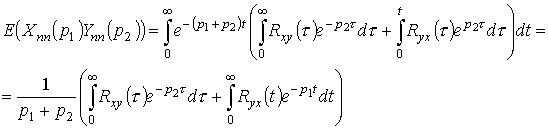 .
.
Последнее соотношение получено с учетом того, что
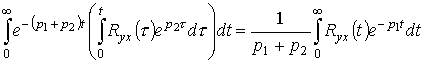 .
.
Обозначая через
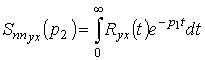 и
и
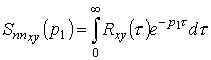 ,
получим окончательное соотношение для математического ожидания произведения
стационарных случайных процессов (аналог взаимоспектральной плотности)
,
получим окончательное соотношение для математического ожидания произведения
стационарных случайных процессов (аналог взаимоспектральной плотности)
![]() и
и
![]()
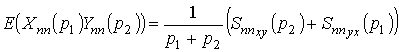 .
.
Окончательно, для случайных процессов
![]() и
и
![]() имеем
выражение взаимоспектральной плотности по Лапласу
имеем
выражение взаимоспектральной плотности по Лапласу
Подобным образом из выражений (2) и (3)
можно вывести соотношения для аналогов по Лапласу автоспектральных плотностей
случайных процессов
![]() и
и
![]() :
:
где
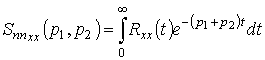 и
и
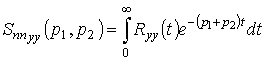 .
.
Причем при выводе нужно учесть, что автокорреляционная функция стационарного
случайного процесса - функция четная, то есть
![]() [5].
[5].
Следует отметить, что односторонние спектральные плотности являются частным
случаем аналогов по Лапласу спектральных плотностей случайных процессов, когда
![]() и
и
![]() .
.
После вывода выражений для аналогов по Лапласу спектральных плотностей следует перейти к определению передаточной функции, связывающей вход и выход объекта.
3. ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ И ПЕРЕХОДНОЙ ХАРАКТЕРИСТИКИ ОБЪЕКТА
Постановка задачи. Пусть на входе и выходе объекта случайные
процессы с переменным средним значением
![]() и
и
![]() ,
для которых существует преобразование Лапласа. Требуется определить передаточную
функцию
,
для которых существует преобразование Лапласа. Требуется определить передаточную
функцию
![]() ,
связывающею вход и выход объекта. То есть
,
связывающею вход и выход объекта. То есть
Решение задачи.
Минимизируем математическое ожидание квадрата модуля ошибки между
![]() и
и
![]() :
:
![]() .
.
Следуя Дж.Бендату [6] ошибку
![]() представим
как возмущающее воздействие на выходе объекта (рис. 1). Для этого умножим
представим
как возмущающее воздействие на выходе объекта (рис. 1). Для этого умножим
![]() на
сопряженную комплексную величину
на
сопряженную комплексную величину
![]() и
возьмем от произведения математическое ожидание
и
возьмем от произведения математическое ожидание
Соотношение (8) получено исходя из того, что
![]() -
функция детерминированная.
-
функция детерминированная.
Так как в преобразовании Лапласа пределы интегрирования действительные величины,
и под знаком интеграла только
![]() является
комплексной величиной, а остальные величины - действительные, то
является
комплексной величиной, а остальные величины - действительные, то
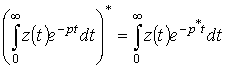 ,
,
тогда
![]() .
.
Аналогично и для выражений:
![]() ,
,
![]() .
.
Следовательно, для случая когда
![]() аналоги
спектральных плотностей (4), (5), (6),
примут вид (индексы "1" и "2" можно опустить):
аналоги
спектральных плотностей (4), (5), (6),
примут вид (индексы "1" и "2" можно опустить):
где
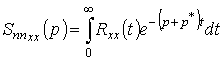 и
и
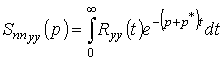 .
.
Или в сокращенной форме записи соотношение (8), примет вид
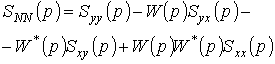 ,
,
где
![]() .
.
Мнимая часть аналогов автоспектральных плотностей равна нулю:
![]() ,
,
![]() ,
,
![]() ,
,
а действительная часть положительна, так как в правой части выражений:
![]() ,
,
![]() ,
,
![]() ,
,
произведения величин комплексных на комплексно-сопряженные.
Тогда выражение (8) будет имеет вид
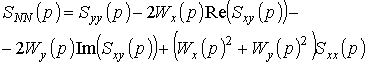 ,
,
где
![]() ,
,
![]() .
.
Необходимым условием существования экстремума функции является равенство нулю первых производных функции:
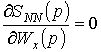 ,
,
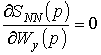 .
.
Продифференцируем
![]() по
по
![]() и
и
![]() ,
получим:
,
получим:
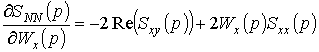 ,
,
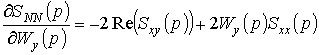 .
.
Прировняв к нулю полученные выше соотношения, будем иметь:
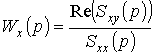 ,
,
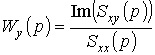 .
.
Следовательно, выражение для передаточной функции объекта имеет вид:
или в развернутой форме
Теперь докажем, что выполняется и достаточное условие существование минимума
функции
![]() .
Для этого возьмем вторые производные от этой функции:
.
Для этого возьмем вторые производные от этой функции:
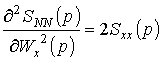 ,
,
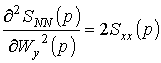 .
.
Достаточное условие выполняется, так как вторые производные и квадратичная форма
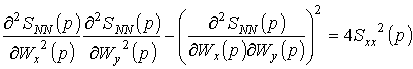
величины положительные, в следствии того, что
![]() положительная
действительная величина.
положительная
действительная величина.
Для получения импульсной переходной характеристика объекта
![]() используется
обратное преобразование Лапласа
используется
обратное преобразование Лапласа
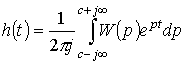 .
.
В случае, если
![]() и
и
![]() ,
а также для случая когда
,
а также для случая когда
![]() ,
,
![]() и
и
![]() ,
функция
,
функция
![]() не
является комплексной аналитической функцией относительно переменной
не
является комплексной аналитической функцией относительно переменной
![]() в
полуплоскости
в
полуплоскости
![]() .
Передаточная функция
.
Передаточная функция
![]() -
функция неаналитическая, так как в выражении (13)
присутствуют произведение и сумма комплексно-сопряженных величин. Однако
передаточная функция
-
функция неаналитическая, так как в выражении (13)
присутствуют произведение и сумма комплексно-сопряженных величин. Однако
передаточная функция
![]() есть
комплексная аналитическая функция относительно
есть
комплексная аналитическая функция относительно
![]() ,
за исключением некоторых особых точек.
,
за исключением некоторых особых точек.
Поэтому формулу обращения Лапласа преобразуем так, чтобы переменной
интегрирования была
![]() .
Интегрирование в обратном преобразовании производится по прямой
.
Интегрирование в обратном преобразовании производится по прямой
![]() ,
следовательно, полагая
,
следовательно, полагая
![]() и
и
![]() ,
получим формулу обращения Лапласа в виде [13]
,
получим формулу обращения Лапласа в виде [13]
Из выражений (13) и (14) видно, что
импульсная переходная характеристика
![]() будет
зависеть от
будет
зависеть от
![]() .
Изменяя величину
.
Изменяя величину
![]() можно
изменить вклад вносимый в передаточную функцию
можно
изменить вклад вносимый в передаточную функцию
![]() трендами
и стационарными случайными процессами. Например, при
трендами
и стационарными случайными процессами. Например, при
![]() выражение
(10) имеет вид
выражение
(10) имеет вид
то есть в этом случае передаточная функция учитывает только стационарные случайные процессы.
Теперь получим выражение для частотной передаточной функции. Поскольку, кроме
частных случаев,
![]() не
является комплексной аналитической функцией, то получить частотную передаточною
функцию заменой
не
является комплексной аналитической функцией, то получить частотную передаточною
функцию заменой
![]() на
на
![]() в
выражении (13) нельзя. В результате такой замены будем иметь
соотношение (15), которое учитывает только стационарные
случайные процессы.
в
выражении (13) нельзя. В результате такой замены будем иметь
соотношение (15), которое учитывает только стационарные
случайные процессы.
Поэтому сначала рассмотрим интеграл
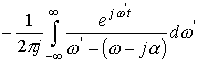 .
.
Этот интеграл берется по контуру, ограничивающему нижнюю полуплоскость. Знак минус перед интегралом присутствует потому, что обход контура берется против часовой стрелки.
Так как функция
![]() является
функцией аналитической в нижней полуплоскости и непрерывнa
на действительной оси, то согласно формуле Коши [13]
является
функцией аналитической в нижней полуплоскости и непрерывнa
на действительной оси, то согласно формуле Коши [13]
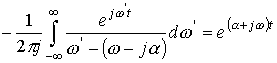 .
.
Возьмем от предыдущего выражения преобразование Фурье
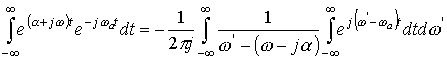 .
.
Подставляя в это соотношение аналитическое выражение для дельта-функции [5]
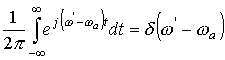 ,
,
и учитывая, что дельта-функция является функцией четной [5]
![]() ,
,
получим
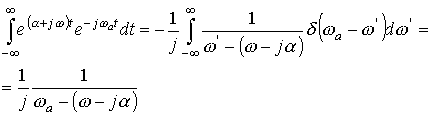 .
.
Следовательно, преобразование Фурье от функции
![]() имеет
вид
имеет
вид
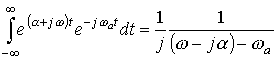 .
.
Интеграл в последнем выражении понимается в смысле главного значения по Коши.
Теперь возьмем от импульсной переходной характеристики (14) преобразование Фурье
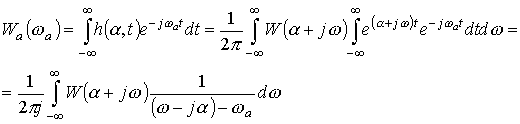 .
.
Таким образом, выражение для определения частотной передаточной функции по передаточной функции имеет вид:
После определения передаточной функции можно моделировать процессы на выходе
объекта по входу объекта. Процесс на выходе объекта
![]() можно
представить в виде свертки
можно
представить в виде свертки
![]() и
и
![]() :
:
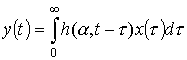 .
.
Стоит отметить, что для численных расчетов передаточной функции можно воспользоваться либо коррелограммным, либо периодограммными методами [6], [12], используя вместо финитного преобразования Фурье финитное преобразование Лапласа.
3.1. Тестовый пример
Пусть на входе объекта (рис. 2) процесс состоящий из
гауссова случайного процесса с математическим ожиданием равным
![]() ,
и среднеквадратическим отклонением
,
и среднеквадратическим отклонением
![]() ,
то есть
,
то есть
![]() и
тренда в виде функции Хевисайда
и
тренда в виде функции Хевисайда
![]()
![]() .
.
На выходе объекта (рис. 3) процесс состоящий из гауссова
случайного процесса с математическим ожиданием равным
![]() ,
и среднеквадратическим отклонением
,
и среднеквадратическим отклонением
![]() ,
то есть
,
то есть
![]() и
тренда в виде функции
и
тренда в виде функции
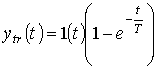 с
постоянной времени
с
постоянной времени
![]()
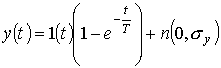 .
.
Рис.2.
Рис. 3.
Изображения по Лапласу трендов
![]() и
и
![]() имеют
вид:
имеют
вид:
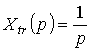 ,
,
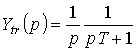 .
.
Автокорреляционную функцию гауссова случайного процесса на входе объекта, можно представить, как
![]() ,
,
где
![]() -
дельта-функция Дирака.
-
дельта-функция Дирака.
Взаимокорреляционные функции случайных процессов будут иметь следующий вид:
![]() ,
,
![]() .
.
Тогда беря преобразование Лапласа от корреляционных функций получим аналоги по Лапласу автоспектральной и взаимоспектральной плотностей гауссовых случайных процессов:
![]() ,
,
![]() ,
,
![]() .
.
Следовательно, выражения (9) и (10) для аналогов по Лапласу автоспектральной и взаимоспектральной плотностей процессов на входе и выходе объекта, примут вид:
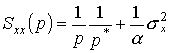 ,
,
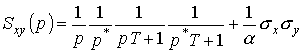 .
.
Для данного случая передаточная функция объекта (12) имеет следующий вид
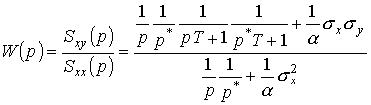 .
.
Модуль частотной передаточной функций (16) при
![]() представлен
на рис. 4, фазочастотная характеристика объекта - на рис. 5.
представлен
на рис. 4, фазочастотная характеристика объекта - на рис. 5.
Рис. 4.
Рис. 5.
Передаточная функция трендов является передаточной функцией апериодического звена
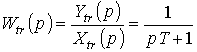 ,
,
а передаточная функция гауссовых случайных процессов
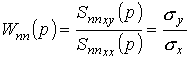
- передаточной функцией пропорционального звена (рис. 4). Передаточная функция объекта на частотах ниже 0.15 Гц совпадает с передаточной функцией трендов, а на частотах выше 11 Гц совпадает с передаточной функцией стационарных случайных процессов. Таким образом передаточная функция меняется от передаточной функции трендов к передаточной функции стационарных случайных процессов.
На рис. 6 показаны результат моделирования процесса на выходе объекта и исходный процесс на выходе объекта.
Рис. 6.
3.2. Практический пример (коммутатор Gigabit Ethernet)
Для проектирования высокопроизводительных коммутаторов Gigabit Ethernet представляет практический интерес зависимость поведения очереди во входном буфере порта коммутатора от межкадрового интервала входящего потока кадров. В этом случае, на входе объекта подлежащего идентификации межкадровый интервал, а на выходе - длина очереди. Входные и выходные процессы являются случайными процессами с нестационарным средним. На рис. 7 представлен график входного процесса, при среднем уровне загрузки канала 0.78. На рис. 8 представлен график выходного процесса при среднем уровне загрузки коммутационного устройства 0.5. При идентификации использовались те же данные, что и в работе [14]. Тренды выделялись методами линейного регрессионного анализа.
Рис. 7.
Рис. 8.
Передаточная функция была получена периодограммным методом Барлетта оценки спектральной плотности [12], в котором дискретное преобразование Фурье заменено дискретным преобразованием Лапласа.
Модуль частотной передаточной функций при
![]() представлен
на рис. 9, фазочастотная характеристика объекта - на
рис. 10.
представлен
на рис. 9, фазочастотная характеристика объекта - на
рис. 10.
Рис. 9.
Рис. 10.
На рабочих частотах отсчетов, передаточная функция объекта является передаточной функцией интегрирующего звена (рис. 9). Данный вывод совпадает с физикой процессов протекающих в коммутационном устройстве и подтверждает выводы сделанные в работе [14].
Рис. 11.
На рис. 11 показаны результат моделирования процесса на выходе объекта и исходный процесс на выходе объекта.
В работе поставлена и решена задача разработки метода идентификации объекта на входе и выходе которого случайные процессы с переменным во времени средним значением.
Метод позволяет учитывать при идентификации как тренды на входе и выходе так и стационарные случайные процессы на входе и выходе объекта. Вместо преобразования Фурье применено преобразование Лапласа. Поэтому получены аналоги по Лапласу двойных по частоте спектральных плотностей случайных процессов.
Минимизируя математическое ожидание квадрата модуля ошибки, выведено выражение для передаточной функции объекта.
В работе показано применение разработанного метода на тестовом примере, а также практическом примере коммутатора Gigabit Ethernet.