|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 3, 2004 |
|
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ДИФРАКЦИИ В ВОЛНОВОДЕ МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ
А.Н. Боголюбов, А.Л. Делицын, А.В. Лаврёнова
Московский государственный университет им. М. В. Ломоносова,
физический факультет, кафедра математики
Получено 31 марта 2004 г.
В работе рассматривается задача рассеяния нормальной моды на неоднородности в волноводе. Для ее решения применяется метод конечных элементов. Построен и реализован алгоритм численного расчета данной задачи методом конечных элементов, при этом для ограничения области используются парциальные условия излучения, а в качестве базисных функций берутся как билинейные на элементах, так и биквадратные базисные функции. Проведено сравнение результатов применения билинейных и биквадратных конечных элементов.
Содержание
ВАРИАЦИОННАЯ ПОСТАНОВКА ЗАДАЧИ
АЛГОРИТМ ПОСТРОЕНИЯ РЕШЕНИЯ ЗАДАЧИ
ВВЕДЕНИЕ
В настоящее время большой интерес представляет разработка эффективных численных алгоритмов для расчета нерегулярных волноведущих систем, в частности, систем с локальными неоднородностями. Поскольку такие системы имеют, как правило, сложную геометрию и неоднородное заполнение, то встает вопрос об использовании наиболее универсальных численных алгоритмов для их исследования. Такие алгоритмы могут быть построены на основе метода конечных разностей в прямой и вариационной постановках (проекционно-сеточные методы, например, метод конечных элементов [1, 2]). Отметим, что, хотя метод конечных разностей для расчета электродинамических систем стал применяться относительно недавно, в настоящее время он достаточно широко используется для решения как прямых, так и обратных задач электродинамики [3, 4]. Обладая большими преимуществами, метод конечных разностей вызывает и определенные сложности при своем использовании. Одной из таких сложностей является проблема ограничения области, в которой ищется решение. В случае, если неоднородность в волноводе носит локальный характер, для ограничения области удобно использовать разностные аналоги парциальных условий излучения, впервые предложенных А.Г. Свешниковым в работе [5]. Впервые такой подход был использован А.Н. Боголюбовым и А.Г. Свешниковым в работе [6], посвященной расчету плоского волновода методом конечных разностей. Однако при расчете волноведущих систем проекционно-сеточными методами, в частности, методом конечных элементов, ограничение области с помощью разностных аналогов парциальных условий излучения до настоящего времени применялось недостаточно широко.
МЕТОД РЕШЕНИЯ ЗАДАЧИ
Метод конечных элементов завоевал всеобщее признание как весьма эффективный метод решения самых разнообразных задач математической физики и техники [7-9]. Высокая популярность этого метода объясняется простотой его физической интерпретации, а также ясностью и четкостью численного алгоритма, что существенно облегчает программирование сложных задач математической физики. В своей основе этот метод является вариационным. Его возникновение и развитие связано с классическими работами Галеркина, Бубнова и Ритца.
Метод конечных элементов основан на локальной аппроксимации решения кусочно-полиномиальными функциями. Исходная область разбивается на подобласти стандартного вида, в качестве которых выступают треугольники или четырехугольники. Делая подобласть достаточно малой, либо выбирая достаточно высокую степень полиномов, можно добиться того, чтобы аппроксимирующая функция достаточно точно передавала локальное поведение решения. Этот метод может применяться для областей произвольной формы и граничных условий общего вида, причем возможно нерегулярное разбиение области. Таким образом, на расположение элементов при разбиении области не накладываются ограничения, что позволяет применять метод конечных элементов для широкого круга областей без использования глобальной фиксированной системы координат.
Применение метода конечных элементов к решению задач математической физики и, в частности, к расчету волноведущих систем имеет два аспекта. С одной стороны, это построение эффективных алгоритмов для решения конкретных задач из достаточно широких классов. С другой стороны, это исследование вопроса о повышении точности численного метода при сохранении экономичности. Одним из основных методов улучшения точности является повышение степени аппроксимирующих решение функций, берущихся в качестве базисных, в методе конечных элементов. В настоящей работе демонстрируется быстрый рост точности метода при замене линейных конечных элементов квадратичными.
ПОСТАНОВКА ЗАДАЧИ
Запишем математическую
постановку задачи дифракции электромагнитных волн на локальной неоднородности в
волноводе без поглощения (двумерный случай). Стенки волновода предполагаются
идеально проводящими. Пусть ось ![]() направлена по оси волновода, а ось
направлена по оси волновода, а ось ![]() – перпендикулярно оси
– перпендикулярно оси ![]() . В связи с решением
задачи дифракции на неоднородности в волноводе рассматривается задача для
уравнения Гельмгольца:
. В связи с решением
задачи дифракции на неоднородности в волноводе рассматривается задача для
уравнения Гельмгольца:
![]() (1)
(1)
в
области ![]() с
однородными граничными условиями на боковой поверхности волновода:
с
однородными граничными условиями на боковой поверхности волновода:
![]() (2)
(2)
![]() (3)
(3)
где
![]() – поле в
волноводе,
– поле в
волноводе, ![]() –
диэлектрическая проницаемость:
–
диэлектрическая проницаемость:
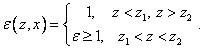
(4)
k – волновое число.
Вне области D (z1 < z < z2), где заключена неоднородность заполнения, поле можно представить в виде разложения по системе собственных волн:
![]() ,
,
где
![]() ,
, ![]() ,
, ![]() – собственные значения и
собственные функции индуцированной задачи в сечении.
– собственные значения и
собственные функции индуцированной задачи в сечении.
В
данном случае сечением является отрезок ![]() , поэтому
, поэтому
![]()
![]()
![]()
Так
как для распространяющейся волны с вещественным ![]() , задача может рассматриваться только для
, задача может рассматриваться только для ![]() ниже частоты отсечки – в
данном случае
ниже частоты отсечки – в
данном случае ![]() .
.
На сечениях волновода плоскостями z=z1 и z=z2 поставим парциальные условия излучения, которые позволяют рассматривать внутреннюю краевую задачу с нелокальными краевыми условиями:
![]()
(5)
![]()
(6)
где
![]() – скалярное
произведение:
– скалярное
произведение: ![]() а
а
![]() – падающая
волна, для которой и рассматривается дифракция.
– падающая
волна, для которой и рассматривается дифракция.
ПАРЦИАЛЬНЫЕ УСЛОВИЯ ИЗЛУЧЕНИЯ
В нашей задаче уравнения (5) и (6) – парциальные условия излучения. Покажем, как ставятся эти граничные условия.
В полых полубесконечных частях волновода представим поле разложением по собственным волнам:
![]()
(7)
где
![]()
![]()
(8)
учитывая отсутствие волн, приходящих из бесконечности, кроме падающей волны.
Нам надо получить стандартные граничные условия вида:
![]() .
.
Для этого продифференцируем разложения (7) и (8).
При
![]()
![]()
(9)
Коэффициенты
![]() можно
заменить коэффициентами Фурье для поля в разложении по собственным функциям
сечения
можно
заменить коэффициентами Фурье для поля в разложении по собственным функциям
сечения ![]() :
:
![]()
откуда
![]() (10)
(10)
Подставляя (10) в (9), получаем
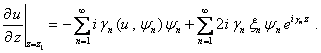
Соответственно
на сечении ![]() :
:

Аналогично
для ![]()
![]()
![]() .
.
Итак,
для сечения ![]()
![]() .
.
ВАРИАЦИОННАЯ ПОСТАНОВКА ЗАДАЧИ
Классическое решение задачи (1)-(6) должно быть дважды
дифференцируемо. Для поиска решения в пространстве ![]() воспользуемся слабой (вариационной)
постановкой:
воспользуемся слабой (вариационной)
постановкой:
![]()
которая для дважды дифференцируемых функций эквивалентна ранее поставленной задаче.
Для вывода вариационной постановки умножим уравнение Гельмгольца
![]()
скалярно
на функцию ![]() из
того же класса что и
из
того же класса что и ![]() ,
то есть
,
то есть ![]()
![]() .
.
![]() .
.
Применим
к ![]() формулу
Грина
формулу
Грина
![]()
В нашем случае
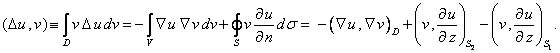
(11)
Интегралы
по части границы ![]() и
и
![]() обращаются в
0, т.к. на этих границах
обращаются в
0, т.к. на этих границах ![]() .
.
Система
собственных волн полна в классе ![]() (
(![]() с однородными граничными условиями при
с однородными граничными условиями при ![]() ,
, ![]() ).
).
Значит,
функцию ![]() тоже
можно разложить в ряд по
тоже
можно разложить в ряд по ![]() :
:
![]()
Подставляем
в (11) это разложение, а производные ![]()
![]() на
на ![]() и
и ![]() заменяем граничными условиями (5), (6).
заменяем граничными условиями (5), (6).
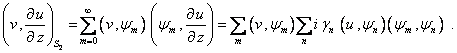
Собственные
функции сечения ![]() ортогональны
друг другу:
ортогональны
друг другу:
![]()
![]()
поэтому
из двух сумм остаются только члены, где ![]() .
.

Аналогично

Подставляя в (11), получаем
![]()
![]()
![]()
Окончательно для уравнения Гельмгольца получаем вариационную постановку в виде:
![]()
Итак, обобщенная постановка задачи, соответствующая краевой задаче (1)-(6), заключается в поиске решения уравнения:
![]() (12)
(12)
что эквивалентно ранее поставленной задаче.
АЛГОРИТМ ПОСТРОЕНИЯ РЕШЕНИЯ ЗАДАЧИ
Для решения задачи (1)-(6) – задачи дифракции электромагнитных волн на локальной неоднородности в волноводе без поглощения применяется метод конечных элементов.
В качестве базисных функций выбираются билинейные и
биквадратные на элементах функции вида: ![]() ,
, ![]() ,
, ![]() . Причем, для билинейных функций
. Причем, для билинейных функций
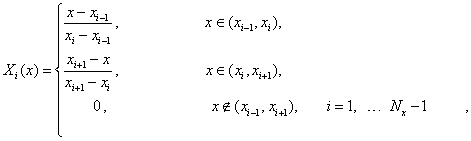
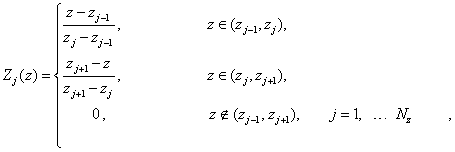
а для биквадратных:
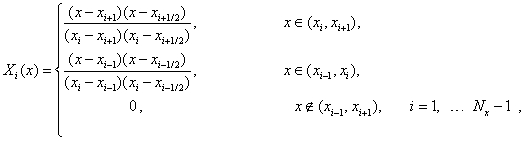
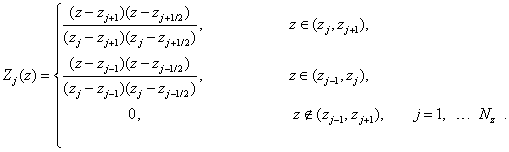
В данном случае сетка равномерная по обеим координатам
![]()
![]()
![]()
![]() .
.
Для
удобства функции ![]() перенумерованы
одним индексом:
перенумерованы
одним индексом:
![]()
![]()
![]()
![]()
![]() .
.
Функцию
![]() в
вариационной постановке приближаем линейной комбинацией базисных функций
в
вариационной постановке приближаем линейной комбинацией базисных функций
![]() ,
, ![]() . (13)
. (13)
Подставив (13) в (12), получаем
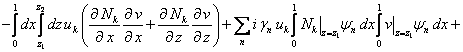

![]()
Здесь
суммы по ![]() –
бесконечные.
–
бесконечные.
Для
наших приближенных вычислений мы обрываем их, заменяя суммой до конечного числа
![]() Функция
Функция ![]() не конкретизируется.
не конкретизируется.
Все
базисные функции ![]() удовлетворяют
однородному граничному условию при
удовлетворяют
однородному граничному условию при ![]() ,
, ![]() .
.
Выбирая
последовательно разные базисные функции ![]() для
для ![]() , для каждой из них получим
, для каждой из них получим
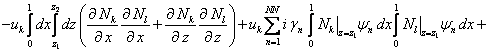

![]()
![]()
Можно
заметить, что ![]() во
все выражения в левой части входят линейно, а в правой части индекс
во
все выражения в левой части входят линейно, а в правой части индекс ![]() не участвует вообще.
Представляя
не участвует вообще.
Представляя ![]() ,
как
,
как ![]() - мерный
столбец, получаем линейное матричное уравнение
- мерный
столбец, получаем линейное матричное уравнение
![]() ,
,
где
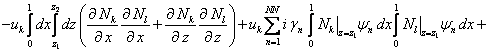 – элементы
матрицы
– элементы
матрицы ![]() ,
размерности
,
размерности ![]() ,
так называемой матрицы жесткости:
,
так называемой матрицы жесткости:


а
правая часть – ![]() -
мерный столбец:
-
мерный столбец:
![]()
Надо
заметить, что матрица ![]() симметрична,
более того, многие элементы в ней равны нулю. Действительно, в выражение для
симметрична,
более того, многие элементы в ней равны нулю. Действительно, в выражение для 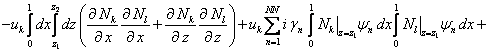 входят произведения
входят произведения ![]() и их производных.
Базисные функции равны нулю в большой части области
и их производных.
Базисные функции равны нулю в большой части области ![]() , поэтому пересечение их не равно
нулю лишь для некоторых сочетаний
, поэтому пересечение их не равно
нулю лишь для некоторых сочетаний ![]() и
и ![]() . Интегралы же по сечениям, где
. Интегралы же по сечениям, где ![]() и
и ![]() встречаются по отдельности,
равны нулю для всех функций, кроме первых
встречаются по отдельности,
равны нулю для всех функций, кроме первых ![]() и последних
и последних ![]() . Это обстоятельство, а также
симметричность матрицы, сильно упрощают как процесс построения матрицы, так и
решение получившейся системы линейных алгебраических уравнений
. Это обстоятельство, а также
симметричность матрицы, сильно упрощают как процесс построения матрицы, так и
решение получившейся системы линейных алгебраических уравнений
![]() .
.
Построение
матрицы ![]() и
столбца правых частей
и
столбца правых частей ![]() заключается
в интегрировании базисных функций и их производных в соответствующих
сочетаниях.
заключается
в интегрировании базисных функций и их производных в соответствующих
сочетаниях.
Отметим, что основная сложность при построении матрицы жесткости заключается в том, что базисные функции не являются непрерывными. Приходится задавать каждую из них, как множество функций на участках сетки, для каждого участка отдельно проводить вычисления, а результат суммировать.
Учет парциальных условий излучения тем более усложняет построение матрицы, что для получения каждого ее элемента нужно для каждой собственной волны отдельно брать интегралы по границам области и затем их суммировать.
В качестве падающей волны в работе берется собственная волна. В результате, любую возможную волну можно разложить в ряд по собственным волнам и результат представить как суперпозицию полей, рассчитанных для нормальных волн.
РЕЗУЛЬТАТЫ
Результаты
решения задачи дифракции электромагнитных волн на локальной неоднородности в
волноводе без поглощения методом конечных элементов представлены для нескольких
видов неоднородности. В качестве падающей волны берется первая собственная
волна, т.е. ![]() ,
которая распространяется вдоль оси
,
которая распространяется вдоль оси ![]() в положительном направлении (ось абсцисс –
ось
в положительном направлении (ось абсцисс –
ось ![]() , ось
ординат – ось
, ось
ординат – ось ![]() ).
).
В дальнейшем на рисунках а) будут представлены конечные элементы первого порядка – базисные функции в методе конечных элементов – билинейные, а на рисунках б) – конечные элементы второго порядка, т.е. базисные функции в методе конечных элементов – биквадратные, и проведено сравнение точности получившегося с помощью двух различных порядков конечных элементов искомого решения.
В качестве пробной задачи для проверки правильности работы алгоритма был исследован полый волновод – без неоднородности (рис.1) (используется билинейная и биквадратная аппроксимации (рис. 1 а), б)) соответственно):
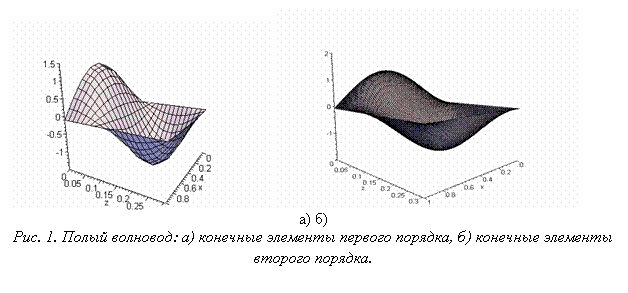
Видно, что волна прошла по волноводу, не исказившись. Поглощение отсутствует.
Более интересными представляются случаи, когда внутри волновода присутствует вставка.
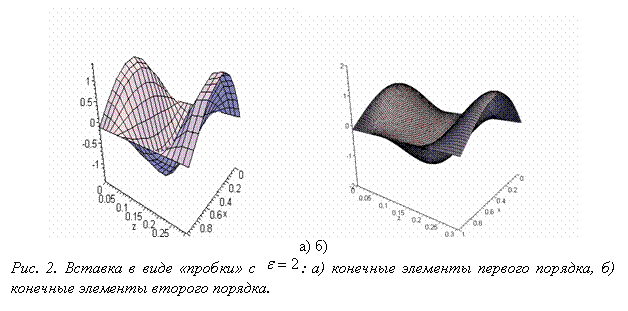
На
рис.2 представлен волновод, если неоднородность имеет вид «пробки», т.е. при ![]() ,
, ![]() . Диэлектрическая проницаемость
. Диэлектрическая проницаемость ![]() . Изменилась длина волны
при прохождении вставки. В отсутствие поглощения амплитуда практически не
изменяется. Четко видно влияние поглощения на изменение амплитуды
распространяющейся по волноводу волны на рис. 3 (в данном случае
. Изменилась длина волны
при прохождении вставки. В отсутствие поглощения амплитуда практически не
изменяется. Четко видно влияние поглощения на изменение амплитуды
распространяющейся по волноводу волны на рис. 3 (в данном случае ![]() ):
):
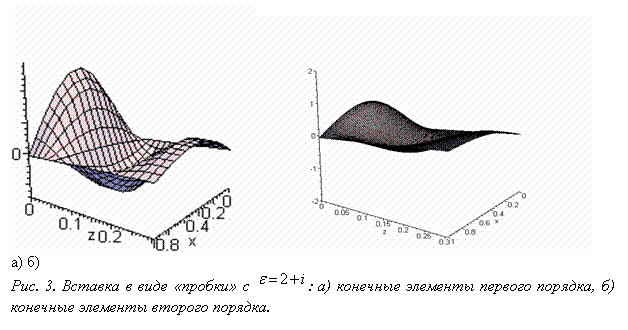
Введение
сильного поглощения: ![]() приводит
к значительному ослаблению интенсивности поля (здесь
приводит
к значительному ослаблению интенсивности поля (здесь ![]() – мнимая часть диэлектрической
проницаемость, а
– мнимая часть диэлектрической
проницаемость, а ![]() –
ее вещественная часть).
–
ее вещественная часть).
При
равенстве ![]() ,
мнимой и вещественной части функции
,
мнимой и вещественной части функции ![]() поле практически полностью гасится
вставкой.
поле практически полностью гасится
вставкой.
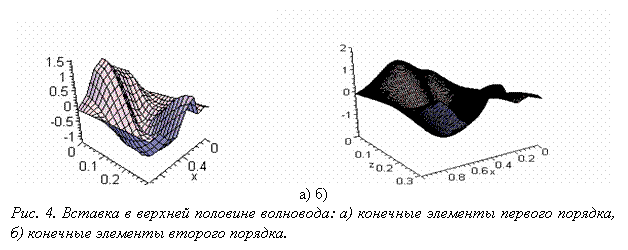
На рис. 4 показана картина распределения поля в
волноводе в случае расположения неоднородности в верхней половине волновода – ![]() ,
, ![]() , а
, а ![]() . При наличии такой несимметрично
расположенной вставки появляется эффект втягивания поля в область с большей
оптической плотностью. Поглощение в данном случае является причиной относительного
выравнивания амплитуды поля в области неоднородности.
. При наличии такой несимметрично
расположенной вставки появляется эффект втягивания поля в область с большей
оптической плотностью. Поглощение в данном случае является причиной относительного
выравнивания амплитуды поля в области неоднородности.
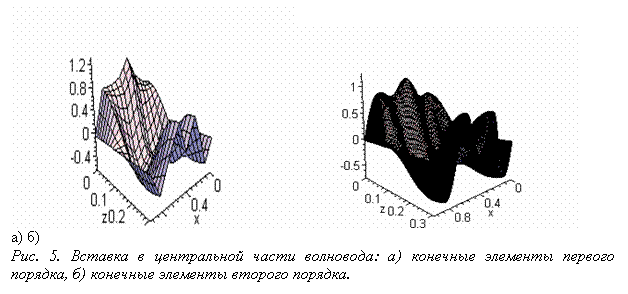
На
рис. 5 показана картина распределения поля в волноводе в случае расположения
неоднородности по середине волновода, ![]() . Четко видно, что при прохождении волны по
волноводу поле концентрируется в центральной области.
. Четко видно, что при прохождении волны по
волноводу поле концентрируется в центральной области.

На
рис. 6 поле распределяется по волноводу, в котором две вставки: ![]() и
и ![]() . Интенсивность поля тем больше,
чем больше значение действительной части
. Интенсивность поля тем больше,
чем больше значение действительной части ![]() .
.
ЗАКЛЮЧЕНИЕ
Проведенные расчеты рассеяния волн на различных видах неоднородностей в плоском волноводе показывают, что метод конечных элементов в комбинации с разностными аналогами парциальных условий излучения позволяет строить достаточно экономичные алгоритмы решения данной задачи. Из сравнения рис. 1-6 а) с рис. 1-6 б) соответственно можно заключить, что повышение степени аппроксимации приводит к значительно более точному вычислению распространяющегося поля уже на грубой сетке.
ЛИТЕРАТУРА
- Марчук Г.И., Агошков В.И. Введение в проекционно-сеточные методы. Москва. Наука. 1981.
- Самарский А.А. Теория разностных схем. Москва. Наука. 1983.
- Боголюбов А.Н., Делицын А.Л., Красильникова А.В., Минаев Д.В., Свешников А.Г. Математическое моделирование волноведущих систем на основе метода конечных разностей // Зарубежная радиоэлектроника. Успехи современной радиоэлектроники. 1998. № 5. С.39-54.
- Боголюбов А.Н., Красильникова А.В., Минаев Д.В., Свешников А.Г. Метод конечных разностей для решения задач синтеза волноведущих систем // Математическое моделирование. 2000. Т.12. № 1. С.13-24.
- Свешников А.Г. Принцип излучения // ДАН СССР. 1950. Т. 3. № 5. С. 517-520.
- Свешников А.Г., Боголюбов А.Н. Применение итерационного метода к исследованию волноводов с неоднородным заполнением // ЖВМиМФ. 1974. T.14. № 4. С. 947-954.
- Свешников А.Г., Боголюбов А.Н. Применение итерационного метода к расчету плоского волновода с неоднородным заполнением. Москва. изд-во МГУ. "Вычислительные методы и программирование". 1975. выпуск 24. С. 262-279.
- Свешников А.Г., Боголюбов А.Н. Расчет плоского волноводного трансформатора конечно-разностным методом. Москва. изд-во МГУ. 1978. выпуск 28. С. 118-133.
- Зенкевич О.К. Метод конечных элементов в технике. Москва. Мир. 1975.
 |
 |