Отражение электромагнитной волны от периодической СТРУКТУРЫ, содержащей ферромагнитные слои
Л. Н. Бутько, В. Д. Бучельников, И. В. Бычков, В. Г. Шавров
Челябинский государственный университет
Институт
радиотехники и электроники РАН, 125009 Москва, Россия
Получена 19 марта 2007 г.
Проведено теоретическое исследование влияния межслоевого обменного взаимодействия ферромагнитных (ФМ) слоев через электроны проводимости проводящих прослоек на условия равновесия, отражательную способность и интегральную восприимчивость слоистой структуры ФМ – немагнитный проводник – ФМ. Получены и проанализированы частотные и полевые зависимости коэффициента отражения (КО) электромагнитных волн (ЭМВ) и интегральной восприимчивости при различном числе слоев в структуре для случаев взаимодействующих и не взаимодействующих между собой ФМ слоев. Показано, что различными значениями межслоевого обменного взаимодействия и толщины слоев можно управлять резонансным поведением КО от структуры. Вблизи ориентационного фазового перехода (ОФП) на низких частотах, а также в области магнитных резонансов в слоях рассматриваемые структуры из полностью отражающих становятся полностью не отражающими. Увеличение числа слоев при учете межслоевого взаимодействия приводит к росту количества и ширины резонансных частотных областей, в которых ЭМВ полностью поглощаются.
1. Введение
Исследование отражательной способности различных веществ является актуальным в связи с потребностью в отражающих и поглощающих электромагнитное излучение материалах. Эти материалы широко применяются в измерительной и контрольной технике, технике связи, радиолокации, медицине и других областях науки и техники. Обычно задачу об уменьшении КО ЭМВ стараются решить путем выравнивания волновых сопротивлений внутри и вне среды или, в частности, при падении волны из вакуума, путем выравнивания величин диэлектрической и магнитной проницаемостей материала. При этом требуется изменять состав вещества, что является довольно сложной проблемой. В настоящее время существуют различные подходы к управлению КО конструкционным путем [1,2]. Однако имеется и другая, более простая возможность управления КО ЭМВ - за счет изменения динамической магнитной проницаемости магнитоупорядоченных веществ и простых изменений структуры в виде различного чередования взаимодействующих магнитных и немагнитных слоев.
В работах [3,4] при учете взаимодействия трех подсистем ферромагнетика (ФМ) (спиновой, упругой и электромагнитной) была теоретически доказана возможность изменения КО ЭМВ от поверхности ФМ от единицы (полное отражение волн) до нуля (полное поглощение волн) при изменении внешних параметров (например, магнитного поля или температуры). В этих работах также была показана принципиальная возможность управления с помощью внешнего магнитного поля КО ЭМВ от поверхности ФМ в широком интервале частот вплоть до гигагерцовых. С физической точки зрения аномальное изменение КО ЭМВ обусловлено эффектом аномального увеличения динамической магнитной проницаемости в области ФМ, магнитоакустического или магнитостатического резонансов, а также при уменьшении частоты спиновых волн за счет уменьшения суммарной магнитной анизотропии в области ОФП [3]. В результате, в области резонансов и вблизи ОФП поведение динамической магнитной восприимчивости становится аномальным, что, в свою очередь, приводит к аномальному уменьшению скорости ЭМВ и аномально большой или аномально малой отражающей способности ФМ.
В работах [3,4] был рассмотрен случай отражения ЭМВ от полубесконечного ФМ. Однако на практике и в эксперименте используются не полубесконечные, а образцы конечной толщины. В последнее время интенсивно исследуются многослойные системы из ФМ слоев, разделенных проводящей прослойкой с толщиной меньше скин-слоя. Структуры, образованные чередованием слоев металла и магнетика, являются новым классом слоистых сред с уникальными электронными и магнитными свойствами, зависящими как от типа материалов, входящих в сверхструктуры, так и от их толщин. Поэтому представляет интерес исследовать, как эти свойства влияют на магнитную проницаемость и отражательную способность таких структур. Современные технологии изготовления слоистых структур (такие, как молекулярно-лучевая эпитаксия) позволяют наносить слои атомной толщины и тем самым управлять её свойствами. Следует также отметить, что полный анализ свойств таких структур невозможен и без решения вопроса о механизме взаимодействия ФМ слоев через проводящие прослойки. Таким механизмом, обеспечивающим сильнодействующую связь между локализованными спинами, находящимися на границах соседних магнитных слоев, может служить косвенный обмен Руддермана-Киттеля-Касуйи-Иосиды (РККИ) [6,7] через электроны проводимости проводящих прослоек.
Все это приводит к целому ряду интересных с практической точки зрения новых физических явлений в рассматриваемых системах.
В данной работе теоретически изучены КО ЭМВ и интегральная магнитная восприимчивость слоистой структуры, состоящей из взаимодействующих между собой диэлектрических ФМ слоев с антипараллельным направлением намагниченностей в них, разделенных немагнитными проводящими (НМП) прослойками.
2. Случай двух ФМ слоев
Рассмотрим сначала структуру, состоящую из двух ФМ слоев (N=2) и одного НМП слоя между ними, находящуюся во внешнем магнитном поле. В этом случае можно аналитически получить дисперсионные уравнения для ФМ слоев. Величина обменной связи между локализованными поверхностными спинами магнитных слоев за счет переноса электронов проводимости проводника сильно зависит от толщины проводящей прослойки [6,7], поэтому, чтобы ее влияние было значимым, толщину прослойки необходимо выбирать порядка 10
[8]. Резонансные особенности на частотных зависимостях КО ЭМВ проявляются особенно отчетливо в случае, когда рассматриваемая структура находится на полубесконечной немагнитной проводящей среде (рис. 1). Предположим, что ФМ слои эквивалентны друг другу и отличаются лишь направлением намагниченности. Абсолютная величина
намагниченности
ФМ слоя является постоянной и направлена в одном слое по оси
, а в другом - в противоположном направлении. Ось
системы координат направим вдоль нормали
к плоскостям раздела сред. Постоянное магнитное поле
||
. Толщины ФМ слоев равны l, а толщина НМП прослоек lm. Будем рассматривать нормальное падение плоской линейно поляризованной ЭМВ
на поверхность структуры.
Рис. 1. Схема слоистой структуры: FM-ферромагнитный слой, NMC-немагнитный проводящий слой, NMe-полубесконечная немагнитная металлическая среда.
Исследование КО ЭМВ проведем методом, основанным на решении связанной системы уравнений Максвелла и Ландау - Лифшица совместно с граничными условиями на векторы напряженности и индукции электромагнитного поля и на намагниченность [3-5]. Совместное этих уравнений с использованием выражения для свободной энергии F слоистой структуры в расчете на единицу площади и граничных условий позволяет получить полную связанную систему линеаризованных уравнений для определения спектра связанных колебаний в ФМ слоях, скорости распространения возбуждений, выражения для интегральной магнитной восприимчивости и для КО ЭМВ.
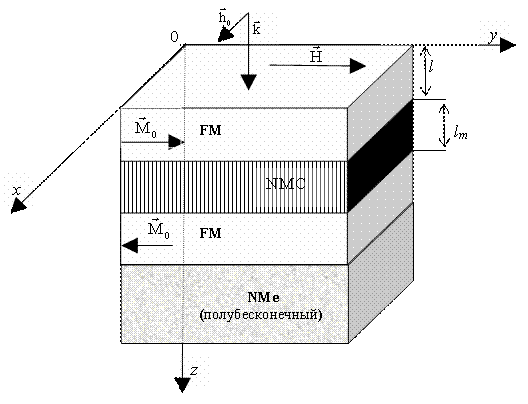
Магнитную часть энергии трехслойной структуры (N=2) в расчете на единицу площади можно записать следующим образом [8]
где
- плотность магнитной энергии n – го (в этом разделе индекс n=1,2) ФМ слоя,
–энергия межслойного взаимодействия. В качестве магнетика выберем ФМ кубической симметрии. В этом случае плотность магнитной энергии для n-го ФМ слоя будет иметь вид [3-5]
где
- множитель Лагранжа, соответствующий условию
,
- постоянная неоднородного обмена, K1 - первая константа кубической анизотропии,
- внешнее магнитное поле. Энергию взаимодействия между ФМ слоями учтем в рамках модели биквадратичного межслойного обмена [8]
здесь J1 и J2 – константы билинейного и биквадратичного обмена,
и
– намагниченности ФМ слоев (рассматривается случай |
| = |
| = M0).
Равновесное направление намагниченности в ФМ слоях находится из условия минимума энергии (1)-(3) – равенства нулю первых производных и не отрицательности матрицы вторых производных свободной энергии. Для рассматриваемой коллинеарной антиферромагнитной (АФМ) структуры получаются следующие условия ее существования
где
,
,
. Здесь и далее верхние знаки соответствуют первому ФМ слою (нечетным слоям в дальнейших разделах), нижние – второму (четным слоям в дальнейших разделах). Знак равенства в неравенстве (4) отвечает точке ОФП первого рода
из коллинеарного АФМ состояния в неколлинеарную АФМ фазу.
При отсутствии внешнего магнитного поля и анизотропии условие устойчивости для АФМ структуры имеет вид:
. Далее будет рассматриваться именно такое соотношение между константами билинейного и биквадратичного обмена.
Из (4) видно, что межслойное взаимодействие приводит к увеличению области существования рассматриваемой АФМ структуры во внешнем магнитном поле. Таким образом, можно заключить, что АФМ слоистая структура при учете межслойного взаимодействия становится более устойчивой во внешнем поле.
Для получения законов дисперсии связанных волн в ФМ слоях воспользуемся системой уравнений Максвелла и Ландау - Лифшица.
,
,
,
;
,
,
где
– эффективное магнитное поле,
- напряженности магнитного и электрического полей соответственно,
- индукция магнитного поля,
- индукция электрического поля,
- статическая диэлектрическая проницаемость,
- скорость света в вакууме,
- гиромагнитное отношение. После линеаризации этой системы уравнений с помощью метода малых колебаний (
, a << A0), получим
,
(5)
где
. Здесь, в этом разделе, индекс n=1,2 соответствует 1-му и 2-му ФМ слоям,
,
,
. Из линеаризованной системы уравнений (5) можно получить дисперсионное уравнение волн, распространяющихся в магнитных слоях. Оно имеет вид
где
,
,
- закон дисперсии невзаимодействующих ЭМВ в ФМ слоях.
Из дисперсионного уравнения (6) следует, что одна из частот связанных колебаний при k=0 обращается в нуль в точке ОФП
. Из анализа дисперсионного уравнения также следует, что две из четырех связанных ветвей колебаний в рассматриваемой структуре являются безактивационными, а остальные – активационными. При k®0 закон дисперсии одной из безактивационных ветвей в точке ОФП (то есть при H=H0) имеет линейный характер, а другой – квадратичный
где
. Отметим, что по аналогии со связанными магнитоупругими волнами [9], данные ветви носят квазиэлектромагнитный характер. Таким образом, из (7) следует, что в точке ОФП скорость одной из ветвей квазиэлектромагнитных колебаний существенно уменьшается, а второй - стремится к нулю при k®0. Активации остальных двух ветвей связанных колебаний в точке ОФП имеют вид
где
. Формула (8) имеет место и вне точки ОФП. В этом случае
.
Решением дисперсионного уравнения (6) относительно волнового числа являются двенадцать значений, соответствующих шести связанным волнам, которые могут распространяться внутри каждого ФМ слоя вдоль и против оси
. Из (6) следует, что число связанных волн при учете взаимодействия с соседним ФМ слоем увеличивается вдвое, таким образом, рассматриваемая структура аналогична системе двух связанных осцилляторов, собственная частота каждого из которых совпадает с частотой невзаимодействующих слоев. Следовательно, с увеличением числа слоев в структуре увеличивается и число связанных волн в каждом слое.
В НМП слоях распространяются невзаимодействующие ЭМВ вдоль и против оси
с законом дисперсии
,
где
,
– статическая проницаемость и электропроводность НМП прослойки.
3. Случай многослойной структуры
Как было показано выше, число связанных волн внутри ФМ слоев пропорционально количеству ФМ слоев в структуре. Также с ростом N уменьшается “прозрачность” слоистой структуры, поэтому представляет интерес дальнейший расчет проводить для случая структуры, состоящей из N ФМ слоев и N-1 НМП прослоек, находящихся между магнитными слоями. При этом учтем только взаимодействие между соседними слоями. Также предположим, что в нечетном магнитном слое намагниченность направлена по оси
, а в четном - в противоположном направлении. Число слоев в структуре с намагниченностью вдоль оси
равно числу слоев с намагниченностью против оси
(N – четно). Магнитную часть энергии многослойной структуры в расчете на единицу площади можно записать следующим образом [6]
Отметим, что, поскольку ФМ слой внутри структуры взаимодействует одновременно с двумя соседними ФМ слоями, а первый и последний ФМ слои взаимодействуют лишь с одним соседним ФМ слоем, то энергия межслойного взаимодействия первого и последнего слоев в два раза меньше, чем для внутренних слоев. С учетом этого для внутренних слоев в условии существования АФМ структуры (4) необходимо заменить J1-2J2 на 2(J1-2J2). Таким образом, условия существования равновесного состояния в крайних и внутренних ФМ слоях отличаются.
В общем случае аналитически получить дисперсионное уравнение многослойной структуры с N>2 невозможно, поэтому все расчеты для таких структур проводились только численно. Решением дисперсионного уравнения (6) относительно волнового числа являются 6N значений, соответствующих 3N связанным волнам, которые могут распространяться внутри каждого ФМ слоя вдоль и против оси
.
На поверхностях ФМ слоев должны выполняться условия непрерывности тангенциальных составляющих векторов напряженностей и нормальных компонент векторов индукции электрического и магнитного полей, а также равенство нулю производной намагниченности [3-5]. Пусть в области
распространяются падающая (
,
) и отраженная (
,
) волны, а в области
- прошедшая в полубесконечную немагнитную проводящую среду волна (
,
). Обозначим волны, распространяющиеся в n-ом магнитном слое, через
, где i=1¸3N для волн, распространяющихся вдоль нормали к поверхности структуры, i=(3N+1)¸6N для волн, распространяющихся в противоположном направлении, а в n-ом проводнике – через
и
соответственно. Для удобства исходную систему граничных условий преобразуем следующим образом. Для каждого ФМ слоя граничные условия, накладываемые на электромагнитное поле и намагниченность, на верхней границе слоя сложим (с положительным и отрицательным знаком соответственно) с граничными условиями, накладываемыми на электромагнитное поле и намагниченность, на нижней границе слоя. В этом случае система граничных условий для n-ого (n=1¸N) магнитного слоя может быть записана следующим образом.
Для
={hx(n),ey(n)}
где на верхней границе структуры
={h(0),e(0)},
={h(R),e(R)}, на внутренних границах
={
}, а на нижней границе
={h(T),e(T)},
=0.
Для
={mx(n),mz(n)}
индекс m в выражениях (9) и (10) указывает на параметры НМП слоя.
Выражая из линеаризованной системы связанных уравнений (5) компоненты намагниченности (mx(n), mz(n)) и напряженности электрического поля (ey(n)) через компоненты напряженности магнитного поля (hx(n)) и подставляя их в граничные условия (9) и (10), получим систему уравнений, содержащую только компоненты напряженности магнитного поля. Из данной системы при использовании корней дисперсионного уравнения (6) можно определить КО
и
- компоненты напряженности магнитного поля в n-ом ФМ слое.
Зная
, обратным путем из (5) можно рассчитать
,
и, следовательно, можно вычислить компоненты интегральной восприимчивости рассматриваемой структуры для каждого магнитного слоя
, определяемые как коэффициенты пропорциональности между компонентами интегральной намагниченности и компонентами внешнего магнитного поля (
) [10] и для всей структуры в целом
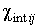
Расчет КО ЭМВ проводился численно. Сначала из дисперсионного уравнения (6) определялись волновые числа связанных волн, распространяющихся в ФМ слоях. Полученные значения волновых чисел подставлялись в систему граничных условий (9)-(10). Далее данная система решалась относительно амплитуды отраженной волны и по формуле (11) вычислялся КО. Для расчета интегральной восприимчивости находились компоненты напряженности магнитного поля внутри ФМ слоев, через них, используя систему связанных уравнений (5) для ФМ слоя, определялись компоненты намагниченности и по формуле (12) окончательно вычислялась интегральная магнитная восприимчивость структуры.
При численных расчетах для всех структур использовались следующие значения постоянных, типичных для проводящих ФМ кубической симметрии (ферритов):
,
,
,
;
,
см,
=2.5´1016 с-1 - для НМП слоя;
с-1 - для немагнитной полубесконечной проводящей среды. Постоянные межслойного взаимодействия во всех расчетах полагались следующими: J1 = - 0.5 эрг/см2, J2 = -0.15 эрг/см2 [6].
4. Обсуждение результатов
Отметим, что из (4) и (6) следует, что интенсивность влияния межслойного обменного взаимодействия на характеристики рассматриваемых структур зависит от толщины слоев. Поскольку при численных расчетах постоянные межслойного обменного взаимодействия J1,2 брались порядка -(0.1¸0.5) эрг/см3, то отсюда следует, что имеет смысл рассматривать только структуры с такими толщинами ФМ слоев, при которых межслойное взаимодействие сравнимо с магнитной анизотропией:
. Поэтому, при численных расчетах константа анизотропии полагалась равной К1=103 эрг/см3, а толщина всех слоев бралась равной l =10-4 см. В этом случае рассматриваемое основное состояние является устойчивым в полях
Э при отсутствии межслойного взаимодействия и в полях
Э » 6.9 Э при наличии межслойного взаимодействия.
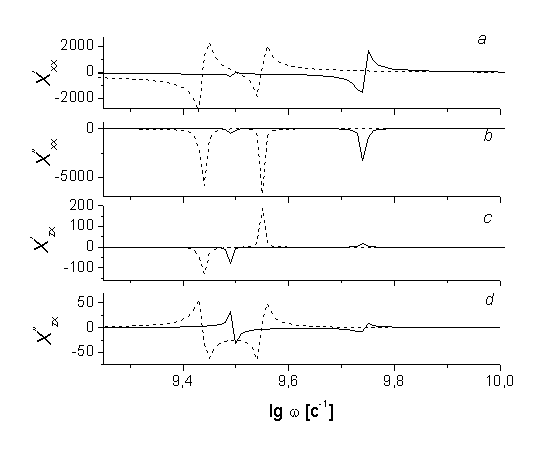
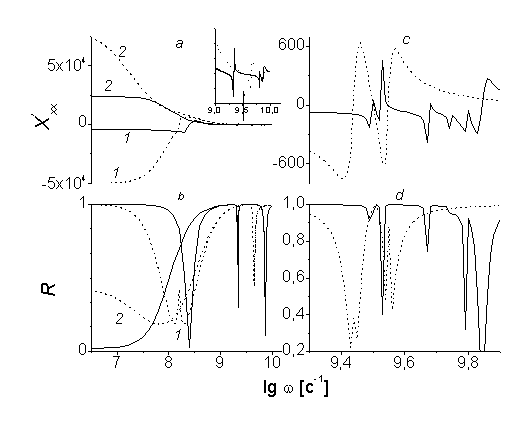
Частотные зависимости компонент интегральной восприимчивости трехслойной структуры при H=1 Э представлены на рис. 2. Из анализа дисперсионного уравнения (6) следует, что наблюдаемое на рис. 2 аномальное поведение интегральной восприимчивости на частотной зависимости имеет место в областях ФМ резонанса в магнитных слоях. В области остальных частот восприимчивость не испытывает никаких особенностей.
Рис. 2. Зависимость реальной и мнимой части компонент
(a, b) и
(c, d) интегральной восприимчивости от частоты. Здесь и далее сплошные кривые - зависимости для случая взаимодействующих (J1,2
0) слоев, а пунктирные кривые – зависимости для случая невзаимодействующих (J1,2=0) слоев. Магнитное поле H=1 Э Э, К1=103 эрг/см3,
с-1, N=2.
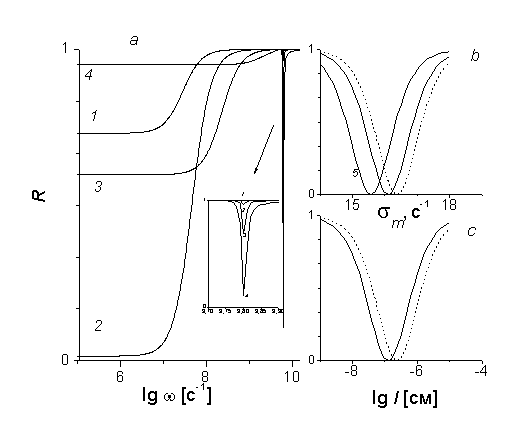
На рис. 3a. представлены зависимости КО от частоты при разных значениях электропроводности, на рис. 3b – от электропроводности, на рис. 3c - от толщины проводящего слоя в области ОФП структуры. Анализ частотной зависимости КО (рис. 3а) показывает, что при частотах меньших 107 с-1 КО минимален и практически не зависит от частоты. В этой области частот на зависимостях КО от электропроводности (рис. 3b) и толщины слоев (рис. 3c) наблюдаются отчетливо выраженные минимумы, что не имеет места на более высоких частотах. Это обусловлено тем, что при некотором соотношении электропроводности и толщины проводящего слоя (
) в области низких частот выполняется условие
, где
. На резонансах в области высоких частот (рис. 3а) КО тем меньше, чем выше электропроводность.
Рис. 3. Зависимость КО ЭМВ в точке ОФП: (a) -от частоты для различных значений электропроводности проводящих прослоек
: 1 –
с-1; 2 –
с-1; 3-
с-1; 4-
с-1 при l=10-4 см, N=2; (b) -от электропроводности
при ω =105 с-1, l=10-4, N=2 (5 – для N=8); (c)-от толщины ФМ слоев при ω =105 с-1,
с-1, N=2
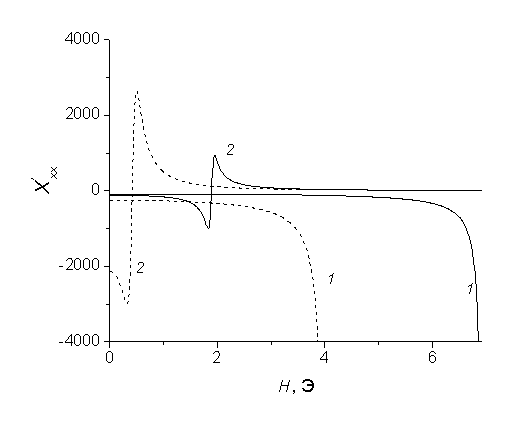
На рис. 4 показана полевая зависимость вещественной части компоненты
интегральной восприимчивости для двух значений частоты. Видно, что в области низких частот восприимчивость резонансно возрастает по модулю в области поля ОФП. При увеличении частоты резонанс смещается в область малых полей, таким образом, что при ещё больших частотах на полевой зависимости восприимчивости не проявляется никаких особенностей. Из рис. 4 также следует, что учет межслойного взаимодействия действительно приводит к смещению точки ОФП в область более сильных полей.
Рис. 4. Зависимость реальной части
компоненты интегральной восприимчивости от внешнего поля для различных частот: 1 – ω =108 с-1, 2 – ω =3´109 с-1 при К1=103 эрг/см3, l=10-4 см,
с-1 ,N=2.
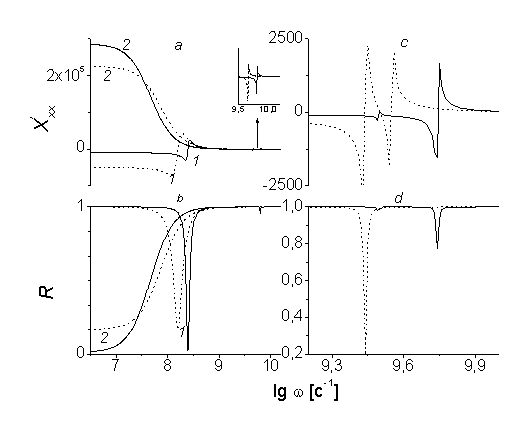
На рис. 5а, 5b приведены результаты численного расчета интегральной восприимчивости и КО для слоистой структуры (N=2) при К1=103 эрг/см3, l=1´10-4 см в области ОФП, а на рис 5с, 5d – при малом внешнем магнитном поле
Э. Напомним, что при таких значениях константы анизотропии и толщины слоев поле ОФП в четных ФМ слоях равно 4 Э и 6.9 Э соответственно при отсутствии и наличии межслойного взаимодействия. Из рис. 5 видно, что КО резко убывает в области аномального поведения интегральной восприимчивости, то есть в области ФМ резонансов в ФМ слоях. Также видно, что наличие межслойного взаимодействия приводит к смещению пиков КО. При приближении к точке ОФП (рис. 5) происходит смещение резонансной частоты четных ФМ слоев в сторону низких частот и уширение пика КО. Это приводит к тому, что вблизи ОФП при низких частотах КО равен нулю, то есть система превращается из полностью отражающей в полностью поглощающую.
Рис. 5. Зависимость реальной части
компоненты интегральной восприимчивости (a, c) и КО ЭМВ (b, d) от частоты для различных значений внешнего магнитного поля Н. a, b: 1 – вблизи ОФП 3.99 Э, пунктирная кривая (невзаимодействующие слои), 6.9 Э, сплошная кривая (взаимодействующие слои); 2 – в точке ОФП 4 Э, пунктирная кривая,
Э, сплошная кривая. c, d – 1 Э. К1=103 эрг/см3, l=10-4 см,
с-1 , N=2.
Для того, чтобы резонансные частотные области уменьшения КО были более широкие, необходимо увеличивать толщину слоистой структуры в целом. Это можно сделать несколькими способами.
Первый способ - увеличение числа слоев. При этом для значения постоянной анизотропии К1=103 эрг/см3 число слоев необходимо увеличить до 103-105. В данном случае из-за взаимодействия ФМ слоев резко увеличивается степень дисперсионного уравнения, что приводит к значительному увеличению времени расчетов.
Второй способ - увеличение толщины магнитного слоя. При этом уменьшается вклад в эффективную анизотропию структуры от межслойного взаимодействия. Для того, чтобы он оставался сравнимым с вкладом от анизотропии, необходимо уменьшать и постоянную магнитной анизотропии.
На рис. 6a, 6b приведен результат численного расчета интегральной восприимчивости и КО для многослойной структуры (N=8, К1=103 эрг/см3, l=10-4 см) в области ОФП, а на рис. 6с, 6d – при малом внешнем поле
Э. Отметим, что при таком значении константы анизотропии и толщины слоев поле ОФП при наличии межслойного взаимодействия в нижнем ФМ слое равно 6.9 Э, а для внутренних нечетных слоев поле ОФП имеет большее значение, поскольку, как говорилось выше, энергия межслойного взаимодействия первого и последнего слоев в два раза меньше внутренних. Из рис. 6 видно, что в данном случае число резонансных пиков при наличии межслойного взаимодействия увеличивается (ср. с рис. 5). Это обусловлено тем, что при равных толщинах поле ОФП в взаимодействующих слоях различно, а следовательно резонансы от разных ФМ слоев с одинаковым направлением намагниченности отличаются друг от друга по частоте.
Рис. 6. тоже, что на рис 5. при N=8.
5. Заключение
Таким образом, в настоящей работе теоретически исследовано влияние межслойного обменного взаимодействия на равновесное состояние, интегральную восприимчивость и отражательную способность структур, состоящих из взаимодействующих между собой ФМ слоев с АФМ направлением намагниченности относительно друг друга, разделенных НМП прослойками. Численно рассчитаны частотные и полевые зависимости интегральной восприимчивости и КО ЭМВ при различном числе слоев в структуре.
Показано, что область существования АФМ слоистой структуры во внешнем магнитном поле при наличии межслойного взаимодействия увеличивается. Интегральная восприимчивость и КО ЭМВ имеют резонансные особенности в области частот, отвечающих частотам ФМ резонанса в ФМ слоях. При этом при приближении к точке ОФП происходит смещение пика на частоте, отвечающей ФМ резонансу в слоях с противоположным по отношению к внешнему полю направлением намагниченности (четные слои), в область низких частот и его уширение. Это приводит к тому, что вблизи ОФП при низких частотах КО равен нулю, то есть система превращается из полностью отражающей в полностью поглощающую.
Увеличение числа слоев приводит к увеличению числа резонансных пиков КО и уширению некоторых из них, за счет наложения пиков друг на друга. Это обусловлено тем, что резонансы от ФМ слоев отличаются по частоте из-за различия величины межслойного взаимодействия для внешних и внутренних слоев. В области резонансов КО близок к нулю, то есть при резонансных частотах многослойная структура из полностью отражающей для ЭМВ рассматриваемого диапазона (108-1011 с-1) становится полностью поглощающей. Также показано, что учет межслойного взаимодействия приводит к смещению резонансных особенностей. Все это может представлять интерес с практической точки зрения при конструировании устройств, в которых необходимо смещать резонансные частоты или включать новые.
Работа выполнена при финансовой поддержке гранта РФФИ-Урал 07_02_96030.
Список литературы
[1] Казанцева Н.Е., Рывкина Н.Г., Чмутин И.А. // РЭ. 2003. Т. 48, №2, С. 196.
[2] Антонов А.С., Панина Л.В., Сарычев А.К. // ЖТФ. 1989. Т. 59, №6, С. 88,.
[3] Бучельников В.Д., Бычков И.В., Шавров В.Г. // ФТТ. 1992. Т. 34, №11, С. 3408.
[4] Бабушкин А.В., Бучельников В.Д., Бычков И.В. // ФТТ. 2002. Т. 44, №12, С. 2183.
[5] Бучельников В.Д., Бабушкин А.В., Бычков И.В. // ФТТ. 2003. Т. 45, №4, С. 663.
[6] Хусаинов М.Г. // ЖЭТФ. 1996. Т. 109, С. 524.
[7] Хусаинов М.Г. // ЖЭТФ. 1996. Т. 110, С. 966.
[8] Дровосеков А.Б., Жотикова О.В. и др. // ЖЭТФ. 1999. Т. 119, №5, С. 1817.
[9] Туров Е.А., Шавров В.Г. // УФН. 1983. Т. 140, №3, С. 429.
[10] Сукстанский А.Л., Ямпольская Г.И. // ФТТ. 2000. Т. 42, №5, С. 866.
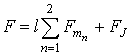
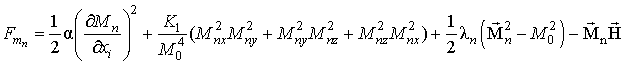 , (2)
, (2)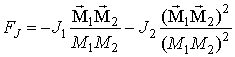 , (3)
, (3)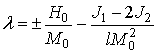 ,
, 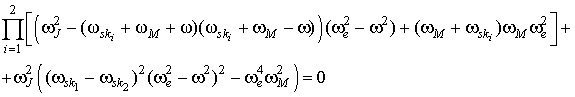 (6)
(6)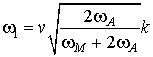 ,
,
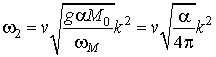 , (7)
, (7)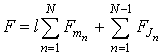
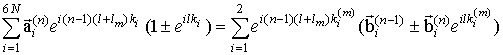 , (9)
, (9)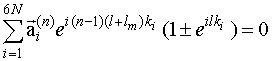 , (10)
, (10)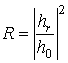 .
.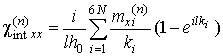 ,
,
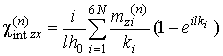 ,
,
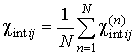 . (12)
. (12)