КВАЗИГИДРОДИНАМИЧЕСКОЕ МОДЕЛИРОВАНИЕ ОСОБЕННОСТЕЙ ЭЛЕКТРОПРОВОДНОСТИ НАНОРАЗМЕРНЫХ МНОГОСЛОЙНЫХ СИЛЬНОЛЕГИРОВАННЫХ ГЕТЕРОСТРУКТУР
В.А. Гергель, А.П. Зеленый, М.Н. Якупов
Институт
радиотехники и электроники РАН
Получена 19 марта 2007 г.
Методами математического моделирования на основе уравнения
энергетического баланса исследована электропроводность наноразмерных слоистых
гетероструктур в сильных электрических полях. Использовано
квазигидродинамическое описание электронного дрейфа с учетом диффузионной и
термодиффузионной компонент тока, дивергенции электронного теплового потока и
температурной зависимости подвижности и времени энергетической релаксации.
Полученные вольтамперные характеристики с высотой барьера ![]() и равной протяженностью узко- и
широкозонных составляющих
и равной протяженностью узко- и
широкозонных составляющих ![]() , в зависимости от уровня легирования в
диапазоне
, в зависимости от уровня легирования в
диапазоне ![]() отличает
либо резкий пик дифференциальной проводимости, либо, так называемая, петля
бистабильности, отвечающая термоинжекционной неустойчивости. Предложена
физическая модель, интерпретирующая форму расчетных характеристик кумулятивным
действием электростатического снижения высоты гетеробарьеров и ростом
электронной температуры в окрестности инжектирующих гетерограниц.
отличает
либо резкий пик дифференциальной проводимости, либо, так называемая, петля
бистабильности, отвечающая термоинжекционной неустойчивости. Предложена
физическая модель, интерпретирующая форму расчетных характеристик кумулятивным
действием электростатического снижения высоты гетеробарьеров и ростом
электронной температуры в окрестности инжектирующих гетерограниц.
Введение
В предыдущей работе авторов [1] методами математического моделирования на
основе уравнения энергетического баланса исследовалась электропроводность наноразмерных слоистых сильнолегированных гетероструктур в сильных электрических
полях. В ней было показано, что характерной особенностью соответствующих
вольтамперных характеристик является сильная нелинейность и пик
дифференциальной проводимости при значениях токов порядка ![]()
![]() , где
, где ![]() - концентрация легирующей примеси, а
- концентрация легирующей примеси, а ![]() - скорость насыщения.
Абсолютная величина этого пика и его положения на оси напряжений оказались
зависящими от высоты и крутизны гетеробарьеров, равно как и от уровня легирования.
Предложенная нами в [1] физическая модель интерпретировала отмеченные
особенности рассчитанных токовых характеристик, кумулятивным действием
электростатического снижения высоты гетеробарьеров, возникающего вследствие
конечной протяженности области резкого изменения состава на гетерограницах и
нарастанием электронной температуры в окрестности инжектирующих гетерограниц с
увеличением тока. Следует сказать, что указанные физические механизмы,
изначально заложенные в расчетные процедуры работы [1] использованием: квазигидродинамического описания электронного дрейфа (1) и непрерывным
представлением пространственных изменений зонного квазипотенциала (2), в
принципе должны обеспечивать и возникновения бистабильных (S-образных)
участков вольтамперных характеристик, отвечающих, как мы ее будем называть в
дальнейшем, термоинжекционной неустойчивости. Поскольку, ожидаемая
бистабильность вольтамперных характеристик легированных сверхрешеток достаточно
интересна, как с чисто физической точки зрения, так и с точки зрения возможных
технических применений, изучение соответствующих закономерностей методами
численного моделирования и составило цель настоящей работы.
- скорость насыщения.
Абсолютная величина этого пика и его положения на оси напряжений оказались
зависящими от высоты и крутизны гетеробарьеров, равно как и от уровня легирования.
Предложенная нами в [1] физическая модель интерпретировала отмеченные
особенности рассчитанных токовых характеристик, кумулятивным действием
электростатического снижения высоты гетеробарьеров, возникающего вследствие
конечной протяженности области резкого изменения состава на гетерограницах и
нарастанием электронной температуры в окрестности инжектирующих гетерограниц с
увеличением тока. Следует сказать, что указанные физические механизмы,
изначально заложенные в расчетные процедуры работы [1] использованием: квазигидродинамического описания электронного дрейфа (1) и непрерывным
представлением пространственных изменений зонного квазипотенциала (2), в
принципе должны обеспечивать и возникновения бистабильных (S-образных)
участков вольтамперных характеристик, отвечающих, как мы ее будем называть в
дальнейшем, термоинжекционной неустойчивости. Поскольку, ожидаемая
бистабильность вольтамперных характеристик легированных сверхрешеток достаточно
интересна, как с чисто физической точки зрения, так и с точки зрения возможных
технических применений, изучение соответствующих закономерностей методами
численного моделирования и составило цель настоящей работы.
Отметив, что
впервые предположение о принципиальной возможности существования S-образного участка вольтамперных характеристик легированных
сверхрешеток было высказано Р.А. Сурисом и В.А. Федирко в известной работе [2],
посвященной исследованию разогревной фотопроводимости и соответствующей
чувствительности легированных сверхрешеток к мощности внешнего СВЧ излучения,
рассмотрим предварительно достаточно упрощенную ситуацию, отвечающую отсутствию
легирующих примесей в широкозонных составляющих сверхрешетки, когда нам удастся
получить аналитическое выражение для соответствующей S-образности,
используя обычное, так называемое, дрейфово-диффузионное приближение (ДДМ) [3].
Можно полагать, что такое сильно упрощенное рассмотрение облегчит понимание
приведенных далее результатов численного моделирования отвечающих строгой
постановке задачи.
1. Элементарная модель неустойчивости
Схематически, элементарное звено такой упрощенной селективно легированной
сверхрешетки изображено на врезке рис.1, и представляет собой комбинацию
резистивного (узкозонного) элемента (![]() ) и широкозонного емкостного (
) и широкозонного емкостного (![]() ) элемента с “утечкой”,
определяемой надбарьерной инжекцией [4]. Ясно, что соотношение значений
электрических полей
) элемента с “утечкой”,
определяемой надбарьерной инжекцией [4]. Ясно, что соотношение значений
электрических полей ![]() и
и
![]() в резистивной
и емкостной области при наличии внешнего напряжения
в резистивной
и емкостной области при наличии внешнего напряжения ![]() на рассматриваемой ячейке
определяется равенством тока проводимости в узкозонной части и надбарьерного
тока в широкозонную область
на рассматриваемой ячейке
определяется равенством тока проводимости в узкозонной части и надбарьерного
тока в широкозонную область
где ![]() - скорость насыщения,
- скорость насыщения, ![]() -тепловая скорость,
-тепловая скорость, ![]() -подвижность, а
-подвижность, а
- максимальная
концентрация электронов в обогащенном слое у гетерограницы, индуцирующем
соответствующую разность полей в емкостном и резистивном элементах
рассматриваемой структуры. Из левой части (1), представляющей собой простейшую
форму описания эффекта насыщения дрейфовой скорости в предположении локальности
разогрева электронного газа, когда электронная температура ![]() , находим
, находим
где ![]() - безразмерная плотность
тока, а
- безразмерная плотность
тока, а ![]() -
равновесная температура. Теперь переписав правую часть (1) с учетом (2,3)
-
равновесная температура. Теперь переписав правую часть (1) с учетом (2,3)
где ![]() - численный коэффициент
порядка единицы, и извлекая квадратный корень, получим искомое аналитическое
выражение для вольтамперной характеристики
- численный коэффициент
порядка единицы, и извлекая квадратный корень, получим искомое аналитическое
выражение для вольтамперной характеристики
где ![]() - характерное
напряжение порядка вольта при
- характерное
напряжение порядка вольта при ![]() ,
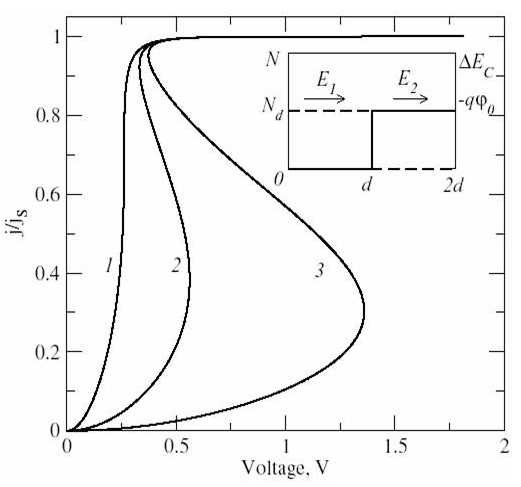
, ![]() . Отвечающие уравнению (5) графики
вольтамперных характеристик приведенные на рис.1 для значений параметра
. Отвечающие уравнению (5) графики
вольтамперных характеристик приведенные на рис.1 для значений параметра ![]() демонстрируют ожидаемую
S-образность. Разумеется, приведенная выше крайне
упрощенная аналитическая модель и графики рис.1 не претендуют на сколь-нибудь
разумную количественную точность описания рассматриваемого эффекта
отрицательного дифференциального сопротивления, а предназначена лишь для
облегчения понимания его природы, выявляя соответствующую положительную обратную
связь, глубина которой определяется отношением высоты энергетического
гетеробарьера
демонстрируют ожидаемую
S-образность. Разумеется, приведенная выше крайне
упрощенная аналитическая модель и графики рис.1 не претендуют на сколь-нибудь
разумную количественную точность описания рассматриваемого эффекта
отрицательного дифференциального сопротивления, а предназначена лишь для
облегчения понимания его природы, выявляя соответствующую положительную обратную
связь, глубина которой определяется отношением высоты энергетического
гетеробарьера ![]() к
равновесной тепловой энергии
к
равновесной тепловой энергии ![]() .
.
Рис.1. Вольтамперные характеристики упрощенной селективно
легированной сверхрешетки для значений параметра ![]() : 1 – 2, 2 – 4, 3 –
6.
: 1 – 2, 2 – 4, 3 –
6.
2. Строгая постановка задач моделирования
Приступим теперь к изложению результатов исследования рассматриваемого эффекта бистабильности на основе значительно более строгого, так называемого, квазигидродинамического описания дрейфового процесса [1,5], где уравнения Пуассона и непрерывности
дополнены уравнением энергетического баланса [5]
Систему (6,7) раскрывают формулы для электронного потока
и потока электронной температуры
выписанные при упрощающем предположении о степенном характере зависимостей подвижности и времени энергетической релаксации от температуры
где ![]() - равновесная
температура,
- равновесная
температура, ![]() -
низкополевая подвижность, а значение
-
низкополевая подвижность, а значение ![]() согласовано с величиной, так называемой,
скорости насыщения
согласовано с величиной, так называемой,
скорости насыщения ![]() .
Ниже, ориентируясь на гетероструктуры на основе GaAs,
для постоянных
.
Ниже, ориентируясь на гетероструктуры на основе GaAs,
для постоянных ![]() ,
,
![]() и
и ![]() мы будем использовать
численные значения
мы будем использовать
численные значения ![]() ,
,
![]() ,
, ![]() . Отметим, что как и в
[1] в уравнениях (6-9) фигурирует описывающий энергетические барьеры, так
называемый, зонный квазипотенциал
. Отметим, что как и в
[1] в уравнениях (6-9) фигурирует описывающий энергетические барьеры, так
называемый, зонный квазипотенциал ![]() , где
, где ![]() - край зоны проводимости, изменяющийся с
координатой в соответствии с изменениями состава. При этом, однако, для
простоты, мы будем пренебрегать возможной зависимостью подвижности
- край зоны проводимости, изменяющийся с
координатой в соответствии с изменениями состава. При этом, однако, для
простоты, мы будем пренебрегать возможной зависимостью подвижности ![]() от состава. В качестве
шага сверхрешетки выберем довольно большую величину
от состава. В качестве
шага сверхрешетки выберем довольно большую величину ![]() нм, исключающую существенные
проявления туннельных явлений. Что же касается концентрации доноров
нм, исключающую существенные
проявления туннельных явлений. Что же касается концентрации доноров ![]() , мы будем предполагать
ее однородной. Отметим также, что для представления периодически изменяющегося
зонного квазипотенциала
, мы будем предполагать
ее однородной. Отметим также, что для представления периодически изменяющегося
зонного квазипотенциала ![]() , вместо обычно применяемых
кусочно-линейных аппроксимаций, мы сконструировали на основе известной функции
Ферми удобную вспомогательную функцию
, вместо обычно применяемых
кусочно-линейных аппроксимаций, мы сконструировали на основе известной функции
Ферми удобную вспомогательную функцию
которая с ростом
![]() из постоянной
из постоянной ![]() при
при ![]() превращается в сколь угодно
резкий меандр с амплитудой
превращается в сколь угодно
резкий меандр с амплитудой ![]() и максимальной производной на
гетерограницах
и максимальной производной на
гетерограницах ![]() при
соответствующем значении этого параметра. Помимо того, что распределение (11)
непрерывно сшивается с постоянными
при
соответствующем значении этого параметра. Помимо того, что распределение (11)
непрерывно сшивается с постоянными ![]() , что позволяет сформировать
соответствующие контактные области после требуемого числа периодов изменения
, что позволяет сформировать
соответствующие контактные области после требуемого числа периодов изменения ![]() , главное его достоинство
состоит в том, что оно позволяет сконструировать эффективный итерационный
процесс вычислений, стартуя от соответствующих распределений концентраций,
потенциала и температуры при требуемом значении приложенного напряжении
, главное его достоинство
состоит в том, что оно позволяет сконструировать эффективный итерационный
процесс вычислений, стартуя от соответствующих распределений концентраций,
потенциала и температуры при требуемом значении приложенного напряжении ![]() в однородной структуре
в однородной структуре ![]() , а затем
последовательно наращивать величину параметра
, а затем
последовательно наращивать величину параметра ![]() до его конечного значения
до его конечного значения ![]() , определяемого
актуальной резкостью краев гетероструктуры. Типичный график использованного представления
, определяемого
актуальной резкостью краев гетероструктуры. Типичный график использованного представления
![]() с параметрами
с параметрами
![]() В и
В и ![]() приведен на
рис.2.
Ясно, что в ситуациях с определенным уровнем легирования широкозонных областей
сверхрешетки, в ее отдельных звеньях происходит соответствующее
перераспределение электронной плотности, вырабатывается специфический
встроенный потенциал и возникает соответствующее чередование обедненных и
обогащенных слоев, отвечающих классическим представлениям Андерсона и Чанга
[6,7] об электростатике гетеробарьеров. Соответствующий результирующий
энергетический профиль однородно легированной сверхрешетки с
приведен на
рис.2.
Ясно, что в ситуациях с определенным уровнем легирования широкозонных областей
сверхрешетки, в ее отдельных звеньях происходит соответствующее
перераспределение электронной плотности, вырабатывается специфический
встроенный потенциал и возникает соответствующее чередование обедненных и
обогащенных слоев, отвечающих классическим представлениям Андерсона и Чанга
[6,7] об электростатике гетеробарьеров. Соответствующий результирующий
энергетический профиль однородно легированной сверхрешетки с ![]() представлен кривой 2
на рис.2. Важно отметить, что в рассматриваемых ситуациях гетеробарьеров
конечной крутизны, истинная высота гетеробарьера, складывающаяся в
противоборстве электрического поля обедненного слоя и исходного квазиполя
реальной гетерограницы, оказывается существенно меньше исходного значения
представлен кривой 2
на рис.2. Важно отметить, что в рассматриваемых ситуациях гетеробарьеров
конечной крутизны, истинная высота гетеробарьера, складывающаяся в
противоборстве электрического поля обедненного слоя и исходного квазиполя
реальной гетерограницы, оказывается существенно меньше исходного значения ![]() . В представленном на
рис.2 примере с
. В представленном на
рис.2 примере с ![]() В,
В,
![]() и
и ![]() , такое уменьшение
составляет
, такое уменьшение
составляет ![]() В.
С ростом
В.
С ростом ![]() оно
будет увеличиваться, а с ростом крутизны – уменьшаться.
оно
будет увеличиваться, а с ростом крутизны – уменьшаться.
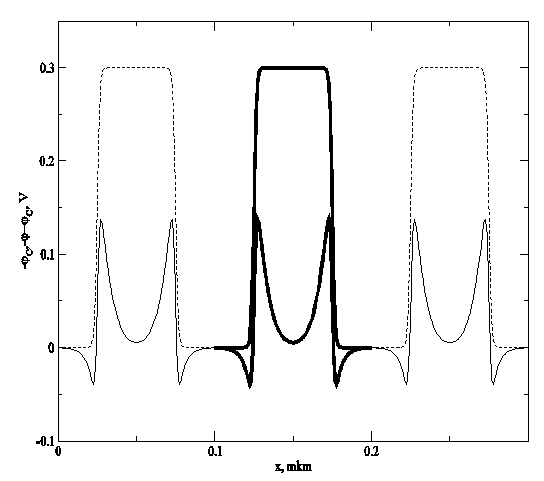
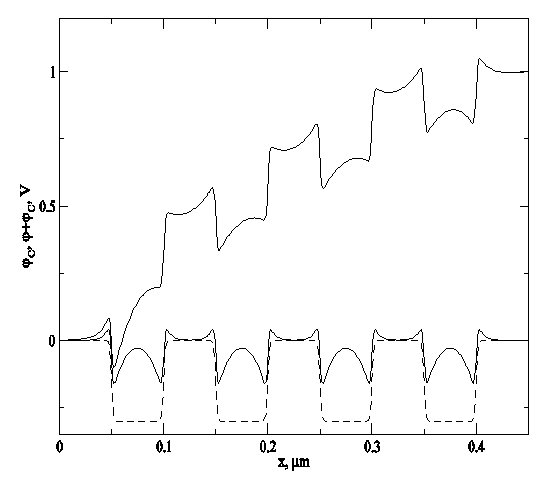
Рис.2. Пространственное распределение зонного квазипотенциала ![]() и действующего
потенциала
и действующего
потенциала ![]() при
нулевом приложенном напряжении
при
нулевом приложенном напряжении
4.
Моделирование электроразогревного процесса в элементарном звене сверхрешетки
Соответствующие
численные эксперименты применительно к достаточно протяженным сверхрешеткам
начнем с изучения электроразогревного процесса в каком-либо ее типичном
элементарном звене, в качестве которой оказалось удобным выбрать широкозонный
слой в окружении двух половинок соответствующих узкозонных слоев (жирная линия
на рис.2, ![]() мкм).
Ясно, что граничными условиями такой задачи, являются условия "сшивки"
соответствующих распределений температуры и концентраций на границах
элементарных ячеек
мкм).
Ясно, что граничными условиями такой задачи, являются условия "сшивки"
соответствующих распределений температуры и концентраций на границах
элементарных ячеек
и
При этом для потенциала, как обычно,
где ![]() - удельное напряжение на
ячейку, поскольку необходимое равенство производных
- удельное напряжение на
ячейку, поскольку необходимое равенство производных ![]() автоматически вытекает из
электронейтральности ячейки, обеспечиваемой граничными условиями на
концентрацию (12).
автоматически вытекает из
электронейтральности ячейки, обеспечиваемой граничными условиями на
концентрацию (12).
Относительно
особенностей численного моделирования системы базисных уравнений (6,
7) следует
сказать, что для ее дискретизации использовался модифицированный метод Шарфеттера-Гумеля [8] и стандартный метод Ньютона, обеспечивающий построение
соответствующих решений при фиксированном ![]() и произвольных (но равных друг другу)
значениях граничных концентраций и температур. Затем в действие вступает
итерационный процесс изменения этих граничных значений обеспечивающий
минимизацию разности соответствующих производных, т.е. выполнения квазициклических
граничных условий (12, 13).
и произвольных (но равных друг другу)
значениях граничных концентраций и температур. Затем в действие вступает
итерационный процесс изменения этих граничных значений обеспечивающий
минимизацию разности соответствующих производных, т.е. выполнения квазициклических
граничных условий (12, 13).
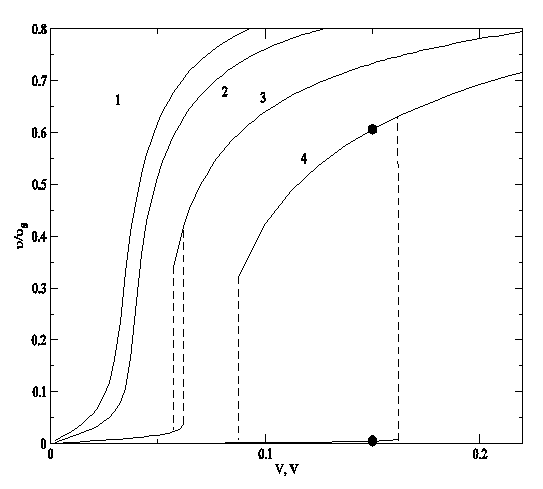
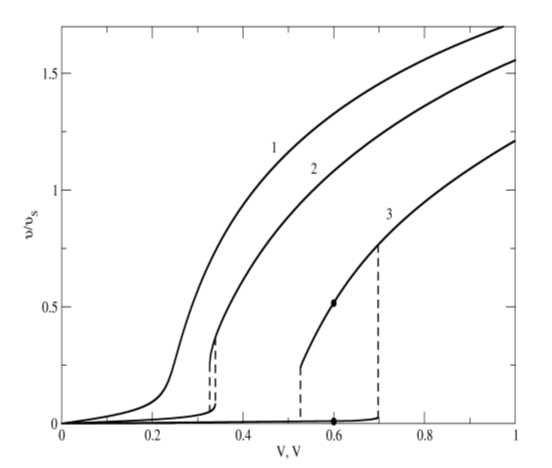
Рис.3. Вольтамперные характеристики элементарной ячейки при
различных уровнях легирования сверхрешетки ![]() : 1 –
: 1 – ![]() , 2 –
, 2 – ![]() , 3 –
, 3 – ![]() , 4 –
, 4 – ![]()
Типичный
пример расчетных вольтамперных характеристик рассматриваемых элементарных
ячеек, отличающихся лишь уровнем легирования, приведен на рис.3 в относительных
координатах ![]() .
Первые две кривые, отвечающие сравнительно высоким концентрациям
.
Первые две кривые, отвечающие сравнительно высоким концентрациям ![]() , и соответственно
более низким значением результирующей высоты энергетического барьеров,
демонстрируют ожидаемый довольно резкий (но непрерывный) переход от
сравнительно малых значениях тока к существенно большим, где скорость
электронного дрейфа близка к скорости насыщения. Иными словами кривые 1, 2
демонстрируют резкий пик дифференциальной проводимости обусловленный
"включением" термоинжекции, который с понижением уровня легирования – кривые 3
и 4 отвечающие
, и соответственно
более низким значением результирующей высоты энергетического барьеров,
демонстрируют ожидаемый довольно резкий (но непрерывный) переход от
сравнительно малых значениях тока к существенно большим, где скорость
электронного дрейфа близка к скорости насыщения. Иными словами кривые 1, 2
демонстрируют резкий пик дифференциальной проводимости обусловленный
"включением" термоинжекции, который с понижением уровня легирования – кривые 3
и 4 отвечающие ![]() (более
высокие барьеры) переходит в искомую петлю бистабильности. Заметим, что, строго
говоря, кривые 3, 4 состоят из двух отдельных перекрывающихся участков
отвечающих сравнительно большим и сравнительно малым значениям тока. Нижние
кривые получены использованием стандартного алгоритма численного моделирования
ВАХ, когда итерационный процесс отыскания тока в следующей точке оси напряжений
(более
высокие барьеры) переходит в искомую петлю бистабильности. Заметим, что, строго
говоря, кривые 3, 4 состоят из двух отдельных перекрывающихся участков
отвечающих сравнительно большим и сравнительно малым значениям тока. Нижние
кривые получены использованием стандартного алгоритма численного моделирования
ВАХ, когда итерационный процесс отыскания тока в следующей точке оси напряжений
![]() , где
, где ![]() - соответствующая дискрета,
стартует от уже известных распределений температуры и концентрации отвечающих
предыдущему значению напряжения. Достигнув точки потери устойчивости
- соответствующая дискрета,
стартует от уже известных распределений температуры и концентрации отвечающих
предыдущему значению напряжения. Достигнув точки потери устойчивости ![]() , программа делает
сравнительно большой шаг вперед по напряжению
, программа делает
сравнительно большой шаг вперед по напряжению ![]() , а затем, используя дополнительную
итерационную процедуру по
, а затем, используя дополнительную
итерационную процедуру по ![]() , выходит в соответствующую точку
сильнотокового участка ВАХ, который восстанавливает, двигаясь по оси напряжений
вниз (
, выходит в соответствующую точку
сильнотокового участка ВАХ, который восстанавливает, двигаясь по оси напряжений
вниз (![]() ), до
точки
), до
точки ![]() , где
итерационный процесс снова перестает сходиться. Имея в виду полученный ранее
аналитический результат для упрощенной модели (формула (5),
рис.1) не вызывает
сомнения, что в области
, где
итерационный процесс снова перестает сходиться. Имея в виду полученный ранее
аналитический результат для упрощенной модели (формула (5),
рис.1) не вызывает
сомнения, что в области ![]() в принципе должен существовать и
соответствующий неустойчивый участок ВАХ с отрицательным сопротивлением,
который однако не может быть выявлен нашими итерационными методами.
в принципе должен существовать и
соответствующий неустойчивый участок ВАХ с отрицательным сопротивлением,
который однако не может быть выявлен нашими итерационными методами.
Физическую
картину обнаруженного эффекта бистабильности ВАХ иллюстрируют графики на
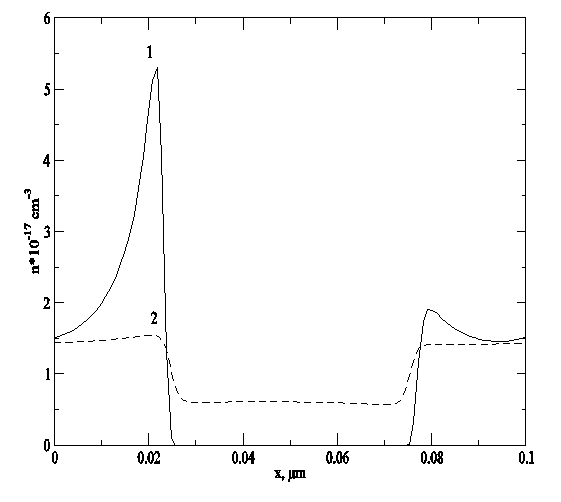
рис.4,5,6, где приведены типичные пространственные распределения концентрации,
температуры и действующего потенциала в типичных точках слабо- и сильнотокового
участков характеристики отмеченных на рис.3 жирными кружочками. Отвечающие
одному и тому же значению напряжения на исследуемой ячейке распределения
температур и концентраций существенно более однородны на верхней кривой,
отвечающей сильному электроразогреву и значительной (![]() ) инжекции горячих электронов в
широкозонную область, в то время как на нижнем участке практически все
электроны сосредоточены в обогащенных слоях узкозонных подобластей на границах
с широкозонной, а незначительный электронный разогрев в широкозонном слое почти
полностью компенсируется остыванием за счет терморелаксации в решетку в узкозонных
подобластях. Соответственно, и электростатический потенциал и его производная
более однородно распределены по ячейке в высокотемпературных ситуациях верхней
кривой.
) инжекции горячих электронов в
широкозонную область, в то время как на нижнем участке практически все
электроны сосредоточены в обогащенных слоях узкозонных подобластей на границах
с широкозонной, а незначительный электронный разогрев в широкозонном слое почти
полностью компенсируется остыванием за счет терморелаксации в решетку в узкозонных
подобластях. Соответственно, и электростатический потенциал и его производная
более однородно распределены по ячейке в высокотемпературных ситуациях верхней
кривой.
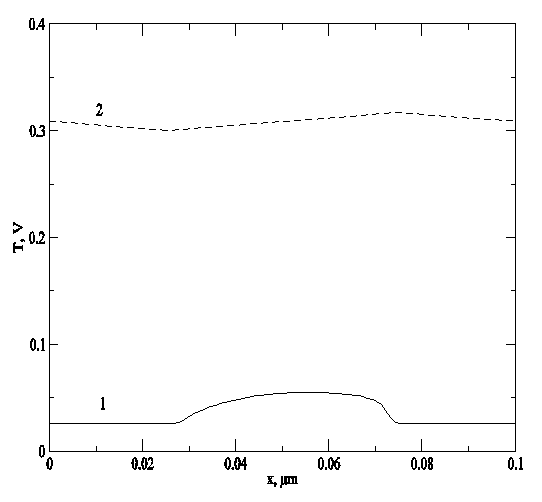
Рис.4. Пространственные распределения температуры в элементарной ячейке, соответствующие жирным кружочкам на рис.3
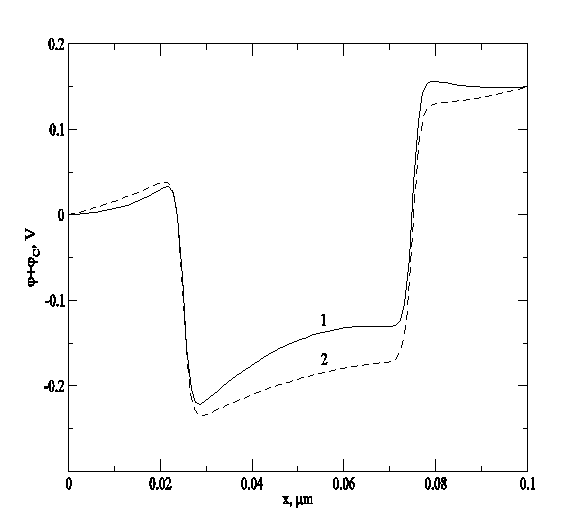
Рис.5. Пространственные распределения действующего потенциала в элементарной ячейке, соответствующие жирным кружочкам на рис.3
Рис.6. Пространственные распределения концентрации в элементарной ячейке, соответствующие жирным кружочкам на рис.3
Проведенный
анализ тенденций изменения характера пространственных зависимостей потенциала,
концентрации и электронной температуры вдоль ячейки с изменением напряжения
позволяет уточнить качественную физическую картину рассматриваемого дрейфового
процесса. При сравнительно малых напряжениях, отвечающих начальному участку
ВАХ, большая часть внешнего напряжения оказывается приложенной к обедненной
широкозонной области, где происходит соответствующий разогрев электронов.
Попав в узкозонный слой электроны остывают практически почти полностью до
равновесной температуры ![]() . При этом определяющим механизмом
формирования тока является надбарьерная термоинжекция, которая увеличивается с
ростом напряжения за счет увеличения концентрации в обогащенном слое на
гетерогранице и электростатического снижения энергетического барьера. С
дальнейшим ростом напряжения разогрев электронов в широкозонной части
усиливается, а охлаждение в узкозонной ослабевает, температура на гетерогранице
растет, инжекционный ток увеличивается и структура резко или "скачком"
переходит в сильнотоковое состояние, где тепловая энергия близка к значениям
высоты барьера, а величина тока лимитируется термодеградацией подвижности, т.е.
обычным эффектом насыщения дрейфовой скорости.
. При этом определяющим механизмом
формирования тока является надбарьерная термоинжекция, которая увеличивается с
ростом напряжения за счет увеличения концентрации в обогащенном слое на
гетерогранице и электростатического снижения энергетического барьера. С
дальнейшим ростом напряжения разогрев электронов в широкозонной части
усиливается, а охлаждение в узкозонной ослабевает, температура на гетерогранице
растет, инжекционный ток увеличивается и структура резко или "скачком"
переходит в сильнотоковое состояние, где тепловая энергия близка к значениям
высоты барьера, а величина тока лимитируется термодеградацией подвижности, т.е.
обычным эффектом насыщения дрейфовой скорости.
5. Сверхрешетки с конечным числом барьеров
Обратимся
наконец, к изучению более приближенной к реальной ситуациям модели легированной
сверхрешетки конечных размеров с четырьмя (для определенности) барьерами. Ясно,
что при этом следует использовать стандартный тип граничных условий ![]() и
и ![]() на ее внешних границах с
контактными областями, вместо квазициклических (12,
13). Результаты
соответствующего численного эксперимента по расчету ВАХ такой четырехбарьерной
структуры при значениях концентрации
на ее внешних границах с
контактными областями, вместо квазициклических (12,
13). Результаты
соответствующего численного эксперимента по расчету ВАХ такой четырехбарьерной
структуры при значениях концентрации ![]() продемонстрировали существенно более
плавные кривые по сравнению с характеристиками "типичной" ячейки, приведенными
на рис.3, а главное – полное отсутствие ожидаемой бистабильности. Конкретная
форма этих зависимостей практически полностью эквивалентна характеристикам
рассчитанным нами для аналогичной структуры в предыдущей работе ([1], рис.3) и
поэтому из "экономии" здесь не приводится. Вместо этого на следующем
рис.7
приведены пространственные распределения действующего потенциала
продемонстрировали существенно более
плавные кривые по сравнению с характеристиками "типичной" ячейки, приведенными
на рис.3, а главное – полное отсутствие ожидаемой бистабильности. Конкретная
форма этих зависимостей практически полностью эквивалентна характеристикам
рассчитанным нами для аналогичной структуры в предыдущей работе ([1], рис.3) и
поэтому из "экономии" здесь не приводится. Вместо этого на следующем
рис.7
приведены пространственные распределения действующего потенциала ![]() при нескольких типичных
значениях внешнего напряжения приложенного к такой четырехбарьерной структуре.
Эти графики, равно как и соответствующие распределения температур и
концентраций демонстрируют специфическую особенность термоинжекции на первом
гетеробарьере, где электронная температура в существенной степени наследуя
равновесную температуру контактной области, оказывается значительно меньше чем
на последующих гетерограницах. Поэтому доля внешнего напряжения на первом звене
сверхрешетки оказалась значительно превышающей падения напряжения на ее
последующих звеньях, что и блокировало реализацию искомых неустойчивостей.
при нескольких типичных
значениях внешнего напряжения приложенного к такой четырехбарьерной структуре.
Эти графики, равно как и соответствующие распределения температур и
концентраций демонстрируют специфическую особенность термоинжекции на первом
гетеробарьере, где электронная температура в существенной степени наследуя
равновесную температуру контактной области, оказывается значительно меньше чем
на последующих гетерограницах. Поэтому доля внешнего напряжения на первом звене
сверхрешетки оказалась значительно превышающей падения напряжения на ее
последующих звеньях, что и блокировало реализацию искомых неустойчивостей.
Рис.7. Пространственное распределение действующего потенциала ![]() в четырехбарьерной
структуре при приложенном напряжении
в четырехбарьерной
структуре при приложенном напряжении ![]() В и
В и ![]() В
В
Отмеченная
доминирующая роль первого звена сверхрешетки в формировании ВАХ представляет на
наш взгляд широкий спектр возможностей управлять формой ВАХ посредством внешних
электрических и радиационных воздействий, а также разнообразных структурных
модификаций "входного" звена. Возможности такого рода специализированных
структурных модификаций демонстрируют графики рис.8, полученные для структуры,
отличающейся от предыдущей лишь пониженной (0.2 вместо 0.3 эВ) высотой первого
гетеробарьера. Они показывают, что соответствующее облегчение термоинжекции и
последующий электроразогрев в этом пониженном гетеробарьере с успехом выявляет
главную особенность электрических свойств присущую последующим звеньям
сверхрешетки, а именно, искомую неустойчивость и соответствующую бистабильность
ВАХ. В заключение, учитывая сравнительную технологическую простоту изготовления
такого рода гетероструктур с бистабильными вольтамперными характеристиками,
можно предположить достаточнцю перспективность их использования для построения
устройств регистрации и генерации СВЧ излучения терагерцового диапазона. В этой
связи приведем также расчетные ВАХ гетерструктур с ![]() , в которых за первым
разогревающим барьером (0.2 эВ) следуют: один, три или пять основных барьеров
по 0.3 эВ (рис.9).
, в которых за первым
разогревающим барьером (0.2 эВ) следуют: один, три или пять основных барьеров
по 0.3 эВ (рис.9).
Рис.8. Вольтамперные характеристики четырехбарьерной структуры
при пониженной высоте первого гетеробарьера “1+3”: 1 - ![]() , 2 -
, 2 - ![]() , 3 -
, 3 - ![]()
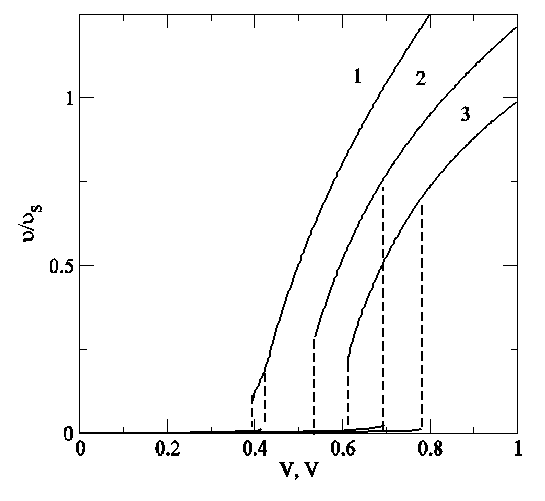
Рис.9. Вольтамперные характеристики гетероструктур с различным числом основных гетеробарьеров: 1 – “1+2”, 2- “1+3”, 3 – “1+4”.
Авторы считают своим приятным долгом выразить член.корр.РАН Р.А.Сурису благодарность за интерес к этой работе и плодотворные дискуссии, а также Российскому фонду фундаментальных исследований, при поддержке которого настоящая работа выполнена (РФФИ проект №04-02-17681).
Список литературы
[1] В.А. Гергель, В.А. Курбатов и М.Н. Якупов. ФТП 40(4), 446(2006)
[2] Р.А. Сурис, В.А. Федирко. ФТП 12(6), 1060 (1978)
[3] С.М. Зи. Физика полупроводниковых приборов, (М., Мир, 1984) Т1 с.54
[4] Г.Е. Пикус. Основы теории полупроводниковых приборов. (М. Наука, 1965) с.72
[5] R. Stratton. Phys. Rev., 126(6), 2002 (1962)
[6] R.L. Anderson. Sol.St.Electron., 5, 341 (1962)
[7] L.L. Chang. Sol.St.Electron., 8, 821 (1965)
[8] A. Forghieri, R. Guerrieri, P.Ciampolini, A. Gnudi and M. Rudan. IEEE Tran. On CAD, 7(2), 231(1988)
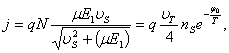 (1)
(1)
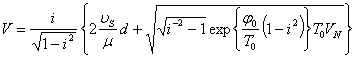 ,
(5)
,
(5)
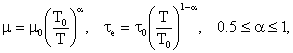 (10)
(10) ,
(11)
,
(11)