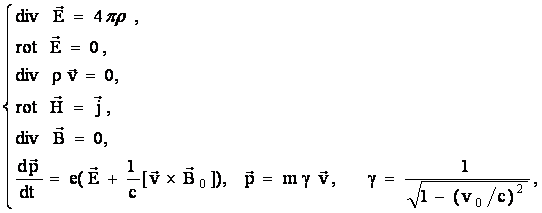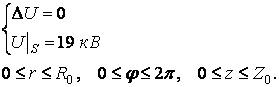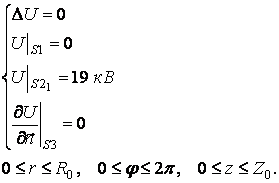|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 3, 2007 |
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ МНОГОЛУЧЕВОЙ ЭЛЕКТРОННОЙ ПУШКИ
В КИНЕМАТИЧЕСКОМ РЕЖИМЕ
С. В. Козлов, В.М. Пикунов, А.Н. Сандалов
Московский
государственный университет им. М.В. Ломоносова, физический факультет
Получена 15 марта 2007 г.
Приведены результаты численного моделирования многолучевой электронной пушки (МЛЭП) мощного многорезонаторного клистронного усилителя. Даны основные формулы и обсуждаются методы расчета электромагнитных полей для анализа электронно-оптических систем клистронных усилителей в трехмерном приближении. Определена погрешность метода. Представлены первые результаты расчетов многолучевой электронной пушки в кинематическом режиме: распределение электрического поля в пролетных каналах пушки, вид траекторий движения электронных пучков, значения токов и первеансов пучков. Обнаружены трехмерные эффекты, которые невозможно выявить с помощью двумерных программ: не аксиально-симметричный вид структуры силовых линий электрического поля, различие в значениях токов у электронных пучков.
Введение
При разработке мощных СВЧ приборов проводится моделирование физических процессов, происходящих внутри проектируемого устройства, с целью оптимизации эксплуатационных параметров. Для моделирования однолучевых клистронных усилителей, имеющих аксиально-симметричную структуру, были разработаны двумерные программные комплексы такие, как Арсенал-МГУ [1], EGUN [2], TOPAZ2D [3] и др.
Стремление получить высокое значение КПД и расширить полосу усиливаемых частот приборов привело к появлению многолучевых клистронов (МЛК) [4]. Так как высокое значение КПД клистронного усилителя достигается при малых значениях микропервеанса луча [5, 6], то необходимо либо увеличивать ускоряющее напряжение, что может привести к пробоям, либо уменьшать ток пучка, что снизит получаемую мощность. Данное противоречие решается использованием МЛК. Однако они имеют и недостатки и в первую очередь это связано с формированием электронного потока и его прохождением через канал взаимодействия. Если для однолучевых клистронов токопрохождение в динамике составляет 98%, а в статике – 99,9%, то для многолучевых – около 70% - 80% соответственно. Таким образом, остро ощущается необходимость разработки трехмерного программного комплекса, позволившего существенно улучшить характеристики приборов.
Можно выделить и другие факторы, требующие трехмерного приближения, кроме сложной геометрии прибора. Используемые магнитные системы с периодической магнитной фокусировкой (МПФС) из-за наличия отверстий в полюсных наконечниках создают магнитные поля, которые могут существенно отличаться от аксиально-симметричных. Для предотвращения попадания отраженных электронов на катод используется наклон оси пушки по отношению к оси пролетного канала и другие несимметричные элементы.
Кроме того, даже если проектируемое устройство является аксиально-симметричным, то погрешности изготовления и сборки приводят к наличию эллипсности (эксцентриситета), смещению осей отдельных электродов пушки и т.д. Все это приводит к тому, что движение электронов и электромагнитные поля становятся трехмерными.
Прогресс в компьютерных технологиях, увеличивший их вычислительную мощность, разработка численных методов по созданию расчетных сеток и физических моделей сделал возможным создание нового программного комплекса, удовлетворяющего указанным выше требованиям.
В лаборатории Источников мощного микроволнового излучения кафедры радиофизики физического факультета Московского Государственного Университета им. М.В. Ломоносова ведется разработка трехмерного программного комплекса МЛЭП-МГУ [7]. В данной статье представлены основные уравнения и численные методы, на которых основан программный код, а также первые результаты расчета МЛЭП в кинематическом режиме.
1. Основные уравнения и методы расчета.
Задача расчета многолучевой электронной пушки формулируется как решение уравнений Максвелла и уравнений движения системы заряженных частиц (электронов) в электромагнитном статическом поле:
(1)
где– напряженность электрического поля,
– индукция фокусирующего магнитного поля,
- напряженность собственного магнитного поля пучка;
- плотность пространственного заряда,
и
– масса и заряд частиц,
и
– их скорости и импульсы,
– скорость света,
- диэлектрическая проницаемость вакуума,
- плотность тока пучка,
- фактор Лоренца.
Электрическое поле, в общем случае, является суммой полей индуцированных поверхностных зарядов на электродах пушки и собственного поля пучка. Для его нахождения используется теория потенциалов и метод интегральных уравнений, с помощью которого уравнения Максвелла сводятся к интегральному уравнению Пуассона относительно плотности
заряда на поверхности и плотности объемных зарядов:
,
(2)
где
- скалярный потенциал. Благодаря симметрии в структуре пушки можно выделить характерный элемент конструкции, анализом которого можно ограничиться. Соответственно возникают два типа граничных условий: заданные значения потенциалов (U) на проводящих металлических поверхностях – S1 (условия Дирихле) и равенство нулю значений нормальной производной потенциала на плоскостях симметрии – S2 (условие Неймана):
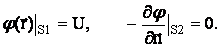
(3)
Для решения интегрального уравнения используются метод конечных поверхностных элементов и метод итераций. На нулевой итерации рассчитывается поле, создаваемое наведенными зарядами на электродах, и объемный заряд пучков электронов, который на следующей итерации подставляется в уравнение Пуассона (2) и происходит перерасчет электрического поля до требуемой сходимости. Также учитывается взаимодействие заряженных частиц между собой и с зарядами на поверхности электродов с помощью закона Кулона. С помощью метода конечных элементов интегральное уравнение (2) сводится к системе линейных алгебраических уравнений (СЛАУ), которая решается на компьютере.
Для траекторного анализа и расчета токов используется метод трубок тока и модифицированный метод Эйлера для решения уравнений движения заряженных частиц. В режиме ограничения тока пространственным зарядом предполагается, что на расстоянии
от эмиттера, достаточно малом по отношению к радиусу кривизны и характерным размерам области, начальное значение плотности тока задается законом Чайлда-Ленгмюра:
(4)
Катод в модели пушки имеет сферическую эмиссионную поверхность, состоящую изэлементов (площадок) величины
. Координаты некоторой серединной точки каждого элемента поверхности катода –
, отстоящей от эмиссионной поверхности на расстояние
по нормали от него, принимаются за начальные координаты для траектории, отождествляемой с элементарной трубкой тока, включающей в себя частицы, вылетающие с данной площадки. Далее проводится интегрирование траекторий от эмитирующей поверхности («виртуального катода») до конца объемной сетки с помощью метода Эйлера и итераций.
Для расчета объемного заряда часть траектории с двумя последовательно рассчитанными координатами электрона делится на N частей. Вклад заряда в определенную ячейку внутри пушки будет вноситься только теми частями, которые попадают в нее. Для расчета полного заряда необходимо просуммировать по всем траекториям, проходящим через ячейку. Рассчитанная плотность объемного заряда на последующей итерации подставляется в уравнение Пуассона (2) и расчет повторяется.
Для расчета магнитного поля в первом приближении используется известное из эксперимента распределение компоненты реверсного магнитного поля на оси пролетного канала, которое интерполируется на весь пролетный канал. Таким образом, магнитное поле имеет параксиальный вид. В дальнейшем планируется по известной структуре магнитной системы рассчитать в трехмерном приближении полное распределение магнитного поля внутри каждого пролетного канала электронной пушки.
Объектом исследования выбрана 18-лучевая электронная пушка широкополосного клистронного усилителя [8]. Катоды располагаются симметрично в два слоя: на внешнем радиусе расположено 12 катодов, на внутреннем – 6 катодов (рис. 1).
Метод конечных элементов хорошо подходит при исследовании сложных структур. Для того чтобы свести интегральное уравнение (2) к СЛАУ необходимо непрерывные величины, например потенциал и поверхностную плотность заряда, аппроксимировать дискретными величинами, определенными на конечном числе подобластей - элементах. С этой целью разработан генератор трехмерной поверхностной сетки, аппроксимирующий электронную пушку треугольными элементами. Теперь непрерывные величины можно аппроксимировать на каждом элементе полиномами, которые определяются с помощью узловых значений этих величин, но при этом непрерывность величин вдоль границ элемента сохраняется.
Благодаря симметрии структуры пушки при анализе можно ограничиться шестой частью исследуемой области (рис. 1), захватывающей три пролетных канала, а полученные результаты можно продолжить на всю область пушки по условиям периодичности (3). Генератор имеет удобный для пользователя графический интерфейс, с помощью которого можно задавать любые параметры пушки и элементов, добиваясь при этом необходимого баланса между точностью решения и временем вычислений. На рис. 2 представлена половина расчетной модели пушки, используемой в расчетах. Можно выделить составляющие ее части: 1 - катоды с внутреннего и внешнего слоя, 2 - фокусирующий электрод, 3 - анод, 4 - трубы дрейфа, 5 - поверхности симметрии. На рис. 3 показана полная расчетная модель 1/6 части МЛЭП, аппроксимированная треугольной поверхностной сеткой.
Используемые методы расчета электромагнитного поля позволяют находить его не во всем внутреннем пространстве модели, а только в области пролета трех электронных пучков, что также экономит вычислительные ресурсы и сокращает время расчета. С этой целью создана равномерная объемная цилиндрическая сетка, заполняющая три пролетных канала в модели, которая начинается у поверхности катода, проходит через отверстие в фокусирующем электроде и заполняет трубу дрейфа.
2. Результаты численного эксперимента.
Определение точности решения трехмерных краевых задач методом интегральных уравнений проводилось на модели, состоящей из одной закрытой трубы дрейфа, которая является составной частью конструкции МЛЭП, и для нее можно построить точное аналитическое решение трехмерной краевой задачи Дирихле для уравнения Лапласа:
(5)
где R0 – радиус трубы дрейфа, Z0 – длина трубы дрейфа, S – боковая поверхность трубы дрейфа.
Потенциал внутри трубы должен быть равен заданному потенциалу на поверхности – 19 кВ. Максимальное отклонение потенциала составило 30 В, таким образом, погрешность расчета составляет 0,16 %.
Для тестирования точности решения уравнения Лапласа с граничными условиями второго рода также использовалась модель трубы дрейфа: на нижней поверхности (S1) задавался потенциал 0 В, на верхней – 19 кВ (S2), а на боковой (S3) – граничные условия второго рода:
(6)
На рис. 4 показано рассчитанное распределение потенциала U внутри данной системы. Проверялось два основных момента: линии уровня должны быть перпендикулярны боковой поверхности и параллельны верхней и нижней поверхности, а также распределение потенциала должно линейно изменяться от нуля до 19 кВ, что следует из аналитического решения системы (6). Оба этих факта подтверждены
численным экспериментом, что говорит о правильности теории расчета уравнения Лапласа с граничными условиями второго рода. Потенциал 9,5 кВ получен точно посередине пространства между верхней и нижней поверхностями.
В расчетах МЛЭП задавались следующие значения потенциалов на электродах: на катодах – 0 В, на фокусирующем электроде - -200 В, на аноде и трубах дрейфа – 19 кВ.
На рис. 5 показано рассчитанное распределение скалярного потенциала на продольном разрезе объемной сетки модели МЛЭП, заполняющей один пролетный канал, так как физическая картина идентична для трех каналов модели. Эквипотенциальные линии отмечены белым цветом. Поведение потенциала внизу объясняется геометрией сферического катода, параллельно которому проходят эквипотенциальные поверхности. Выше происходит провисание потенциала в трубу дрейфа. В трубах дрейфа потенциал остается постоянным. Черным цветом показаны силовые линии со стрелками, указывающими их направленность. Видно, что начинаются они на катоде и фокусирующем электроде и замыкаются на трубу дрейфа и анод. Силовые линии практически перпендикулярны эквипотенциальным.
Область пушки между фокусирующим электродом и анодом (рис. 6) представляет особый интерес для исследования, так как здесь нет аксиально-симметричных элементов, ограничивающих пролетный канал таких, как труба дрейфа или отверстие фокусирующего электрода, поэтому распределение поля не обязательно должно быть аксиально-симметричным.
На рис. 7 представлено распределение скалярного потенциала в поперечном сечении объемной сетки трех пролетных каналов вблизи середины пространства между фокусирующим электродом и анодом. Две верхние области соответствуют внешнему слою поперечных сечений, нижняя – внутреннему слою. Белым цветом показаны линии уровней
скалярного потенциала.
Максимальное значение потенциала для верхних слоев сечений составляет 8 кВ, минимальное – 7,7 кВ; для нижнего слоя максимальное значение потенциала – 8,03 кВ, минимальное – 7,73 кВ. Таким образом, скалярный потенциал для областей с внешнего слоя совпадает в пределах погрешности, но немного меньше, чем с внутреннего слоя. Провисание потенциала в каждом сечении составило 300 В или 4%.
Видно, что в каждой области имеется небольшое двумерное искажение линий уровня скалярного потенциала от аксиальной симметрии. Отличие структуры линий уровня внешнего и внутреннего слоев определяет трехмерное искажение скалярного потенциала. Это может привести к тому, что параметры электронных пучков (первеанс, разброс поперечных скоростей и т.д.) для внешнего и внутреннего слоев могут различаться.
Таблица 1. Параметры электронных пучков.
Слой
Внешний
Внутренний
Ток, А
5,72
5,83
Микропервеанс,
2,18
2,23
В табл. 1 представлены значения токов и микропервеансов для электронных пучков с внутреннего и внешнего слоев, рассчитанные на нулевой итерации в кинематическом режиме без пространственного заряда. Параметры двух электронных пучков с внешнего слоя совпадают в пределах погрешности.
Из таблицы видно, что параметры немного, но отличаются для пучков с разных слоев, что невозможно было бы увидеть с помощью двумерного программного комплекса. Это связано с тем, что значение потенциала в одном поперечном сечении на внутреннем слое немного больше, чем в том же сечении, но на внешнем слое. Фокусирующий электрод сильнее влияет на эмиссию катодов с внешнего слоя и существенно ограничивает ее, вследствие чего уменьшается ток. Назовем это явление «эффектом ограничения катодного тока с внешнего слоя эмиттеров». Он вызван трехмерной геометрией МЛЭП: катоды с внешнего слоя расположены ближе к границе прибора, а с внутреннего – к центру; также по-разному влияют на них отверстия в фокусирующем электроде, труб дрейфа сверху. На внешнем слое расположено в 2 раза больше катодов, поэтому их влияние отлично от влияния катодов с внутреннего слоя. Все вместе дает интегральный эффект на распределение потенциала для внешнего и внутреннего слоя, приводящий к разнице токов в электронных пучках в этих слоях.
Разница в токах пучков может сказаться на группировке электронных потоков. Это приведет к тому, что фаза влета электронных сгустков во входной и выходной резонаторы будут отличны для разных слоев, и КПД многолучевого усилителя уменьшится. Для уменьшения «эффекта ограничения катодного тока с внешнего слоя эмиттеров» необходимо изменить геометрию пушки, например, увеличить радиус отверстия фокусирующего электрода для внешнего слоя.
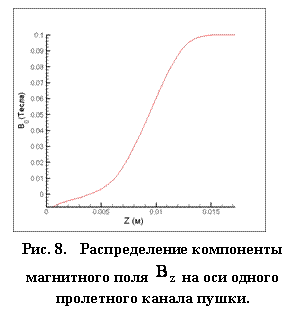
В первом приближении для расчета магнитного поля используется известное из эксперимента распределение компоненты магнитного поля
на оси одного пролетного канала (рис. 8). В отсутствии источников магнитного поля оно описывается уравнением Лапласа, таким образом, распределение магнитного поля внутри всех пролетных каналов электронной пушки получается путем интерполяции известного решения на оси.
Вид рассчитанного параксиального магнитного поля на фоне поверхностной сетки пушки для одного пролетного канала показан на рис. 9., так как структура сетки для всех каналов одинакова, а экспериментальные данные – одни для всех каналов. Данное распределение хорошо согласуется с экспериментальной кривой на рис. 8. На рис. 9 на фоне значений магнитного поля черным цветом показаны силовые линии магнитного поля, которые огибают точку, в которой поле меняет знак, т.е. равно нулю.
Вид траекторий электронов, рассчитанных в кинематическом режиме на нулевой итерации без учета пространственного заряда, представлен на рис. 10. Каждый пучок электронов в модели содержит 456 траекторий. Показаны катоды, с которых стартуют электроны. Так как структура трех электронных пучков в модели
одинакова, то более подробно можно рассмотреть один из них. На рис. 11 представлен вид траекторий одного электронного пучка относительно поверхностной сетки электронной пушки. Видно, что траектории начинают пересекаться внутри трубы дрейфа. Далее пучок начинает вращаться под воздействием магнитного поля, но в данном случае область за кроссовером рассматривать некорректно, так как в расчетах не учитывались силы пространственного заряда пучка. Видно, что пучок сильно сфокусирован и заполняет трубу дрейфа меньше, чем на половину.
3. Заключение.
Приведены результаты численного моделирования многолучевой электронной пушки (МЛЭП) мощного многорезонаторного клистронного усилителя. Даны основные формулы и обсуждаются методы расчета электромагнитных полей для анализа электронно-оптических систем клистронных усилителей в трехмерном приближении. Определена погрешность метода. Представлены первые результаты расчетов многолучевой электронной пушки в кинематическом режиме: распределение электрического поля в пролетных каналах пушки, вид траекторий движения электронных пучков, значения токов и первеансов пучков. Обнаружены трехмерные эффекты, которые невозможно выявить с помощью двумерных программ: не аксиально-симметричный вид структуры силовых линий электрического поля, различие в значениях токов у электронных пучков.
Литература
1. Родякин В.Е., Сандалов А.Н., Программный комплекс Арсенал-МГУ для разработки мощных высокоэффективных клистронных усилителей, Труды VIII Всероссийской школы-семинара “Физика и применение микроволн”, Часть 1, 26-30 мая 2001 г., Звенигород, Московская область, стр. 70-71.
2. Herrmannsfeldt W.B. EGUN An Electron Optics and Gun Design Program. SLAC-331, Stanford University, Stanford, CA. 1988.
3. Ivanov V., Krasnykh A. Analytical computations in solution of 3D problems of physical electronics by BEM2. Proc. IVEC 2003.
4. Королев С.В. Об одной возможности уменьшения веса и размеров клистронов. // Электронная техника. Сер. 1. Электроника СВЧ 1968. в. 9. с. 176-179.
5. Лебединский С.В., Канавец В.И., Васильев Е.И., Гранит Я.Ш., Кучугурный В.И., Сандалов А.Н. Мощные многорезонаторные клистроны (сравнение теории и эксперимента). Электронная техника, сер. I, Электроника СВЧ, 1977, в. 1, с. 41.
6. Сандалов А.Н., Теребилов А.В. Особенности группирования и энергообмена в релятивистском многорезонаторном клистроне. Р и Э, 1983, т. 28, № 9, с. 1803.
7. Kozlov S.V, Pikunov V.M., Sandalov A.N. The Multiple Beam Electron Gun Computer Simulations, Proc. IVEC 2006, p. 91-92.
8. Sandalov A.N., Rodyakin V.E., Chashurina A.N., Ding Yaogen., Shen Bin. Optimization of broadband multiple-beam klystron amplifier. Electromagnetic Waves and Electron Systems 2003, № 11-12, p. 70-75.
Авторы:
Козлов Сергей Владимирович, Пикунов Виктор Михайлович, Сандалов Александр Николаевич
kozlov@phys.msu.ru, pikunov@phys.msu.ru, sandalov@phys.msu.ru
Московский государственный университет им. М.В. Ломоносова, физический факультет
| xxx |