УДК 621.396

RGB – ШКАЛА ДЛЯ ИЗМЕРЕНИЯ РАСПРЕДЕЛЕНИЙ

Ю. Н. Кликушин

Омский государственный технический университет

Получена 25 февраля 2008 г.

 

Описана 3-х компонентная шкала, предназаначенная для измерения формы распределений сигналов. Принцип действия шкалы основан на представлении исследуемого сигнала в виде гистограммы распределения, содержащей всего три моды, подобно тому как это делается при измерении цвета некоторого объекта  с помощью цветовой RGB-шкалы. При изменении формы распределения изменяются весовые коэффициенты мод, которые затем автоматически анализируются встроенной экспертной системой. Результат измерения формируется в виде имени эталонного распределения, расположенного ближе всего к распределению входного сигнала.

 

Кардинальным путем развития теории и технологий измерений является распространение принципа «метризуемости» на все большее число свойств (величин) объектов и процессов окружающего мира. Выраженная словами Галилея - «измеряй неизмеримое» - цель измерений, остается актуальной и в настоящее время.

Характерным примером успешного решения проблемы «измеримости» является трехкомпонентная цветовая шкала, предложенная в конце 20-х годов прошлого века [1]. Любой цвет в этой шкале представляется на особой цветовой плоскости в виде вектора с тремя компонентами (Red-Green-Blue), длина которого определяет яркость, а угловое положение - его цветность. Хотя операции с цветовыми векторами отличаются от аналогичных операций с векторами в обычной векторной алгебре, цветовая шкала позволяет решать главную задачу - аналитически рассчитывать результаты взаимодействия цветовых векторов. Появление цветовой шкалы стимулировало развитие цветного кино и телевидения, а также современных компьютерных систем цветопередачи и цветовоспроизведения.

Похожая ситуация наблюдается в настоящее время с таким свойством, как форма объекта или процесса. Если, например, говорить о сигналах, то их форма является весьма информативной величиной, особенно при решении задач медицинской и технической диагностики. Пока мы не научились измерять форму сигнала (или его характеристик), трудно ожидать прорыва в понимании того, как опытный врач, после визуального просмотра электрокардиограммы пациента, может поставить ему правильный диагноз.

Принципиальная возможность измерения формы распределений сигналов в системе порядковых измерительных шкал была показана в работах [2,3]. Ряд вопросов, связанных с разработкой и исследованием свойств различных инструментов анализа и синтеза формы сигналов и их характеристик, освящен в монографиях [4,5] и публикациях [6-13].

В данной работе описаны принцип действия, устройство и характеристики 3-х компонентной шкалы, предназаначенной для измерения формы распределений сигналов. 

Принцип действия шкалы основан на представлении исследуемого сигнала в виде гистограммы распределения, содержащей всего три моды, подобно тому как это делается при измерении цвета некоторого объекта  с помощью векторной RedGreenBlue-шкалы. При изменении формы распределения изменяются весовые коэффициенты мод, которые затем автоматически анализируются встроенной экспертной системой. Результат измерения формируется в виде имени эталонного распределения, расположенного ближе всего к распределению входного сигнала. В дальнейшем, для краткости, предлагаемый инструмент будем называть RGB-шкалой формы сигналов.

 

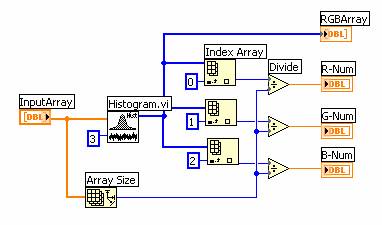
Рис.1. Структура программного кода RGB-шкалы формы сигналов

 

На рис. 1 изображена структура программного кода RGB-шкалы, выполненная в среде графического программирования LabVIEW-7.1. Данный инструмент содержит библиотечные компоненты среды программирования, включающие построитель гистограммы (Histogram.vi), измеритель объема выборки сигнала (Array Size), три фильтра (Index Array), с помощью которых выделяются элементы массива (RGB-Array) по заданным индексам (0; 1 и 2), и три делительных устройства (Divide), на выходе которых формируются весовые коэффициенты (α, β, γ), соответствующие левой (R), средней (G) и правой (B) модам гистограммы (RGB-Array).

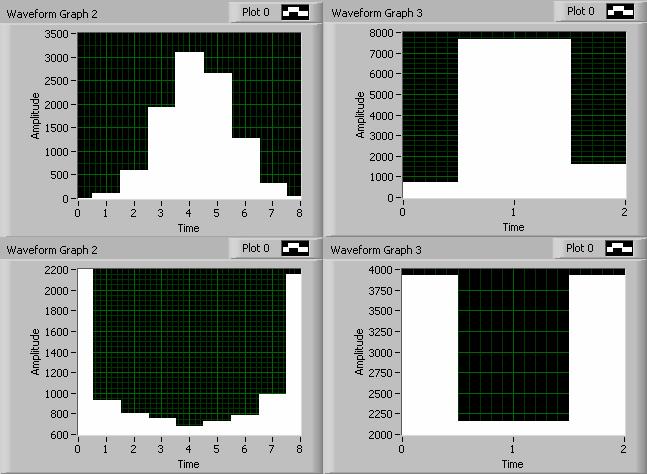
На рис. 2 дан пример, поясняющий принцип работы RGB-шкалы. Левая часть рис. 2 показывает вид распределений входных сигналов с нормальным (вверху) и арксинусным (внизу) распределениями. Правая часть рис. 2 показывает вид гистограм (RGB-Array) этих сигналов, отображенных всего тремя модами. Однако, даже в таком случае, общие особенности (симметрия-асимметрия, выпуклость-вогнутость) исходных распределений – сохраняются.

Если измерять относительную высоту  RGB-мод, можно получить количественную оценку формы распределений в виде весовых коэффициентов векторного уравнения:

.                                                            (1)

 

Рис. 2. Примеры представления распределений входных сигналов (слева) RGB-шкалой (справа)

Уравнение (1), во-первых, по форме аналогично уравнению цветового RGB-вектора [14] и, во-вторых, для него также соблюдается условие нормировки  вида: . Установленная аналогия позволяет ввести два предположения.

1.      Предлагаемый инструмент может быть использован для измерения формы распределений сигналов. Под измерением, в данном случае, понимается присвоение неизвестному анализируемому распределению имени ближайшего эталонного распределения, взятого из некоторого ограниченного их набора. Набор эталонных распределений может представлять, например, реляционную базу данных (БД), записями которой служат имена эталонов, а полями – численные оценки весовых коэффициентов (α, β, γ), полученные в результате предварительной настройки и хранящиеся в памяти экспертной системы. Ограниченное количество эталонов и погрешности задания их весовых коэффициентов указывают на необходимость использования, для получения выходного результата, каких-либо методов интерполяции положения измеряемого распределения относительно реперных точек эталонов.

2.      В рамках RGB-шкалы можно установить алгебру распределений, что позволит аналитически рассчитывать результаты взаимодействия сигналов. По-видимому, операции с векторами в RGB-шкале будут отличаться от подобных же операций в обычной векторной алгебре и, вполне возможно, будут похожи на операции с цветовыми векторами.

Для доказательства первого предположения были проведены эксперименты по измерению распознавательной и частотной идентификационных характеристик RGB-шкалы. Распознавательная ИХ (РИХ) определяет зависимость показаний (в данном случае, весовых коэффициентов α, β, γ) RGB-шкалы от формы входного сигнала. Частотная ИХ (ЧИХ) устанавливает зависимость показаний RGB-шкалы от частоты входного периодического сигнала при постоянстве его формы. В качестве эталонных были выбраны: а) случайные сигналы с симметричными распределениями (2МОД – двумодальным, АРКС – арксинусным, РАВН – равномерным, СИМП – треугольным, НОРМ – нормальным, ЛАПЛ – двусторонним экспоненциальным и КОШИ) и б) периодические сигналы прямоугольной (SQU), синусоидальной (SIN), треугольной (TRI) и пилообразной (SAW)формы.
 

 

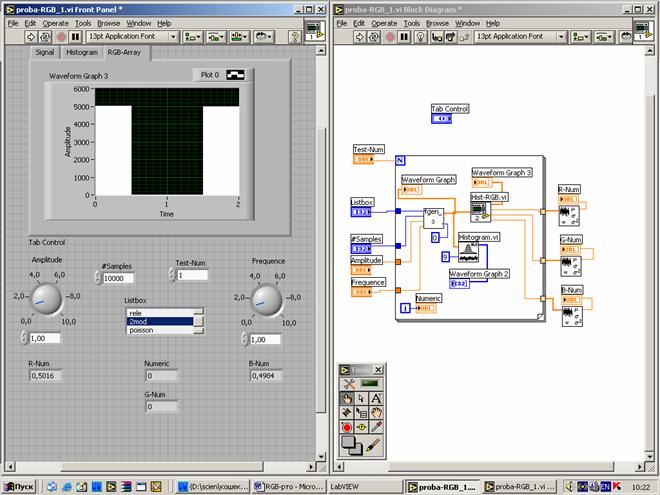
Рис. 3. Передняя панель (слева) и структура программного кода (справа) ВП, предназначенного для исследования  RGB-шкалы

 

Моделирование осуществлялось в структуре виртуального прибора (ВП) Proba-RGB_1.vi (рис.3), который состоял из универсального генератора сигналов (Fgen-3.vi) и RGB-шкалы (рис. 1)  (Hist-RGB.vi). На дисплеи ВП выводились графики сигнала (закладка Signal) генератора и его гистограмма (закладка Histogram), а также гистограмма (RGB-Array)  RGB-шкалы. Результаты измерения весовых коэффициентов (α, β, γ) уравнения (1) индицировались в соответствующих окнах вывода (R-Num, G-Num, B-Num). Для случайных сигналов (кроме КОШИ) проводилось усреднение весовых коэффициентов по количеству (L=100) реализаций объема выборки N=10000. Частота периодических сигналов варьировалась вплоть до граничной (по Котельникову), когда один период содержал только два отсчета.

В табл. 1 и 2 представлены данные измерения РИХ и ЧИХ, соответственно.

Таблица 1.

Распознавательная характеристика RGB-шкалы для эталонных случайных сигналов
 

N=10000, L=100	Имя распределения
	2МОД	АРКС	РАВН	СИМП	НОРМ	ЛАПЛ	КОШИ
R-Num	0,5	0,39	0,333	0,22	0,11	0,05	0
G-Num	0	0,22	0,334	0,56	0,78	0,9	1
B-Num	0,5	0,39	0,333	0,22	0,11	0,05	0

 

Таблица 2.

Частотная характеристика RGB-шкалы для эталонных периодических сигналов
 

SQU	Число периодов сигнала в объеме N=10000
	1	10	100	1000	2000	3000	4000	4999
R-Num	0,5	0,5	0,5	0,5	0,5	0,5	0,5	0,5
G-Num	0	0	0	0	0	0	0	0
B-Num	0,5	0,5	0,5	0,5	0,5	0,5	0,5	0,5
SIN
R-Num	0,39	0,39	0,39	0,39	0,39	0,39	0,39	0,39
G-Num	0,22	0,22	0,22	0,22	0,22	0,22	0,22	0,22
B-Num	0,39	0,39	0,39	0,39	0,39	0,39	0,39	0,39
TRI=SAW
R-Num	0,333	0,333	0,333	0,333	0,333	0,333	0,333	0,333
G-Num	0,334	0,334	0,334	0,334	0,334	0,334	0,334	0,334
B-Num	0,333	0,333	0,333	0,333	0,333	0,333	0,333	0,333

 

Полученные данные позволяют сделать следующие выводы. Во-первых, как и следовало ожидать, показания RGB-шкалы для периодических сигналов от частоты не зависят. Во-вторых, показания RGB-шкалы для треугольного и пилообразного сигналов совпадают TRI=SAW. В-третьих, RGB-шкала не различает классы периодических и случайных сигналов, что объясняется самим принципом действия – измеряется вероятностная функция (гистограмма) сигнала, а не сама временная функция. В-четвертых, у симметричных распределений боковые моды одинаковы R=B. В-пятых, показания RGB-шкалы не зависят от матожидания и дисперсии анализируемого случайного сигнала. Таким образом, можно констатировать, что RGB-шкала обладает свойством масштабной инвариантности и способна измерять форму распределений, включая такие их свойства, как симметрия-асимметрия, выпуклость-вогнутость.

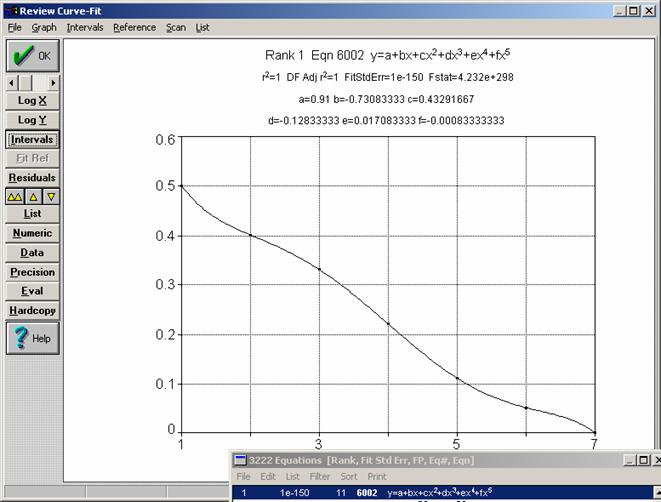
В общем случае РИХ (табл. 1) отображает связь между различными формами распределений, которая может быть выражена аналитически в виде зависимости показаний от порядкового номера распределения (рис. 4 и 5).

Указанные аналитические зависимости получены программой TCWin (фирма Jandel Scientific) в режиме подбора по 4000 моделям собственной БД с использованием критерия минимума среднеквадратического отклонения. Ранг модели (Rank=1) указывает на то, что полученная зависимость является наилучшей.

 

 

Рис. 4. Аналитическая модель РИХ RGB-шкалы для R- и В-мод (по оси Х отложены порядковые номера распределений из табл. 1)

 

 Представленные зависимости можно использовать для решения задачи интерполяции положения неизвестного распределения на RGB-шкале. Для этого, по измеренному значению весового коэффициента путем обратного решения уравнения оценивается порядковый номер, который, в общем случае, может быть рациональным, а не целым, числом.

 Таблица 3.

Распознавательная характеристика RGB-шкалы для тестовых случайных сигналов
 

N=10000, L=100	Имя распределения
	expn	rele	poisson	gamma	binom	bernul
R-Num	0,95	0,67	0,8	0,92	0,25	0,3
G-Num	0,05	0,33	0,2	0,08	0,5	0
B-Num	0	0	0	0	0,25	0,7

В табл. 3 представлены данные тестирования RGB-шкалы 4-мя асимметричными (expn - экспоненциальное, rele - Рэлея, poisson - Пуассона, gamma - гамма, bernul - Бернулли) распределениями и одним – симметричным (binom – биномиальное). Используя зависимость (рис. 4) можно провести интерполяцию положения биномиального распределения с вычислением степени его принадлежности к двум соседним отметкам шкалы: binom ≈[РАВН/0,3; СИМП/0,7]. Другими словами, биномиальное распределение на 70% принадлежит распределению Симпсона и на 30% - равномерному распределению.
 

Рис. 5. Аналитическая модель РИХ RGB-шкалы для G-моды (по оси Х отложены порядковые номера распределений из табл. 1)

 

Перспективы использования RGB-шкалы связаны с построением интеллектуальных систем обработки данных, решающих задачи идентификации и распознавания сигналов.

 

ЛИТЕРАТУРА
 

1.   Пиотровский Я. Теория измерений для инженеров: Пер. с польск.- М.: Мир, 1989.

2.   Кликушин Ю.Н. Нечеткая идентификация формы распределения вероятности. - М.: Измерительная техника, № 9, 1992.

3.  Кликушин Ю.Н. Идентификационные шкалы: теория, технологии, системы // Рук.диссерт. на соиск.ученой степени докт.техн.наук. - Омск: Изд-во ОмГТУ, 2000. - 334 с.

4.    Кликушин Ю.Н. Технологии идентификационных шкал в задаче распознавания сигналов // Монография. - Омск: Изд-во ОмГТУ, 2006 - 96 с.

5. Кликушин Ю.Н., Кошеков К.Т. Методы и средства идентификационных измерений сигналов. Монография.  – Петропавловск: Изд-во СКГУ им. М.Козыбаева, 2007. – 186 с.

6.   Кликушин Ю.Н. Представление случайных сигналов с помощью принадлежностных спектров // Интернет-статья. - М.: Журнал Радиоэлектроники, Изд-во ИРЭ РАН, № 2 (февраль), 2000 г. - http://jre.cplire.ru

7. Кликушин Ю.Н. Фрактальная шкала для измерения распределений вероятности // Интернет-статья. - М.: Журнал Радиоэлектроники, Изд-во ИРЭ РАН, № 3 (март), 2000 г. - http://jre.cplire.ru

8. Кликушин Ю.Н. Классификатор сигналов // Интернет-статья. - М.: Журнал Радиоэлектроники, Изд-во ИРЭ РАН, № 10 (октябрь), 2007 г. - http;//jre.cplire.ru

9. Кликушин Ю.Н. Количественная оценка свойств "регулярности-хаотичности" сигналов // Интернет-статья. - М.: Журнал Радиоэлектроники, Изд-во ИРЭ РАН, № 10 (октябрь), 2006 г. - http://jre.cplire.ru

10. Кликушин Ю.Н., Кобенко В.Ю. Основы идентификационных измерений // Интернет-статья. - М.: Журнал Радиоэлектроники, Изд-во ИРЭ РАН, № 11 (октябрь), 2006 г. - http://jre.cplire.ru

11. Кликушин Ю.Н. Технологии идентификационных шкал //Материалы 7-ой Международной конференции «Актуальные проблемы электронного приборостроения- АПЭП-2004». - Новосибирск: Изд-во НГТУ, т.З, с.52-57, 2004.

12. Кликушин Ю.Н., Кошеков К.Т. Принципы построения средств идентификационных измерений сигналов. – Омский Научный Вестник. Серия: Приборы, машины и технологии. – Изд-во ОмГТУ, № 1(52), 2007.- с.85-89.

13.Кликушин Ю.Н., Кошеков К.Т. Идентификационная шкала, разделяющая случайные и периодические сигналы // Вестник Восточно-Казахстанского государственного технического университета им. Д. Серикбаева. –  2005. – № 4 (30). – С. 34 - 39.

14.  Кривошеев М.И., Кустарев А.К. Цветовые измерения. – М.: Энергоатомиздат, 1990. – 240 с.