УДК 621.396.67
ВЗАИМОДЕЙСТВИЕ ПРЯМЫХ ВОЛН В НЕЛИНЕЙНОМ ЭЛЕКТРОМАГНИТНОМ КРИСТАЛЛЕ
С. Е. Банков
Институт радиотехники и электроники им. В.А.Котельникова РАН
Получена 1 марта 2011 г.
Аннотация. Рассмотрено взаимодействие электромагнитных волн, распространяющихся на первой и второй гармониках основной частоты, в двумерном электромагнитном кристалле с нелинейными емкостями. Исследуется режим пространственного синхронизма прямых волн на основной частоте и на второй гармонике. Определены два способа достижения пространственного синхронизма в электромагнитном кристалле: взаимодействие волн одного типа при условии компенсация емкости и взаимодействие волн разных типов. Построена приближенная модель в виде системы нелинейных дифференциальных уравнений. Исследуются ее различные частные решения. Приводятся результаты численных экспериментов.
Ключевые слова: электромагнитный кристалл, нелинейные волны, пространственный синхронизм.
Abstarct. Interaction of electromagnetic waves propagating at the first and second harmonics of a dominant frequency inside two-dimensional non-linear electromagnetic crystal with non-linear capacitors is considered. Regime of a spatial synchronism of two waves at the first and second harmonics is studied. Conditions of spatial synchronism realization in electromagnetic crystal are investigated. An approximate model of electromagnetic crystal in form of a system of non-linear differential equations is proposed. Several selected solutions of the system are analytically studied. Results of numerical experiments are presented.
Keywords: electromagnetic crystal, non-linear waves, spatial synchronism.
Постановка задачи
Данная работа посвящена
исследованию взаимодействия электромагнитных волн в нелинейных периодических
структурах СВЧ диапазона, получивших название электромагнитных кристаллов
(ЭМК). Известно несколько видов таких взаимодействий [1]. Особый интерес
представляют явления, происходящие в условиях пространственного синхронизма
волн ЭМК, распространяющихся на разных гармониках основной частоты ![]() . Мы рассматриваем
установившиеся периодические процессы, в которых зависимость всех электрических
параметров от времени может быть описана суммой гармоник вида
. Мы рассматриваем
установившиеся периодические процессы, в которых зависимость всех электрических
параметров от времени может быть описана суммой гармоник вида ![]() . Здесь
. Здесь ![]() - круговая частота,
- круговая частота, ![]() - номер гармоники, который принимает
положительные и отрицательные значения. Основная частота
- номер гармоники, который принимает
положительные и отрицательные значения. Основная частота ![]() задается источником,
возбуждающим ЭМК при этом возможно также наличие источника на удвоенной частоте
задается источником,
возбуждающим ЭМК при этом возможно также наличие источника на удвоенной частоте
![]() .
.
Следует отметить, что типичной для ЭМК, а также для фотонных кристаллов ситуацией является слабая нелинейность отдельного элемента. Поэтому сильные эффекты в таких структурах могут возникать только как результат когерентного сложения множества слабых нелинейных взаимодействий. Указанное выше когерентное сложение возникает при выполнении условий пространственного синхронизма.
В теории волн в нелинейных средах известен пространственный синхронизм сонаправленных волн [2]. Он возникает при выполнении следующего условия:
![]() , (1)
, (1)
где ![]() - целые числа, имеющие смысл номеров
гармоник основной частоты
- целые числа, имеющие смысл номеров
гармоник основной частоты ![]() ,
, ![]() - коэффициент замедления волны в среде,
- коэффициент замедления волны в среде, ![]() - ее постоянная
распространения,
- ее постоянная
распространения, ![]() -
волновое число свободного пространства.
-
волновое число свободного пространства.
Термин сонаправленные волны
показывает, что речь идет о волнах, имеющих вектора Пойнтинга и волновые
вектора, ориентированные в одном направлении. Синхронизм сонаправленных волн
приводит к интенсивной связи волн на частотах ![]() и
и ![]() , которая может приводить, например, к
полной перекачке энергии с основной частоты на кратную ей частоту.
, которая может приводить, например, к
полной перекачке энергии с основной частоты на кратную ей частоту.
Особенностью периодических структур является возможность распространения в них обратных волн [3], у которых вектор Пойнтинга и волновой вектор направлены в противоположные стороны. Существование обратных волн порождает новый вид пространственного синхронизма, который не возникает в непрерывных средах: синхронизм противонаправленных волн [4]. Под противонаправленными волнами мы понимает волны, у которых вектора Пойнтинга сонаправлены, а волновые вектора противонаправлены. Очевидно, что в этом случае одна из волн является прямой, а другая обратной. Условие синхронизма имеет следующий вид:
Отметим, что синхронизм противонаправленных волн является эффектом характерным исключительно для ЭМК. Возможность аномального поведения электромагнитных волн при выполнении условия (2) отмечалась в работе [4].
Целью данной работы является изучение синхронизма сонаправленных волн в ЭМК. Отметим, что, как показали результаты исследований, качественно оно во многом аналогично поведению волн в непрерывных нелинейных средах. Поэтому основное внимание мы уделим следующим вопросам: реализация режима пространственного синхронизма в ЭМК, аналитическое исследование распространения волн в ЭМК, численное исследование характеристик ЭМК в режиме пространственного синхронизма.
1. Математическая модель ЭМК
Исследуемая структура показана на рис. 1. Она
представляет собой два металлических экрана, образующих плоский волновод (ПВ).
Внутри ПВ расположена решетка металлических цилиндров радиуса ![]() . В общем случае она
имеет бесконечные размеры по оси 0у и конечные размеры по оси 0х. Размеры
решетки по этой оси задаются числом
. В общем случае она
имеет бесконечные размеры по оси 0у и конечные размеры по оси 0х. Размеры
решетки по этой оси задаются числом ![]() . В цилиндры включены сосредоточенные
нелинейные емкости. Решетка, формирующая ЭМК, возбуждается плоской волной,
падающей под углом падения
. В цилиндры включены сосредоточенные
нелинейные емкости. Решетка, формирующая ЭМК, возбуждается плоской волной,
падающей под углом падения ![]() на основной частоте
на основной частоте ![]() .
.
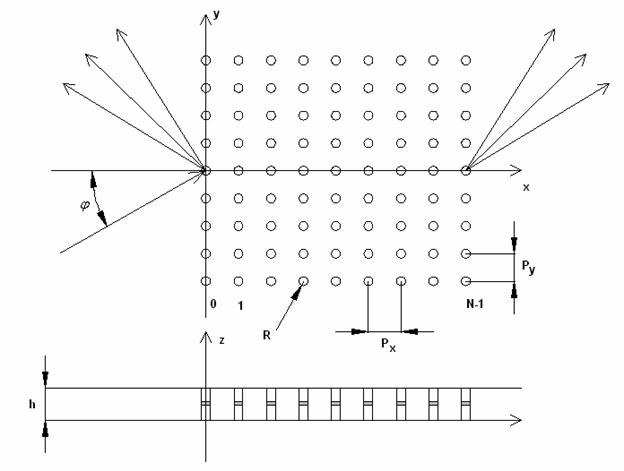
Рис. 1. Исследуемая структура.
Модель представленной выше структуры получена в работе [5]. Поэтому мы не будем подробно рассматривать вывод уравнений, к которым сводится граничная задача для электромагнитного поля, а приведем основные соотношения без вывода:
![]() ,
,
![]() ,
,
где
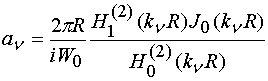 , (4)
, (4)
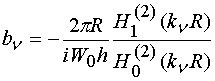 ,
,
![]() ,
,
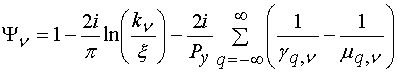 ,
,
![]() ,
, ![]() ,
,
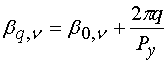 ,
,
![]() ,
, ![]() ,
,
где ![]() - символ Кронекера,
- символ Кронекера, ![]() - волновое сопротивление среды
внутри ПВ,
- волновое сопротивление среды
внутри ПВ, ![]() -
волновое число свободного пространства на частоте
-
волновое число свободного пространства на частоте ![]() ,
, ![]() - высота ПВ,
- высота ПВ, ![]() - периоды решетки ЭМК,
- периоды решетки ЭМК, ![]() - номер максимальной гармоники
основной частоты, учитываемой в решении,
- номер максимальной гармоники
основной частоты, учитываемой в решении, ![]() - номер гармоники основной частоты.
Индексы
- номер гармоники основной частоты.
Индексы ![]() описывают
положение элемента ЭМК по оси 0х. Вектора
описывают
положение элемента ЭМК по оси 0х. Вектора ![]() и
и ![]() имеют размерность равную
имеют размерность равную ![]() . Их элементами
соответственно являются токи, текущие по цилиндрам ЭМК и напряжения на
нелинейных емкостях. Вектор
. Их элементами
соответственно являются токи, текущие по цилиндрам ЭМК и напряжения на
нелинейных емкостях. Вектор ![]() имеет такую же размерность, а его
элементами являются напряженности компоненты поля
имеет такую же размерность, а его
элементами являются напряженности компоненты поля ![]() падающей волны в центрах цилиндров ЭМК.
При выводе соотношений (2) – (5) принято во внимание, что в силу периодичности
ЭМК по оси 0у все электродинамические параметры имеют экспоненциальную
зависимость от индекса
падающей волны в центрах цилиндров ЭМК.
При выводе соотношений (2) – (5) принято во внимание, что в силу периодичности
ЭМК по оси 0у все электродинамические параметры имеют экспоненциальную
зависимость от индекса ![]() :
:
![]() .
.
Индекс ![]() описывает положение центра
элемента ЭМК по оси 0у. Волновое число
описывает положение центра
элемента ЭМК по оси 0у. Волновое число ![]() задается падающей волной, поле которой
описывается следующим образом:
задается падающей волной, поле которой
описывается следующим образом:
![]() , (6)
, (6)
![]() .
.
В уравнении (3) под ![]() понимается нелинейный оператор, связывающий гармоники
тока с гармониками напряжения на нелинейных емкостях. В общем случае он имеет
следующий вид:
понимается нелинейный оператор, связывающий гармоники
тока с гармониками напряжения на нелинейных емкостях. В общем случае он имеет
следующий вид:
 , (7)
, (7)
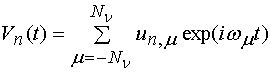 .
.
В формуле (7) индекс ![]() - это номер элемента
ЭМК, задающий его положение на оси 0х,
- это номер элемента
ЭМК, задающий его положение на оси 0х, ![]() - нелинейная емкость, зависящая от
напряжения
- нелинейная емкость, зависящая от
напряжения ![]() .
.
Благодаря оператору ![]() система уравнений (5) становится
нелинейной системой, которую в общем случае можно решить только численными
методами.
система уравнений (5) становится
нелинейной системой, которую в общем случае можно решить только численными
методами.
2. Условия реализации пространственного синхронизма волн
В данном разделе мы рассмотрим условия, при которых в ЭМК возникает пространственный синхронизм сонаправленных волн. Сложность его реализации заключается в необходимости одновременного удовлетворения условию кратности частот и условию равенства коэффициентов замедления волн. Изучение собственных волн линейного ЭМК показывает, что они могут иметь одинаковые коэффициенты замедления на разных частотах, однако при этом отношение частот совсем не обязательно равно двум или, по крайней мере, является натуральным числом.
Отметим, что постоянные
распространения собственных волн ЭМК ![]() получаются из решения следующего
уравнения:
получаются из решения следующего
уравнения:
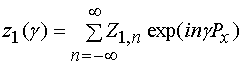 ,
,
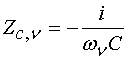 ,
,
где ![]() - линейная емкость. Индексы в уравнении
(8) означают, что данные величины берутся на основной частоте
- линейная емкость. Индексы в уравнении
(8) означают, что данные величины берутся на основной частоте ![]() . В принципе для
линейной системы индекс
. В принципе для
линейной системы индекс ![]() не имеет смысла, так как в ней поля на
кратных частотах не возникают. Мы его сохранили для единообразия обозначений
введенных в формулах (3) – (5).
не имеет смысла, так как в ней поля на
кратных частотах не возникают. Мы его сохранили для единообразия обозначений
введенных в формулах (3) – (5).
Изучение собственных волн линейного ЭМК
необходимо для определения условий возникновения пространственного синхронизма.
Ограничимся исследованием волн на частотах ![]() и
и ![]() . Рассмотрим два случая. Отметим, что ЭМК
является более сложным объектом, чем однородная среда. Поэтому в нем возможен
режим многоволнового распространения. В этом режиме в ЭМК существуют две и
более волны, отличающиеся друг от друга структурой поля и постоянными
распространения. Также в ЭМК можно создать условия, при которых на частотах
. Рассмотрим два случая. Отметим, что ЭМК
является более сложным объектом, чем однородная среда. Поэтому в нем возможен
режим многоволнового распространения. В этом режиме в ЭМК существуют две и
более волны, отличающиеся друг от друга структурой поля и постоянными
распространения. Также в ЭМК можно создать условия, при которых на частотах ![]() и
и ![]() существует один
распространяющийся тип волны. Такой режим принято называть одноволновым.
Возникновение многоволнового режима в ЭМК существенно зависит от его периодов
существует один
распространяющийся тип волны. Такой режим принято называть одноволновым.
Возникновение многоволнового режима в ЭМК существенно зависит от его периодов ![]() и от угла
распространения волны
и от угла
распространения волны ![]() ,
то есть угла между волновым вектором волны
,
то есть угла между волновым вектором волны ![]() и осью 0х. Таким образом, мы предполагаем,
что в общем случае волна может распространяться в плоскости XOY
под произвольным углом к осям координат (см. рис. 2).
и осью 0х. Таким образом, мы предполагаем,
что в общем случае волна может распространяться в плоскости XOY
под произвольным углом к осям координат (см. рис. 2).
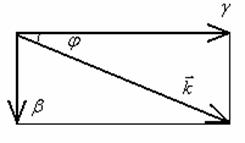
Рис. 2. К определению направления распространения волны.
Из рис. 2 видно, что постоянная распространения ![]() является проекцией
волнового вектора на ось 0х. Его проекцию на ось 0у -
является проекцией
волнового вектора на ось 0х. Его проекцию на ось 0у - ![]() считаем фиксированной величиной,
а из уравнения (8) находим значение
считаем фиксированной величиной,
а из уравнения (8) находим значение ![]() . Непосредственно задавать величину
. Непосредственно задавать величину ![]() неудобно. Для ее
определения введем угол падения
неудобно. Для ее
определения введем угол падения ![]() :
:
Угол распространения ![]() определяется через угол падения из
уравнения:
определяется через угол падения из
уравнения:
![]() . (10)
. (10)
Угол падения имеет простой смысл, который состоит
в том, что он равен углу, под которым на ЭМК падает Т – волна ПВ, имеющая
проекцию волнового вектора на ось 0у равную ![]() . Такая волна возбуждает в ЭМК его
собственные волны, имеющие такую же проекцию на волнового вектора на ось 0у.
Таким образом, с помощью угла падения
. Такая волна возбуждает в ЭМК его
собственные волны, имеющие такую же проекцию на волнового вектора на ось 0у.
Таким образом, с помощью угла падения ![]() мы можем одинаково описывать, как
распространение собственных волн в бесконечном ЭМК, так и возбуждение ЭМК
внешним полем.
мы можем одинаково описывать, как
распространение собственных волн в бесконечном ЭМК, так и возбуждение ЭМК
внешним полем.
Рассмотрим два способа создания
режима пространственного синхронизма сонаправленных волн. Первый из них можно
назвать методом компенсации емкости. Он реализуется при параллельном
подключении к нелинейной емкости ![]() дополнительной цепи, состоящей из
сосредоточенных реактивных элементов (см. рис. 3).
дополнительной цепи, состоящей из
сосредоточенных реактивных элементов (см. рис. 3).
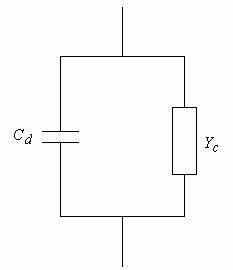
Рис. 3. Нелинейная емкость с дополнительной цепью.
Проводимость цепи обозначим
через ![]() и
потребуем выполнения следующих условий:
и
потребуем выполнения следующих условий:
![]() ,
,
где ![]() - линейная часть емкости
- линейная часть емкости ![]() (
(![]() ),
), ![]() - частота пространственного синхронизма
для первой гармоники.
- частота пространственного синхронизма
для первой гармоники.
Из системы уравнений (11) видно, что при ее
выполнении суммарная проводимость, включенная в металлический цилиндр,
являющийся элементом ЭМК, равна нулю. В этом случае ток через цилиндр не течет,
что эквивалентно его отсутствию в составе ЭМК. Если внутри ПВ нет цилиндров,
или, по крайней мере, отсутствует их влияние на электромагнитное поле, то это
означает, что внутри ПВ распространяются его собственные волны. Наибольший
интерес представляет основная Т – волна, имеющая на любой частоте коэффициент
замедления равный единице. Таким образом, мы приходим к выводу о том, что на
частотах ![]() и 2
и 2![]() в ЭМК распространяются
волны с одинаковыми коэффициентами замедления, что говорит о существовании в
ЭМК искомого режима пространственного синхронизма.
в ЭМК распространяются
волны с одинаковыми коэффициентами замедления, что говорит о существовании в
ЭМК искомого режима пространственного синхронизма.
Структура дополнительной цепи может быть достаточна произвольной. Остановимся на цепи лестничного типа известной в теории фильтров [6]. Простейшая цепь, с помощью которой можно удовлетворить системе уравнений (11), содержит три элемента. Два варианта выполнения такой цепи показаны на рис. 4.
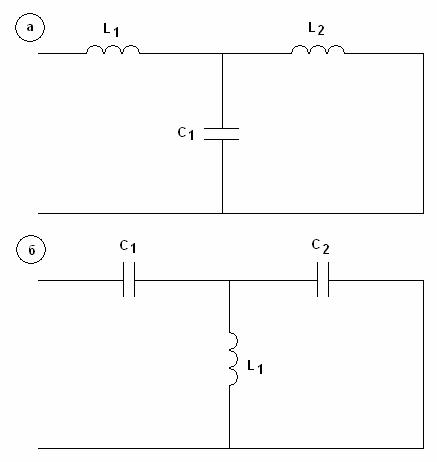
Рис. 4. Принципиальные схемы дополнительной цепи.
Поскольку для выполнения системы уравнений (11)
необходимо, чтобы импеданс дополнительной цепи на частотах ![]() и 2
и 2![]() имел индуктивный характер, то более
естественным представляется использование схемы, показанной на рис. 4 а. Ее
проводимость может быть выражена следующим образом:
имел индуктивный характер, то более
естественным представляется использование схемы, показанной на рис. 4 а. Ее
проводимость может быть выражена следующим образом:
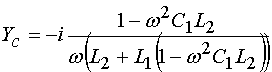 . (12)
. (12)
Подставляя формулу (12) в систему (11), получим
систему уравнений для определения неизвестных ![]() и
и ![]() . Видно, что число уравнений недостаточно
для однозначного решения поставленной задачи. Поэтому мы имеем возможность
фиксировать один из искомых параметров или сформулировать дополнительное
условие. Например, мы можем потребовать, чтобы суммарная проводимость,
включенная в цилиндр, стремилась к бесконечности на некоторой частоте
. Видно, что число уравнений недостаточно
для однозначного решения поставленной задачи. Поэтому мы имеем возможность
фиксировать один из искомых параметров или сформулировать дополнительное
условие. Например, мы можем потребовать, чтобы суммарная проводимость,
включенная в цилиндр, стремилась к бесконечности на некоторой частоте ![]() удовлетворяющей
неравенству:
удовлетворяющей
неравенству:
![]() . (13)
. (13)
От способа формулировки
дополнительного условия поведение собственных волн меняется весьма
незначительно. От него преимущественно зависят номиналы реактивных элементов
дополнительной цепи ![]() и
и
![]() .
.
Рассмотрим численный пример,
показывающий возможность реализации пространственного синхронизма с помощью
метода скомпенсированной емкости. ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Размеры здесь и далее даны в миллиметрах,
емкости в пикофарадах и индуктивности в наногенри. В качестве дополнительного
условия взято равенство полной проводимости бесконечности на частоте
. Размеры здесь и далее даны в миллиметрах,
емкости в пикофарадах и индуктивности в наногенри. В качестве дополнительного
условия взято равенство полной проводимости бесконечности на частоте ![]() =7 ГГц (
=7 ГГц (![]() ). Частота
). Частота ![]() взята равной 4.5 ГГц.
взята равной 4.5 ГГц.
На рис. 5 показана частотная зависимость коэффициента замедления волны ЭМК. Важно, что кривые на рис. 5 соответствуют одной волне ЭМК основного типа. Таким образом, мы можем сделать вывод о том, что рассматриваемый ЭМК находится в одноволновом режиме.
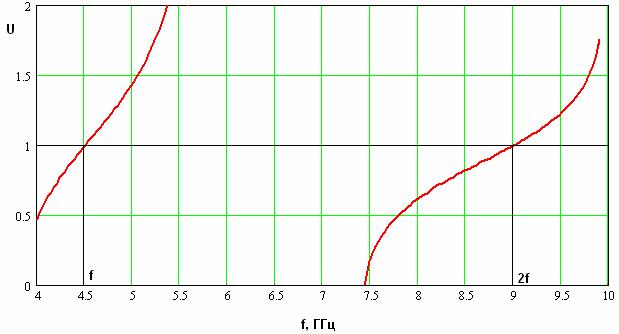
Рис. 5. Частотная зависимость коэффициента замедления основной волны ЭМК.
Возможность реализации пространственного синхронизма собственных волн ЭМК в одноволновом режиме является существенным преимуществом метода скомпенсированной емкости.
Из рис. 5 также видно, что на частотах 4.5 и 9 ГГц волна ЭМК имеет одинаковый коэффициент замедления равный единице.
Интересные выводы позволяет сделать анализ двух
графиков функций ![]() и
и
![]() , если их
построить в окрестности значения аргумента равного 4.5. Такие графики
представлены на рис. 6. Кривая 1 соответствует функции
, если их
построить в окрестности значения аргумента равного 4.5. Такие графики
представлены на рис. 6. Кривая 1 соответствует функции ![]() , а кривая 2 функции
, а кривая 2 функции ![]() .Видно, что два графика
не пересекаются в одной точке, как этого можно было ожидать, а касаются друг
друга. В результате коэффициенты замедления на кратных частотах оказываются
близкими друг другу в некотором диапазоне частот. Поэтому условия близкие к условиям
пространственного синхронизма выполняются в полосе частот, хотя исходили мы
(см. систему (11)) из требований сформулированных только для частоты
.Видно, что два графика
не пересекаются в одной точке, как этого можно было ожидать, а касаются друг
друга. В результате коэффициенты замедления на кратных частотах оказываются
близкими друг другу в некотором диапазоне частот. Поэтому условия близкие к условиям
пространственного синхронизма выполняются в полосе частот, хотя исходили мы
(см. систему (11)) из требований сформулированных только для частоты ![]() .
.
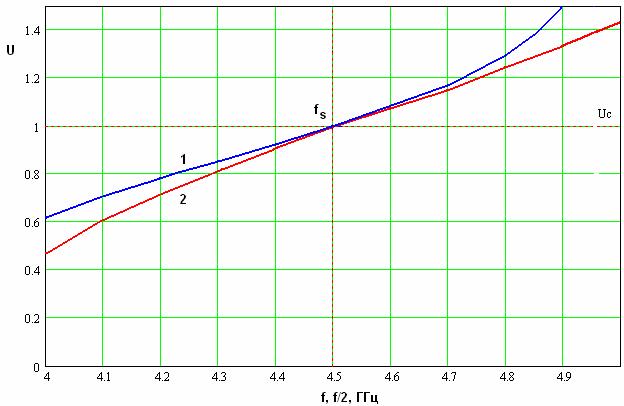
Рис. 6. Частотная зависимость коэффициента замедления.
Другой способ реализации пространственного
синхронизма заключается в использовании многоволнового режима в ЭМК на частоте ![]() . При этом
дополнительная цепь к емкости не подключается, но рассматривается
распространение волн в ЭМК под некоторым углом к оси 0х.
. При этом
дополнительная цепь к емкости не подключается, но рассматривается
распространение волн в ЭМК под некоторым углом к оси 0х.
Необходимость использования ненулевых углов
падения ![]() обусловлена
тем, что условия синхронизма даже в многоволновом ЭМК, но при
обусловлена
тем, что условия синхронизма даже в многоволновом ЭМК, но при ![]() =0 выполнить не удалось.
Для пояснения причин этой ситуации рассмотрим частотную зависимость модуля
коэффициента замедления собственных волн ЭМК. Параметры ЭМК выбраны таким
образом, чтобы в некотором диапазоне частот в нем могли распространяться две и
более волны.
=0 выполнить не удалось.
Для пояснения причин этой ситуации рассмотрим частотную зависимость модуля
коэффициента замедления собственных волн ЭМК. Параметры ЭМК выбраны таким
образом, чтобы в некотором диапазоне частот в нем могли распространяться две и
более волны.
Указанная зависимость представлена на рис. 7. Она
получена при ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Красным цветом показан коэффициент
замедления основной волны ЭМК, а синий соответствует первому высшему типу. Из
рис. 7 хорошо видна зонная структура ЭМК. Рассмотрим ее подробнее.
. Красным цветом показан коэффициент
замедления основной волны ЭМК, а синий соответствует первому высшему типу. Из
рис. 7 хорошо видна зонная структура ЭМК. Рассмотрим ее подробнее.
На низких частотах мы имеем полосу пропускания.
Присвоим ей нулевой номер. В этой полосе пропускания основная волна ЭМК имеет
замедленный характер (![]() ).
При повышении частоты распространяющиеся волны в ЭМК исчезают и он попадает в
полосу запирания с нулевым номером. В диапазоне частот 6.2-15 ГГц наблюдается
первая полоса пропускания (
).
При повышении частоты распространяющиеся волны в ЭМК исчезают и он попадает в
полосу запирания с нулевым номером. В диапазоне частот 6.2-15 ГГц наблюдается
первая полоса пропускания (![]() ), в которой сохраняется одноволновый режим
распространения. Первую полосу пропускания сменяет довольно узкая первая полоса
запирания, которую также называют Брэгговской.
), в которой сохраняется одноволновый режим
распространения. Первую полосу пропускания сменяет довольно узкая первая полоса
запирания, которую также называют Брэгговской.
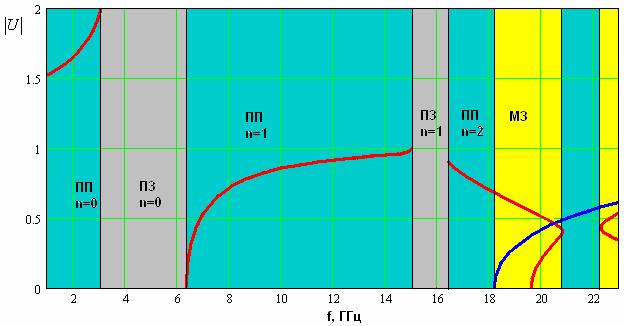
Рис. 7. Частотная зависимость модуля
коэффициента замедления при ![]() .
.
Начиная с некоторой частоты, которая в
рассматриваемом случае равна 18.1 ГГц, в ЭМК распространяются две волны разных
типов. При этом одна из них – основная является обратной волной, а волна
высшего типа прямой. Назовем полосу пропускания с несколькими распространяющимися
волнами многоволновой зоной. Будем оптимизировать параметры ЭМК с целью
получить равные коэффициенты замедления основной волны в первой полосе
пропускания и волны высшего типа в многоволновой зоне. К сожалению, выполнить
условия пространственного синхронизма для этих волн при ![]() не удается.
не удается.
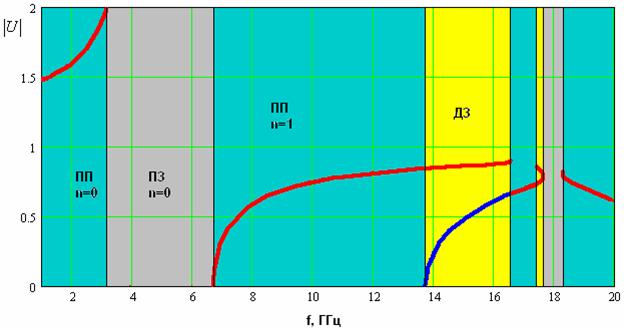
Рис. 8. Частотная
зависимость модуля коэффициента замедления при ![]()
Увеличения угла падения резко сдвигает вниз по
частоте точку возникновения многоволновой зоны, при этом слабо влияя на
основную волну. В этом можно убедиться, анализируя графики на рис. 8, на
котором показана частотная зависимость модуля коэффициента замедления при ![]() . Благодаря указанному
изменению поведения кривых возникает возможность обеспечить равенство
коэффициентов замедлений основной и высшей волн на кратных частотах
. Благодаря указанному
изменению поведения кривых возникает возможность обеспечить равенство
коэффициентов замедлений основной и высшей волн на кратных частотах ![]() и 2
и 2![]() .
.
О выполнении условий пространственного
синхронизма для двух рассматриваемых волн говорят графики на рис. 9. На рис. 9
показаны графики уже использованных функций ![]() и
и ![]() , которым соответствуют кривые 1 и 2.
, которым соответствуют кривые 1 и 2.
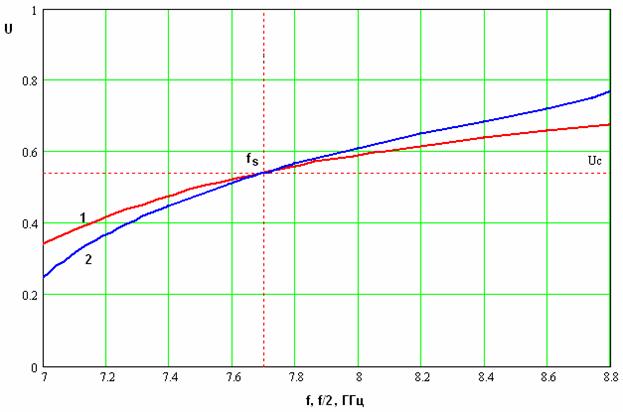
Рис. 9. Частотная зависимость коэффициента замедления.
Из рис. 9 видно, что кривые имеют единственную
точку пересечения при ![]() =7.7
ГГц. В точке пересечения коэффициент замедления равен
=7.7
ГГц. В точке пересечения коэффициент замедления равен ![]() =0.55. Отметим, принципиальную
разницу между двумя рассмотренными способами реализации режима пространственного
синхронизма. Метод скомпенсированной емкости работает в одноволновом режиме, а
метод, использующий волны высших типов принципиально реализуем только в
многоволновом режиме, в котором кроме двух волн, находящихся в синхронизме
существуют также другие волны, которые могут отбирать энергию у
взаимодействующих волн и благодаря этому существенно влиять на их
распространение.
=0.55. Отметим, принципиальную
разницу между двумя рассмотренными способами реализации режима пространственного
синхронизма. Метод скомпенсированной емкости работает в одноволновом режиме, а
метод, использующий волны высших типов принципиально реализуем только в
многоволновом режиме, в котором кроме двух волн, находящихся в синхронизме
существуют также другие волны, которые могут отбирать энергию у
взаимодействующих волн и благодаря этому существенно влиять на их
распространение.
3. Модель ЭМК в режиме синхронизма сонаправленных волн
Непосредственное использование
модели ЭМК в виде уравнений (3) – (5) для анализа ЭМК в режиме синхронизма
оказывается неэффективным. Проблема состоит в том, что взаимодействие волн ЭМК
происходит в виде периодического или квазипериодического процесса, который
формируется на расстояниях многократно превышающих период ЭМК. Таким образом,
для его исследования необходимо анализировать электромагнитное поле в структуре
с весьма большим числом элементов вдоль оси 0х ![]() . Прямое численное решение нелинейной
системы (3) в этом случае часто сопровождается неустойчивостью и может вообще
быть расходящимся. Поэтому возникает необходимость адаптации модели к условиям
синхронизма.
. Прямое численное решение нелинейной
системы (3) в этом случае часто сопровождается неустойчивостью и может вообще
быть расходящимся. Поэтому возникает необходимость адаптации модели к условиям
синхронизма.
Уравнения (3) – (5) могут использоваться для нелинейных элементов с разной зависимостью емкости от напряжения на ней. Также в них отсутствуют ограничения на количество учитываемых гармоник. Модель, которая будет построена в данном разделе имеет ограниченную область использования. Она учитывает только взаимодействие первой и второй частотных гармоник. Кроме того, она справедлива для емкостей с простейшей линейной зависимостью от напряжения:
![]() , (14)
, (14)
которая, вообще говоря, верна только при достаточно малых напряжениях на емкости.
При построении модели будем использовать уже
отмеченное свойство процессов в ЭМК, а именно медленное изменение напряжений на
емкостях на периоде ЭМК ![]() . Кроме того, будем рассматривать ЭМК
находящиеся в одноволновом режиме на частотах
. Кроме того, будем рассматривать ЭМК
находящиеся в одноволновом режиме на частотах ![]() и
и ![]() . Из этого условия следует, что пространственный
синхронизм реализован по методу скомпенсированной емкости (см. раздел 2).
. Из этого условия следует, что пространственный
синхронизм реализован по методу скомпенсированной емкости (см. раздел 2).
Сформулированные Выше приближения позволяют перейти от исходной системы уравнений (3) к более простой системе:
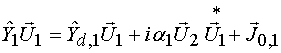 , (15)
, (15)
![]() ,
,
где ![]() ,
, ![]() - диагональные матрицы, у которых на
главной диагонали стоят проводимости элементов, включенных в цилиндры ЭМК.
Нетрудно увидеть, что эти проводимости равны проводимости линейной емкости плюс
проводимость компенсирующей цепи. На частоте пространственного синхронизма
суммарная проводимость равна нулю на частотах первой и второй гармоник. Символ * означает операцию комплексного сопряжения.
- диагональные матрицы, у которых на
главной диагонали стоят проводимости элементов, включенных в цилиндры ЭМК.
Нетрудно увидеть, что эти проводимости равны проводимости линейной емкости плюс
проводимость компенсирующей цепи. На частоте пространственного синхронизма
суммарная проводимость равна нулю на частотах первой и второй гармоник. Символ * означает операцию комплексного сопряжения.
Операции
над векторами в формулах (9) применяются почленно к элементам векторов с
одинаковыми индексами. Таким образом, например, ![]() - это вектор со следующими элементами:
- это вектор со следующими элементами:
![]() . (16)
. (16)
В развернутой форме система уравнений (15) имеет следующий вид:
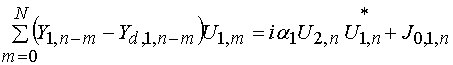 , (17)
, (17)
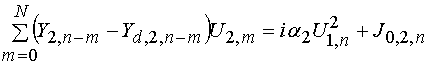 ,
, ![]() .
.
В качестве первого
шага преобразований системы (17) рассмотрим оператор, стоящий в левой части.
Считаем, что индекс ![]() меняется
от минус до плюс бесконечности. Это возможно сделать при выполнении условия:
меняется
от минус до плюс бесконечности. Это возможно сделать при выполнении условия:
![]() , при
, при ![]() ,
, ![]() .
.
Нетрудно показать, что справедливо следующее равенство:
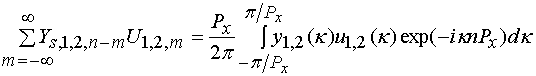 , (18)
, (18)
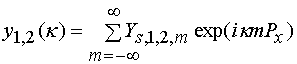 ,
,
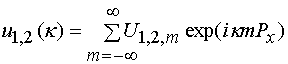 ,
,
![]() .
.
Из соотношений (18)
видно, что функция ![]() является
дискретным преобразованием Фурье последовательности
является
дискретным преобразованием Фурье последовательности ![]() . Аналогичные утверждения
справедливы для
. Аналогичные утверждения
справедливы для ![]() ,
а также для
,
а также для ![]() и
и
![]() .
.
Конкретизируем далее
отмеченное выше свойство медленного изменения параметров волн в ЭМК в режиме
пространственного синхронизма. Оно состоит в том, что ![]() можно представить в следующем виде:
можно представить в следующем виде:
![]() , (19)
, (19)
где ![]() - постоянные распространения
собственных волн линейного ЭМК на частотах соответственно
- постоянные распространения
собственных волн линейного ЭМК на частотах соответственно ![]() и
и ![]() . Непосредственно на частоте
пространственного синхронизма они связаны соотношением
. Непосредственно на частоте
пространственного синхронизма они связаны соотношением ![]() . При этом, если синхронизм
реализуется по методу скомпенсированной емкости, то
. При этом, если синхронизм
реализуется по методу скомпенсированной емкости, то ![]() .
.
Экспоненциальный
множитель в формуле (19) описывает быстрые изменения напряжений на элементах ЭМК,
а множитель ![]() медленные
изменения, представляющие наибольший интерес. Из вида соотношения (19) следует,
что дискретное преобразование Фурье таких последовательностей сосредоточено в
небольшой окрестности точки
медленные
изменения, представляющие наибольший интерес. Из вида соотношения (19) следует,
что дискретное преобразование Фурье таких последовательностей сосредоточено в
небольшой окрестности точки ![]() . Поэтому в соотношении (18) мы можем
вместо точного выражения для функций
. Поэтому в соотношении (18) мы можем
вместо точного выражения для функций ![]() использовать их приближенные
представления, справедливые только в окрестности указанной выше точки:
использовать их приближенные
представления, справедливые только в окрестности указанной выше точки:
![]() , (20)
, (20)
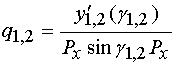 ,
,
где ![]() - производные от соответствующих
функций.
- производные от соответствующих
функций.
Подставляя соотношения (20) в выражения (18), получаем:
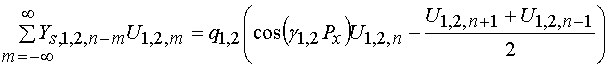 .
.
(21)
Из условия медленного
изменения амплитуд ![]() можно
записать следующие приближенные равенства:
можно
записать следующие приближенные равенства:
![]() , (22)
, (22)
![]() ,
,
![]() .
.
С учетом формул (22) получаем окончательное выражение для исследуемого оператора:
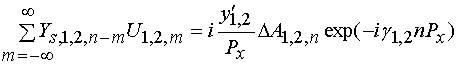 . (23)
. (23)
Строго говоря, соотношение (23) справедливо при бесконечных пределах суммирования. Однако мы будем применять его для анализа ЭМК конечных размеров, принимая во внимание, что концевые эффекты, связанные с конечностью ЭМК будут сказываться только на небольшом числе элементов структуры, расположенных на ее краях. Кроме того, из дальнейшего анализа будет ясно, что эти эффекты весьма малы даже на границах ЭМК.
Анализ аналогичный представленному выше можно провести для свободного члена уравнений (17):
![]() ,
,
где
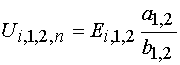 ,
,
![]() =
=![]() .
.
Выражения
(24) и (25) записаны для случая, когда ЭМК возбуждается на обеих рассматриваемых
частотах плоскими Т – волнами ПВ. Амплитуды электрических полей этих волн равны
![]() . Они не
зависят от координаты
. Они не
зависят от координаты ![]() и,
следовательно, от индекса
и,
следовательно, от индекса ![]() . В этом случае возникает вопрос о смысле
индекса
. В этом случае возникает вопрос о смысле
индекса ![]() во
втором равенстве из (25). На первый взгляд он не нужен, так как в правой части
стоят величины не зависящие от него. Однако это не совсем так. Поскольку речь
пошла о возбуждении, то это означает автоматически, что мы рассматриваем ЭМК
конечной длины или, по крайней мере, полубесконечный ЭМК. Это означает, что
элементы векторов
во
втором равенстве из (25). На первый взгляд он не нужен, так как в правой части
стоят величины не зависящие от него. Однако это не совсем так. Поскольку речь
пошла о возбуждении, то это означает автоматически, что мы рассматриваем ЭМК
конечной длины или, по крайней мере, полубесконечный ЭМК. Это означает, что
элементы векторов ![]() отличны
от нуля только при
отличны
от нуля только при ![]() .
С учетом этого факта можно привести более правильное определение для
последовательности
.
С учетом этого факта можно привести более правильное определение для
последовательности ![]() :
:
Соотношение (26)
приводит к следующему выражению для ![]() :
:
![]() , (27)
, (27)
где ![]() - символ Кронекера. Для
полубесконечного ЭМК второе слагаемое в формуле (27) отсутствует.
- символ Кронекера. Для
полубесконечного ЭМК второе слагаемое в формуле (27) отсутствует.
Отметим дополнительно
также то, что при выводе (24) и (25) принято во внимание, что дискретное
преобразование Фурье от последовательностей ![]() имеет нули при
имеет нули при ![]() . В этом нет ничего
удивительного, так как нули этой функции совпадают с постоянными
распространения собственных волн ПВ, в число которых входит Т – волна, имеющая
на соответствующих частотах постоянные распространения равные
. В этом нет ничего
удивительного, так как нули этой функции совпадают с постоянными
распространения собственных волн ПВ, в число которых входит Т – волна, имеющая
на соответствующих частотах постоянные распространения равные ![]() .
.
С учетом выполненных выше преобразований получаем следующую систему разностных уравнений:
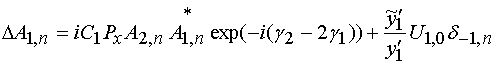 , (28)
, (28)
 ,
,
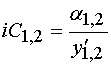 .
.
Уравнения (28) получены для полубесконечного ЭМК. Непосредственно на частоте пространственного синхронизма выполняются следующие соотношения:
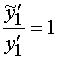 , (29)
, (29)
![]() ,
,
![]() .
.
В справедливости
последнего соотношения из (29) можно убедиться, непосредственно вычисляя
коэффициенты ![]() .
Равенства (29) позволяют упростить систему (28):
.
Равенства (29) позволяют упростить систему (28):
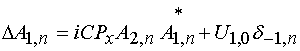 , (30)
, (30)
![]() .
.
Уравнения (28) и (30)
можно использовать для непосредственного итерационного решения. При этом
следует иметь ввиду, что ![]() при
при ![]() . С учетом этого обстоятельства слагаемые в
правой части системы (30) можно рассматривать в качестве начальных условий
итерационного процесса.
. С учетом этого обстоятельства слагаемые в
правой части системы (30) можно рассматривать в качестве начальных условий
итерационного процесса.
Для аналитического
исследования решения граничной задачи разностные уравнения (30) можно
приближенно преобразовать к дифференциальным уравнениям. Такое преобразование
справедливо, вообще говоря, в пределе при ![]() . Однако, принимая во внимание медленное
изменение амплитуд
. Однако, принимая во внимание медленное
изменение амплитуд ![]() ,
мы можем совершить указанный переход при конечном периоде ЭМК. Для этого
сделаем следующие замены:
,
мы можем совершить указанный переход при конечном периоде ЭМК. Для этого
сделаем следующие замены:
![]() , (31)
, (31)
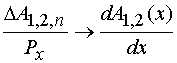 ,
,
![]() .
.
Таким образом, мы приходим к системе двух нелинейных дифференциальных уравнений первого порядка:
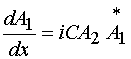 , (32)
, (32)
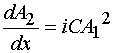
с концевыми условиями:
![]() .
.
Система дифференциальных уравнений (32) хорошо известна в теории нелинейных волн [2]. Мы не будем ставить перед собой задачу поиска новых аналитических решений, а будем использовать уравнения (32) и известные их решения для получения простых количественных оценок параметров процессов распространения волн в ЭМК в режиме пространственного синхронизма.
4. Качественная характеристика и результаты численного исследования волновых процессов в режиме пространственного синхронизма сонаправленных волн
Рассмотрим поведение электромагнитных волн в наиболее интересной ситуации, когда условия пространственного синхронизма выполняются абсолютно точно. С помощью итерационной схемы, представленной в разделе 3 был проведен цикл численных исследований. Его результаты можно разделить на две группы. Первая группа – это качественное описание режимов распространения электромагнитных волн. Вторая группа – это количественные характеристики процессов, полученные численно. Рассмотрим обе группы в данном разделе. В следующем части работы мы попытаемся с помощью аналитического решения системы дифференциальных уравнений (32) получить ряд простых соотношений для параметров волновых процессов, достаточно хорошо совпадающих с численными результатами раздела 4.
На рис.
10-13 показаны распределения модулей амплитуд волн на первой и второй
гармониках ![]() .
Кривая 1 на рис. 10-13 соответствует первой, а кривая 2 второй гармонике.
Графики получены для следующих параметров структуры:
.
Кривая 1 на рис. 10-13 соответствует первой, а кривая 2 второй гармонике.
Графики получены для следующих параметров структуры: ![]() пФ/В,
пФ/В, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ГГц.
ГГц.
Возбуждающие
ЭМК волны описывались следующим образом. Пусть ![]() - амплитуды этих волн (индексы 1,2
соответствуют первой и второй гармоникам частоты). Введем следующие параметры:
- амплитуды этих волн (индексы 1,2
соответствуют первой и второй гармоникам частоты). Введем следующие параметры:
![]() , (33)
, (33)
 ,
,
![]() .
.
Графики на
рис. 10-13 соответствуют следующим значениям введенных в соотношении (33)
параметров: ![]() ,
, ![]() , 100, 1.25, 0.01.
, 100, 1.25, 0.01.
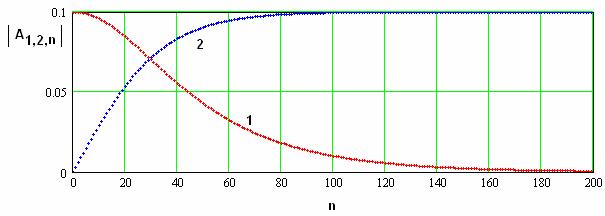
Рис. 10. Распределение модулей амплитуд волн в режиме генерации второй гармоники.
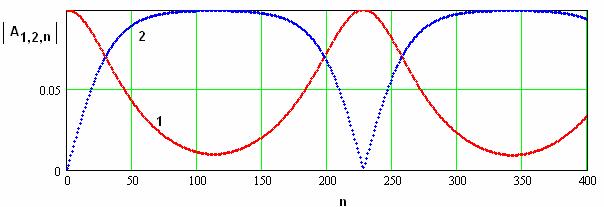
Рис. 11. Распределение модулей амплитуд волн в режиме усиления второй гармоники.
Рис. 12. Распределение модулей амплитуд волн в промежуточном режиме.
Рис. 13. Распределение модулей амплитуд волн в режиме усиления первой гармоники.
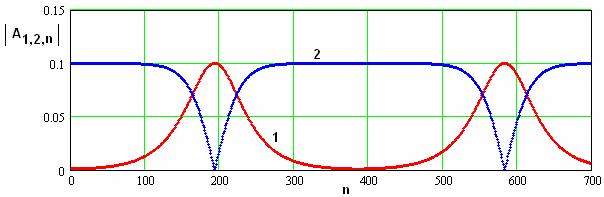
Из рис. 10-13 видно,
что параметром, определяющим характер взаимодействия волн в ЭМК является
отношение модулей амплитуд падающих волн ![]() .
.
При ![]() (см. рис. 10), что
наблюдается, когда
(см. рис. 10), что
наблюдается, когда ![]() =0,
мы имеем режим генерации второй гармоники, который характеризуется перекачкой
энергии с частоты
=0,
мы имеем режим генерации второй гармоники, который характеризуется перекачкой
энергии с частоты ![]() на
частоту
на
частоту ![]() . Этот
процесс непериодический. Обратная перекачка с частоты
. Этот
процесс непериодический. Обратная перекачка с частоты ![]() на частоту
на частоту ![]() не происходит.
не происходит.
Большие, но
конечные значения параметра ![]() соответствуют режиму усиления второй
гармоники. В этом режиме малый сигнал удвоенной частоты усиливается за счет
взаимодействия с сильным сигналом на частоте
соответствуют режиму усиления второй
гармоники. В этом режиме малый сигнал удвоенной частоты усиливается за счет
взаимодействия с сильным сигналом на частоте ![]() . Процесс имеет квазипериодический характер
(вопрос о периодичности мы еще будем обсуждать ниже, а сейчас ограничимся
использованием термина квазипериодический, который говорит о том, что процесс
близок к периодическому, но не полностью тождественен ему). Отметим также, что
распределение модулей амплитуд имеет существенно негармонический характер.
. Процесс имеет квазипериодический характер
(вопрос о периодичности мы еще будем обсуждать ниже, а сейчас ограничимся
использованием термина квазипериодический, который говорит о том, что процесс
близок к периодическому, но не полностью тождественен ему). Отметим также, что
распределение модулей амплитуд имеет существенно негармонический характер.
При
значениях ![]() порядка
единицы ЭМК находится в промежуточном режиме. Распределение модулей амплитуд
квазипериодическое и близкое к гармоническому.
порядка
единицы ЭМК находится в промежуточном режиме. Распределение модулей амплитуд
квазипериодическое и близкое к гармоническому.
Последний
режим – это режим параметрического усиления первой гармоники, который имеет
место при ![]() . В
этом случае процесс имеет квазипериодический и негармонический характер.
. В
этом случае процесс имеет квазипериодический и негармонический характер.
Рассмотрим далее
некоторые результаты численного исследования процесса распространения
электромагнитных волн в нелинейном ЭМК в условиях пространственного
синхронизма. На рис. 14 а,б показаны типичные распределения модулей амплитуд
волн первой и второй гармоник в режиме параметрического усиления (рис. 14 а) и
усиления второй гармоники (рис. 14 б). Также на рис. 14 а,б поясняются
параметры, с помощью которых мы будем количественно описывать исследуемые процессы.
К их числу относятся период процесса ![]() , координата точки первого максимума
, координата точки первого максимума ![]() , максимальные и
минимальные значения модулей амплитуд первой и второй гармоник.
, максимальные и
минимальные значения модулей амплитуд первой и второй гармоник.
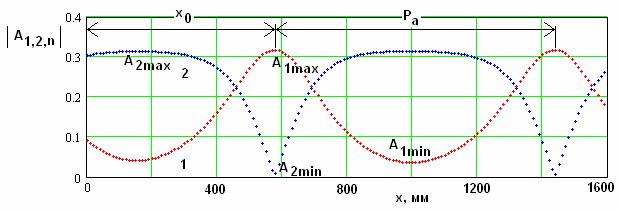
а
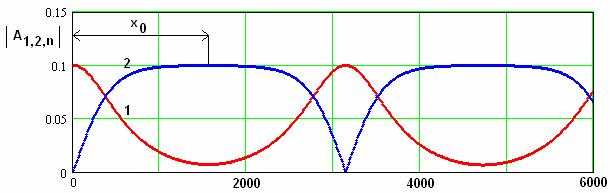
б
Рис. 14. К определению параметров процесса в режимах усиления первой и второй гармоник.
Отметим, что
координата ![]() определяется
по-разному в режимах усиления первой и второй гармоник. В первом случае,
который соответствует неравенству
определяется
по-разному в режимах усиления первой и второй гармоник. В первом случае,
который соответствует неравенству ![]() параметр
параметр ![]() описывает расстояние от начала координат
то точки максимума первой гармоники, а во втором случае (
описывает расстояние от начала координат
то точки максимума первой гармоники, а во втором случае (![]() ) до точки максимума второй
гармоники. Таким образом, в обоих режимах мы можем с помощью параметра
) до точки максимума второй
гармоники. Таким образом, в обоих режимах мы можем с помощью параметра ![]() можем описывать
расстояние, на котором происходит максимальная перекачка энергии из гармоники с
большей начальной амплитудой в гармонику с меньшей начальной амплитудой.
можем описывать
расстояние, на котором происходит максимальная перекачка энергии из гармоники с
большей начальной амплитудой в гармонику с меньшей начальной амплитудой.
На рис.
15, 16 представлены зависимости координаты первого максимума ![]() и периода
и периода ![]() от параметра
от параметра ![]() , который определяется
разностью фаз между волнами, возбуждающими ЭМК. Указанные зависимости получены
при
, который определяется
разностью фаз между волнами, возбуждающими ЭМК. Указанные зависимости получены
при ![]() ,
, ![]() пФ,
пФ, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ГГц. Кривые 1 – 5 на обоих рисунках
соответствуют q=0.0001, 0.001, 0.01, 0.1, 0.4.
Таким образом, мы можем сделать вывод о том, что представленные графики
получены в режиме усиления первой гармоники.
ГГц. Кривые 1 – 5 на обоих рисунках
соответствуют q=0.0001, 0.001, 0.01, 0.1, 0.4.
Таким образом, мы можем сделать вывод о том, что представленные графики
получены в режиме усиления первой гармоники.
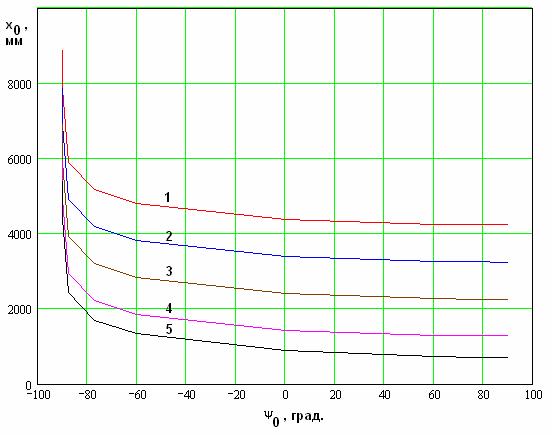
Рис. 15. Координата первого максимума первой гармоники.
Параметр ![]() меняется от минус до
плюс
меняется от минус до
плюс ![]() . Этого
интервала достаточно для полного описания поведения функций
. Этого
интервала достаточно для полного описания поведения функций ![]() и
и ![]() , так как они удовлетворяют следующим
соотношениям:
, так как они удовлетворяют следующим
соотношениям:
![]() , (34)
, (34)
![]() .
.

Рис. 16. Период процесса в режиме параметрического усиления.
Обращает на себя
внимание присутствие точек, в которых параметры ![]() и
и ![]() резко растут. Ниже будет показано, что они
уходят на бесконечность. Это происходит при
резко растут. Ниже будет показано, что они
уходят на бесконечность. Это происходит при ![]() =
=![]() . Таким образом, при некоторой разности фаз
возбуждающих ЭМК волн процесс становится апериодическим. При этом при
. Таким образом, при некоторой разности фаз
возбуждающих ЭМК волн процесс становится апериодическим. При этом при ![]() =
=![]() усиление первой гармоники
сохраняется, так как
усиление первой гармоники
сохраняется, так как ![]() остается
конечной величиной, а при
остается
конечной величиной, а при ![]() =
=![]() усиление отсутствует, поскольку
усиление отсутствует, поскольку ![]() .
.
Скорость перекачки
энергии из второй гармоники в первую зависит от амплитуды первой гармоники на
входе ЭМК, которая характеризуется параметром ![]() . Из рис. 15 хорошо видно, что расстояние
. Из рис. 15 хорошо видно, что расстояние ![]() уменьшается с ростом
уменьшается с ростом ![]() .
.
Режим усиления второй
гармоники характеризуется графиками, показанными на рис. 17 и 18. На них
представлены зависимости координаты ![]() и периода
и периода ![]() от параметра
от параметра ![]() . Кривые 1 – 5 соответствуют q = 4, 10, 100, 1000, 10000. Остальные параметры ЭМК
такие же как и раньше.
. Кривые 1 – 5 соответствуют q = 4, 10, 100, 1000, 10000. Остальные параметры ЭМК
такие же как и раньше.
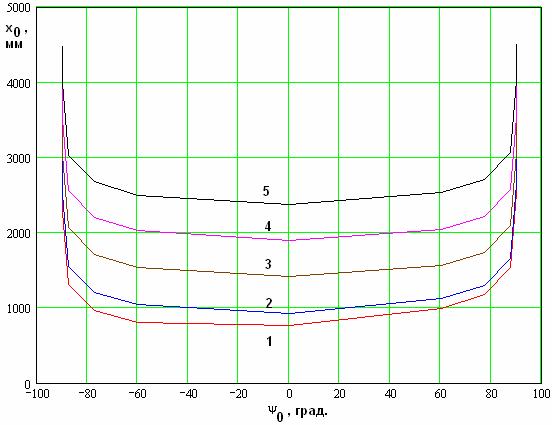
Рис. 17. Координата первого максимума второй гармоники.
Основное отличие
режима усиления второй гармоники от рассмотренного выше усиления первой
гармоники состоит в том, что усиление теперь отсутствует при ![]() =
=![]() . Процесс при этих значениях фаз
возбуждающих волн имеет апериодический характер.
. Процесс при этих значениях фаз
возбуждающих волн имеет апериодический характер.
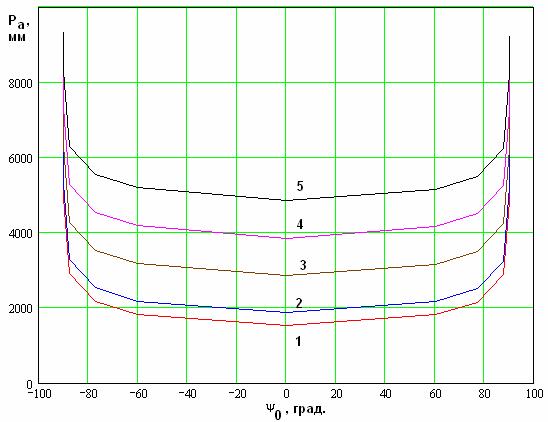
Рис. 18. Период процесса в режиме усиления второй гармоники.
Интересные
закономерности позволяет установить анализ макисмальных и минимальных значений
амплитуд первой и второй гармоник ![]() в промежуточном режиме. На рис. 19 и 20
показаны их зависимости от параметра
в промежуточном режиме. На рис. 19 и 20
показаны их зависимости от параметра ![]() при
при ![]() =0.9. Кривая 1 соответствует максимальному
значению, а кривая 2 минимальному. Первой гармонике соответствует рис. 18, а
второй рис. 19.
=0.9. Кривая 1 соответствует максимальному
значению, а кривая 2 минимальному. Первой гармонике соответствует рис. 18, а
второй рис. 19.
Из рис. 19 и 20
видно, что ![]() являются
периодическими функциями
являются
периодическими функциями ![]() с периодом равным
с периодом равным ![]() . При
. При ![]() =
=![]() минимальное значение амплитуды равно нулю,
а максимальное
минимальное значение амплитуды равно нулю,
а максимальное ![]() .
Они не меняются при изменении
.
Они не меняются при изменении ![]() . Это означает, что процесс имеет
непериодический характер. При
. Это означает, что процесс имеет
непериодический характер. При ![]() =0,
=0,![]() пульсации амплитуд минимальны. Интересно,
что их величина зависит от параметра
пульсации амплитуд минимальны. Интересно,
что их величина зависит от параметра ![]() . При
. При ![]() они вообще исчезают.
они вообще исчезают.

Рис. 19.
Зависимость максимальных и минимальных значений амплитуды первой гармоники от
параметра ![]() .
.
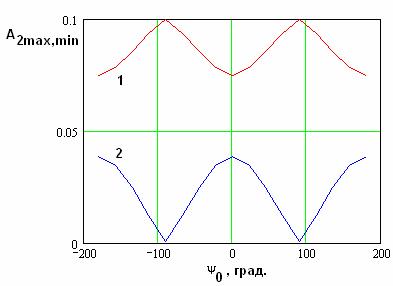
Рис. 20.
Зависимость максимальных и минимальных значений амплитуды второй гармоники от
параметра ![]() .
.
Об этом эффекте
наиболее наглядно свидетельствуют графики зависимости ![]() от переменной
от переменной ![]() , которые показаны на
рис. 21 и 22. Кривые 1 – 3 соответствуют максимальному значению амплитуды. Они
получены для
, которые показаны на
рис. 21 и 22. Кривые 1 – 3 соответствуют максимальному значению амплитуды. Они
получены для ![]() =-22.5,
0, 450. Кривые 1’-3’ получены для тех же значений
=-22.5,
0, 450. Кривые 1’-3’ получены для тех же значений ![]() , но они соответствуют
минимальным значениям амплитуды.
, но они соответствуют
минимальным значениям амплитуды.
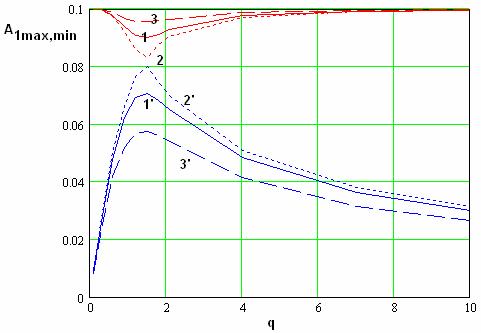
Рис. 21.
Зависимость максимальных и минимальных значений амплитуды первой гармоники от
параметра ![]() .
.
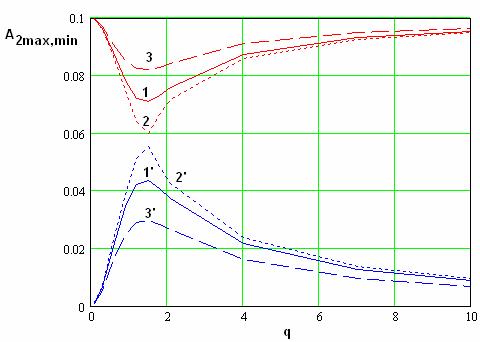
Рис. 22.
Зависимость максимальных и минимальных значений амплитуды второй гармоники от
параметра ![]() .
.
Из рис. 21, 22 видно,
что максимальное и минимальное значения амплитуд первой и второй гармоник
сближаются и при ![]() совпадают
друг с другом. Полное совпадение означает, что амплитуды практически не
меняются вдоль оси 0х. Характерно, что абсолютные значения амплитуд волн на
первой и второй гармониках частоты отличаются друг от друга.
совпадают
друг с другом. Полное совпадение означает, что амплитуды практически не
меняются вдоль оси 0х. Характерно, что абсолютные значения амплитуд волн на
первой и второй гармониках частоты отличаются друг от друга.
Решение в режиме генерации второй гармоники имеет апериодический характер. Энергия волны на основной частоте переходит в волну на удвоенной частоте. Обратной перекачки энергии не возникает.
Приведенные выше
численные данные получены для фиксированного значения параметра ![]() , который пропорционален
суммарной мощности, переносимой волнами в ЭМК. Из теории нелинейных волн
известно [2], что он влияет только на скорость процесса, которая определяется
произведением
, который пропорционален
суммарной мощности, переносимой волнами в ЭМК. Из теории нелинейных волн
известно [2], что он влияет только на скорость процесса, которая определяется
произведением ![]() .
Численные исследования показывают, что такой характер влияния сохраняется и в
случае ЭМК.
.
Численные исследования показывают, что такой характер влияния сохраняется и в
случае ЭМК.
5. Аналитическое исследование волновых процессов в режиме пространственного синхронизма
Целью аналитического исследования является вывод достаточно простых соотношений, дающих, без использования численных расчетов, количественную характеристику волновых процессов в режиме пространственного синхронизма. Эту задачу решим с помощью модели в виде системы дифференциальных уравнений (32). Как уже отмечалось выше, частные решения этой системы известны [2]. Мы попытаемся, используя их, получить приближенную модель квазипериодических процессов, изученных численно в разделе 4.
Будем использовать три частных решения: решение в гиперболических функциях, два решения при заданной накачки и решение в виде квазисобственных волн. Приведем их без подробного анализа.
Решение в гиперболических функциях:
![]() ,
,
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() - постоянные, с точностью до которых
определяется решение однородной системы дифференциальных уравнений (32). Их
можно определить из начальных условий. Нетрудно показать, что
- постоянные, с точностью до которых
определяется решение однородной системы дифференциальных уравнений (32). Их
можно определить из начальных условий. Нетрудно показать, что
![]() .
.
Отсюда следует, что
постоянная ![]() равна
равна
![]() . Таким
образом, она определяется мощностью, поступившей на вход ЭМК. Если ввести
аналогично соотношению (33) параметр
. Таким
образом, она определяется мощностью, поступившей на вход ЭМК. Если ввести
аналогично соотношению (33) параметр ![]() , то можно увидеть, что для решения в
гиперболических функциях он равен
, то можно увидеть, что для решения в
гиперболических функциях он равен ![]() .
.
Решение при
постоянной накачке на второй гармонике. Это решение получается из системы
уравнений (32) при условии, что ![]() , которое может приближенно выполняться при
, которое может приближенно выполняться при
![]() . В этом
случае система (32) сводится к следующей системе дифференциальных уравнений:
. В этом
случае система (32) сводится к следующей системе дифференциальных уравнений:
 , (36)
, (36)
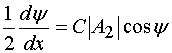 .
.
Система (36) имеет следующее решение:
![]() ,
,
где ![]() - действительные числа,
определяемые из начальных условий.
- действительные числа,
определяемые из начальных условий.
Решение при
постоянной накачке на первой гармонике соответствует условию ![]() , которой может
выполняться при
, которой может
выполняться при ![]() .
Это решение элементарно получается из второго уравнения системы (32):
.
Это решение элементарно получается из второго уравнения системы (32):
![]() , (38)
, (38)
где ![]() - постоянная интегрирования
дифференциального уравнения. Ее можно записать следующим образом:
- постоянная интегрирования
дифференциального уравнения. Ее можно записать следующим образом:
![]() .
.
Тогда решение (38) приобретает удобный вид:
Решение в виде квазисобственных волн. Это частное решение системы (32) получается, если его искать в следующем виде:
![]() ,
,
![]() ,
,
где ![]() - постоянные, не зависящие от
координаты
- постоянные, не зависящие от
координаты ![]() , а
, а
![]() имеет смысл
постоянной распространения квазисобственной волны. Из системы (32) можно
получить следующие соотношения:
имеет смысл
постоянной распространения квазисобственной волны. Из системы (32) можно
получить следующие соотношения:
 ,
,
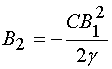 . (40)
. (40)
Из соотношений для комплексных величин (40) следуют два равенства для модулей и фаз:
Режим генерации
второй гармоники, в котором ![]() можно точно описать решением в
гиперболических функциях:
можно точно описать решением в
гиперболических функциях:
 , (42)
, (42)
![]() ,
,
![]() .
.
В соотношениях (42)
параметр ![]() можно
заменить
можно
заменить ![]() так
как
так
как ![]() . Таким образом,
мы можем сделать вывод о том, что скорость перекачки энергии первой гармоники
во вторую определяется параметром
. Таким образом,
мы можем сделать вывод о том, что скорость перекачки энергии первой гармоники
во вторую определяется параметром ![]() , о котором говорилось выше.
, о котором говорилось выше.
Численное решение и аналитическая модель (42) дают практически одинаковые результаты. Этот вывод можно сделать из рис. 23, на котором показаны распределения модулей амплитуд волн на первой и второй гармониках.
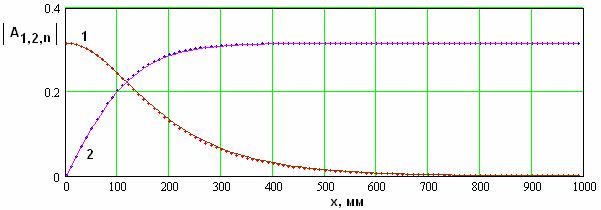
Рис. 23. Распределения модулей амплитуд волн, полученные из численной и аналитической моделей.
Они получены при ![]() . Другие параметры такие
же, как и в приведенных выше численных примерах. Кривые 1 и 2 соответствуют
первой и второй гармоникам. Точки показывают результаты численного решения, а
сплошные кривые аналитического.
. Другие параметры такие
же, как и в приведенных выше численных примерах. Кривые 1 и 2 соответствуют
первой и второй гармоникам. Точки показывают результаты численного решения, а
сплошные кривые аналитического.
Рассмотрим далее
режим параметрического усиления первой гармоники. Будем анализировать ситуацию,
при которой амплитуда возбуждающей волны на основной частоте много меньше
амплитуды волны на удвоенной частоте: ![]() , что эквивалентно неравенству
, что эквивалентно неравенству ![]() . Опишем поведение
амплитуд
. Опишем поведение
амплитуд ![]() комбинацией
решения в гиперболических функциях и решения с заданной накачкой на второй
гармонике.
комбинацией
решения в гиперболических функциях и решения с заданной накачкой на второй
гармонике.
Из рис. 13 хорошо
видно, что на начальном участке функцию ![]() действительно можно считать постоянной.
Поэтому для описания функции
действительно можно считать постоянной.
Поэтому для описания функции ![]() допустимо использовать решение (37). В
области первого максимума амплитуды волны на первой гармонике целесообразно
использовать решение в гиперболических функциях. При этом неизвестные константы
решения (37) будем выбирать исходя из начальных условий, а неизвестные
константы в (35) найдем из условий сшивания соотношений (35) и (37).
допустимо использовать решение (37). В
области первого максимума амплитуды волны на первой гармонике целесообразно
использовать решение в гиперболических функциях. При этом неизвестные константы
решения (37) будем выбирать исходя из начальных условий, а неизвестные
константы в (35) найдем из условий сшивания соотношений (35) и (37).
Наложение начальных условий приводит к следующим соотношениям:
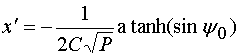 , (43)
, (43)
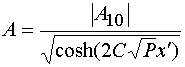 .
.
В формулах (43)
величина ![]() заменена
более удобным параметром
заменена
более удобным параметром ![]() , к которому она близка при принятых
соотношениях между амплитудами волн, возбуждающих ЭМК.
, к которому она близка при принятых
соотношениях между амплитудами волн, возбуждающих ЭМК.
Теперь перейдем к сшиванию
двух решений. При ![]() решение
(37) имеет следующее асимптотическое поведение:
решение
(37) имеет следующее асимптотическое поведение:
![]() , (44)
, (44)
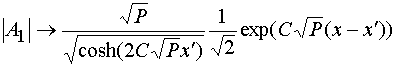 .
.
Рассмотрим решение в
гиперболических функциях для амплитуды ![]() :
:
![]() ,
,
![]() .
.
Исходим из
условия ![]() .
Тогда при малых значениях
.
Тогда при малых значениях ![]() гиперболический тангенс приближенно равен
минус единице:
гиперболический тангенс приближенно равен
минус единице:
![]() . (45)
. (45)
При ![]() должно выполняться
начальное условие для
должно выполняться
начальное условие для ![]() ,
которое с учетом того, что
,
которое с учетом того, что ![]() позволяет определить постоянную
позволяет определить постоянную ![]() :
:
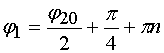 ,
, ![]() (46)
(46)
Таким
образом, мы выразили фазы амплитуд волн, описываемых решением в гиперболических
функциях через фазу возбуждающей волны ![]() . Из формулы (46) следует выражение для
параметра
. Из формулы (46) следует выражение для
параметра ![]() :
:
![]() . (47)
. (47)
Сравнивая
выражения (44) и (47), можно сделать вывод, что они совпадают при ![]() .
.
Далее рассмотрим решение в гиперболических функциях для первой гармоники:
 .
.
При малых ![]() оно имеет
экспоненциальный вид:
оно имеет
экспоненциальный вид:
![]() . (47)
. (47)
Сравнивая
выражения (44) и (47), приравняем множители при экспонентах ![]() и найдем неизвестный
параметр
и найдем неизвестный
параметр ![]() :
:
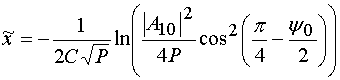 . (48)
. (48)
Этот
параметр является расстоянием от начала координат до точки первого максимума
амплитуды первой гармоники частоты. Как видно из рис. 14 а он равен ![]() . Из того же рис. 14 а
нетрудно увидеть, что период процесса равен удвоенной разности между
координатами
. Из того же рис. 14 а
нетрудно увидеть, что период процесса равен удвоенной разности между
координатами ![]() и
и
![]() , где
, где ![]() - это координата точки
минимума указанной амплитуды. Таким образом, для периода
- это координата точки
минимума указанной амплитуды. Таким образом, для периода ![]() получаем следующее выражение:
получаем следующее выражение:
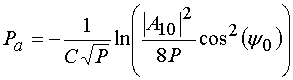 . (49)
. (49)
На рис. 24
и 25 показаны зависимости расстояния ![]() и периода
и периода ![]() от параметра
от параметра ![]() . Сплошные кривые получены с помощью
аналитических формул. Точки соответствуют численным расчетам. Кривые 1 – 4
построены для
. Сплошные кривые получены с помощью
аналитических формул. Точки соответствуют численным расчетам. Кривые 1 – 4
построены для ![]() 0.0001,
0.001, 0.01, 0.1. Исходные формулы (48), (49) дают погрешность (1 – 2)%. Для
устранения этой погрешности в данные соотношения введены корректирующие
множители:
0.0001,
0.001, 0.01, 0.1. Исходные формулы (48), (49) дают погрешность (1 – 2)%. Для
устранения этой погрешности в данные соотношения введены корректирующие
множители:
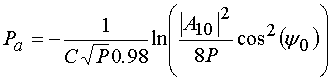 .
.
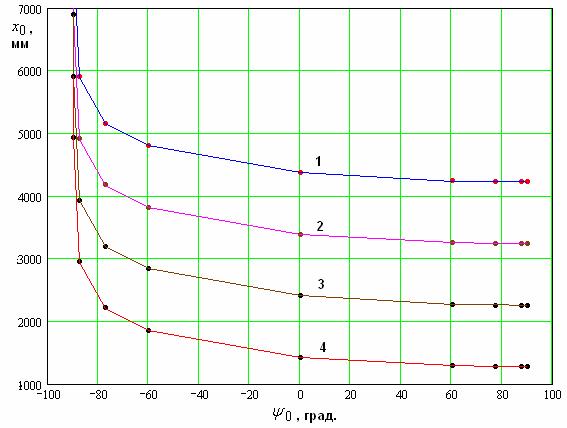
Рис.
24. Зависимость расстояния![]() от параметра
от параметра ![]() .
.
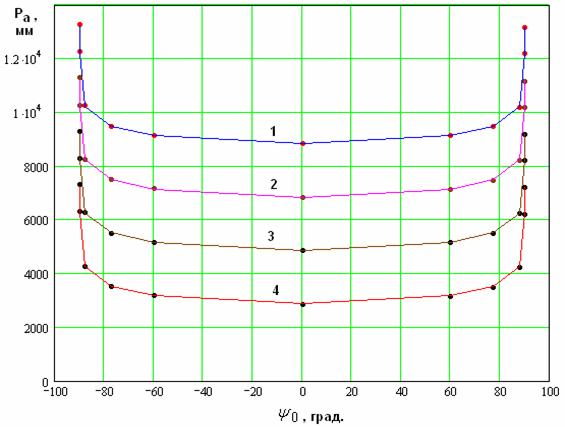
Рис.
25. Зависимость периода ![]() от параметра
от параметра ![]() .
.
Как видно из рис. 24, 25, введение корректирующих множителей существенно уменьшает расхождение численных и аналитических результатов.
Рассмотрим
далее режим усиления второй гармоники, возникающий при ![]() . В этом режиме построит
полноценную аналитическую модель, описывающую процессы в ЭМК вплоть до первого
максимума второй гармоники затруднительно. Однако для периода процесса удалось
получить на основе аппроксимации численных данных следующую формулу, очень
похожую на соотношение (50):
. В этом режиме построит
полноценную аналитическую модель, описывающую процессы в ЭМК вплоть до первого
максимума второй гармоники затруднительно. Однако для периода процесса удалось
получить на основе аппроксимации численных данных следующую формулу, очень
похожую на соотношение (50):
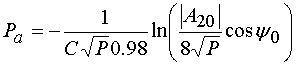 . (51)
. (51)
Она обеспечивает удовлетворительную точность. Об этом можно судить из графиков, показанных на рис. 26.

Рис. 26. Период процесса в режиме усиления второй гармоники.
Кривые 1-4 получены
для ![]() 10, 100,
1000, 10000. Напомним, что другие параметры ЭМК остаются неизменными для всех
рассматриваемых численных примеров.
10, 100,
1000, 10000. Напомним, что другие параметры ЭМК остаются неизменными для всех
рассматриваемых численных примеров.
Для вывода
соотношений, описывающих параметр ![]() необходимо подробнее рассмотреть
распределения модулей амплитуд
необходимо подробнее рассмотреть
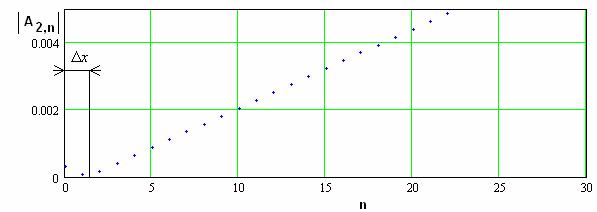
распределения модулей амплитуд ![]() . Они показаны на рис. 27 а,б.
. Они показаны на рис. 27 а,б.

а
б
Рис. 27. Амплитудные распределения в режиме усиления второй гармоники.
Кривые получены при ![]() 100,
100, ![]() ,
, ![]() . На рис. 27 а показаны распределения в
крупном масштабе, а на рис. 27 б распределение
. На рис. 27 а показаны распределения в
крупном масштабе, а на рис. 27 б распределение ![]() , но на начальном участке. Из рис. 27 а,б
видно, что расстояние
, но на начальном участке. Из рис. 27 а,б
видно, что расстояние ![]() можно
представить следующим образом:
можно
представить следующим образом:
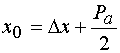 , (52)
, (52)
где ![]() - координата точки минимума
модуля амплитуды
- координата точки минимума
модуля амплитуды ![]() .
Отметим, что координата
.
Отметим, что координата ![]() может иметь также и отрицательные
значения.
может иметь также и отрицательные
значения.
Для вывода
соотношения, описывающего координату ![]() воспользуемся решением (39) системы
дифференциальных уравнений, которое соответствует условию
воспользуемся решением (39) системы
дифференциальных уравнений, которое соответствует условию ![]() . В нем имеется неизвестная
величина
. В нем имеется неизвестная
величина ![]() ,
которую ищем из начальных условий при
,
которую ищем из начальных условий при ![]() :
:
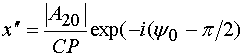 . (53)
. (53)
При записи выражения
(53) принято во внимание, что при ![]()
![]() .
.
Подставляя
соотношение (53) в решение (39), находим координату точки, в которой его модуль
имеет минимальное значение. Эта координата совпадает с ![]() :
:
 . (54)
. (54)
С помощью формулы
(54) не составляет труда определить расстояние ![]() .
.
Промежуточный режим
представляет наибольшие трудности для аналитического исследования, так как в
нем форма амплитудного распределения меняется весьма существенно в зависимости
от начального значения параметра ![]() и параметра
и параметра ![]() . Имеет смысл выделить режим возбуждения
квазисобственных волн, который наблюдается при выполнении условий, следующих из
соотношений (41):
. Имеет смысл выделить режим возбуждения
квазисобственных волн, который наблюдается при выполнении условий, следующих из
соотношений (41):
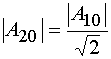 ,
, ![]() . (55)
. (55)
В этом режиме модули
амплитуд ![]() не
зависят от координаты
не
зависят от координаты ![]() .
При небольших отклонениях от условий (55) распределения модулей амплитуд имеют
вид осциллирующих функций (см. рис. 12).
.
При небольших отклонениях от условий (55) распределения модулей амплитуд имеют
вид осциллирующих функций (см. рис. 12).
6. Генерация второй гармоники в режиме пространственного синхронизма волн разных типов
Возможность пространственного синхронизма волн ЭМК разных типов была установлена в разделе 2. Кратко рассмотрим результаты численного исследования этого режима. Мы не можем претендовать на полноту полученных результатов. Они говорят только о том, что интенсивная генерация второй гармоники в данном режиме в принципе возможна. Численные результаты, которые будут представлены ниже получены путем непосредственного решения системы нелинейных уравнений (3). Это накладывает ограничения на возможности увеличения числа элементов ЭМК. Имеются также ограничения на напряжение волны, возбуждающей ЭМК, которые связаны с неустойчивостью итерационного процесса решения системы (3).
На рис. 28
а,б и 29 а,б показаны распределения модулей амплитуд напряжений и токов в ЭМК
со следующими параметрами: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Возбуждался ЭМК волной на частотах 7.69
ГГц (см. рис. 28 а,б) и 8.2 ГГц (см. рис. 29 а,б).
. Возбуждался ЭМК волной на частотах 7.69
ГГц (см. рис. 28 а,б) и 8.2 ГГц (см. рис. 29 а,б).
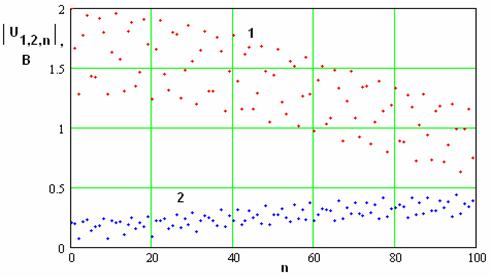
а
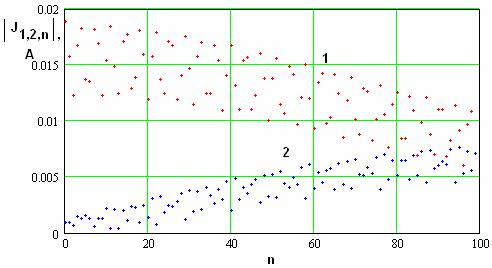
б
Рис. 28. Распределения модулей амплитуд напряжений и токов на частоте 7.69 ГГц.

а

б
Рис. 29. Распределения модулей амплитуд напряжений и токов на частоте 8.2 ГГц.
Кривые 1 и 2 соответствуют первой и второй гармоникам частоты. Как было показано в разделе 2 в ЭМК с указанными параметрами на частоте около 7.7 ГГц наблюдается пространственный синхронизм между основной волной на первой гармонике и высшим типом волны на второй гармонике.
Из рисунков,
представленных выше, видно, что распределение модулей напряжений и в
особенности токов на второй гармонике имеет нарастающий характер на частоте
7.69 ГГц. При этом напряжения на первой гармонике заметно уменьшаются с ростом ![]() . В этом сказывается
влияние пространственного синхронизма. На частоте 8.2 ГГц удаленной от частоты
синхронизма распределения модулей амплитуд напряжений и токов имеют
осциллирующий характер. При этом максимальные значения напряжений и токов
существенно уступают таким же их значениям на частоте 7.69 ГГц. Таким образом,
мы можем сделать вывод о том, что при нарушении условий пространственного
синхронизма интенсивность преобразования энергии первой гармоники во вторую
уменьшается.
. В этом сказывается
влияние пространственного синхронизма. На частоте 8.2 ГГц удаленной от частоты
синхронизма распределения модулей амплитуд напряжений и токов имеют
осциллирующий характер. При этом максимальные значения напряжений и токов
существенно уступают таким же их значениям на частоте 7.69 ГГц. Таким образом,
мы можем сделать вывод о том, что при нарушении условий пространственного
синхронизма интенсивность преобразования энергии первой гармоники во вторую
уменьшается.
Литература
1. Манцызов Б.И. Когерентная и нелинейная оптика фотонных кристаллов. М.: Физматлит. 2010.
2. Уизем Дж. Линейные и нелинейные волны. М.: Мир. 1977.
3. Сазонов В.П., Силин Р.А. Замедляющие системы. М.: Сов. Радио. 1966.
4. Банков С.Е. Полубесконечный нелинейный электромагнитный кристалл // Радиотехника и электроника. 2011. Т. 56. № 5. С. 1-11/
5. Банков С.Е. Модель нелинейного электромагнитного кристалла // Радиотехника и электроника. 2011. Т. 56. № 3. С. 261-274.
6. Маттей Д.Л., Янг Л., Джонс Е.М.Т. Фильтры СВЧ, согласующие цепи и цепи связи // М.: «Связь». 1971. Т.1.
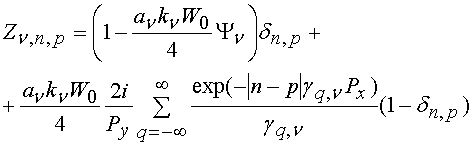 , (5)
, (5)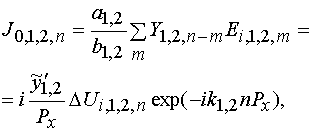 (24)
(24)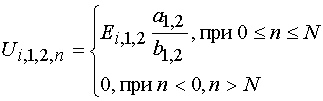 . (26)
. (26)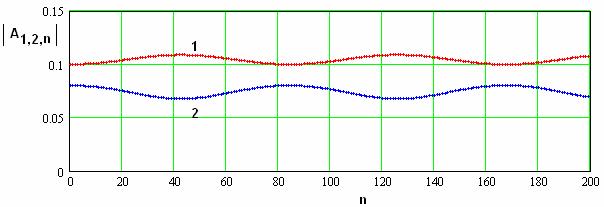
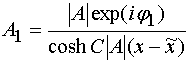 , (35)
, (35) ,
, 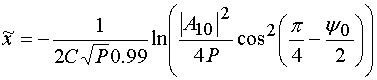 , (50)
, (50)