УДК 621.396
Согласованная фильтрация зашумленных дискретных кватернионных сигналов
Я. А. Фурман, И. Л. Егошина, Р. В. Ерусланов
Марийский государственный технический университет, г. Йошкар-Ола
Получена 12 марта 2012 г.
Аннотация. Получены основные аналитические соотношения для согласованной фильтрации дискретных кватернионных сигналов. Обнаружен эффект расщепления спектральных компонент фильтруемого сигнала. Исследован механизм формирования выходных сигналов при согласованной и несогласованной фильтрации таких сигналов. Рассмотрен пример различения изображений групповых точечных объектов по результатам согласованной фильтрации дискретных кватернионных сигналов.
Ключевые слова: дискретные комплекснозначные сигналы, дискретные кватернионные сигналы, групповые точечные объекты, различение пространственно расположенных точечных объектов, согласованная фильтрация, мера схожести сигналов, нормированное скалярное произведение.
Abstract. The main analytical relationships of matched filtration of discrete quaternion signals are obtained. The spectral component decomposition effect for filtered signal is disclosed. The mechanism of output signal forming at matched and non-matched filtration of these signals is investigated. The example of group point object images discriminating from matched filtration results of discrete quaternion signals are shown.
Keywords: discrete complex valued signal, discrete quaternion signal, uniform energy spectrum, ideal correlate properties, unitary vector space, quaternion vector space, elementary contour, composition contour, phase-coded signal processing, cyclic matched filtration, "by S-step incremental summing" algorithm.
Принятые сокращения: ГТО – групповой точечный объект, ИХ – импульсная характеристика, КЗС – комплекснозначный сигнал, КТС – кватернионный сигнал, КФ – кватернионный фильтр, НСП – нормированное скалярное произведение, СКО – среднеквадратическое отклонение, СП – скалярное произведение, СФ – согласованный фильтр, ЧКП – частотный коэффициент передачи, ЭВ – элементарный вектор, ЭК – элементарный контур, ЭКС – элементарный кватернионный сигнал.
1. Введение. Обоснование применимости кватернионных сигналов
Под дискретными КТС
будем понимать совокупность из s
4D векторов ![]() ,
каждый из которых задается одноименным полным кватернионом
,
каждый из которых задается одноименным полным кватернионом ![]() ,
, ![]() , где
, где ![]() – мнимые единицы, взаимодействующие по
следующим правилам [1,2,3]:
– мнимые единицы, взаимодействующие по
следующим правилам [1,2,3]:
![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() . (1)
. (1)
Если ![]() , то
кватернион
, то
кватернион ![]() называется векторным. С помощью подобных КТС
в 3D пространстве можно задать групповые
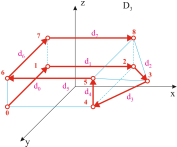
точечные объекты и изображения в виде многогранников (рис. 1) и на их основе
решать вопросы, связанные с различением и оценкой параметров такие объектов. Цель
данной работы состоит в исследовании механизма работы согласованных кватернионных
фильтров, вырабатывающих меру схожести двух КТС, необходимую для решения этих
задач в условиях действия шумов.
называется векторным. С помощью подобных КТС
в 3D пространстве можно задать групповые
точечные объекты и изображения в виде многогранников (рис. 1) и на их основе
решать вопросы, связанные с различением и оценкой параметров такие объектов. Цель
данной работы состоит в исследовании механизма работы согласованных кватернионных
фильтров, вырабатывающих меру схожести двух КТС, необходимую для решения этих
задач в условиях действия шумов.

Рис. 1. Задание трехмерной фигуры
пучком векторов ![]() .
.
Вещественные сигналы проигрывают КТС в том плане, что формируемая фильтром мера схожести ε двух сигналов, по величине которой принимается решение в задачах оценки параметров и различения 3D сигналов, более информативна при задании сигналов в кватернионном пространстве H. Скалярное произведение (СП) двух кватернионов включает в качестве своей составной части СП вещественных векторов, задаваемых этими кватернионами. Дополнительно оно содержит еще и гиперкомплексную часть в виде векторного произведения этих векторов, что дает возможность по выходному сигналу фильтра оценить параметры линейных преобразований фильтруемого сигнала. Данное обстоятельство позволяет выявить в кватернионном векторном пространстве более высокую, чем в действительном линейном пространстве R степень различия двух сигналов [3].
Например, пусть
совокупность векторных сигналов ![]() ,
, ![]() , образует с вектором сравниваемого
(эталонного) сигнала q
одинаковые углы
, образует с вектором сравниваемого
(эталонного) сигнала q
одинаковые углы ![]() . Сигналы
. Сигналы ![]() ,
, ![]() ,
представленные элементами линейного действительного пространства R,
характеризуются одинаковыми значениями нормированных СП
,
представленные элементами линейного действительного пространства R,
характеризуются одинаковыми значениями нормированных СП ![]() ,
,
![]() , и поэтому будут неразличимыми
относительно сигнала q.
Такую совокупность сигналов
, и поэтому будут неразличимыми
относительно сигнала q.
Такую совокупность сигналов ![]() ,
, ![]() , могут представлять собой образующие
конической поверхности, а направление оси конуса задается вектором q.
Если же сигналы
, могут представлять собой образующие
конической поверхности, а направление оси конуса задается вектором q.
Если же сигналы ![]() ,
, ![]() , и q
представить элементами кватернионного пространства H,
то различение сигналов
, и q
представить элементами кватернионного пространства H,
то различение сигналов ![]() ,
, ![]() ,
становится возможным благодаря дополнительным информативным признакам в виде
нормалей
,
становится возможным благодаря дополнительным информативным признакам в виде
нормалей ![]() к плоскостям, образованным парой векторов
к плоскостям, образованным парой векторов
![]() и q,
и q,
![]() . Этот признак вырабатывается при
вычислении СП
. Этот признак вырабатывается при
вычислении СП ![]() ,
, ![]() [5].
[5].
Отметим, что полный
кватернион в соответствии с процедурой Кэли-Диксона [6,3] вводится как удвоение
комплексного числа. Если, например, ![]() и
и ![]() – два комплексных числа, то в
соответствии с этой процедурой и правилами (1) кватернион z
будет
равен:
– два комплексных числа, то в
соответствии с этой процедурой и правилами (1) кватернион z
будет
равен:
![]() .
.
Следовательно,
обработка дискретного КТС может рассматриваться как обобщение обработки
дискретного комплекснозначного сигнала (КЗС) с учетом некоммутативности
операции перемножения мнимых единиц ![]() . Под дискретным КЗС
. Под дискретным КЗС
![]() понимается упорядоченная совокупность s
векторов
понимается упорядоченная совокупность s
векторов ![]() ,
, ![]() ,
задающих вершины расположенного в комплексной плоскости ориентированного
многоугольника (полигонального контура) [5].
,
задающих вершины расположенного в комплексной плоскости ориентированного
многоугольника (полигонального контура) [5].
С методической точки зрения анализ работы линейных фильтров, согласованных с дискретными КТС, целесообразно выполнить по аналогии с анализом работы фильтров для дискретных комплекснозначных и вещественных сигналов.
2. Дискретные комплекснозначные сигналы
Одномерный случай.
СП произведение векторов ![]() и
и ![]() , как элементов унитарного пространства
, как элементов унитарного пространства ![]() , вводится следующим образом [7]
, вводится следующим образом [7]
 . (2)
. (2)
Как следует из (2),
реальная часть этого произведения, равная ![]() , есть
СП векторов
, есть
СП векторов ![]() и
и ![]() в пространстве R2:
в пространстве R2:
![]() . Следовательно, СП векторов в унитарном
пространстве С в качестве своей составной части содержит СП этих же векторов в
пространстве R и за счет дополнительной
мнимой части
. Следовательно, СП векторов в унитарном
пространстве С в качестве своей составной части содержит СП этих же векторов в
пространстве R и за счет дополнительной
мнимой части ![]() обладает большей информативностью в отношении
исходных векторов [7]. Мнимая часть СП (2) задает ориентированную (с учетом
знака) площадь параллелограмма, построенного на векторах
обладает большей информативностью в отношении
исходных векторов [7]. Мнимая часть СП (2) задает ориентированную (с учетом
знака) площадь параллелограмма, построенного на векторах ![]() и
и ![]() :
: ![]() .
С учетом результат этого СП в тригонометрической форме имеет вид:
.
С учетом результат этого СП в тригонометрической форме имеет вид:
![]() ,
, ![]() . (3)
. (3)
Мера схожести
векторов ![]() и
и
![]() определяется величиной расстояния между
ними. Для нормированных
векторов
определяется величиной расстояния между
ними. Для нормированных
векторов ![]()
![]() и квадрат расстояния будет равен
и квадрат расстояния будет равен
![]() . (4)
. (4)
Как следует из
(2) и (4), в одномерном случае и мера схожести и косинус угла между
нормированными векторами являются одной и той же величиной ![]() . Этот результат совпадает со случаем
задания векторных сигналов в пространстве R.
. Этот результат совпадает со случаем
задания векторных сигналов в пространстве R.
Мера схожести
векторных сигналов в пространстве C1,
определяемая величиной ![]() ,
будет функцией двух переменных: схожести форм сигналов, задаваемых векторами
,
будет функцией двух переменных: схожести форм сигналов, задаваемых векторами ![]() и
и ![]() , и величиной угла φ между
ними. Угол φ является неконтролируемой величиной. Информативной для
принятия решения о сходстве сигналов величиной является схожесть их форм.
Поэтому величину ε целесообразно вычислять в случае, когда угол φ
равен нулю. Такие векторные сигналы будем называть согласованными по углу
поворота.
, и величиной угла φ между
ними. Угол φ является неконтролируемой величиной. Информативной для
принятия решения о сходстве сигналов величиной является схожесть их форм.
Поэтому величину ε целесообразно вычислять в случае, когда угол φ
равен нулю. Такие векторные сигналы будем называть согласованными по углу
поворота.
Многомерный случай. Пусть
![]() и
и ![]() –
два дискретно кодированных КЗС размерности s.
Векторы
–
два дискретно кодированных КЗС размерности s.
Векторы ![]() и
и ![]() далее
будем также называть парциальными компонентами КЗС Г и N,
а скалярное произведение
далее
будем также называть парциальными компонентами КЗС Г и N,
а скалярное произведение ![]() – парциальным СП этих
векторов,
– парциальным СП этих
векторов, ![]() . Данные СП равно [7]:
. Данные СП равно [7]:
 (5)
(5)
Перейдем к
нормированным КЗС ![]() и
и ![]() и
запишем выражение для их НСП
и
запишем выражение для их НСП
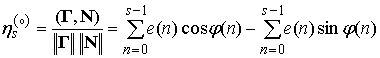 , (6)
, (6)
где
![]() .
.
Представим комплексное число (6) в тригонометрическом виде:
![]() . (7)
. (7)
Принимая во внимание (6), аргумент этого числа будет равен
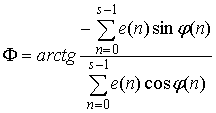 . (8)
. (8)
Если теперь
вектор Г повернуть на угол – Ф, то СП ![]() станет
вещественным числом, равным
станет
вещественным числом, равным ![]() . Отсюда следует, что
угол Ф, являясь аргументом СП (6), одновременно равен углу между сигналами Г
и N.
. Отсюда следует, что
угол Ф, являясь аргументом СП (6), одновременно равен углу между сигналами Г
и N.
Рассмотрим вопрос об определении меры схожести ε сигналов Г° и N°. Значение этой меры не должно зависеть от угла Ф между векторами Г° и N° и определяет лишь различие форм сигналов. Форма каждого из сигналов не меняется при их вращении, но поскольку это преобразование влияет на величину расстояния между сигналами, то величину ε следует вычислять при таком значении угла между сигналами, когда расстояние между ними становится минимальным. Тогда значение реальной части НСП будет равно значению этой меры:
![]() при
при ![]() . (9)
. (9)
Квадрат расстояния между сигналами Г° и N° с учетом (7) равен
![]() . (10)
. (10)
Повернем сигнал Г°
на угол (–Ф) и вычислим СП (7):![]() . В этом случае выражение
(10) примет вид
. В этом случае выражение
(10) примет вид ![]() . При фиксированных формах
сигналов Г и N
оно
задает минимальное расстояние между ними. Тогда в соответствии с (9) мера схожести
сигналов будет равна модулю НСП сигналов Г и N:
. При фиксированных формах
сигналов Г и N
оно
задает минимальное расстояние между ними. Тогда в соответствии с (9) мера схожести
сигналов будет равна модулю НСП сигналов Г и N:
![]() .
.
Таким образом, при задании нормированных КЗС в унитарном пространстве с размерностью s>1 значения угла Ф между векторами, задающими эти сигналы, и мера схожести ε сигналов по их форме будут равны:
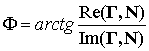 ;
; ![]() . (11)
. (11)
Если же угловое
согласование сигналов не выполнено, то ![]() . В последнем
выражении мера схожести ε учитывает не только схожесть форм сигналов, но и
величину угла Ф (разность их фаз) между ними. Сравним подходы к определению
меры схожести ε двух дискретно кодированных сигналов Г°
и N°,
представленных элементами пространств R
и C. В обоих случаях значение меры
. В последнем
выражении мера схожести ε учитывает не только схожесть форм сигналов, но и
величину угла Ф (разность их фаз) между ними. Сравним подходы к определению
меры схожести ε двух дискретно кодированных сигналов Г°
и N°,
представленных элементами пространств R
и C. В обоих случаях значение меры ![]() определяется в результате вычисления НСП
сигналов Г и N,
являющегося функцией двух переменных: 1) степени схожести форм данных сигналов
и 2) величины угла Ф между векторами («фазовым сдвигом»), задающими данные
сигналы. Нередко, например, в задачах различения сигналов, угол Ф служит
неинформативным параметром и его влияние на значение вычисляемой меры
определяется в результате вычисления НСП
сигналов Г и N,
являющегося функцией двух переменных: 1) степени схожести форм данных сигналов
и 2) величины угла Ф между векторами («фазовым сдвигом»), задающими данные
сигналы. Нередко, например, в задачах различения сигналов, угол Ф служит
неинформативным параметром и его влияние на значение вычисляемой меры ![]() стараются исключить. С этой целью
выполняется угловое согласование сигналов, в результате которого угол между
векторами становится равным нулю.
стараются исключить. С этой целью
выполняется угловое согласование сигналов, в результате которого угол между
векторами становится равным нулю.
При задании КЗС
в пространстве R величина
косинуса угла Ф одновременно является значением меры схожести ![]() сигналов и выполнить угловое согласование
сигналов по информации, содержащейся в НСП, невозможно. Вычисленное значение
меры схожести
сигналов и выполнить угловое согласование
сигналов по информации, содержащейся в НСП, невозможно. Вычисленное значение
меры схожести ![]() содержит систематическую
ошибку, вызванную зависимостью расстояния между сигналами от угла Ф.
содержит систематическую
ошибку, вызванную зависимостью расстояния между сигналами от угла Ф.
НСП сигналов Г
и N, представленных
элементами унитарного пространства ![]() , является более информативной
величиной по сравнению с НСП сигналов, заданных в пространстве R.
В результате перед вычислением меры схожести форм сигналов удается выполнить их
угловое согласование и затем найти значение
, является более информативной
величиной по сравнению с НСП сигналов, заданных в пространстве R.
В результате перед вычислением меры схожести форм сигналов удается выполнить их
угловое согласование и затем найти значение ![]() , характеризующее
меру схожести только форм сравниваемых сигналов. Однако основное
преимущество – представление сигналов в унитарном пространстве
, характеризующее
меру схожести только форм сравниваемых сигналов. Однако основное
преимущество – представление сигналов в унитарном пространстве ![]() , приводящее к инвариантности получаемого
значения меры схожести форм сигналов к углу между векторами, является важным
аргументом в пользу такого подхода.
, приводящее к инвариантности получаемого
значения меры схожести форм сигналов к углу между векторами, является важным
аргументом в пользу такого подхода.
Покажем
применение полученных результатов на примере решения задачи различения
дискретных комплекснозначных сигналов, представленных элементами унитарного
пространства. Задача различения КЗС ставится следующим образом. Задан алфавит
из М эталонных сигналов ![]() размерности s,
каждый из которых образует самостоятельный класс
размерности s,
каждый из которых образует самостоятельный класс ![]() ,
, ![]() . На входе системы различения подается КЗС
Г, полученный из эталонного сигнала
. На входе системы различения подается КЗС
Г, полученный из эталонного сигнала ![]() путем
изменения его масштаба
путем
изменения его масштаба ![]() , поворота на угол
, поворота на угол ![]() , сдвигом на величину d
номера начального вектора. Преобразованный сигнал
, сдвигом на величину d
номера начального вектора. Преобразованный сигнал ![]() складывается
с шумовым сигналом
складывается
с шумовым сигналом ![]() , компоненты которого является
отсчетами белого шума с нулевым математическим ожиданием и дисперсией
, компоненты которого является
отсчетами белого шума с нулевым математическим ожиданием и дисперсией ![]() :
:
![]() . (12)
. (12)
Здесь через ![]() обозначен векторный сигнал N,
нумерация компонент которого сдвинута на величину
обозначен векторный сигнал N,
нумерация компонент которого сдвинута на величину ![]() .
Параметры
.
Параметры ![]() ,
,![]() , d,
l сигнала Г считаются
неизвестными. Необходимо по результатам анализа зашумленного векторного сигнала
Г отнести его к одному из классов алфавита
, d,
l сигнала Г считаются
неизвестными. Необходимо по результатам анализа зашумленного векторного сигнала
Г отнести его к одному из классов алфавита ![]() .
.
Рассмотрим пример
различения дискретного КЗС по критерию максимума степени схожести. Алфавит
состоит из классов ![]() и содержит следующие
нормированные эталонные сигналы:
и содержит следующие
нормированные эталонные сигналы:
![]() ;
;
![]() ;
;
![]() .
.
Различаемый сигнал ![]() получен поворотом эталонного сигнала
получен поворотом эталонного сигнала ![]() на угол
на угол ![]() с
последующим зашумлением, а сдвиг его компонент по отношению к соответствующим
компонентам
с
последующим зашумлением, а сдвиг его компонент по отношению к соответствующим
компонентам ![]() отсутствует. Структура устройства различения
приведена на рис. 2. Она содержит 3 параллельно работающих канала, которые
формируют значения ε1,ε2 и ε3
мер
отсутствует. Структура устройства различения
приведена на рис. 2. Она содержит 3 параллельно работающих канала, которые
формируют значения ε1,ε2 и ε3
мер

Рис. 2. Структура устройства различения ДКС Г°.
схожести различаемого сигнала Г°
с эталонными сигналами ![]() ,
, ![]() и
и ![]() . Как видно из результатов работы узлов
устройства различения, максимальное значение меры схожести сигнала Г°
обнаружено с сигналом
. Как видно из результатов работы узлов
устройства различения, максимальное значение меры схожести сигнала Г°
обнаружено с сигналом ![]() : ε2=0,960. Поэтому
решающее устройство, работающее по критерию максимума меры схожести, принимается
решение о том, что различаемый сигнал относится к классу
: ε2=0,960. Поэтому
решающее устройство, работающее по критерию максимума меры схожести, принимается
решение о том, что различаемый сигнал относится к классу ![]() .
.
3. Основные положения линейной фильтрации КЗС
В пространстве ![]() , существует ортогональный базис
, существует ортогональный базис ![]() , где
, где ![]() –
элементарный контур (ЭК) порядка m,
равный
–
элементарный контур (ЭК) порядка m,
равный
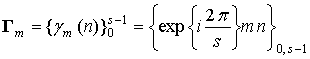 , (13)
, (13)
по которому разлагается произвольный дискретный КЗС Г:
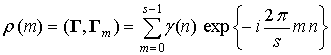 ,
, ![]() .
.
Спектр ![]() элементарного
контура
элементарного
контура ![]() состоит из одной ненулевой компоненты
состоит из одной ненулевой компоненты ![]() . Операция сопряжения ЭК снова приводит к
ЭК из того же семейства, но другого порядка:
. Операция сопряжения ЭК снова приводит к
ЭК из того же семейства, но другого порядка:
![]() ,
, ![]() ,
, ![]() ,
,
т.е. операция сопряжения не связана с
выходом ЭК ![]() из базиса.
из базиса.
Линейная фильтрация
дискретных КЗС ![]() , частным случаем которых служат
вещественные сигналы, представляет собой целенаправленный процесс изменения их
спектра путем умножения каждой их гармоники
, частным случаем которых служат
вещественные сигналы, представляет собой целенаправленный процесс изменения их
спектра путем умножения каждой их гармоники ![]() на
комплексное число
на
комплексное число ![]() , в результате чего она
изменяется по амплитуде в
, в результате чего она
изменяется по амплитуде в ![]() раз и получает
дополнительный фазовый сдвиг
раз и получает
дополнительный фазовый сдвиг
![]() ,
, ![]() . Дискретный КЗС
. Дискретный КЗС ![]() является частотным коэффициентом передачи
(ЧКП) фильтра, причем
является частотным коэффициентом передачи
(ЧКП) фильтра, причем
![]() ,
, ![]() . (14)
. (14)
Благодаря процедуре линейности в спектре выходного сигнала нет новых гармоник относительно спектра входного сигнала N (рис. 3). Данное обстоятельство объясняется тем, что монохроматический входной сигнал

Рис. 3. Сохранение монохроматической структуры спектра входного КЗС
при его линейной фильтрации.
![]() является
собственным вектором линейного оператора фильтрации и преобразуется без
искажения формы. При этом
является
собственным вектором линейного оператора фильтрации и преобразуется без
искажения формы. При этом ![]() – характеристическое число
оператора, задающее параметры линейного преобразования входного
монохроматического сигнала
– характеристическое число
оператора, задающее параметры линейного преобразования входного
монохроматического сигнала ![]() . Временное
пространственное преобразование КЗС N
при его линейной фильтрации является преобразованием свертки двух дискретных КЗС
. Временное
пространственное преобразование КЗС N
при его линейной фильтрации является преобразованием свертки двух дискретных КЗС
![]() и
и ![]() :
:
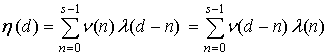 ,
, ![]() . (15)
. (15)
Дискретный КЗС ![]() называется импульсной характеристикой
(ИХ) фильтра и является реакцией фильтра на сигнал с равномерным спектром.
Подобным сигналом является кронекеровский сигнал
называется импульсной характеристикой
(ИХ) фильтра и является реакцией фильтра на сигнал с равномерным спектром.
Подобным сигналом является кронекеровский сигнал ![]() ,
имеющий спектр
,
имеющий спектр ![]() . При его фильтрации в
соответствии с (15) получим
. При его фильтрации в
соответствии с (15) получим
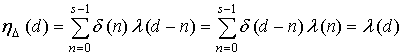 ,
, ![]() .
.
Приведенное соотношение
связывает сигналы ![]() и
и ![]() . Выходной
сигнал в виде
. Выходной
сигнал в виде ![]() получается, если входной сигнал
имеет спектр вида
получается, если входной сигнал
имеет спектр вида ![]() ,
, ![]() .
Тогда выражение (14) примет вид
.
Тогда выражение (14) примет вид ![]() , т.е. с точностью до
константы
, т.е. с точностью до
константы ![]() спектр выходного сигнала состоит из
компонент
спектр выходного сигнала состоит из
компонент ![]() ,
, ![]() .
Следовательно, ЧКП
.
Следовательно, ЧКП ![]() и ИХ
и ИХ ![]() линейного
дискретного фильтра с точностью до константы
линейного
дискретного фильтра с точностью до константы ![]() связаны
ДПФ:
связаны
ДПФ:
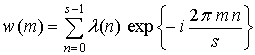 ,
, ![]() .
.
Далее выполним анализ, целью которого будет сравнение полученных характеристик линейного фильтра для фильтрации дискретных КЗС с аналогичными характеристиками фильтров для дискретных КТС.
4. Задание дискретных кватернионных сигналов
Для преобразований КТС зададим
в кватернионном пространстве ортогональный базис. На основании процедуры
Кели-Диксона такой базис может быть получен из базиса элементарных контуров
(ЭК) ![]() , образующих ортогональный базис в
унитарном пространстве
, образующих ортогональный базис в
унитарном пространстве ![]() [8,9]:
[8,9]:
![]()
![]() ,
, ![]() . (16)
. (16)
КТС ![]() ,
, ![]() ,
назовем элементарным кватернионным сигналом (ЭКС) порядка
,
назовем элементарным кватернионным сигналом (ЭКС) порядка ![]() . Скалярное произведение КТС
. Скалярное произведение КТС ![]() и
и ![]() имеет
вид [7,8]
имеет
вид [7,8]
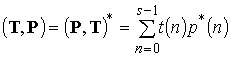 . (17)
. (17)
Здесь ![]() – сопряженный кватернион, причем
– сопряженный кватернион, причем ![]() – квадрат модуля кватерниона
– квадрат модуля кватерниона ![]() . Скалярный квадрат
. Скалярный квадрат 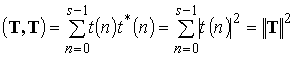 – называется квадратом нормы или энергией
КТС
– называется квадратом нормы или энергией
КТС ![]() . Отметим, что из-за некоммутативности операции
умножения кватернионный коэффициент
. Отметим, что из-за некоммутативности операции
умножения кватернионный коэффициент ![]() при одном из КТС можно
вынести за знак СП лишь в том случае, если он расположен слева, т.е.
при одном из КТС можно
вынести за знак СП лишь в том случае, если он расположен слева, т.е.
![]() ,
,
![]() , но
, но ![]() . (18)
. (18)
При действиях с
кватернионами используются вытекающие из правил (1) преобразования вида ![]() и
и ![]() , где
, где ![]() – комплексное число. ДПФ
– комплексное число. ДПФ
![]() кватернионного
сигнала
кватернионного
сигнала ![]() находится
как
находится
как ![]() , а
ОДПФ
, а
ОДПФ ![]() – как
скалярное произведение
– как
скалярное произведение ![]() [8]:
[8]:
 ,
, ![]() ;
;
(19)
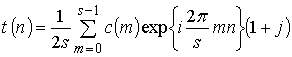 ,
, ![]() .
.
Также отметим, что
произвольный КТС ![]() , для
которого справедливы разложения (19), из-за периодичности функции
, для
которого справедливы разложения (19), из-за периодичности функции ![]() также обладает
периодом
также обладает
периодом ![]() , т.е.
, т.е. ![]() и, в частности,
и, в частности, ![]() .
.
Спектр ЭКС ![]() ,
, ![]() , с учетом (16) и (18)
равен
, с учетом (16) и (18)
равен
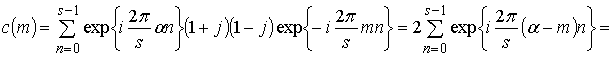
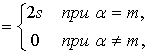
![]() . (20)
. (20)
5. Основные соотношения для кватернионных фильтров [9]
Процедуру фильтрации
дискретного КТС ![]() определим
в виде, аналогичном виду выражения (15)
определим
в виде, аналогичном виду выражения (15)
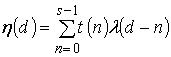 ,
, ![]() . (21)
. (21)
При таком определении
кватернионный фильтр (КФ) вырабатывает значения меры схожести между пучками
векторов ![]() и
и ![]() в условиях
варьировании параметра
в условиях
варьировании параметра ![]() и при следующем порядке перебора кватернионов
КТС
и при следующем порядке перебора кватернионов
КТС ![]() :
: ![]() . Подадим на вход КФ
сигнал
. Подадим на вход КФ
сигнал ![]() в виде
полного нормированного семейства ЭКС, т.е.
в виде
полного нормированного семейства ЭКС, т.е.
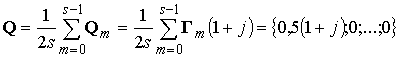 . (22)
. (22)
Данный сигнал имеет
равномерный спектр ![]() .
В результате выходной сигнал воспроизведет ИХ фильтра в виде КТС
.
В результате выходной сигнал воспроизведет ИХ фильтра в виде КТС ![]() с весом
с весом ![]() . Для выяснения
частотных свойств КФ рассмотрим процесс фильтрации ЭКС
. Для выяснения
частотных свойств КФ рассмотрим процесс фильтрации ЭКС ![]() ,
, ![]() , представляющего собой монохроматический
сигнал с ненулевой компонентой спектра
, представляющего собой монохроматический
сигнал с ненулевой компонентой спектра ![]() :
:
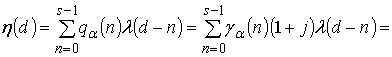
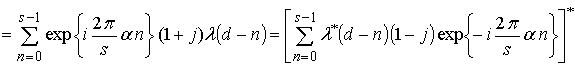 .
.
Последнее выражение
является результатом сопряженного ДПФ сигнала ![]() . Тогда
. Тогда
 ,
, ![]() , (23)
, (23)
где
![]() (24)
(24)
– компонента кватернионно-сопряженного спектра сигнала в виде ИХ КФ. Переходя от компонент сигналов к самим сигналам, получим
![]() . (25)
. (25)
Следовательно,
реакция КФ на сигнал в виде ЭКС ![]() равна произведению ЭК
равна произведению ЭК ![]() и кватерниона
и кватерниона ![]() ,
, ![]() . Определим спектр
сигнала (25):
. Определим спектр
сигнала (25):
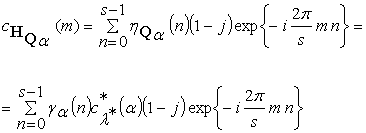 .
.
Хотя кватернионный
множитель ![]() и не
зависит от переменной суммирования
и не
зависит от переменной суммирования ![]() , но его нельзя без нарушения правил
умножения вынести за знак суммы. Поэтому для получения наглядных результатов
выходной сигнал (23) с учетом (24) представим в виде:
, но его нельзя без нарушения правил
умножения вынести за знак суммы. Поэтому для получения наглядных результатов
выходной сигнал (23) с учетом (24) представим в виде:
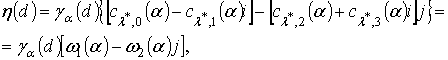 ,
(26)
,
(26)
где
![]() ,
, ![]() . (27)
. (27)
В результате
![]() .
.
С учетом того, что ![]() и элементарные
контуры
и элементарные
контуры ![]() и
и ![]() ,
, ![]() ,
, ![]() , взаимно ортогональны,
окончательно получим
, взаимно ортогональны,
окончательно получим
 (28)
(28)
Таким образом, КФ
реагирует на монохроматический сигнал расщеплением этой гармоники на две. Одна из них имеет исходное значение частоты ![]() , а другая – зеркальное значение
, а другая – зеркальное значение ![]() (рис. 4).
(рис. 4).

Рис. 4. Расщепление спектральной линии входного сигнала при прохождении через КФ.
Поскольку
гармоника входного сигнала
на частоте ![]() имеет
значение, равное
имеет
значение, равное ![]() , то,
как следует из (28) и (27), коэффициент ее передачи на исходной частоте
, то,
как следует из (28) и (27), коэффициент ее передачи на исходной частоте ![]() , равен
, равен
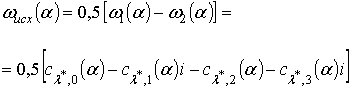 . (29)
. (29)
На
зеркальной частоте ![]() этот
коэффициент имеет вид
этот
коэффициент имеет вид
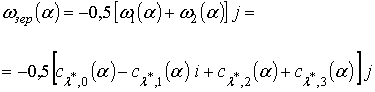 . (30)
. (30)
6. Фильтрация произвольного дискретного КТС
Пусть теперь на вход КФ
подается произвольный КТС ![]() . В соответствии с (21) фильтр
вырабатывает сигнал
. В соответствии с (21) фильтр
вырабатывает сигнал ![]() .
В каждом слагаемом выражения (21) отсчет
.
В каждом слагаемом выражения (21) отсчет ![]() заменим его спектральным разложением
заменим его спектральным разложением  ,
, ![]() . Здесь
. Здесь ![]() ,
, ![]() , – компонента спектра
входного КТС
, – компонента спектра
входного КТС ![]() . В
результате выражение (21) примет вид
. В
результате выражение (21) примет вид
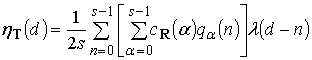 ,
, ![]() .
.
Используя выражения (26) и
(27), определяющие реакцию фильтра на ЭКС ![]() , получим
, получим
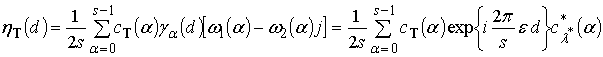 . (31)
. (31)
Для нахождения спектра выходного сигнала выполним ДПФ выражения (31):
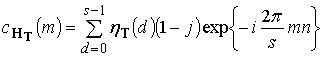 ,
, ![]() .
.
Подставив значение ![]() и изменив в
получившейся двойной сумме порядок суммирования, будем иметь:
и изменив в
получившейся двойной сумме порядок суммирования, будем иметь:
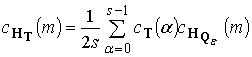 . (32)
. (32)
Как видно из (28), спектр
выходного сигнала КФ при фильтрации ЭКС ![]() содержит лишь две ненулевые компоненты.
Поэтому выражение (31) также будет состоять лишь из двух слагаемых, которые с
учетом (29) и (30) будут равны:
содержит лишь две ненулевые компоненты.
Поэтому выражение (31) также будет состоять лишь из двух слагаемых, которые с
учетом (29) и (30) будут равны:
![]() ,
, ![]() . (33)
. (33)
Следовательно, при
фильтрации произвольного КТС в образовании ![]() -ой гармоники спектра выходного сигнала
принимают участие
-ой гармоники спектра выходного сигнала
принимают участие ![]() -ая и
-ая и ![]() -ая гармоники входного
сигнала соответственно с коэффициентами передачи
-ая гармоники входного
сигнала соответственно с коэффициентами передачи ![]() и
и ![]() . Таким образом, КТС
. Таким образом, КТС ![]() частотного коэффициента
передачи КФ состоит из элементов
частотного коэффициента
передачи КФ состоит из элементов ![]() , каждый из которых представляет собой
двухкомпонентный вектор
, каждый из которых представляет собой
двухкомпонентный вектор ![]() ,
, ![]() . Первая компонента является коэффициентом
передачи по частоте исходной гармоники, а второй – по частоте зеркальной
гармоники (рис. 5).
. Первая компонента является коэффициентом
передачи по частоте исходной гармоники, а второй – по частоте зеркальной
гармоники (рис. 5).
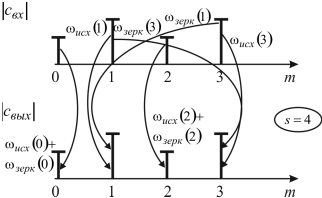
Рис. 5. Влияние спектра входного сигнала КФ на образование гармоник спектра входного сигнала (s=4).
Рассмотрим теперь характер
связи между частотным коэффициентом передачи ![]() фильтра и его ИХ. Предварительно отметим,
что
фильтра и его ИХ. Предварительно отметим,
что ![]() -ая
гармоника сигнала в виде ИХ кватернионного фильтра формируется при подаче на
его вход сигнала
-ая
гармоника сигнала в виде ИХ кватернионного фильтра формируется при подаче на
его вход сигнала ![]() ,
представляющего собой нормированную сумму двух компонент
,
представляющего собой нормированную сумму двух компонент ![]() . Тогда в соответствии
с выражениями (22) и (33)
. Тогда в соответствии
с выражениями (22) и (33) ![]() -ая гармоника спектра сигнала в виде ИХ
фильтра будет равна
-ая гармоника спектра сигнала в виде ИХ
фильтра будет равна
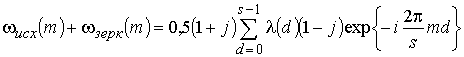 ,
, ![]() . (34)
. (34)
Таким образом, ИХ и
частотный коэффициент передачи КФ, также как и аналогичные характеристики
обычных фильтров, связаны между собой ДПФ, но с учетом векторной структуры
компоненты ![]() .
.
7. О собственных элементах кватернионного фильтра
Собственными элементами
кватернионного оператора ![]() назовем вектор
назовем вектор ![]() с кватернионными компонентами
с кватернионными компонентами ![]() и кватернион
и кватернион ![]() , удовлетворяющие соотношению
, удовлетворяющие соотношению
![]() . Видно, что оператор
. Видно, что оператор ![]() сохраняет вид кватернионного
вектора
сохраняет вид кватернионного
вектора ![]() с
точностью до масштабного коэффициента
с
точностью до масштабного коэффициента ![]() . В рассматриваемом случае роль оператора
. В рассматриваемом случае роль оператора ![]() выполняет КФ с
импульсной характеристикой
выполняет КФ с
импульсной характеристикой ![]() .
.
При спектральном анализе
вещественных сигналов широко применяется их представление в виде двух
комплексных сигналов: ![]() . Аналогичное соотношение имеет место для
комплексного сигнала
. Аналогичное соотношение имеет место для
комплексного сигнала ![]() в
виде разности двух ЭКС:
в
виде разности двух ЭКС:
![]() ,
, ![]() . (35)
. (35)
На основании (25)
результат фильтрации заданного в кватернионном пространстве ЭК ![]() ,
, ![]() , будет равен
, будет равен
![]() . (36)
. (36)
Отсюда видно, что реакцией
КФ на сигнал в виде ЭК ![]() служит тот же ЭК
служит тот же ЭК ![]() , умноженный на кватернион
, умноженный на кватернион ![]() ,
, ![]() . Таким образом,
. Таким образом, ![]() и
и ![]() ,
, ![]() , являются собственными
элементами КФ. Как видно из (36), собственный сигнал
, являются собственными
элементами КФ. Как видно из (36), собственный сигнал ![]() в виде элементарного контура порядка
в виде элементарного контура порядка ![]() , заданный в кватернионном
пространстве, воспроизводится на выходе КФ в виде двух ЭКС
, заданный в кватернионном
пространстве, воспроизводится на выходе КФ в виде двух ЭКС ![]() и
и ![]() порядков
порядков ![]() и
и ![]() . Поэтому собственный
сигнал КФ будет, в отличии от собственных сигналов вещественных и
комплекснозначных фильтров, уже не монохроматическим, а состоящим из двух
спектральных компонент на частотах
. Поэтому собственный
сигнал КФ будет, в отличии от собственных сигналов вещественных и
комплекснозначных фильтров, уже не монохроматическим, а состоящим из двух
спектральных компонент на частотах ![]() и
и ![]() .
.
При подаче на вход КФ
монохроматического сигнала в виде ЭКС ![]() выходной сигнал задается выражением (25).
Используя соотношение (35) получим
выходной сигнал задается выражением (25).
Используя соотношение (35) получим
![]() . (37)
. (37)
Отсюда видно, что КФ
расщепляет гармонику входного сигнала на частоте ![]() на две гармоники с частотами
на две гармоники с частотами ![]() и
и ![]() . Такое искажение КФ
входного сигнала с монохроматическим спектром является следствием того, что ЭКС
. Такое искажение КФ
входного сигнала с монохроматическим спектром является следствием того, что ЭКС
![]() не является
собственным сигналом кватернионного фильтра.
не является
собственным сигналом кватернионного фильтра.
8. Согласованная фильтрация дискретных КТС
Согласованные фильтры
играют важную роль при решении основных задач обработки зашумленных сигналов.
Принятие решения об обнаружении или различения таких сигналов производится по
величине меры схожести с эталонным сигналом, которая вырабатывается
согласованным фильтром. Выходной сигнал КФ, согласованного с КТС ![]() , при фильтрации произвольного КТС
, при фильтрации произвольного КТС ![]() определяется выражением [8,9]
определяется выражением [8,9]
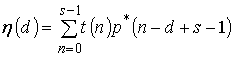 ,
,
![]() . (38)
. (38)
Определим частотную и
импульсную характеристики кватернионного согласованного фильтра. С этой целью
предварительно рассмотрим прохождение через такой фильтр ЭКС ![]() ,
, ![]() . С
учетом (38) выражение (23) для рассматриваемого случая принимает вид
. С
учетом (38) выражение (23) для рассматриваемого случая принимает вид
 .
.
Здесь ![]() – сопряженный спектр сигнала
– сопряженный спектр сигнала ![]() , с которым согласован фильтр. При
, с которым согласован фильтр. При ![]() выходной сигнал становится равным
соответствующей кватернионно-сопряженной компоненте спектра сигнала
выходной сигнал становится равным
соответствующей кватернионно-сопряженной компоненте спектра сигнала ![]() , т.е.
, т.е. ![]() .
Фазовый множитель
.
Фазовый множитель ![]() в этом случае компенсирует
фазовый сдвиг входного сигнала
в этом случае компенсирует
фазовый сдвиг входного сигнала ![]() , равный
, равный ![]() . Спектр выходного сигнала описывается выражением
(28), но с учетом того, что
. Спектр выходного сигнала описывается выражением
(28), но с учетом того, что
![]() ,
,
![]() .
(39)
.
(39)
Отсюда следует, что
коэффициент передачи согласованного фильтра ЭКС ![]() равен
на исходной частоте
равен
на исходной частоте
 ,
,
на зеркальной частоте
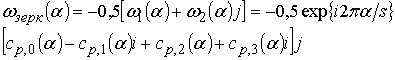 ,
,
При фильтрации
согласованного КТС ![]() выходной сигнал фильтра в соответствии
с (31) и (39) имеет вид
выходной сигнал фильтра в соответствии
с (31) и (39) имеет вид
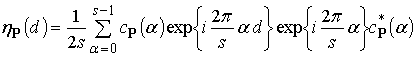 .
.
Спектр этого сигнала определяется выражением (33):
![]() ,
,
![]() .
.
При ![]() формируется пиковый выходной сигнал,
равный энергии сигнала
формируется пиковый выходной сигнал,
равный энергии сигнала ![]() :
:
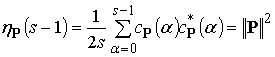 .
.
Импульсная
характеристика фильтра с учетом нормирующего коэффициента, полученная как
реакция фильтра на сигнал 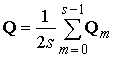 , равна
, равна ![]() . Ее связь с компонентами ЧКП
. Ее связь с компонентами ЧКП ![]() определяется выражением (34)
определяется выражением (34)
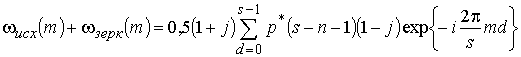 .
.
9. Комплексная форма кватернионного согласованного фильтра
В п.1. было отмечено, что процедура Кэли-Диксона позволяет рассматривать кватернион как удвоенное комплексное число и, соответственно, КТС – как удвоенный комплексный сигнал. С этой позиции работу согласованного КФ можно проанализировать как обобщение работы согласованного фильтра (контурного согласованного фильтра) дискретных КЗС. Если
![]() и
и
![]() – (40)
– (40)
два комплексных сигнала, то текущий выходной отсчет контурного фильтра, согласованного с КЗС U, имеет вид
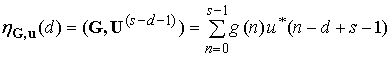 , (41)
, (41)
где ![]() –
КЗС со смещенным на s-d-1
начальной компонентой,
–
КЗС со смещенным на s-d-1
начальной компонентой, ![]() . На рис. 6
представлены векторные диаграммы, поясняющие механизм работы контурного
фильтра, согласованного с сигналом
. На рис. 6
представлены векторные диаграммы, поясняющие механизм работы контурного
фильтра, согласованного с сигналом ![]() в виде контура
треугольника, при образовании пикового отсчета.
в виде контура
треугольника, при образовании пикового отсчета.
|
а) |
|
|
б) |
в) |
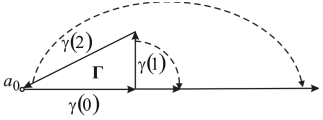
Рис.
6. Механизм работы контурного согласованного фильтра для комплекснозначных сигналов:
а) контур треугольника ![]() и
повороты его векторов при обнулении их аргументов; б) квадрирование по длине
повернутых векторов контура; в) образование выходного сигнала при суммировании
преобразованных векторов входного сигнала.
и
повороты его векторов при обнулении их аргументов; б) квадрирование по длине
повернутых векторов контура; в) образование выходного сигнала при суммировании
преобразованных векторов входного сигнала.
КТС представляется суммой, в состав которой входят два комплекснозначных сигнала. Учитывая правила действия с линейными единицами (1), согласованный фильтр для КТС представлен в виде композиции двух согласованных фильтров для КЗС. Зададим КТС Q и P в комплексной форме:
![]()
![]()
Скалярное произведение двух КТС, выраженное через СП составляющих их комплексных слагаемых, равно
![]() . (42)
. (42)
Поскольку ![]() и
и ![]() , то в
соответствии с (40) и (41) согласованный фильтр с КТС P
должен выполнять операцию
, то в
соответствии с (40) и (41) согласованный фильтр с КТС P
должен выполнять операцию
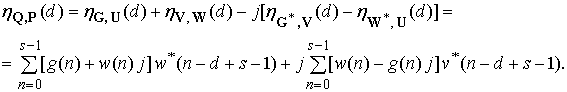 (43)
(43)
Отсюда следует, что
кватернионный СФ представляет совокупность двух комплекснозначных фильтров.
Один из них согласован с КЗС W,
а другой – с КЗС V, причем первый
из них фильтрует КТС Q,
а второй – Qj.
При ![]() выходной отсчет фильтра
выходной отсчет фильтра

представляет собой СП КТС. Если же фильтруется сигнал, с которым фильтр согласован, т.е. если
![]() ;
; ![]() ;
; ![]() ,
,
то выходной сигнал фильтра становится чисто вещественным и равным энергии фильтруемого сигнала:
 .
.
10. Механизм работы кватернионного согласованного фильтра [8].
Анализ работы
кватернионного СФ выполним, опираясь на механизм работы СФ для
комплекснозначных сигналов ![]() . Для проведения
анализа кватернионного СФ кватернионом
. Для проведения
анализа кватернионного СФ кватернионом ![]() представим
в комплексной форме:
представим
в комплексной форме: ![]() . Аналогично зададим и весь КТС
. Аналогично зададим и весь КТС ![]() :
:
![]() ;
; ![]() ;
; ![]() .
.
При таком
представлении СФ для нормированного и согласованного с ним сигнала, задается
суммой комплексной ![]() и гиперкомплексной
и гиперкомплексной ![]() части:
части:
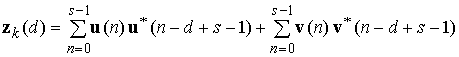 ,
,
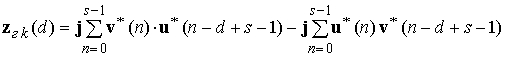 ,
d=0,1,…,s-1.
,
d=0,1,…,s-1.
Из этих соотношений, следует что кватернионный СФ представляет собой совокупность параллельно работающих комплексного и гиперкомплексного звеньев (рис 7):
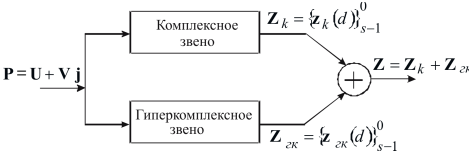
Рис.7 Структура кватернионного фильтра.
Первое звено состоит из параллельно работающих контурных фильтров, результаты которых суммируются. Один из них согласован с контуром U, а второй – с контуром V. Второе звено, гиперкомплексное, работает, с комплекснозначными сигналами V и U, подверженными действию оператора j. Оба фильтра работают в несогласованных режимах, что вызвано подачей на вход каждого из них сигнала, не совпадающего с эталонным. Выходной сигнал звена определяется разностью выходных сигналов первого и второго фильтров. При d=s-1 они становятся одинаковыми и компенсируют друг друга. В результате выходной сигнал кватернионного СФ определяется только первым, комплексным, звеном.
Таким образом,
механизм работы кватернионного СФ при фильтрации согласованного с ним сигнала P=U+V
заключается в образовании при d=s-1
вещественного пикового отсчета, равного энергии входного КТС, т.е. равного ![]() . Это достигается согласованной работой в
режиме синфазного накопления, выполняемого контурными фильтрами первого
(комплексного) звена СФ. Второе (гиперкомплексное) звено СФ в этот момент
образует нулевой сигнал, получающийся благодаря синхронному вычитанию
одинаковых сигналов с выходов двух фильтров, работающих в несогласованных
режимах (рис. 8). При несогласованной фильтрации КТС
. Это достигается согласованной работой в
режиме синфазного накопления, выполняемого контурными фильтрами первого
(комплексного) звена СФ. Второе (гиперкомплексное) звено СФ в этот момент
образует нулевой сигнал, получающийся благодаря синхронному вычитанию
одинаковых сигналов с выходов двух фильтров, работающих в несогласованных
режимах (рис. 8). При несогласованной фильтрации КТС
a)

b) 
c) 
Рис. 8. Механизм работы кватернионного согласованного фильтра: а)
согласованный с фильтром КТС ![]() ;
; ![]() ;
; ![]() ; б) формирование сигнала на выходе комплексного звена
при
; б) формирование сигнала на выходе комплексного звена
при
![]() ; в) формирование
сигнала
; в) формирование
сигнала
c)на выходе
гиперкомплексного звена при ![]() .
.
равенство этих вычитаемых сигналов не выполняется и выходной сигнал всего фильтра теряет вещественный характер.
11.Примеры.
11.1.Различение векторных сигналов, заданных на боковой поверхности конуса
На рис. 9 представлены пять векторов, заданных кватернионами:
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ,
,
Векторы
расположены на боковой поверхности конуса с осью OZ
и совпадают с его образующими. Эти же векторы, заданные в пространстве ![]() , имеют вид:
, имеют вид:
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
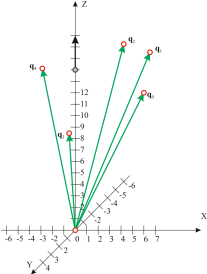
Рис. 9. Заданные на боковой поверхности
конуса векторы ![]() ,
, ![]() .
.
Задача заключается в
различении каждого из пяти векторных сигналов относительно векторного сигнала ![]() , являющегося направляющим вектором оси OZ
конуса. Различение векторных сигналов возможно в том случае, если мера схожести
, являющегося направляющим вектором оси OZ
конуса. Различение векторных сигналов возможно в том случае, если мера схожести
![]() вектора
вектора ![]() с
векторами
с
векторами ![]() , n=0,1,2,3,4,
будет различной для каждого значения n.
Значение меры схожести
, n=0,1,2,3,4,
будет различной для каждого значения n.
Значение меры схожести ![]() для векторов
для векторов ![]() , заданных в пространстве
, заданных в пространстве ![]() , одно и тоже:
, одно и тоже: ![]() , n=0,1,2,3,4.
Следовательно, векторы не различимы относительно вектора
, n=0,1,2,3,4.
Следовательно, векторы не различимы относительно вектора ![]() . Такой результат объясняется тем, что
угол между любой образующей конуса и его осью, один и тот же.
. Такой результат объясняется тем, что
угол между любой образующей конуса и его осью, один и тот же.
Ниже приведены значения
НСП, полученные в пространстве H1
и заданные кватернионами в тригонометрической форме ![]() ,
, ![]() . Здесь Ф – угол между векторами q
и ρ, а r
– нормаль к собственной плоскости, образованной этими векторами:
. Здесь Ф – угол между векторами q
и ρ, а r
– нормаль к собственной плоскости, образованной этими векторами:
![]() ;
; ![]()
![]() ;
; ![]() ;
;
![]() ;
; ![]()
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
В данном случае
различение векторов ![]() , n=0,1,2,3,4,
становится возможным благодаря тому, что нормали
, n=0,1,2,3,4,
становится возможным благодаря тому, что нормали ![]() к
собственным плоскостям существенно отличаются друг от друга.
к
собственным плоскостям существенно отличаются друг от друга.
Рассмотренный пример
носит достаточно искусственный характер. Но на практике часто встречаются
ситуации, особенно в условиях действия шумов, когда меры схожести ![]() нескольких векторных сигналов с эталонным
сигналом, представленные в пространстве R,
незначительно отличаются друг от руга. В этих условиях дополнительный информативный
призрак, получаемый при переходе в пространстве H,
существенно повышает вероятность принятия правильного решения.
нескольких векторных сигналов с эталонным
сигналом, представленные в пространстве R,
незначительно отличаются друг от руга. В этих условиях дополнительный информативный
призрак, получаемый при переходе в пространстве H,
существенно повышает вероятность принятия правильного решения.
11.2. Различение изображений многогранных тел с использованием согласованных кватернионных фильтров
|
|
|
|
|
а) |
б) |
в) |
Рис.10.
Эталонные многогранники: а) класса ![]() , б) класса
А1,
в) класса А2 .
, б) класса
А1,
в) класса А2 .
Различаемый
многогранник (МГР) ![]() необходимо отнести к од ному из классов
необходимо отнести к од ному из классов ![]() ,
каждый из которых задан эталонным МГР
,
каждый из которых задан эталонным МГР ![]() ,
, ![]() (рис.10).Все МГР имеют одинаковую
размерность
(рис.10).Все МГР имеют одинаковую
размерность ![]() и заданы координатами своих вершин. Последовательность
номеров вершин каждого из МГР упорядочена в соответствии с методикой,
приведенной в работе [11]. Математической моделью МГР служит 3D
полигональный замкнутый контур
и заданы координатами своих вершин. Последовательность
номеров вершин каждого из МГР упорядочена в соответствии с методикой,
приведенной в работе [11]. Математической моделью МГР служит 3D
полигональный замкнутый контур ![]() размерностью
размерностью ![]() , элементарные векторы которого заданы
кватернионами и единственным образом проходят через все вершины МГР.
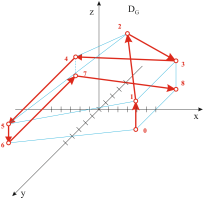
Формирование подобных проволочных моделей МГР рассмотрено в [11]. Изображение
таких моделей для каждого из эталонных МГР приведены на рис. 11.
, элементарные векторы которого заданы
кватернионами и единственным образом проходят через все вершины МГР.
Формирование подобных проволочных моделей МГР рассмотрено в [11]. Изображение
таких моделей для каждого из эталонных МГР приведены на рис. 11.
|
|
|
|
|
а) |
б) |
в) |
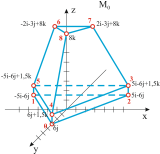
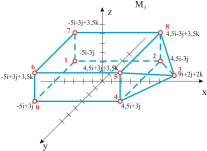
Рис. 11. Проволочные модели эталонных многогранников:
а) класса ![]() ,
б) класса А1, в) класса А2.
,
б) класса А1, в) класса А2.
В аналитическом виде эти модели представляются следующим образом:
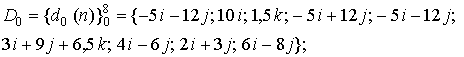
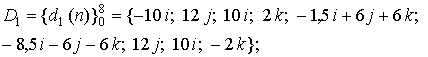
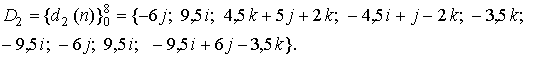
Различаемый МГР ![]() (рис.12) получен поворотом эталонного МГР
М1 вокруг оси OZ
на
угол
(рис.12) получен поворотом эталонного МГР
М1 вокруг оси OZ
на
угол ![]() , сдвигом начала его номеров вершин на
, сдвигом начала его номеров вершин на ![]() номера и аддитивно искажен шумовым МГР
номера и аддитивно искажен шумовым МГР ![]() :
:
![]() , (44)
, (44)
где через ![]() обозначен
МГР М1 со сдвинутыми на 3 единицы номерами своих вершин.
обозначен
МГР М1 со сдвинутыми на 3 единицы номерами своих вершин.
|
|
|
|
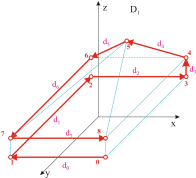
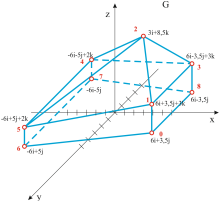
Рис. 12. Различаемый МГР G.
|
Рис. 13. Проволочная модель различаемого МГР G. |
На рис. 13 представлена проволочная
модель ![]() различаемого МГР G,
а ниже приведено ее аналитическое представление:
различаемого МГР G,
а ниже приведено ее аналитическое представление:
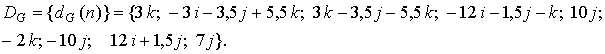
Параметры преобразования эталонного МГР
М1 в различаемый МГР G
и сам номер эталонного МГР считаются неизвестными. Структура устройства различения
3D сигнала в виде МГР G
является многоканальной по числу классов. В каждом канале вычисляется мера
схожести ![]() ,
, ![]() ,
различаемого и эталонного МГР одного из классов (рис. 14).
,
различаемого и эталонного МГР одного из классов (рис. 14).
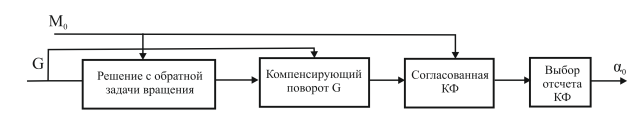
Рис. 14. Структура канала формирования меры схожести различаемого G и эталонного МГР М0.
Оценка параметров поворота МГР G получается в результате решения обратной задачи вращения МГР [12,13]. Ее надо решить в первую очередь, так как согласование номеров парциальных компонент проволочной модели МГР G с компонентами проволочных моделей эталонных МГР возможно только после углового согласования МГР.
При повороте МГР вокруг
оси с направляющим вектором ![]() на угол
на угол ![]() подобным преобразованиям подвергаются все
парциальные компоненты его проволочной модели. На этом свойстве основан метод
решения обратной задачи, описанный в [13]. Решение выполняется в два этапа –
находится вектор
подобным преобразованиям подвергаются все
парциальные компоненты его проволочной модели. На этом свойстве основан метод
решения обратной задачи, описанный в [13]. Решение выполняется в два этапа –
находится вектор ![]() оси
поворота, а затем вычисляется угол
оси
поворота, а затем вычисляется угол ![]() .
.
Отметим, что решение обратной задачи будет корректным лишь в том случае, если определяются параметры вращения различаемого МГР G относительно МГР М1, преобразованием которого он был получен. Но поскольку такая информация отсутствует, то процедуру необходимо проводить в отношении эталонных МГР всех классов алфавита.
Для некорректной задачи
можно ограничиться лишь первым этапом ее решения, т.е. определением вектора ![]() . Для такой задачи дисперсия оценок вектора
. Для такой задачи дисперсия оценок вектора
![]() для каждой парциальной пары кватернионов
из проволочных моделей двух МГР – G
и Dm,
для каждой парциальной пары кватернионов
из проволочных моделей двух МГР – G
и Dm,
![]() , будет значительно превышать дисперсию
оценки вектора
, будет значительно превышать дисперсию
оценки вектора ![]() при решении корректной задачи.
На этом основании второй этап обратной задачи, связанный с оценкой угла
поворота
при решении корректной задачи.
На этом основании второй этап обратной задачи, связанный с оценкой угла
поворота ![]() , решается для случая, когда дисперсия
углов направления задаваемых парциальными осями вращения, будет достаточно
низкой.
, решается для случая, когда дисперсия
углов направления задаваемых парциальными осями вращения, будет достаточно
низкой.
Применительно к
рассматриваемому примеру СКО угла отклонения вектора ![]() относительно
его среднего значения для класса A0
равно 29,9°, для класса A1
равно 0,9° и для класса A2
– 12,6° –. Если принять пороговое значение СКО на уровне
относительно
его среднего значения для класса A0
равно 29,9°, для класса A1
равно 0,9° и для класса A2
– 12,6° –. Если принять пороговое значение СКО на уровне ![]() , то на основании приведенных данных можно
считать, что различаемый МГР был получен поворотом эталонного МГР М1 вокруг оси
, то на основании приведенных данных можно
считать, что различаемый МГР был получен поворотом эталонного МГР М1 вокруг оси
![]() на угол
на угол ![]() . В
результате компенсирующего поворота на угол
. В
результате компенсирующего поворота на угол ![]() вокруг
оси OZ получим
модифицированную проволочную модель
вокруг
оси OZ получим
модифицированную проволочную модель ![]() различаемого МГР G,
согласованную с эталонным МГР М1 по угловым параметрам.
различаемого МГР G,
согласованную с эталонным МГР М1 по угловым параметрам.

Далее в соответствии со
структурной схемой на рис. 14 выполняется фильтрация проволочной модели ![]() различаемого МГР тремя фильтрами, согласованными
с проволочными моделями D0,D1,D2
эталонных МГР M0,M1
и M2.
различаемого МГР тремя фильтрами, согласованными
с проволочными моделями D0,D1,D2
эталонных МГР M0,M1
и M2.
Ниже приведены результаты в виде реальных частей пронормированных выходных отсчетов фильтров.
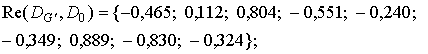
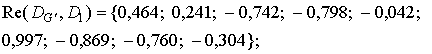
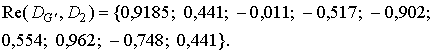
Пиковые отсчеты
фильтров для каждого из трех классов соответственно равны: ![]() ;
; ![]() ;
; ![]() . Значения этих отсчетов характеризуют
меру схожести различаемого МГР с каждым из классов алфавита. Если решение о
классе различаемого объекта G
принимать по максимуму меры схожести
. Значения этих отсчетов характеризуют
меру схожести различаемого МГР с каждым из классов алфавита. Если решение о
классе различаемого объекта G
принимать по максимуму меры схожести ![]() , то объект G
следует отнести к классу A1.
, то объект G
следует отнести к классу A1.
По результатам
согласованной фильтрации с помощью соотношения ![]() , где
, где ![]() – номер пикового отсчета в выходном КТС
фильтра, можно оценить параметр d
смещения начал нумерации элементов проволочных моделей МГР
– номер пикового отсчета в выходном КТС
фильтра, можно оценить параметр d
смещения начал нумерации элементов проволочных моделей МГР ![]() и М1. В нашем случае
и М1. В нашем случае ![]() , поэтому нумерация вершин различаемого
МГРG сдвинута на
, поэтому нумерация вершин различаемого
МГРG сдвинута на ![]() относительно нумерации вершин эталонного
объекта М1.
относительно нумерации вершин эталонного
объекта М1.
Таким образом,
различаемый объект G относится к
классу ![]() . Он повернут на
. Он повернут на ![]() вокруг
оси OZ относительно
эталонного объекта М1, а нумерация его вершин сдвинута на
вокруг
оси OZ относительно
эталонного объекта М1, а нумерация его вершин сдвинута на ![]() единицы.
единицы.
Рассмотренная в данном примере ситуация имеет отношение к задаче различения и оценке параметров пространственно расположенных групповых точечных объектов (ГТО). Как показано в работе [11], такому ГТО можно поставить в соответствие систему вложенных выпуклых МГР, что дает возможности упорядочить устойчивую математическую модель объекта, решить вопросы, связанные с его распознаванием (различением) и оценкой параметров, а также осуществить структурный анализ ГТО.
Заключение.
Расщепление текущей m-й
компоненты спектра входного сигнала на исходную с частотой m
и зеркальную с частотой s-m
является отличительной особенностью КФ по сравнению с фильтрами для
вещественных и комплекснозначных сигналов. При этом принцип суперпозиции для КФ
сохраняется, т.е. если ![]() и
и ![]() -
соответственно его реакции на сигналы
-
соответственно его реакции на сигналы ![]() и
и ![]() , то
, то ![]() .
Такое поведение фильтра обусловлено некоммутативностью операции умножения для
кватернионов. Например, вычислим скалярное произведение ЭК
.
Такое поведение фильтра обусловлено некоммутативностью операции умножения для
кватернионов. Например, вычислим скалярное произведение ЭК ![]() и ЭКС
и ЭКС ![]() :
:
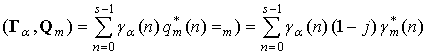 .
.
Если бы операция
умножения была бы коммутативной, то член![]() можно
было бы вынести за знак суммы и тогда
можно
было бы вынести за знак суммы и тогда
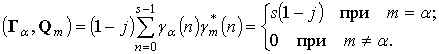
В результате расщепление
спектра не имело бы места. Невозможность такого преобразования для кватернионов
приводит к необходимости вычисления, в данном случае, не одного СП ![]() , а двух СП
, а двух СП ![]() и
и ![]() , имеющих ненулевые значения соответственно
на частотах
, имеющих ненулевые значения соответственно
на частотах ![]() и
и ![]() .
.
Эффект расщепления
гармоники входного сигнала на исходную и зеркальную вызван следующим отличием
КТС от комплекснозначных сигналов. Если ![]() ,
, 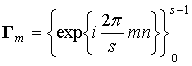 - ортогональный базис в унитарном пространстве
- ортогональный базис в унитарном пространстве
![]() , то ЭК
, то ЭК  есть
элемент этого базиса, равный
есть
элемент этого базиса, равный ![]() [5]. Поэтому линейная
фильтрация как сигнала
[5]. Поэтому линейная
фильтрация как сигнала ![]() , так и сигнала
, так и сигнала ![]() , характеризуется монохроматичностью
выходных сигналов, т.е. и
, характеризуется монохроматичностью
выходных сигналов, т.е. и ![]() и
и ![]() - это собственные векторы оператора
фильтрации.
- это собственные векторы оператора
фильтрации.
Если же ![]() ,
, 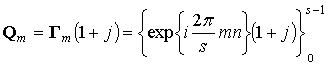 -
ортогональный базис в кватернионном пространстве, то операция сопряжения
становится причиной выхода КТС
-
ортогональный базис в кватернионном пространстве, то операция сопряжения
становится причиной выхода КТС ![]() за пределы базиса,
т.е. если
за пределы базиса,
т.е. если ![]() при
при ![]() , то
, то ![]() . В связи с этим операция кватернионного
сопряжения, выполняемая в процессе фильтрации, приводит к появлению зеркальной
частотной компоненты, отсутствующей во входном сигнале. В результате частотный
коэффициент фильтра, носит не скалярный, а векторный характер. Компоненты этого
вектора
. В связи с этим операция кватернионного
сопряжения, выполняемая в процессе фильтрации, приводит к появлению зеркальной
частотной компоненты, отсутствующей во входном сигнале. В результате частотный
коэффициент фильтра, носит не скалярный, а векторный характер. Компоненты этого
вектора ![]() и
и ![]() определяют
реакцию фильтра на гармонику входного сигнала с частотой
определяют
реакцию фильтра на гармонику входного сигнала с частотой ![]() , вызывающую отклик на частотах
, вызывающую отклик на частотах ![]() и
и ![]() .
.
Литература
1. Математическая энциклопедия т.2. М.: Советская энциклопедия. 1979. С.838.
2. Арнольд В.И. Геометрия комплексных чисел, кватернионов и спинов – М.: МЦНМО. 2002.
3. Кантор И.А., Солодовников А.С. Гиперкомплексные числа. М.: Наука, 1973.
4. Фурман Я.А., Егошина И.Л., Ерусланов Р.В. Согласованная фильтрация зашумленных дискретных кватернионных сигналов / Труды V Всероссийской конференции «Радиолокация и радиосвязь». Институт радиотехники и радиоэлектроники им. В.А. Котельникова РАН, 21-25 ноября 2011г. С. 292-297.
5. Введение в контурный анализ и его приложения к обработке изображений и сигналов: /Я.А. Фурман, А.В. Кревецкий, А.К. Передреев, А.А. Роженцов, Р.Г. Хафизов, И.Л. Егошина, А.Н. Леухин; -2-е изд., испр.-М.: ФИЗМАТЛИТ, 2003.-592 с.
6. Математическая энциклопедия т.3. М.: Советская энциклопедия. 1982. С.160.
7. Ефимов Н.В., Розендорн Э.Р. Линейная алгебра и многомерная геометрия. М.: Наука. 1974.
8. Furman Y.A. /Pattern Recognition and Image Analysis, 2002, v.12, №2б P.175.
9. Комплекснозначные и гиперкомплексные системы в задачах обработки многомерных сигналов / Я.А. Фурман, А.В. Кревецкий, А.А. Роженцов, Р.Г. Хафизов, А.Н. Леухин, И.Л. Егошина; Под. ред. Я.А. Фурмана. – М.: ФИЗМАТЛИТ , 2004. – 456.с.
10. Фурман Я.А., Хафизов Р.Г. Роженцов А.А., Фильтрация кватернионных сигналов // Радиотехника и электроника. 2007. Т. 52. №1. С. 1-9.
11. Фурман Я.А., Рябинин К.Б., Красильников М.И. Проволочная модель пространственного группового точечного объекта / Автометрия – 2008, Т. 44. №3. С. 3-16.
12. Фурман Я.А., Рябинин К.Б. Нахождение параметров вращения пространственного группового точечного объекта по результатам его фильтрации // Радиотехника и электроника. 2008. Т. 53. №1. С. 86-97.
13. Furman Y.A., Egoshina I.L. Inverse Problem of Rotation of Three-Dimensional Vector Signals / Optoelectronics instrumentation and data processing c/c of avtometriia. 2010. Vol. 46, No. 1, 37-46.