Восстановление одномерных финитных сигналов, прошедших через фильтр низких частот
А. Ю. Зражевский, В. А. Коротков
ИРЭ им. В.А. Котельникова РАН, Фрязинский филиал
Получена 21 марта 2013 г.
Аннотация. В работе рассмотрена возможность восстановления одномерных финитных сигналов, прошедших через фильтр низких частот. Показано, что возможно полное восстановление исходного сигнала при условии ограниченности длительности сигнала.
Ключевые слова: восстановление сигналов, фильтр низких частот, преобразование Фурье.
Abstract. The possibility of restoring of one-dimensional finite signals passed through the low pass filter is considered. It is shown an ability to recover the original signal provided that the signal is time limited.
Keywords: signal restoration, low-pass filter, Fourier transform.
Существуют методы, которые сводятся к восстановлению исходного сигнала по сигналу, прошедшему через идеальный фильтр низких частот (ФНЧ). В общем виде эта задача представляется неразрешимой. Однако, если входной сигнал ограничен по времени или пространству, то решение возможно [1-3]. В данной работе, в отличие от представленных ранее, рассматривается способ на основе получения ограниченного по частоте спектра из известного сигнала.
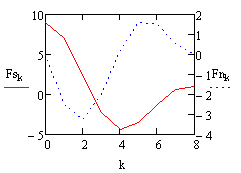
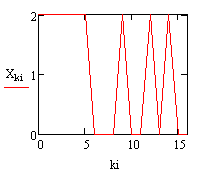
Пусть сигналы на выходе ФНЧ и на входе ФНЧ имеют вид:
|
|
|
|
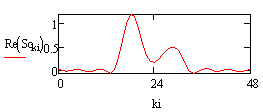
Рис.1.Сигнал на выходе ФНЧ. |
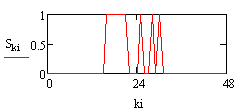
Рис.2.Сигнал на входе ФНЧ. |
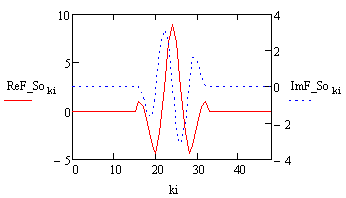
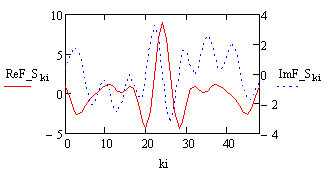
График на Рис.2 был получен из сигнала, который дополнили с обеих сторон нулями. Далее был рассчитан спектр этого сигнала, спектр ограничили и с помощью обратного преобразования Фурье получили график на Рис.1. Спектры выходного из ФНЧ и входного сигнала представлены на рисунках 3 и 4 соответственно.
|
|
|
|
Рис.3.Спектр сигнал на выходе ФНЧ. |
Рис.4.Спектр сигнал на входе ФНЧ. |
Для расчета спектра сигнала на входе ФНЧ используем формулу:
 , (1)
, (1)
где f( j ) – входной сигнал,
F(k) – спектр «входного» сигнала, N+1 – количество отсчетов входного сигнала. Так как спектр
выходного сигнала ограничен полосой пропускания ФНЧ, то k меняется от ![]() до
до
![]() и
и ![]() . В
силу того, что нас интересует не весь входной сигнал, а только его ненулевая
часть, можно пределы суммирования в (1) брать меньше. Выражение (1) можно
представить в виде системы линейных уравнений или умножения матриц:
. В
силу того, что нас интересует не весь входной сигнал, а только его ненулевая
часть, можно пределы суммирования в (1) брать меньше. Выражение (1) можно
представить в виде системы линейных уравнений или умножения матриц:
![]() . (2)
. (2)
Решение (2) относительно f – исходного сигнала наталкивается на некоторые трудности, связанные с комплексным характером матриц A и F и линейной зависимостью уравнений, связанную в первую очередь с симметрией A и F. Поэтому целесообразно разделить A, f и F на симметричные и антисимметричные части и решать полученные уравнения раздельно. Далее из симметричной и антисимметричной части построить полное решение. Поступая так, получим :
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
В дальнейшем учтем, что в (3)-(5) k меняется от 0 до ![]() , а j меняется от 0 до ненулевого
исходного сигнала, что в прочем не критично. Уравнения (2) теперь выглядят так:
, а j меняется от 0 до ненулевого
исходного сигнала, что в прочем не критично. Уравнения (2) теперь выглядят так:
![]() (6)
(6)
Решение переопределенных уравнений (6) проводим методом SVD [4]. Графики симметричной и антисимметричной частей F представлены на рис.5. Полученное решение после суммирования симметричной и антисимметричной частей находится на рис.6.
|
|
|
|
Рис.5.Части спектра на выходе ФНЧ. |
Рис.6. Полученное решение. (без нулевых частей, ограничивающих |
Сравнение Рис.6 и Рис.2. позволяет сделать вывод о полном восстановлении входного сигнала. Отметим, что ключевым моментом успешного восстановления сигнала является знание ограниченности входного сигнала по времени или пространству.
1. М.А.Броварова, С.Н.Хонина. Повышение разрешающей способности с помощью вытянутых сфероидальных волновых функций. Компьютерная оптика, 21, 53-57, 2001.
2. К.М.Ермохин. Технология построения разрезов методом аналитического продолжения геофизических полей. Геоинформатика, 2, 51-60, 2010.
3. Л.А.Айзенберг, Б.А.Кравцов. Вычислительный эксперимент по сверхразрешению физических приборов в экстраполяции спектра Фурье одномерных финитных сигналов. Письма в ЖТФ. 13. №9. 1987.
4. Дж. Форсайт, М. Малькольм, К. Моулер - Машинные методы математических вычислений. «Мир». 1980.