УДК 004.043,004.62
МЕТОД ОЦЕНКИ ЭФФЕКТИВНОСТИ РЕАЛИЗАЦИИ БЛОЧНОГО АЛГОРИТМА НА ОСНОВЕ ГРАФИЧЕСКОГО ПРОЦЕССОРА В ОТКРЫТОЙ ГЕТЕРОГЕННОЙ СИСТЕМЕ
Е. Г. Андрианова, Д. И. Мирзоян, А. Б. Петров
Московский государственный технический университет радиотехники, электроники и автоматики" (МГТУ МИРЭА)
Статья получена 20 марта 2014 г.
Аннотация. При построении высокопроизводительных систем большое внимание уделяется оптимизации реализаций. Открытые гетерогенные системы обладают высокими показателями эффективности в определенном спектре задач. Некоторые задачи из этого спектра не имеют принятых методик оптимизации и модификации, например, блочные алгоритмы обработки данных. При этом создание метода математической оценки эффективности реализации представляется важным шагом в создании подобной методике, и особенно средств автоматической оптимизации, реализующих подобную методику.
Ключевые слова: открытые гетерогенные системы, математическая оценка эффективности реализации, автоматическая оптимизация, алгоритмы блочной обработки.
Abstract: Much attention is paid to optimizing the implementation when building high-performance systems. Open heterogeneous systems are providing high levels of efficiency in a certain range of applications. Some tasks from that range do not have any approved methods for optimization and modification, i.e. tasks of block symbolic data processing. Proofing the procedure of implementation’s efficiency estimation looks like a very significant step to build such methods. This procedure is the most important thing when building automated or automatic optimization instruments implementing such methods.
Key words: open heterogeneous systems, mathematical evaluation of the effectiveness of implementation, automated or automatic optimization instruments implement, block symbolic data processing.
Введение
При оптимизации или модификации фрагмента программы под определенную аппаратную архитектуру возникает проблема ограничения производительности реализации алгоритма особенностями целевой архитектуры открытой гетерогенной системы. Эта проблема особенно актуальна при применении специальных вычислительных устройств, таких как графические процессоры, сигнальные процессоры, программируемые логические интегральные схемы, проблемно-ориентированные процессоры. Во всех перечисленных случаях имеются известные архитектурные и аппаратные особенности, существенным образом влияющие на производительность выполняемого кода. Для смягчения этих особенностей, в случаях, когда они существенно влияют на конкретную реализацию, применяют различные методы модификации, такие как преобразование структур данных, эквивалентные преобразования алгоритмов, высокоуровневую и низкоуровневую оптимизации.
При модификации и оптимизации под конкретную архитектуру необходимо учитывать не только аппаратные особенности открытой гетерогенной системы, но и программные особенности - алгоритм, типичное его поведение, использование структур данных, частные случаи (наилучший и наихудший сценарии). Кроме того, для открытой гетерогенной системы особенно важно сохранить совместимость форматов данных с другими системами [1]. Обычно, при проведении мероприятий по модификации реализации алгоритма, эти особенности эмпирически учитываются специалистом, проводящим адаптацию. Для применения же автоматических и автоматизированных средств адаптации необходимы методы математической оценки эффективности того или иного варианта реализации. Эти методы должны учитывать особенности, как аппаратной платформы, так и модифицируемого алгоритма.
Открытые гетерогенные системы в этом плане представляются одним из основных плацдармов применения различных вариантов реализаций параллельных алгоритмов, методик адаптации и оптимизации. Открытые гетерогенные системы обладают широким спектром архитектурных особенностей, многие из которых нетривиально влияют на производительность реализации. Соответственно, возникает задача формализации и автоматизации подобных методик. Поскольку спектр задач, эффективно решаемых открытой гетерогенной системой, ограничен, то возможно создание средств, учитывающих основные особенности конкретной системы и некоторого основного класса задач. В современных открытых гетерогенных системах на базе графических процессоров этот класс задач давно известен - это задачи с большим количеством элементов данных, со сложной, но линейной вещественной обработкой. Средства оптимизации кода для таких задач в настоящее время включены в драйверы вычислительных устройств (графических процессоров) во все среды выполнения гетерогенных приложений. Это позволило существенно повысить степень интероперабельности высокопроизводительных открытых гетерогенных систем [2, 3].
Реализация блочных алгоритмов в открытых гетерогенных системах на базе графического процессора
Учитывая, что открытые гетерогенные системы обладают очень высокой эффективностью (вычислительной и экономической), возникает соблазн их применения и в других типах параллельных расчетных задач. Одной из таких областей является применение блочных алгоритмов, которые удовлетворяют самым основным ограничивающим критериям открытых гетерогенных систем на базе графического процессора — а именно, являются параллельной по данным задачей с большим объемом обрабатываемой информации, естественно, при соответственно большом объеме исходной задачи. В принципе любой алгоритм может быть применен для небольшой задачи, но применение высокопроизводительной системы, особенно открытой гетерогенной, в данном случае представляется нецелесообразным. Как показывает практика, при определенных усилиях, затраченных на модификацию реализации, достигнутая производительность может быть достаточно высока.
На эффективность применения того или иного алгоритма блочной обработки данных в первую очередь влияют особенности архитектуры открытой гетерогенной вычислительной системы на базе графического процессора [4]:
1. Высокая параллельность по данным, а не по коду.
2. Структуризация и особенности работы различных типов памяти графического процессора.
3. Малый объем «быстрой» памяти, доступной одному вычислительному потоку.
4. Специфика обработки логических выражений.
5. Специфика обработки условных переходов и циклов.
Высокая параллельность по данным, а не по коду. Данная особенность выражается в невозможности для графического процессора обрабатывать все обозначенное множество потоков выполнения независимо друг от друга. Все обрабатываемые мультипроцессором потоки должны находиться на одной ступени исполнения, хотя и могут обрабатывать при этом различные данные. Понятно, что именно эта особенность является основным ограничивающим фактором для решаемого гетерогенной системой спектра задач.
Структуризация и особенности работы различных типов памяти графического процессора. Графический процессор, по сравнению с универсальным, имеет существенно больше различных типов памяти, некоторые из которых обладают при этом нетривиальными свойствами. В отличие от универсального процессора, располагающего с точки зрения приложения двумя типами памяти (регистрами и оперативной) в графическом процессоре их четыре, каждый из которых обладает своими особенностями при использовании. При этом неверный выбор типа памяти или некорректное его использование приводит к весьма существенной потере производительности.
Хотя архитектура и способ доступа к наибольшему по объему типу памяти (глобальной) сходны с таковой у центрального процессора, графические процессоры (кроме отдельных представителей последних поколений графических процессоров) не имеют сложной многоуровневой системы кеширования данных. Это выливается не только в большие задержки при доступе к глобальной памяти, но и в дополнительную зависимость этих задержек, а самое главное, зависимость пропускной способности памяти от характера доступа к ней, т.е. от формата хранения данных.
Малый объем «быстрой» памяти, доступной одному вычислительному потоку. Фактически, ввиду отсутствия сложной структурированной кэш-памяти у графических процессоров (за исключением последнего поколения), каждому потоку выполнения доступен только один вид «быстрой» памяти — это регистры. Очевидно, что размер этой памяти крайне невелик, кроме того, эта память делится между выполняемыми на данном одиночном процессоре потоками, входящими в состав основы. Другие типы памяти имеют большие задержки при использовании и свои особенности архитектуры. Скажем, локальная память разделяется между всеми потоками основы на данном мультипроцессоре, память констант доступна только для чтения, глобальная память имеет колоссальные задержки при использовании. Таким образом, от правильного выбора типа памяти и корректной работы с ней производительность алгоритма зависит существенным образом.
Специфика обработки логических выражений. В современных графических процессорах результат логического выражения записывается в специальный предикатный регистр, аналогично многим универсальным процессорам с архитектурой VLIW (некоторые графические процессоры также построены на базе этой архитектуры). При ветвлении происходит полное вычисление всех веток ветвления, и в зависимости от значения предикатного регистра сохраняется тот или иной результат. Соответственно, результат вычисления других веток ветвления отбрасывается. Вообще, логические выражения используются в вычислениях с использованием графических процессоров довольно редко, в основном, в силу преобладания математических операций, независимых от входных данных.
Специфика обработки условных переходов и циклов. Как уже сказано выше, для вычисления
ветвлений используются предикатные регистры. Цикл же можно рассматривать как
множество ветвлений (с 1 исполняемой веткой), причем количество ветвлений равно
количеству итераций цикла. В случае графического процессора это означает, что
тело цикла будет выполнено наибольшее из всех возможных количество раз всеми
потоками (результаты лишних итераций будут отброшены), что в случае сильного
разброса количества повторов приводит к существенному падению
производительности. В случае вложенных циклов ситуация становится еще хуже, и
падение производительности в наихудших сценариях может достигать ![]() , где c — количество вложенных циклов, Ni — максимальное количество
итераций i-го цикла.
, где c — количество вложенных циклов, Ni — максимальное количество
итераций i-го цикла.
В общем случае, эти особенности нетривиально влияют на производительность алгоритма, особенно сложного, содержащего заметное количество циклов и условных переходов. При этом вложенные циклы, особенно с большим расхождением по количеству итераций (имеется ввиду большое число вариантов, а не абсолютная разница в количестве) влияют намного сильнее даже большого количества условий.
Соответственно приведенным архитектурным особенностям, выделим параметры реализации блочного алгоритма, которые в сочетании с этими особенностями оказывают наибольшее влияние на производительность алгоритма:
1. Характер использования памяти.
2. Характер структуры исходных данных.
3. Характер структуры выходных данных.
4. Объем необходимой временной памяти.
5. Характер цикличности (количество / вложенность / число итераций циклов).
6. Характер ветвлений (количество / вложенность).
Параметры выше перечислены в порядке убывания влияния на производительность системы. Показано, что характер использования памяти (последовательные/случайные обращения) является основным фактором, ограничивающим эффективность высокопроизводительных систем. Разница между наилучшим и наихудшим сценарием может достигать десятков тысяч раз, в зависимости от состава системы, реализации, объема данных. Нетрудно заметить, что параметры 2 и 3 являются производными от 1, однако были выделены в отдельные, поскольку на них разработчик реализации может влиять существенным образом (влияние разработчика на параметр 1 очень ограничено, этот параметр зависит в основном от характера алгоритма обработки данных).
Влияние параметра 4 на производительность существенно зависит от конкретной аппаратной реализации — наблюдается тенденция к увеличению размера регистровых файлов в современных графических процессорах. При этом данный параметр обладает некоторым пороговым значением — до определенной величины (равной объему регистрового файла, деленому на минимальное количество потоков на один процессор) его влияние заметно, но не катастрофично. При превышении этого порога в качестве временной памяти начинает использоваться глобальная, обладающая большими задержками, и производительность реализации катастрофически падает. Влияние 4 и 5 параметра рассмотрено в описании соответствующих аппаратных особенностей.
Все эти параметры могут быть оценены количественно. Введем нормализованную оценку каждого параметра как Ki, где i — номер параметра. Возьмем диапазон возможных значений оценки как (0; 1]. Поскольку каждый из параметров существенно влияет на производительность, в качестве оценочной возьмем мультипликативную функцию:
где Rн — результирующая нормализованная оценка эффективности реализации;
n — количество параметров реализации, на основе которых вычисляется оценка, в данном случае 6;
Ki — нормализованная оценка i-го параметра;
ωi — вес i-го параметра.
Очевидно, что диапазон итоговой оценки (0; 1]. Важно отметить, что итоговая оценка эффективности реализации является относительной, и может показать только сравнительный результат эффективности модификации, но ничего не говорит об абсолютной производительности реализации алгоритма.
Важно отметить, что при очень низких значениях оценок отдельных параметров результат оценки становится неверным. Не все параметры алгоритма и соответствующие им архитектурные особенности являются физически независимыми, и поэтому очень неэффективная деталь реализации может «спрятать» эффект потери производительности от менее неэффективной детали, в случае если потеря производительности от этих деталях базируется на одной и той же или смежных архитектурных особенностях.
В качестве весов отдельных параметров возьмем эмпирические оценки, показанные на рис. 1. Конкретные значения весовых коэффициентов должны вычисляться на основании практического анализа влияния отдельных особенностей гетерогенной системы в сочетании с соответствующими параметрами реализации алгоритма на итоговую производительность. Такой анализ можно провести путем создания некоторого набора образцовых реализаций, обладающих известными значениями параметров. При замерах производительности всех реализаций из данного набора можно вычислить степень влияния на производительность каждого параметра реализации, характерную для данной гетерогенной системы.
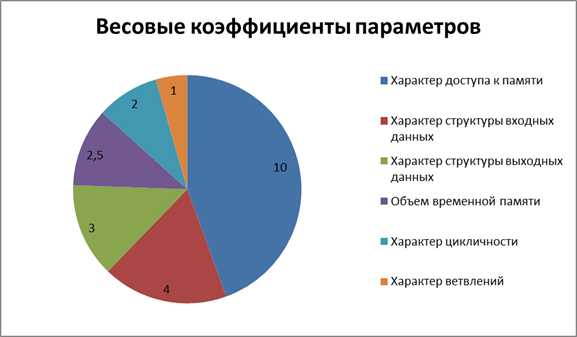
Рис.1. Весовые коэффициенты параметров реализации алгоритма.
Рассмотрим отдельные параметры реализации алгоритма и составим соответствующие оценочные функции для каждого из параметров.
Для параметра 1 — Характера доступа к памяти — в работе [5] установлено, что наибольшее влияние на производительность любой современной вычислительной системы оказывает характер доступа к памяти. Это проистекает из архитектурных особенностей современных вычислительных систем — имеется многоуровневая система памяти с различным объемом и задержками (кэш-память), построенная в соответствии с принципом локальности вычислительного процесса. В случае несоблюдения этого свойства локальности производительность и эффективность использования вычислительной системы падает катастрофическим образом.
Таким образом, возьмем в качестве оценки характера доступа к памяти следующую:
где LN — нормализованная оценка локальности обращений к памяти в диапазоне (0; 1]. 1 соответствует абсолютно локализованному доступу (доступу к одной и той же ячейке, или последовательному к группе ячеек), а 0 — абсолютно случайному доступу.
Одной из вторичных архитектурных особенностей некоторых современных вычислительных систем, и в частности, графических процессоров, являются независимые очереди запросов на чтение и запись в глобальную память. В таком случае следует разделить характер чтения и характер записи в память:
где LNR — нормализованная оценка локальности обращений по чтению, а LNW — нормализованная оценка локальности обращений по записи.
Более подробно проблемы локальности данных в гетерогенных системах на базе графических процессоров описаны в [6].
Следующий параметр, характер структуры входных данных, имеет непосредственное отношение к первому параметру, а также такой особенности современных графических процессоров, что чтение данных из памяти происходит строками, часто большими по размеру, чем отдельный элемент данных блочного алгоритма. Здесь часто применяют такие технологии, как совмещение и чередование данных [7]. Основная цель — добиться того, чтобы каждому мультипроцессору на очередной итерации обработки доставался блок данных соответствующий целому количеству строк. При этом важно, чтобы размер запрашиваемых данных не был слишком велик, так как это приведет к перегрузке подсистемы памяти [8], и кроме того, требует большого размера временной памяти (ухудшение параметра 4).
Следовательно, составим формулу оценки:
где SC — размер фрагмента данных одного потока,
NT — число потоков на одном мультипроцессоре,
NP — число процессоров в составе мультипроцессора,
SR — размер одной строки памяти.
Однако, данная оценка не является нормализованной. Она тем лучше, чем ближе P к целому числу. Кроме того, в случае, если P больше 1, итоговая эффективность тем выше, чем больше P. Если рассматривать разницу между P и следующим целым, можно считать ее накладными расходами (которыми она на самом деле и является), которые тем относительно меньше, чем P больше. Следовательно, составим нормализованную оценку:
где P — результат вычисления (4),
ceil(x) — округление x до ближайшего целого в большую сторону,
floor(x) — округление x до ближайшего целого в меньшую сторону.
Оценка для структуры выходных данных будет выглядеть точно также, за исключением другого весового коэффициента в формуле (1).
Объем быстрой временной памяти, доступной вычислительному блоку в составе графического процессора, очень невелик. При этом, этот объем делится на количество потоков, выполняемых на данном вычислительном блоке (размер основы). В случае нехватки размера регистрового файла, недостающая память будет выделена из состава глобальной памяти, памяти с большими задержками доступа, оказывая катастрофическое влияние на производительность.
где SRF — размер регистрового файла вычислительного блока графического процессора,
SD — размер временной памяти, необходимой реализации алгоритма
W — выбранный размер основы графического процессора (количество потоков на один вычислительный блок, минимальное значение у современных графических процессоров — 4).
Здесь важно отметить, что по формуле (6) значение коэффициента может превысить 1. В этом случае следует приравнять его к 1 — неиспользованная память не скажется положительно на эффективности реализации. Для устранения подобного неэффективного использования ресурсов вычислительной системы можно увеличить размер основы.
Циклы и условные переходы являются для графических
процессоров крайне нетипичным сценарием использования. И, в отличие от
нелокальности данных или большого объема временных данных, большинство
алгоритмов обработки данных использует в той или иной мере циклы и ветвления.
Из описания особенностей архитектуры графического процессора мы знаем, что в
случае, если в точке происходит дивергенция пути выполнения, то будут выполнены
все ветки алгоритма. В случае циклов это особенно важно, и является критичным
для вложенных циклов. Действительно, если подсчитать количество возможных
вариантов при вложенных циклах, то получим ![]() .
.
На основании этого составим оценку:
![]() , (7)
, (7)
где n — количество вложенных циклов,
c — количество возможных вариантов количества итераций,
Pi,j — вероятность наличия в i-м цикле j-го количества итераций,
Xi — Наиболее вероятное количество итераций i-го цикла,
Ii,j — j-й вариант количества итераций i-го цикла.
Из формулы (7) видно, что наиболее оптимальным вариантом будет наличие фиксированного количества итераций на любом уровне вложенности цикла.
Простые ветвления влияют на производительность намного меньше, чем циклы, особенно вложенные. Фактически, если затраты на расчет различных веток имеют один порядок, то влияние любого количества веток линейно. При этом наличие у оператора ветвления только одной ветки еще уменьшает влияние, т.к. потоки, не попадающие внутрь условной ветки, маскируются, ветка вычисляется, а когерентность потоков по факту не страдает. Таким образом:
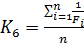 , (8)
, (8)
где n — количество операторов ветвления,
Fi — количество веток, причем вырожденные операторы ветвления (содержащие только одну ветку) считаются за 1.
По факту, ветвления часто оказывают даже положительное влияние на производительность — с их помощью можно избежать загрузки из памяти или записи в память ненужных значений, снизив тем самым нагрузку на подсистему памяти, которая оказывает наибольшее влияние на производительность [5, 6, 7]. Более подробно вопросы количества временной памяти, циклов и ветвлений и их влияние на практическую реализацию описаны в [9].
Заключение. При проведении мероприятий по модификации и оптимизации
реализаций алгоритмов важно объективно оценивать эффективность и прирост
производительности от предпринимаемых действий. При этом объективное
тестирование измененной реализации не всегда возможно — из за сложности
вычисления, большого объема задачи или несоответствия характеристик и
особенностей реальных и тестовых данных. Тем более такое объективное измерение
невозможно в случаях автоматической и автоматизированной оптимизации. Для этих
случаев целесообразно применять ту или иную методику математической или
экспертной оценки эффективности полученной реализации. В данной работе
предложен метод математической оценки эффективности реализации блочных
алгоритмов для графического процессора. Как и любая другая, предложенная
методика обладает своими преимуществами и недостатками. В частности, она имеет
очень много вариабельных параметров, причем таких, значения которых можно
получить только в результате экспериментов с использованием целевой
гетерогенной системы. В то же время, такие параметры позволяют гибко
подстраивать методику под весь спектр имеющихся на рынке и будущих аппаратных
решений в области гетерогенных вычислений. Также методика не может применяться
для сравнения производительности различных по своей сути алгоритмов — она дает
только некоторую оценку эффективности использования вычислительных ресурсов, и
не может применяться для оценки абсолютной производительности реализации
алгоритма. Также она не учитывает взаимосвязь некоторых параметров и
архитектурных особенностей между собой, особенно в области низких значений
эффективности. Тем не менее, ее можно применять при автоматизации модификации алгоритмов
для определения целесообразности применения тех или иных преобразований
алгоритма или структур данных.
Литература
1. Олейников А.Я. Технология открытых систем. // [Электронный ресурс]. URL: http://www.intuit.ru/studies/courses/1160/280/info
2. Ю.В. Гуляев, Е.Е. Журавлев, А.Я. Олейников Методология стандартизации для обеспечения интероперабельности информационных систем широкого класса. Аналитический обзор. // Журнал радиоэлектроникми: электронный журнал. 2012. №3. URL: http://jre.cplire.ru/jre/mar12/2/text.html
3. Е.Е. Журавлев, С.В. Иванов, А.А. Каменщиков, А.Я. Олейников, Е.И. Разинкин, К.А. Рубан. Интероперабельность в облачных вычислениях. // Журнал радиоэлектроникми: электронный журнал. 2013. №9. URL: http://jre.cplire.ru/jre/sep13/4/text.pdf
4. Д.И. Мирзоян. Основные особенности графических процессоров при математической и алгоритмической обработке данных в гетерогенных вычислительных системах. // I-й сборник научных трудов аспирантов, магистрантов и студентов кафедры корпоративных информационных систем / Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Московский государственный технический университет радиотехники, электроники и автоматики». – М., 2013. –128 с. Электронное издание, номер государственной регистрации 032102718 от 21 июня 2013г., с. 37-47
5. В.С. Горбунов, Г.С. Елизаров, Л.К. Эйсымонт. Обзор проектов экзафлопсных суперкомпьютеров за рубежом и в России, ограничения и перспективы роста. // Четвертый Московский Суперкомпьютерный Форум. Москва, 2013. [Электронный ресурс]. URL: http://it-sobytie.ru/events/1380
6. Лиходед Н.А. Локальность параллельных зернистых алгоритмов. Курс лекций. // Ф-т прикладной математики и информатики Белорусского государственного университета. [Электронный ресурс]. URL: http://www.fpmi.bsu.by/sm_full.aspx?guid=22523
7. Jens Breitbart Case studies on GPU usage and data structure design. // Kassel University. 2008 // [Электронный ресурс]. URL: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.189.2330&rep=rep1&type=pdf
8. Корнеев В.В., Павлухин П. В., Шевченко И.В. Графические процессоры в суперкомпьютерных системах. // Четвертый Московский Суперкомпьютерный Форум. Москва, 2013. [Электронный ресурс]. URL: http://it-sobytie.ru/events/1380
9. Андрианова Е.Г., Мирзоян Д.И. Опытная модификация алгоритма обработки данных «Движение к началу» (Move-To-Front, MTF) для гетерогенных вычислительных систем. // Научно-технический сборник научных материалов соискателей, докторантов и адъюнктов Академии Государственной противопожарной службы МЧС России,№2, 2012 г.,8 с.