БРЭГГОВСКИЕ СЕНСОРНЫЕ СВЧ-СТРУКТУРЫ НА КОАКСИАЛЬНОМ КАБЕЛЕ
А. Р. Насыбуллин, О. Г. Морозов, А. А. Севастьянов
Казанский национальный исследовательский технический университет им. А.Н. Туполева-КАИ
Получена 24 марта 2014 г.
Аннотация. В работе рассмотрены брэгговские СВЧ-структуры на коаксиальном кабеле, построенные на основе трансферта оптических технологий по аналогии с волоконными решетками Брэгга. Представлены методы их анализа и приведены результаты экспериментальных исследований. Впервые описаны симметричные двухрядные и трехрядные структуры. Показано, что добротность резонансного контура брэгговских СВЧ-структур на расчетной частоте возрастает с увеличением порядка резонанса (при кратном изменении длины структуры и периода неоднородностей) и числа рядов. Отдельно рассмотрены подходы и варианты использования указанных структур в сенсорных приложениях для измерения температуры и коэффициента диэлектрической проницаемости.
Ключевые слова: брэгговские СВЧ-структуры на коаксиальном кабеле, метод волновых матриц передачи, метод ориентированных графов, двухрядные и трехрядные структуры, спектральные характеристики, сенсорные приложения.
Abstract. In the paper the structures of the Bragg microwave coax designed on the base of optical technologies transfer similar to fiber Bragg gratings are discussed. Methods of its analysis and the results of experimental studies are presented. Symmetric two-row and three-row structures are firstly described. It is shown that the Q-factor of the microwave Bragg structure on the design frequency increases with the order of resonance (at fold change of the structure length and period of its irregularities) and a number of rows. Approaches and options for the use of these structures in sensory applications are examined especially for measuring the temperature and the dielectric permittivity.
Keywords: microwave Bragg structure on coaxial cable, the method of wave transmission matrices, the method of directed graphs, two-row and three-row structure, spectral characteristics, sensor applications.
Введение
Оптическое волокно и коаксиальный кабель – два типа цилиндрических направляющих систем электросвязи, объединяемых по условиям распространения электромагнитных волн общей теорией и физикой, отличающихся применением в различных частотных диапазонах [1]. Последнее десятилетие отмечается трансфертом технологий оптического диапазона в СВЧ-диапазон, характерной чертой которого является изготовление в СВЧ-диапазоне устройств подобных по структуре и свойствам приборам оптического диапазона, например, интерферометров Маха-Цендера, фотонных кристаллов, и, наконец, волоконных решеток Брэгга [2-5].
Волоконная решетка Брэгга (ВРБ) – это периодическое или апериодическое возмущение эффективного показателя преломления в сердцевине оптоволокна. Как правило, ВРБ имеет длину порядка нескольких миллиметров или сантиметров [6]. Сам период модуляции составляет сотни нанометров или гораздо больше для длиннопериодных волоконных решеток.
Изменение показателя преломления приводит к отражению света, распространяющегося вдоль волокна в узком диапазоне длин волн, для которых выполняются условия Брэгга:
,
(1)
где λ – длина волны света в вакууме; neff – эффективный показатель преломления света в волокне; Λ – период решетки.
По сути, условие (1) означает, что волновое число решетки соответствует разности волновых векторов падающей и отраженной волн. В этом случае, комплексные амплитуды соответствующего поля отраженной волны из различных частей решетки находятся в фазе так, что они могут складываться конструктивно, это своего рода фазовый синхронизм. Даже слабая модуляция показателя преломления (с амплитудой, например, 10-4) [6] является достаточным для достижения почти полного отражения, если решетка достаточно длинная.
В радиочастотной области аналогом ВРБ можно считать СВЧ-структуры, представляющие собой, расположенные в направляющем волноводе периодические нерегулярности волнового сопротивления [7, 8]. В качестве направляющей системы может быть использован коаксиальный волновод, частным случаем такой структуры является брэгговская СВЧ-структура на коаксиальном кабеле (БСКК) [9, 10].
1. Брэгговские СВЧ-структуры на коаксиальном кабеле
Введение нерегулярностей в поперечных сечениях оси БСКК производится высверливанием отверстий во внешнем проводнике и диэлектрическом заполнении кабеля (рис. 1). Периодическое расположение отверстий с периодом между их центрами L приводит к отражениям распространяющейся электромагнитной волны (ЭМВ) от каждой нерегулярности. Суперпозиция отраженных волн формирует спектр отражения БСКК, содержащий кратные дискретные резонансы, определяемые условием Брэгга.
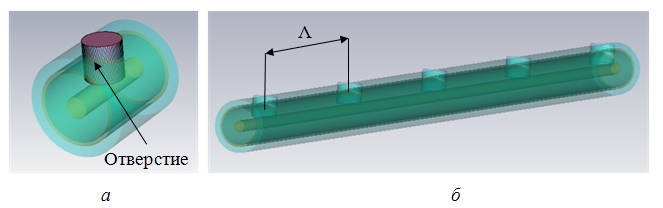
Рис. 1. Сегмент коаксиального кабеля с нерегулярностью (а) и вид БСКК (б).
Спектр отражения БСКК описывается следующим выражением:
где β+ и β- – постоянные распространения падающей и отраженной ЭМВ; m – порядок дифракции резонансной частоты; L и С – погонные индуктивность и емкость коаксиального кабеля. Характерные формы частотных зависимостей модуля и фазы коэффициентов отражения и передачи БСКК показаны на рис. 2.
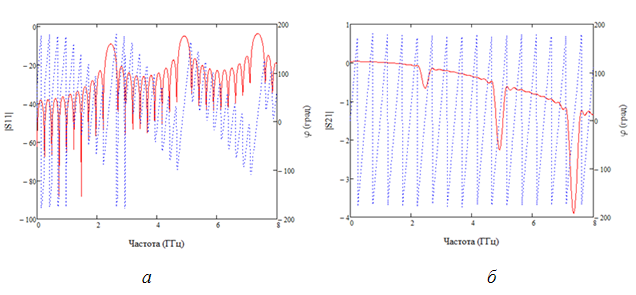
Рис. 2. Спектр модуля и фазы коэффициентов отражения (а) и передачи (б) БСКК.
На рис. 3,а представлена модель БСКК, предложенная в [10]. Помимо данной структуры нами для исследований была изготовлена БСКК с диаметрально расположенными отверстиями (рис. 3,б).
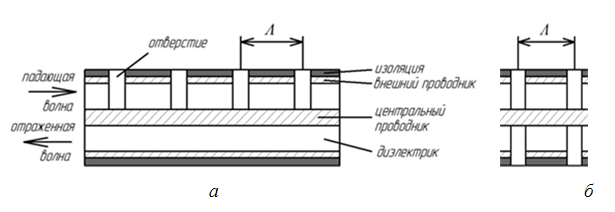
Рис. 3. Модели БСКК
с
односторонним (а) и с двусторонним (б) расположением отверстий.
В решении задач теоретического анализа частотных характеристик БСКК можно выделить три подхода.
1. Построение имитационной модели исследуемой БСКК в программе электродинамического моделирования с последующим расчетом частотных коэффициентов отражения и передачи средствами программного математического аппарата. В большинстве случаев в подобных приложениях используется расчет электромагнитных полей, описываемых дифференциальными уравнениями в частных производных, методом конечных разностей или конечных элементов. Положительной стороной данного подхода является высокая точность и достоверность получаемых результатов, недостатком можно указать большие вычислительные затраты и сложность оперативного регулирования параметрами электродинамической структуры.
2. Перечисленных недостатков лишен предложенный в работе [9] метод численного описания БСКК с помощью четырехполюсной волновой матрицы передачи для численного моделирования частотных характеристик отражения и передачи БСКК.
3. Анализ БСКК с использованием ориентированных графов. Этот метод позволяет получить характеристики отражения и передачи СВЧ-устройств в аналитическом виде.
Структуру БСКК можно представить как чередование участков однородного коаксиального волновода и участков с неоднородностью в виде отверстия во внешнем проводнике и диэлектрическом заполнении. В этом случае удобно использовать распространенный в теории цепей с распределенными параметрами метод декомпозиции на подсхемы.
На рис. 4 показано представление
отдельных участков БСКК в виде четырехполюсников, где 
и 
– напряжения падающих и отраженных волн на
соответствующих граничных сечениях n=1,2,3...
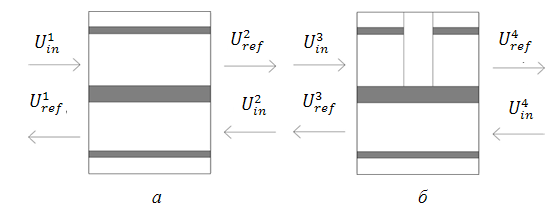
Рис. 4. Декомпозиционный подход к численному моделированию БСКК:
а – однородный участок; б – участок с неоднородностью.
Наиболее целесообразным в случае БСКК является описание элементарных участков с помощью волновых матриц передачи, при этом общая матрица будет являться произведением матриц отдельных элементов. Вывод матрицы передачи возможен из матрицы рассеяния, в силу их непосредственной связи. В силу взаимности и симметричности БСКК и ее составных элементарных участков, коэффициент отражения и передачи в прямом и обратном направлениях будут одинаковы: S11=S22, S21=S12.
Матрицы S рассеяния для каждого элементарного участка можно записать в виде:
, (3)
,
(4)
где 
– матрица рассеяния участка с
неоднородностью; 
– матрица рассеяния однородного
участка; 
и 
– комплексные коэффициенты отражения
и передачи каждой диэлектрической (воздушной) неоднородности; Λ – длина однородного
участка, равная периоду решетки; α – коэффициент затухания в кабеле; 
– постоянная распространения; ε –относительная диэлектрическая проницаемость
изоляции кабеля; c – скорость света в вакууме.
В соответствии с формулами взаимного перехода от волновой матрицы рассеяния к матрице Т передачи [11] получим:
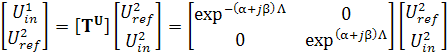, (5)
.
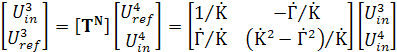(6)
Общая матрица T передачи БСКК будет определяться произведением матриц передачи участков с неоднородностью и однородных участков, возведенным в степень n, равную количеству отверстий в кабеле:
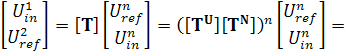
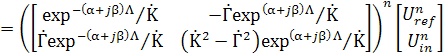, (7)
После получения конечной матрицы T коэффициенты отражения и передачи БСКК будут определяться как:
(8)
Если принять диаметр отверстий не более 5 мм, то в диапазоне частот до 10 ГГц неоднородности в кабеле можно считать сосредоточенными. При этом предположении возможен вывод коэффициентов отражения и передачи БСКК методом ориентированных графов для каскадного соединения N одинаковых параллельных неоднородностей с расстояниями между ними Λ.
На рис. 5 показана эквивалентная схема включения и ориентированный граф для БСКК, где Г – коэффициент отражения отдельного отверстия, а1 и b1 –падающая и отраженная волна на входе БСКК, bN – волна на выходе БСКК.
В результате решения данного ориентированного графа с помощью метода некасающегося контура [11] получим выражение для коэффициента отражения БСКК:
, (9)
при этом выражение для коэффициента отражения от неоднородности в общем виде можно представить как:
,
(10)
где y=g+jb – нормированная полная проводимость неоднородности.
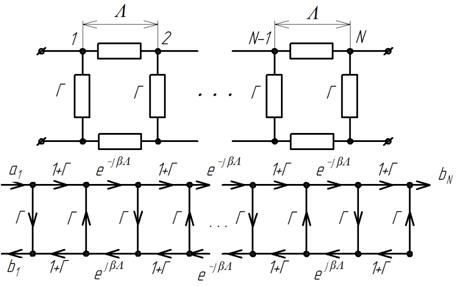
Рис. 5. Эквивалентная схема включения и ориентированный граф для БСКК
В силу сложности нахождения частотной зависимости комплексных коэффициентов отражения и передачи элементарного нерегулярного участка, удобно использовать для этих целей аппарат компьютерного моделирования, а далее применять матричный метод или метод графов, в зависимости от условий конкретной задачи.
3. Исследование характеристик и свойств БСКК
Для физического моделирования БСКК использовался коаксиальный кабель марки RG-213 (рис. 6) с волновым сопротивлением 50 Ом и погонной емкостью 98 пФ/м. Диаметр отверстий в диэлектрике кабеля составлял 4 мм, шаг отверстий – 42 мм. Кабель обладает следующими конструктивными диаметрами: центральной жилы – 2,25 мм, диэлектрика – 7,24 мм, оплетки – 8,1 мм, оболочки – 10,3 мм. Длина отрезка кабеля – 900 мм. Для коммутации с измерительным оборудованием кабель был оконцован разъемами N-типа.
Рис. 6. Брэгговская СВЧ-структура на коаксиальном кабеле RG213
Согласно выражению (2), выбранный период БСКК, равный 42 мм, определяет резонансную частоту 1-го порядка – 2450 МГц, соответствующую разрешенной частоте воздействия для промышленной СВЧ-обработки. Предварительная оценка резонансных свойств БСКК была получена с помощью моделирования идеализированного отрезка коаксиальной линии в специализированном программном пакете для исследования электродинамических процессов CST Microwave Studio. Моделирование проводилось для БСКК, представленной на рис. 3,а, для двух значений периода решетки – 42 мм и 84 мм, определяющих резонансную частоту 2450 МГц 1-го и 2-го порядка, соответственно. Количество отверстий в обоих случаях составляло 21. Полученные зависимости коэффициента отражения S11 и коэффициента передачи S21 представлены на рис. 7.
Вид частотных характеристик коэффициента отражения указывает на то, что избирательность выше у той БСКК, для которой резонансная частота выше 1-го порядка. Полоса частот по уровню -3dB в области резонансной частоты 2450 МГц для решетки с периодом 42 мм составляет 152 МГц, для решетки с периодом 84 мм – 86 МГц. Дальнейшее увеличение добротности системы требует пропорционального увеличения количества отверстий и длины кабеля, сопровождающееся уменьшением уровня коэффициента отражения на центральной частоте контура. Оптимальная конструкция БСКК с заданными свойствами определяется выбором компромисса между полосой пропускания контура и значением коэффициента отражения на резонансной частоте.
Рис. 7. Коэффициенты БСКК:
передачи (а) и отражения (б) для периода 42 мм,
передачи (в) и отражения (г) для периода 84 мм
Исследование экспериментальных частотных характеристик БСКК проводилось на векторном анализаторе спектра с функцией двухпортового анализа цепей Rohde & Schwarz FSH8 (рис. 8), обладающий диапазоном измеряемых частот от 100 кГц до 8 ГГц.
Рис. 8. Стенд для измерений. Рис. 9. Модель трехрядной БСКК.
Более высокую избирательность показали БСКК с периодом 42 мм и отверстиями, расположенными симметрично относительно центрального проводника (рис. 3,б) и под углом 120° (рис. 9), для которых зависимости коэффициента отражения показаны на рис. 10.
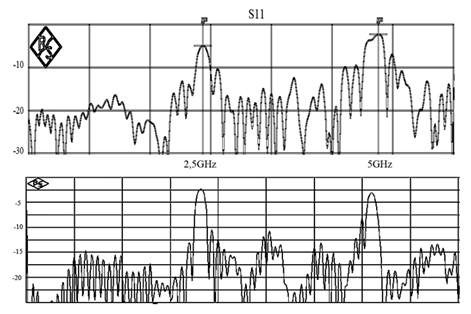
Рис. 10. Коэффициент отражения для БСКК
с двусторонним расположением отверстий (вверху)
и с расположением отверстий под
углом 120° (внизу).
Для последнего случая полоса пропускания контура отражения по уровню -3dB для первого резонанса составила 122 МГц. Последующие исследования в направлении улучшения резонансных характеристик и уменьшения влияния боковых лепестков связаны с организацией специальных видов БСКК с апериодическим расположением отверстий вдоль продольной оси кабеля и с расположением отверстий в поперечном сечении под различными углами.
4. Сенсорные приложения БСКК
Помимо явно выраженной практической направленности БСКК для решения задач фильтрации и преобразования СВЧ-сигналов, перспективным направлением их использования можно назвать измерение и контроль параметров материальных сред и физических полей. Например, в работе [9] предложен мониторинг строительных конструкций на базе БСКК с измерениями деформаций в диапазоне до 50000 με.
Перспективными направлениями применения БСКК являются измерение температуры и электрофизических параметров материалов и веществ, включая вещественную и мнимую части коэффициента диэлектрической проницаемости (КДП) и проводимость.
Подходы к контролю температуры можно представить двумя вариантами. В основе первого лежит зависимость диэлектрической проницаемости внутреннего заполнения БСКК от температуры при соприкосновении поверхности кабеля с контролируемой средой (рис. 11,а). Информация о значении температуры может быть выявлена по характеристикам коэффициентов отражения и передачи БСКК.
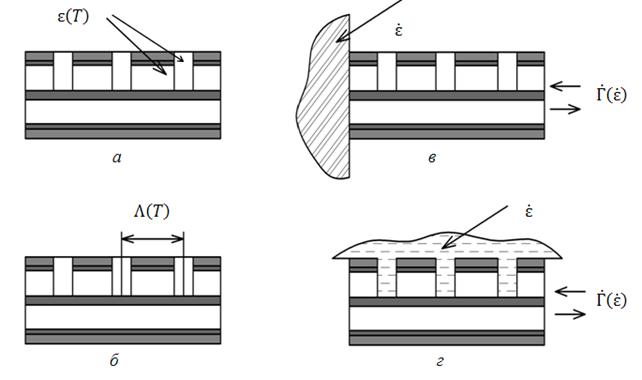
Рис. 11. Варианты сенсорных
применений БСКК:
измерение температуры по
функциональным зависимостям КДП (а) и периода (б) структуры;
измерение КДП при отражение от торца (в) и заполнении неоднородностей (г)
структуры.
Второй вариант основан на факте наличия у каждого материала, из которого состоит БСКК, своего коэффициента температурного уширения. В этом случае результатом температурного воздействия будет изменение периода решетки Λ и как следствие смещение резонансной частоты (рис. 11,б). Недостатками подобных вариантов температурного контроля можно назвать ограниченный диапазон измеряемых величин, невысокая точность измерения. Повышение точности измерений возможно при использовании специальных типов коаксиальных решеток, изготовленных из материалов с известными температурными и диэлектрическими свойствами.
В основе двух предлагаемых подходов к измерению КДП лежит зависимость частотных характеристик коэффициента отражения и передачи БСКК от параметров внешних воздействий. Первый заключается в соприкосновении одного из торцов БСКК с поверхностью исследуемого материала, в результате чего произойдет изменение коэффициента отражения БСКК функционально зависимое от свойств материала, по которому возможно определение его КДП (рис. 11,в). Второй подход основан на измерениях при заполнении отверстия или отверстий БСКК исследуемым веществом. В результате преобразования комплексной проводимости неоднородности изменяется форма частотной характеристики коэффициента отражения и передачи БСКК, характер которых будет указывать на значения диэлектрических параметров внешней среды (рис. 11,г). Измерение КДП можно осуществлять в диапазоне рабочих температур коаксиального кабеля, так при использовании фторопластового кабеля температурный предел достигает 400 °С. Нами БСКК использовались в качестве преобразователя в информационно-измерительной цепи контроля КДП реагирующей смеси, изменяющейся в процессе деполимеризации ПЭТФ в электродинамических реакторах [12-17].
Заключение
В работе рассмотрены БСКК, построенные на основе трансферта оптических технологий по аналогии с волоконными решетками Брэгга.
В силу сложности нахождения частотной зависимости комплексных коэффициентов отражения и передачи элементарных неоднородных участков, удобно использовать для синтеза БСКК аппарат компьютерного моделирования, а далее для анализа применять матричный метод или метод графов в зависимости от условий конкретной задачи.
Впервые описаны симметричные двухрядные и трехрядные структуры. Вид частотных характеристик коэффициента отражения указывает на то, что избирательность лучше у той БСКК, для которой резонансная частота выше 1-го порядка. Полоса частот по уровню -3dB в области резонансной частоты 2450 МГц для решетки с периодом 42 мм составляет 152 МГц (резонанс 1-го порядка), для решетки с периодом 84 мм – 86 МГц (резонанс 2-го порядка). Дальнейшее увеличение добротности системы требует пропорционального увеличения количества отверстий и длины кабеля, сопровождающееся уменьшением уровня коэффициента отражения на центральной частоте контура. При увеличении рядности БСКК полоса пропускания контура отражения по уровню -3dB для резонанса 1-го порядка составила 122 МГц с увеличением коэффициента отражения в 2 раза. Таким образом, оптимальная конструкция БСКК с заданными свойствами определяется выбором компромисса между полосой пропускания контура и значением коэффициента отражения на резонансной частоте, определяемых длиной структуры и ее рядностью. Дальнейшее улучшение резонансных характеристик и уменьшение влияния боковых лепестков возможно при синтезе специальных видов БСКК с апериодическим расположением отверстий вдоль продольной оси кабеля и с расположением отверстий в поперечном сечении под различными углами.
БСКК находят достаточно широкое применение как для фильтрации и обработки СВЧ-сигналов, так и в сенсорных приложения для измерения широкодиапазонных деформации в системах структурного мониторинга инженерно-технических сооружений. В статье отдельно рассмотрены подходы и варианты использования указанных структур в сенсорных приложениях для измерения температуры и коэффициента диэлектрической проницаемости. Для первых могут быть использованы керамические коаксиальные кабели, для вторых – коаксиальные кабели, покрытые специальными антикоррозионными, износостойкими и, например, олеофобными или гидрофобными покрытиями.
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации в рамках государственного задания на оказание услуг (выполнение работ) по организации научных исследований, выполняемых Казанским национальным исследовательским техническим университетом на кафедре телевидения и мультимедийных систем и в научно-исследовательском институте прикладной электродинамики, фотоники и живых систем (программа «Фотоника»).
Литература
1. Gloge D. Optical fiber technology. New York, IEEE Press, 1976.
2. Sanchez-Lopez M.M., Sanchez-Merono A., Arias J., Davis J.A., and I. Moreno, “Observation of superluminal and negative group velocities in a Mach–Zehnder interferometer” // Appl. Phys. Lett. 2008. Vol. 93, No 7. P. 074102 (2008).
3. Doiron S., Giller C., Beaudoin N., Haché A., “A periodic structure for electronic signals and demonstration of electronic lasing” // Am. J. Phys. 2008. Vol. 76. P. 996-1001.
4. Sun S., Chen G., “A novel TDR based coaxial cable sensor for crack/strain sensing in reinforced concrete structures” // IEEE Transactions on Instrumentation and Measurement. 2009. Vol. 58, No 8. P. 2714-2724.
5. Zhi Z., Yuan L., Peng Z. and Dyshlyuk A., “Novel coaxial cable Bragg grating” // Pacific Science Review. 2011. Vol. 13, No. 3. P. 196-199.
6. Васильев, С.А. Волоконные решетки показателя преломления и их применения / С.А. Васильев, О.И. Медведков, И.Г. Королев, А.С. Божков, А.С. Курков, Е.М. Дианов // Квантовая электроника. – 2005. – Т. 35, № 12. – С. 1085-1103.
7. Joannopoulos J.D., Villeneuve P.R., and Fan S., “Photonic crystals: Putting a new twist on light” // Nature. 1997. Vol. 386, No 6621. P. 143-149.
8. Munday J.N. and Robertson W.M., “Slow electromagnetic pulse propagation through a narrow transmission band in a coaxial photonic crystal” // Appl. Phys. Lett. 2003. Vol. 83, No 5. P. 1053.
9. Jie Huanga, Tao Weia, Xinwei Lana, Jun Fanb, Hai Xiao, “Coaxial cable Bragg grating sensors for large strain measurement with high accuracy” // Proc. of SPIE. 2012. Vol. 8345. P. 83450Z.
10. Tao Wei, Songping Wu, Jie Huang, Hai Xiao, and Jun Fan, “Coaxial cable Bragg grating” // Appl. Phys. Lett. 2011. Vol. 99. P. 113517.
11. Силаев М.А., Брянцев С.Ф. Приложение матриц и графов к анализу СВЧ устройств. М.: Изд-во «Советское радио», 1970. – 248 с.
12. Морозов, О.Г. Микроволновые технологии в процессах переработки и утилизации бытовых полимерных отходов / О.Г. Морозов, Р.Р. Самигуллин, А.Р. Насыбуллин // Известия Самарского научного центра Российской академии наук. - 2010. - Т. 12 (33). - № 4(3). - С. 580-582.
13. Морозов, О.Г. Микроволновая обработка термореактивных и термопластичных полимеров /О.Г.Морозов, Г.А.Морозов, Р.Р. Самигуллин, А.Р. Насыбуллин // Физика волновых процессов и радиотехнические системы. - 2011. - № 3. - С. 114-121.
14. Морозов, О.Г. Функциональные адаптивные СВЧ технологии в задачах переработки термопластичных полимерных материалов / О.Г. Морозов, Г.А. Морозов, А.Р. Насыбуллин [и др.] // Вестник Поволжского государственного технологического университета. Серия: Радиотехнические и инфокоммуникационные системы. - 2011. - № 3. - С.13-25.
15. Морозов, О.Г. Выбор оптимальной структуры построения СВЧ-комплекса обработки термореактивных композитных материалов / О.Г. Морозов, Г.А. Морозов, А.Р. Насыбуллин [и др.] // Известия Самарского научного центра Российской академии наук. - 2012. - Т. 14 (35). - № 1(2). - С. 525-529.
16. Морозов, О.Г. Резонансный метод мониторинга технологического процесса отверждения полимеров / О.Г. Морозов, Г.А. Морозов, А.Р. Насыбуллин [и др.] // Вестник Поволжского государственного технологического университета. Серия: Радиотехнические и инфокоммуникационные системы. ¾ 2012. ¾ № 1. ¾ С.67¾75.
17. Морозов, О.Г. Резонансные методы мониторинга технологических процессов отверждения полимеров в функционально адаптивных СВЧ-реакторах / О.Г. Морозов, Г.А. Морозов, А.Р. Насыбуллин [и др.] // Известия Самарского научного центра Российской академии наук. - 2012. - Т. 14 (35). - № 1(2). - С. 568-572.