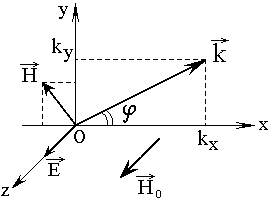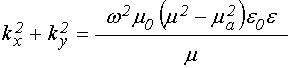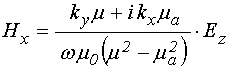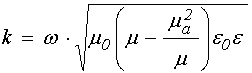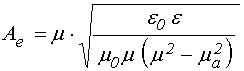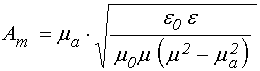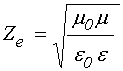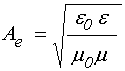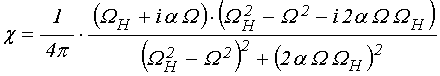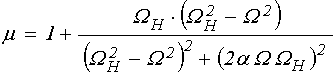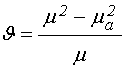УДК 537.874; 537.624
ПРОСТРАНСТВЕННОЕ РАСПРЕДЕЛЕНИЕ АМПЛИТУД ВНЕШНИХ И ВНУТРЕННИХ ВОЛН В ОГРАНИЧЕННОЙ МНОГОСЛОЙНОЙ СТРУКТУРЕ С ПЕРИОДИЧЕСКОЙ НЕОДНОРОДНОСТЬЮ
ЧАСТЬ 3. ЭЛЕКТРОМАГНИТНАЯ ВОЛНА В МАГНИТНОЙ СРЕДЕ
И. В. Антонец 1, В. Г. Шавров 2, В. И. Щеглов 2
1 Сыктывкарский государственный университет, Сыктывкар
2 Институт радиотехники и электроники РАН, Москва
Статья получена 10 февраля 2015 г.
Аннотация. Методом пошагового алгоритма рассмотрено распространение электромагнитных волн прямого и обратного направлений в многослойной структуре с периодической неоднородностью, барьеры которой обладают магнитодиэлектрическими свойствами. Показано, что в такой среде возможно распространение двух независимых волн – гиромагнитной и гироэлектрической. Рассмотрено отражение и прохождение гиромагнитной волны при падении на плоскую границу раздела двух сред с магнитными параметрами. Получены амплитуды отраженной и проходящей волн, выраженные через адмиттансы сред. Введен в рассмотрение «параметр расходимости», представляющий собой комбинацию из компонент тензора магнитной проницаемости. Показано, что в случае отрицательного знака параметра расходимости распространение гиромагнитной волны невозможно. Рассмотрен баланс потоков энергии распространяющихся волн на структуре в целом. В широком диапазоне рассмотрена частотная зависимость амплитуд волн обоих направлений. В спектре распространения выявлено появление широкой линии, обусловленной магнитными свойствами среды.
Ключевые слова: распространение волн, периодическая структура, частотный спектр, магнитодиэлектрическая среда.
Abstract. Electromagnetic waves of forward and backward directions propagating in the multi-layer structure with periodical nonuniformity having magnetodielectric barriers are investigated by the method of successive steps. It is shown that in this structure the propagation of two independent waves – gyromagnetic and gyroelectric types – is possible. The reflection and propagation of gyromagnetic wave incident upon the plane boundary between two magnetic media is investigated. The reflected and propagated waves amplitudes, described through the media admittances, are found. The “parameter of discrepancy” consisted of permeability tensor components combination is introduced into consideration. It is shown that in the case when the parameter of discrepancy is negative the gyromagnetic wave propagation is impossible. The balance of energy flow for waves propagating on the structure as a whole is investigated. In large frequency range the frequency dependence of both wave directions is investigated. The appearance of the broad line depending on magnetic properties of medium is found in propagation spectrum.
Key words: wave propagation, multi-layer structure, periodical nonuniformity, frequency spectrum, magnetodielectric medium.
Введение
В двух предыдущих частях настоящей работы [1,2] было рассмотрено пространственное распределение амплитуд внешних и внутренних волн прямого и обратного направлений в ограниченной многослойной структуре с периодической неоднородностью меандрового вида. В качестве инструмента исследования был использован пошаговый алгоритм [3-6], позволяющий удобным путем как получать аналитические выражения для амплитуд волн, так и рассчитывать распределение этих амплитуд численно.
Первая часть работы [1] была посвящена одномерным волнам, являющимся элементарным аналогом многих типов волн в различных средах. Введен эквивалент периодической многослойной среды как структуры, состоящей из одинаковых барьеров, разделенных одинаковыми промежутками. Были рассмотрены особенности распространения волн, связанные с периодичностью структуры, выявлен эффект «вторичной модуляции», интерпретированный на основе многорезонаторных свойств структуры. Исследованы амплитуды волн прямого и обратного направлений при изменении координаты или номера слоя структуры, а также среднего волнового числа. Рассмотрена неоднородность пилообразного вида, в том числе влияние формы зубьев пилы на условия распространения волн. Рассмотрено распределение амплитуд в случае большого изменения соотношения между волновыми числами сред, составляющих структуру. Исследована пространственная модуляция амплитуды, в характере которой выявлены пять основных режимов: синусоидальный, полусинусоидальный, линейный, экспоненциальный, а также синусоидальный с верхним пределом. Для объяснения особенностей пространственной модуляции предложена аналогия с цепочкой последовательно соединенных связанных резонаторов.
Во второй части работы [2] проведенные исследования были обобщены на случай электромагнитных волн. Пошаговый алгоритм видоизменен применительно к ситуации волн, распространяющихся в многослойной периодической структуре, свойства которой определяются электродинамическими адмиттансами составляющих ее сред. Исследованы частотные зависимости амплитуд волн прямого и обратного направлений, а также трансформация частотных характеристик при изменении числа барьеров. Исследовано распределение амплитуд волн во внутренних слоях структуры, выявлены два главных вида распределения – синусоидальное и экспоненциальное. Для широкого диапазона частот введены определения сильной и слабой неоднородностей и получен критерий перехода между ними. Рассмотрена трансформация частотных зависимостей в широком интервале изменения соотношения проницаемостей слоев. Выявлено поджатие частотного спектра к своему нижнему концу при увеличении этого соотношения.
Упомянутая вторая часть работы [2] посвящена исследованию электромагнитных волн в многослойной среде, из всех электродинамических параметров которой меняется лишь диэлектрическая проницаемость, тогда как магнитная проницаемость и проводимость остаются постоянными. При этом магнитная проницаемость полагалась равной единице, а проводимость вообще отсутствовала. То есть полученные там результаты применимы к распространению волн радиочастотного или оптического диапазона в многослойной структуре, представляющей собой набор слоев из диэлектрика. Магнитные свойства вещества оставались за пределами поля зрения, тогда как хорошо известно, что в СВЧ диапазоне ряд материалов, в первую очередь ферритов, оставаясь диэлектриками, проявляют ярко выраженные магнитные свойства, благодаря явлению ферромагнитного резонанса (ФМР) [7-9]. В частности, магнитная проницаемость таких материалов на определенных частотах может достигать многих десятков, сотен и даже тысяч, оставляя далеко позади диэлектрическую проницаемость традиционных диэлектриков в том же диапазоне.
Некоторые особенности влияния магнитной проницаемости на распространение волн в слоистых магнитных средах, такие как аномалии закона Брюстера и потоков энергии, отмечены в работе [10], однако проведенное там рассмотрение крайне неполно.
В соответствии с этим настоящая работа посвящена более подробному рассмотрению особенностей распространения электромагнитных волн в ограниченных периодических многослойных структурах, обладающих наряду с диэлектрическими также магнитными свойствами. В основу рассмотрения положена бигиротропная среда, некоторые свойства которой для безграничного или ограниченного одной плоскостью случаев рассматривались в работах [11,12]. Отражение и прохождение волн для случаев одной и двух границ между средами, обладающими магнитной гиротропией в условиях ориентационного перехода, рассматривались в работах [13,14]. В настоящей работе рассмотрен более общий случай, когда структура представляет собой периодический набор из ограниченного числа слоев, обладающих гиротропными магнитными свойствами.
1. Геометрия задачи
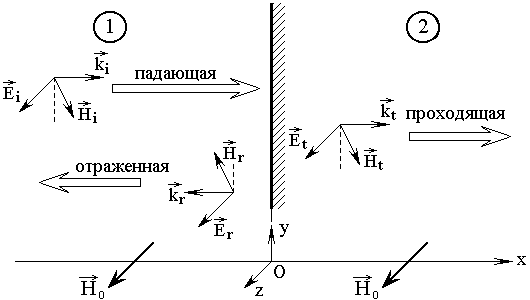
Геометрия задачи совпадает с приведенной в первых двух частях настоящей работы [1, 2]. Ее схема показана на рис.1. Рассматривается симметричная меандровая структура, в которой неоднородность представляет собой периодически расположенные одинаковые прямоугольные барьеры, с одинаковыми промежутками между ними.
Рис.1. Общая схема ограниченной многослойной структуры с периодической неоднородностью меандрового вида. Цифры в кругах – номера слоев (сред).
Структура содержит
два вида сред, обозначаемых индексами «![]() » и «
» и «![]() », каждый из которых имеет собственные
значения диэлектрических
», каждый из которых имеет собственные
значения диэлектрических ![]() ,
, ![]() и магнитных
и магнитных ![]() ,
, ![]() проницаемостей. В данном рассмотрении
ограничимся диэлектрическими средами, то есть положим проводимости обеих сред
равными нулю:
проницаемостей. В данном рассмотрении
ограничимся диэлектрическими средами, то есть положим проводимости обеих сред
равными нулю: ![]() . По вертикальной оси отложены
значения адмиттансов сред
. По вертикальной оси отложены
значения адмиттансов сред ![]() . Остальные обозначения
совпадают с приведенными в [1, 2].
. Остальные обозначения
совпадают с приведенными в [1, 2].
2. Электромагнитные волны в магнитной среде
Главной задачей настоящей работы является рассмотрение распространения электромагнитных волн в описанной в предыдущем разделе структуре, составляющие среды которой обладают магнитными свойствами. В работе [1] рассмотрение проведено на основе волнового числа, которое для одномерной волны является определяющим параметром. В работе [2] такое же рассмотрение проведено для электромагнитных волн, где роль определяющего параметра выполняет частота.
Рассматриваемый здесь случай магнитных сред является частным проявлением ситуации, описанной в этой работе, поэтому математический аппарат будет тем же самым [2]. Как и в работе [2], ограничимся случаем нормального падения волны, а также будем полагать все среды однородными. Диэлектрические свойства сред положим скалярными, магнитные же как скалярными, так и гиротропными. Электродинамические свойства сред будем описывать с помощью адмиттансов, а при расчете амплитуд воспользуемся методом пошагового алгоритма [15-18], схема которого для электромагнитных волн подробно описана в работе [2] и здесь не повторяется.
Главной задачей настоящей работы является выявление роли магнитных свойств вещества сред, составляющих многослойную структуру. Будем рассматривать магнитные диэлектрики, важнейшими представителями которых являются ферриты. Во многих таких материалах магнитные свойства, в отличие от диэлектрических, могут проявляться как в скалярном, так и в тензорном виде [7-9]. Поэтому сначала рассмотрим роль скалярной магнитной проницаемости, после чего обратимся к тензорной проницаемости, обусловленной свойством гиротропии.
3. Скалярная магнитная проницаемость
Рассмотрим сначала случай скалярной магнитной проницаемости. При рассмотрении будем следовать тому же порядку, что был принят в работе [2] для диэлектрической проницаемости. Основное внимание уделим частотным характеристикам распределения амплитуд волн в различных слоях структуры.
4. Частотные характеристики при малой проницаемости
Предварительное исследование показало, что для скалярной магнитной проницаемости выполняются те же критерии слабой и сильной неоднородности, что и для структур одномерной [1] и содержащей диэлектрические барьеры [2].
Основное различие между
частотными зависимостями, соответствующими слабой и сильной неоднородностям,
состоит в том, что при слабой неоднородности зависимости имеют плавный округлый
вид, тогда как при сильной они резко очерчены по верхнему и нижнему уровням, то
есть их вид близок к прямоугольному. В случае диэлектрических барьеров переход
от слабой неоднородности к сильной происходит при ![]() [2]. В
случае магнитных барьеров такой же переход происходит в том же интервале
изменения значений магнитной проницаемости, то есть при
[2]. В
случае магнитных барьеров такой же переход происходит в том же интервале
изменения значений магнитной проницаемости, то есть при ![]() .
.
В соответствии с тем же порядком действий, что был принят в работе [2], прежде всего исследовались частотные зависимости амплитуд волн прямого и обратного направлений в крайних слоях структуры. Было показано, что такие зависимости имеют квазирезонансный характер в виде большого центрального лепестка, с обеих сторон сопровождаемого меньшими лепестками-сателлитами.
Приведенные в работе [2]
на рис.2 зависимости нормированных амплитуд волн в крайних слоях структуры от
частоты падающей волны, соответствующие параметрам диэлектрических барьеров ![]() при
при ![]() ,
полностью повторяются тождественно при магнитных барьерах с параметрами:
,
полностью повторяются тождественно при магнитных барьерах с параметрами: ![]() при
при ![]() .
.
То же касается
трансформации частотных характеристик при изменении числа барьеров,
представленной в работе [2] на рис.3. То есть приведенные там кривые, соответствующие
![]() ,
, ![]() ,
полностью повторяются при
,
полностью повторяются при ![]() ,
, ![]() . Точно так же по мере увеличения числа
барьеров количество лепестков увеличивается, причем между основными появляются
те же промежуточные. Аналитические формулы, позволяющие рассчитать частоты
основных лепестков, положения их максимумов и минимумов между ними, также
полностью сохраняются. Можно полагать, что такая тождественность обусловлена
решающей ролью соотношения волновых чисел барьеров и промежутков, где значение
волнового числа, при скалярных обеих проницаемостях равное
. Точно так же по мере увеличения числа
барьеров количество лепестков увеличивается, причем между основными появляются
те же промежуточные. Аналитические формулы, позволяющие рассчитать частоты
основных лепестков, положения их максимумов и минимумов между ними, также
полностью сохраняются. Можно полагать, что такая тождественность обусловлена
решающей ролью соотношения волновых чисел барьеров и промежутков, где значение
волнового числа, при скалярных обеих проницаемостях равное
![]() ,
(1)
,
(1)
зависит от той и другой проницаемостей полностью идентично.
5. Распределение амплитуд в слоях при большой вариации параметров
Рассмотрим теперь распределение амплитуд в слоях при большом изменении параметров материала от слоя к слою. Ограничимся рассмотрением волн прямого направления, так как характер распределения волн обратного направления аналогичен, подобно таковому в работах [1,2]. Здесь, в отличие от предыдущего случая, между характеристиками, соответствующими вариации диэлектрической и магнитной проницаемостей, наблюдаются определенные различия, на рассмотрении которых и остановимся.
Обратимся к рис.2, где показано распределение нормированных амплитуд волн прямого направления в слоях от координаты при различных частотах падающей волны. Левый столбец (а,б,в,г) представляет собой распределения, имеющие место при большой диэлектрической проницаемости барьера и приведен здесь для сравнения. Правый столбец (д,е,ж,з) иллюстрирует распределения при большой магнитной проницаемости барьера.
Из сравнения столбцов
рисунка можно видеть, что те и другие распределения по форме повторяют друг
друга, то есть в обоих случаях имеются все четыре вида распределения:
синусоидальное (а,д), полусинусоидальное (б,е), линейное (в,ж) и экспоненциальное.
Более того, сходные распределения имеют место при одних и тех же частотах.
Существенным различием является тот факт, что амплитуды при большой магнитной
проницаемости превышают таковые при большой диэлектрической проницаемости примерно
в полтора-два раза. Кроме того, абсолютные величины амплитуд в последовательно
расположенных слоях как бы находятся в противофазе друг к другу, то есть при увеличении
соседствующих амплитуд в случае диэлектрической проницаемости, подобные
амплитуды в случае магнитной проницаемости уменьшаются и обратно. Так например,
амплитуда в слое №1 на рис.2а составляет ![]() , в
слое №2 –
, в
слое №2 – ![]() , в слое №3 –
, в слое №3 – ![]() Тогда
как подобные амплитуды на рис.2д равны соответственно
Тогда
как подобные амплитуды на рис.2д равны соответственно ![]() ,
,
![]() ,
, ![]() То
есть, если в слое №1, являющимся промежутком, нормированные амплитуды в обоих
случаях равны единице, что задается начальным возбуждением, то в слое №2,
являющимся барьером, амплитуда в случае диэлектрического барьера уменьшается, а
в случае магнитного – увеличивается. При переходе от барьера №2 к промежутку №3
амплитуда в случае диэлектрического барьера увеличивается, а в случае
магнитного – уменьшается.
То
есть, если в слое №1, являющимся промежутком, нормированные амплитуды в обоих
случаях равны единице, что задается начальным возбуждением, то в слое №2,
являющимся барьером, амплитуда в случае диэлектрического барьера уменьшается, а
в случае магнитного – увеличивается. При переходе от барьера №2 к промежутку №3
амплитуда в случае диэлектрического барьера увеличивается, а в случае
магнитного – уменьшается.
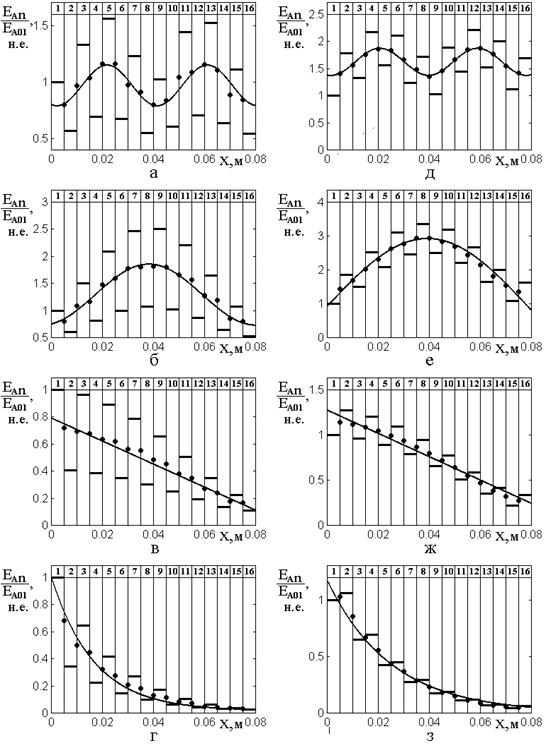
Рис.2. Распределение нормированных амплитуд волн прямого направления в слоях от координаты при различных частотах падающей волны. Цифры в верхнем ряду – номера слоев.
Параметры материала слоев: общие: ![]() ;
; ![]() ;
; ![]() ;
;
специфические: а,б,в,г – ![]() ;
; ![]() ; д,е,ж,з
–
; д,е,ж,з
– ![]() ;
; ![]() .
.
Частоты: а,д – ![]() ; б,е –
; б,е – ![]() ; в,ж
–
; в,ж
– ![]() ; г,з –
; г,з – ![]() .
.
Такое поведение амплитуд обусловлено последовательным переходом волны из менее плотной среды в более плотную и обратно при условии сохранения потока энергии [19-22]. Так в случае большой диэлектрической проницаемости барьер представляет собой среду более плотную, чем промежуток, а в случае большой магнитной – менее плотную. То есть в первом случае адмиттанс барьера по сравнению с адмиттансом промежутка велик, а во втором – мал. В математическом отношении это обусловлено тем, что в выражении для адмиттанса [2, форм.(3)] под корнем диэлектрическая проницаемость находится в числителе, а магнитная – в знаменателе.
Аналогичным образом, амплитуды в правом столбце в среднем выше амплитуд в левом из-за того, что в правом столбце относительно слоя №1, то есть слоя исхода волны, преобладают барьеры с малой плотностью, а в левом – с большой. Другими словами, усредненная по всей структуре плотность в правом столбце меньше плотности первого слоя, а в левом – больше. Таким образом, здесь выполняется то же правило увеличения амплитуды при переходе от менее плотной среды к более плотной и обратно, что и для соседствующих слоев, но уже относительно всей структуры в целом по отношению к плотности первого слоя, где амплитуда задана условиями возбуждения.
6. Тензорная магнитная проницаемость
Теперь, когда основные свойства электромагнитной волны в многослойной структуре со скалярной магнитной проницаемостью, в основном рассмотрены, обратимся к случаю, когда эта проницаемость имеет тензорный характер. В качестве предварительного этапа рассмотрим общие свойства электромагнитной волны в тензорной среде, необходимые для получения волновых чисел и адмиттансов в отдельных слоях структуры.
7. Волна в среде с тензорными параметрами
В большинстве сред магнитная проницаемость имеет гиротропный тензорный характер, поэтому рассмотрим сначала свойства электромагнитной волны в подобной среде. Для симметрии математического аппарата будем полагать среду бигиротропной, то есть такой, у которой как магнитная, так и диэлектрическая проницаемости обладают гиротропными свойствами.
Введем декартову систему
координат ![]() и направим ось
и направим ось ![]() вдоль
общей оси гиротропии, как это иллюстрируется рис.3.
вдоль
общей оси гиротропии, как это иллюстрируется рис.3.

Рис.3. Общая геометрия задачи. АВ – ось гиротропии.
В такой геометрии тензоры проницаемостей для бигиротропной среды имеют вид [7-9]:
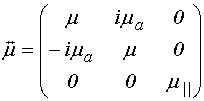 ;
(2)
;
(2)
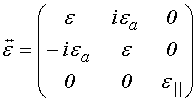 ;
(3)
;
(3)
Уравнения электродинамики в системе СИ в среде с тензорными параметрами имеют вид [23-29]:
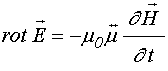 ;
(4)
;
(4)
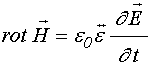 ,
(5)
,
(5)
где: ![]() и
и ![]() - электрическое и магнитное поля,
- электрическое и магнитное поля, ![]() и
и ![]() -
тензорные диэлектрическая и магнитная проницаемости среды,
-
тензорные диэлектрическая и магнитная проницаемости среды, ![]() и
и ![]() -
электрическая и магнитная постоянные в системе СИ.
-
электрическая и магнитная постоянные в системе СИ.
Среда предполагается
однородной, компоненты тензоров могут быть комплексными. Полагая зависимость от
времени в виде ![]() , получаем:
, получаем:
![]() ;
(6)
;
(6)
![]() .
(7)
.
(7)
Составляющие правых частей уравнений (6) и (7) имеют вид:
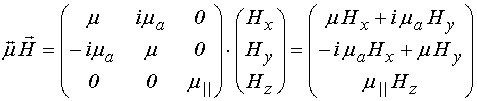 ;
(8)
;
(8)
 .
(9)
.
(9)
Записывая уравнения (6)-(7) по компонентам, получаем:
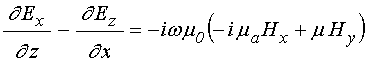 ;
(11)
;
(11)
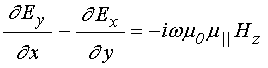 ;
(12)
;
(12)
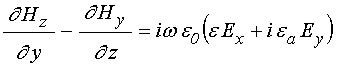 ;
(13)
;
(13)
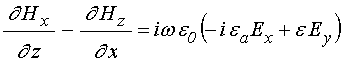 ; (14)
; (14)
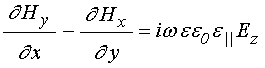 .
(15)
.
(15)
Положим, что координатно-временная составляющая волны имеет вид:
![]() .
(16)
.
(16)
При этом получаем:
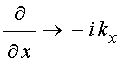 ,
,
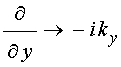 ,
, 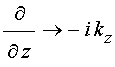 .
(17)
.
(17)
Из (10)-(15), раскрывая
скобки, перенося все слагаемые в левую часть и обозначая через ![]() ,
, ![]() амплитуды
полей волны, получаем:
амплитуды
полей волны, получаем:
![]() ; (19)
; (19)
![]() ; (20)
; (20)
![]() ; (21)
; (21)
![]() ; (22)
; (22)
![]() . (23)
. (23)
Это –
основная система уравнений для волны, распространяющейся в произвольном
направлении в бигиротропной среде, имеющей ось гиротропии вдоль оси ![]() . Частные случаи подобной системы для
несколько другой геометрии приведены в работах [7-9,
11,12]. В работах [13,14]
близкая система использовалась для исследования распространения волн в
композиционной среде, содержащей ферритовые элементы в условиях ориентационного
перехода. В настоящей работе эта система полагается в основу задачи о
многослойной среде с магнитными параметрами.
. Частные случаи подобной системы для
несколько другой геометрии приведены в работах [7-9,
11,12]. В работах [13,14]
близкая система использовалась для исследования распространения волн в
композиционной среде, содержащей ферритовые элементы в условиях ориентационного
перехода. В настоящей работе эта система полагается в основу задачи о
многослойной среде с магнитными параметрами.
8. Ориентация волнового вектора по нормали к оси гиротропии
Рассмотрим теперь более
простой частный случай – плоскую волну, волновой вектор которой ориентирован по
нормали к оси гиротропии, то есть в плоскости ![]() при
при ![]() . Из (18)-(23) получаем:
. Из (18)-(23) получаем:
![]() ;
(24)-1
;
(24)-1
![]() ;
(25)-2
;
(25)-2
![]() ;
(26)-3
;
(26)-3
![]() ;
(27)-4
;
(27)-4
![]() ;
(28)-5
;
(28)-5
![]() .
(29)-6
.
(29)-6
Эту систему уравнений
можно разбить на две независимые группы – одну, содержащую только ![]() ,
, ![]() ,
, ![]() - уравнения (24)-1, (25)-2, (29)-6, другую
– содержащую только
- уравнения (24)-1, (25)-2, (29)-6, другую
– содержащую только ![]() ,
, ![]() ,
, ![]() - уравнения (26)-3, (27)-4, (28)-5. Умножаем
уравнения (24)-1, (26)-3, (29)-6 на
- уравнения (26)-3, (27)-4, (28)-5. Умножаем
уравнения (24)-1, (26)-3, (29)-6 на ![]() , (27)-4 на
, (27)-4 на ![]() , (28)-5 на
, (28)-5 на ![]() , (25)-2
– оставляем без изменения. Объединяя уравнения в две группы, получаем две независимые
системы уравнений, каждая из которых описывает свою независимую волну:
, (25)-2
– оставляем без изменения. Объединяя уравнения в две группы, получаем две независимые
системы уравнений, каждая из которых описывает свою независимую волну:
ГИРОМАГНИТНАЯ:
![]() ;
(30)-1
;
(30)-1
![]() ;
(31)-2
;
(31)-2
![]() .
(32)-6
.
(32)-6
ГИРОЭЛЕКТРИЧЕСКАЯ:
![]() ;
(33)-4
;
(33)-4
![]() ;
(34)-5
;
(34)-5
![]() .
(35)-3
.
(35)-3
Поскольку
в данной задаче (многослойная структура с магнитными свойствами) главный
интерес представляют вариации именно магнитной проницаемости, то будем считать
диэлектрическую проницаемость скалярной величиной ![]() , то
есть в выражении (32) положим
, то
есть в выражении (32) положим ![]() ,
, ![]() . Таким образом, дальше ограничимся рассмотрением
только гиромагнитной волны.
. Таким образом, дальше ограничимся рассмотрением
только гиромагнитной волны.
9. Поля гиромагнитной волны
Рассмотрим гиромагнитную волну, геометрия полей для которой, совпадающая с принятой в [11-14], показана на рис.4.
Рис.4. Геометрия полей для гиромагнитной волны.
Здесь гиротропия обеспечивается
магнитным полем ![]() , направленным вдоль оси
, направленным вдоль оси ![]() , волновой вектор лежит в плоскости
, волновой вектор лежит в плоскости ![]() , электрическое поле волны направлено
вдоль оси
, электрическое поле волны направлено
вдоль оси ![]() , а магнитное – лежит в плоскости
, а магнитное – лежит в плоскости ![]() .
.
Система уравнений для ![]() ,
, ![]() ,
, ![]() имеет вид:
имеет вид:
![]() ;
(36)
;
(36)
![]() ;
(37)
;
(37)
Из условия равенства нулю детерминанта этой системы получаем дисперсионное соотношение:
Система (36)-(38) является
однородной (справа – нули) и содержит три уравнения для трех неизвестных,
поэтому два неизвестных можно выразить через третье. Полагая заданным ![]() , получаем систему для определения
, получаем систему для определения ![]() и
и ![]() :
:
![]() ;
(40)
;
(40)
![]() ;
(41)
;
(41)
![]() ,
(42)
,
(42)
решая которую находим поля гиромагнитной волны в виде:
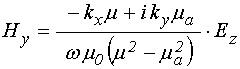 .
(44)
.
(44)
Здесь,
в отличие от изотропной среды, электромагнитная волна с волновым вектором вдоль
оси ![]() , кроме поперечных компонент
электрического и магнитного полей
, кроме поперечных компонент
электрического и магнитного полей ![]() и
и ![]() , имеет также продольную компоненту
магнитного поля
, имеет также продольную компоненту
магнитного поля ![]() . Причиной появления продольной
магнитной составляющей электромагнитной волны является магнитная гиротропия.
. Причиной появления продольной
магнитной составляющей электромагнитной волны является магнитная гиротропия.
10. Полярная система координат
Вводя
угол ![]() между волновым вектором
между волновым вектором ![]() и осью
и осью ![]() (рис.4)
получаем:
(рис.4)
получаем:
![]() ;
(45)
;
(45)
![]() ,
(46)
,
(46)
а также, учитывая, что:
![]() ,
(47)
,
(47)
из (39) получаем дисперсионное соотношение в следующем виде:
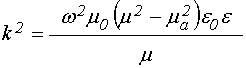 ,
(48)
,
(48)
откуда находим волновое число:
Из (43) и (44) – получаем компоненты вектора магнитного поля волны:
11. Импедансы и адмиттансы
Для удобства записи выражений (50)-(51), введем ИМПЕДАНСЫ:
ЛИНЕЙНОМАГНИТНЫЙ:
 ;
(52)
;
(52)
ГИРОМАГНИТНЫЙ:
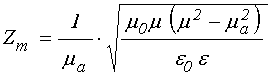 .
(53)
.
(53)
При этом поля волны (50)-(51) принимают вид:
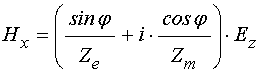 ;
(54)
;
(54)
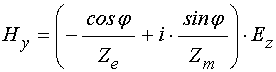 .
(55)
.
(55)
Наряду с импедансами, поля гиромагнитной волны можно выразить через обратные им величины – АДМИТТАНСЫ, что при расчете полей электромагнитной волны в многослойной структуре [2] составляет определенное удобство:
ЛИНЕЙНОМАГНИТНЫЙ:
ГИРОМАГНИТНЫЙ:
При этом поля (50) и (51) принимают вид:
![]() ;
(58)
;
(58)
![]() .
(59)
.
(59)
Для волны, волновой
вектор которой направлен вдоль оси ![]() , то есть при
, то есть при ![]() поля приобретают особенно простой вид:
поля приобретают особенно простой вид:
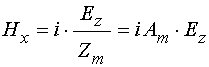 ;
(60)
;
(60)
 .
(61)
.
(61)
В выражениях (58) и (60)
коэффициент «![]() » при
» при ![]() -компонентах
магнитных полей означает изменение фазы на
-компонентах
магнитных полей означает изменение фазы на ![]() в
соответствии с выражением, следующим из формулы Эйлера:
в
соответствии с выражением, следующим из формулы Эйлера:
![]() ,
(62)
,
(62)
то есть:
![]() ;
(63)
;
(63)
![]() .
(64)
.
(64)
В случае изотропной
среды, то есть при ![]() , ее свойства определяются линейномагнитными
импедансом и адмиттансом, которые принимают классический вид [23-29]:
, ее свойства определяются линейномагнитными
импедансом и адмиттансом, которые принимают классический вид [23-29]:
При этом гиромагнитные импеданс и адмиттанс соответственно равны:
![]() ; (67)
; (67)
![]() . (68)
. (68)
12. Падение гиромагнитной волны на границу раздела двух сред
Рассмотрим в качестве предварительной задачи отражение и прохождение гиромагнитной волны через плоскую границу раздела двух сред при нормальном падении. Частные случаи подобной задачи для среды, содержащей ферритовые элементы в условиях ориентационного перехода, рассмотрены работах [13,14], здесь же проведем рассмотрение в более общем виде.
Геометрия задачи, аналогичная принятой в [13,14], иллюстрируется рис.5. Показаны заполненные волноведущими средами две области пространства 1 и 2, разделенные плоской границей между ними. Ось гиротропии, определяемая заданием постоянного магнитного поля, лежит в плоскости границы.
Волна падает из области 1
на границу раздела между областями 1 и 2, частично проходит в область 2 и
частично отражается обратно в область 1. Волновые векторы падающей ![]() , проходящей
, проходящей ![]() и
отраженной
и
отраженной ![]() волн перпендикулярны границе раздела
сред. Электрические поля всех волн параллельны плоскости раздела, магнитные
имеют две составляющие – параллельную и перпендикулярную плоскости раздела. Ось
координат
волн перпендикулярны границе раздела
сред. Электрические поля всех волн параллельны плоскости раздела, магнитные
имеют две составляющие – параллельную и перпендикулярную плоскости раздела. Ось
координат ![]() перпендикулярна границе раздела,
плоскость
перпендикулярна границе раздела,
плоскость ![]() совпадает с плоскостью раздела сред, ось
совпадает с плоскостью раздела сред, ось ![]() параллельна вектору электрического поля
падающей волны
параллельна вектору электрического поля
падающей волны ![]() .
.
Рис.5. Геометрия падения волны на плоскую границу раздела двух сред.
Полные координатно-временные зависимости полей имеют вид:
для отраженной волны: ![]() ; (70)
; (70)
для проходящей волны: ![]() . (71)
. (71)
Обозначая амплитуды
электрических полей падающей, отраженной и проходящей волн через ![]() ,
, ![]() и
и ![]() соответственно, получаем координатные
составляющие полей падающей, отраженной и проходящей волн, выраженные через
соответственно, получаем координатные
составляющие полей падающей, отраженной и проходящей волн, выраженные через ![]() ,
, ![]() ,
, ![]() (записываем через адмиттансы только
отличные от нуля компоненты):
(записываем через адмиттансы только
отличные от нуля компоненты):
для падающей волны:
![]() -
задано; (72)
-
задано; (72)
![]() ;
(73)
;
(73)
![]() ;
(74)
;
(74)
для отраженной волны:
![]() ;
(75)
;
(75)
![]() ;
(76)
;
(76)
![]() ;
(77)
;
(77)
для проходящей волны:
![]() ;
(78)
;
(78)
![]() ;
(79)
;
(79)
![]() .
(80)
.
(80)
Координатные составляющие полей по обе стороны от границы раздела сред равны:
в среде 1:
![]() ;
(81)
;
(81)
![]() ;
(82)
;
(82)
в среде 2:
![]() ;
(84)
;
(84)
![]() ;
(85)
;
(85)
![]() .
(86)
.
(86)
ГРАНИЧНЫЕ УСЛОВИЯ – непрерывность касательных составляющих полей на границе раздела, имеют вид:
![]() ,
(87)
,
(87)
![]() .
(88)
.
(88)
Подставляя (81)-(86) в (87), (88) и решая полученную систему относительно амплитуд отраженной и проходящей волн, а также учитывая (69)-(71), получаем поля всех волн в виде:
поля падающей волны:
![]() -
задано;
(89)
-
задано;
(89)
![]() ;
(90)
;
(90)
![]() ;
(91)
;
(91)
поля отраженной волны:
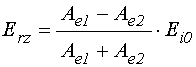 ;
(92)
;
(92)
 ;
(93)
;
(93)
 ;
(94)
;
(94)
поля проходящей волны:
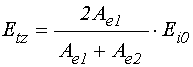 ;
(95)
;
(95)
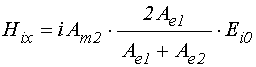 ;
(96)
;
(96)
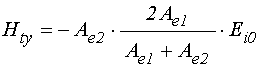 .
(97)
.
(97)
При этом для каждой из
волн определяющим является электрическое поле вдоль оси ![]() ,
а обе компоненты магнитного поля – поперечная вдоль оси
,
а обе компоненты магнитного поля – поперечная вдоль оси ![]() и
продольная вдоль оси
и
продольная вдоль оси ![]() , получаются в соответствии с
выражениями (90)-(91), (93)-(94), (96)-(97), причем для отраженной волны надо
учитывать изменение знака обеих этих составляющих за счет изменения направления
распространения, как это видно из рис.5.
, получаются в соответствии с
выражениями (90)-(91), (93)-(94), (96)-(97), причем для отраженной волны надо
учитывать изменение знака обеих этих составляющих за счет изменения направления
распространения, как это видно из рис.5.
Из выражений (89), (93) и (95) видно, что они с точностью до замены импедансов на адмиттансы совпадают с аналогичными выражениями полей для электромагнитной волны в изотропной среде [3-6]. Отсюда можно сделать вывод, что электрические поля волн в различных слоях многослойной структуры, содержащей гиротропные магнитные среды, подчиняются тем же законам распространения, что и поля в случае изотропных сред.
Это означает, что для определения полей волн в такой структуре можно использовать тот же пошаговый алгоритм, что и для одномерной волны, вариант которого для электромагнитной волны приведен в работе [2].
ЗАМЕЧАНИЕ. Проведенное рассмотрение выполнено для случая, когда направления осей гиротропии во всех слоях структуры совпадают. Случай несовпадения таких направлений может отличаться от приведенного здесь и требует отдельного рассмотрения, выходящего за рамки настоящей работы.
13. Тензор магнитной проницаемости
Применение пошагового
алгоритма требует предварительного вычисления адмиттансов (56)-(57), в случае
гиротропной магнитной среды выражаемых через компоненты тензора магнитной
проницаемости ![]() и
и ![]() . Рассмотрим
теперь конкретный вид этого тензора.
. Рассмотрим
теперь конкретный вид этого тензора.
Высокочастотные магнитные свойства материала описываются на основе модели прецессии вектора намагниченности. Для этого будем пользоваться уравнением движения для намагниченности Ландау-Лифшица с диссипативным членом в форме Гильберта [7-9]:
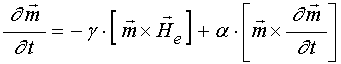 ,
(98)
,
(98)
где ![]() –
нормированный вектор намагниченности,
–
нормированный вектор намагниченности, ![]() –
намагниченность насыщения,
–
намагниченность насыщения, ![]() – гиромагнитная
постоянная,
– гиромагнитная
постоянная, ![]() – эффективное поле внутри магнетика,
– эффективное поле внутри магнетика, ![]() – параметр затухания Гильберта.
– параметр затухания Гильберта.
Решая это уравнение традиционным методом линеаризации [7-9], получаем компоненты тензора магнитной восприимчивости в виде:
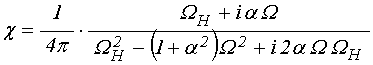 ;
(99)
;
(99)
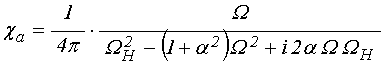 ,
(100)
,
(100)
где:
 ;
(101)
;
(101)
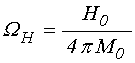 .
(102)
.
(102)
Полагая магнитные потери
достаточно малыми (![]() ) и освобождаясь от мнимости в
знаменателе, получаем:
) и освобождаясь от мнимости в
знаменателе, получаем:
 .
(104)
.
(104)
Для дальнейшего упрощения положим мнимые части в числителях обоих этих выражений равными нулю (при этом мы теряем фазу и частично потери, но для первого рассмотрения будем полагать это несущественным):
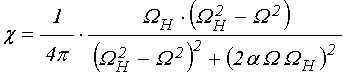 ;
(105)
;
(105)
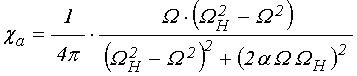 .
(106)
.
(106)
Учитывая, что магнитная проницаемость связана с восприимчивостью соотношением:
где ![]() –
единичный тензор, получаем компоненты тензора магнитной проницаемости в виде:
–
единичный тензор, получаем компоненты тензора магнитной проницаемости в виде:
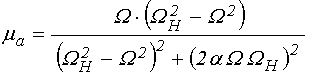 .
(109)
.
(109)
ЗАМЕЧАНИЕ. Динамическая магнитная восприимчивость вещества, обусловленная прецессией вектора намагниченности, традиционно рассчитывается в системе СГС [7-9]. Однако распространение электромагнитных волн в настоящей работе рассчитывается в системе СИ [23-29]. Правила перехода от одной системы к другой можно найти, например, в учебных монографиях [30,31]. При переходе к системе СИ восприимчивость (105)-(106) приобретает вид:
 ;
(110)
;
(110)
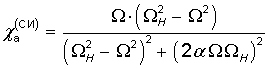 .
(111)
.
(111)
При этом проницаемость (107) вычисляется по формуле:
![]() ,
(112)
,
(112)
в результате чего формулы (108)-(109), используемые для расчета адмиттансов (56)-(57), остаются без изменения.
14. Характерные частоты
Отметим сначала некоторые параметры, важные для дальнейшего рассмотрения. Исходя из частотной зависимости компонент проницаемости, выделим следующие характерные частоты:
– частота, где обе компоненты проницаемости ![]() и
и ![]() в
отсутствие затухания расходятся, а при наличии затухания
в
отсутствие затухания расходятся, а при наличии затухания ![]() проходит через единицу, а
проходит через единицу, а ![]() – через нуль:
– через нуль:
– частота, где компонента
проницаемости ![]() в отсутствие затухания проходит
через нуль:
в отсутствие затухания проходит
через нуль:
![]() (114)
(114)
– частота, где параметр расходимости
![]() (рассмотрен подробно в разделе №15) в отсутствие
затухания проходит через нуль:
(рассмотрен подробно в разделе №15) в отсутствие
затухания проходит через нуль:
В дальнейшем, кроме особо
оговариваемых случаев, будем использовать следующие параметры магнитной среды:
поле: ![]() ; намагниченность:
; намагниченность: ![]() ;
гиромагнитная постоянная:
;
гиромагнитная постоянная: ![]() .
.
При этих параметрах характерные частоты имеют следующие значения:
![]() ;
;
![]() ;
; ![]() .
.
15. Параметр расходимости.
Важной характеристикой, в
значительной степени определяющей свойства распространения волн, является
параметр ![]() , условно названный нами «параметром
расходимости»:
, условно названный нами «параметром
расходимости»:
Этот параметр входит в подкоренные выражения для волнового числа (49) и адмиттанса (56)-(57). Так что волновое число и адмиттанс могут быть действительными только при положительности этого параметра. В случае его отрицательности волна не может распространяться.
Предварительное
рассмотрение показывает, что в отсутствие затухания на частоте ![]() этот параметр имеет особенность типа
расходимости, на частотах
этот параметр имеет особенность типа
расходимости, на частотах ![]() и
и ![]() меняет знак, то есть проходит через нуль.
В интервале между
меняет знак, то есть проходит через нуль.
В интервале между ![]() и
и ![]() этот
параметр отрицателен, то есть этот интервал для распространения волны запрещен.
В результате волновое число положительно везде на частотах ниже
этот
параметр отрицателен, то есть этот интервал для распространения волны запрещен.
В результате волновое число положительно везде на частотах ниже ![]() , кроме небольшой окрестности около
частоты
, кроме небольшой окрестности около
частоты ![]() , а также на частотах выше
, а также на частотах выше ![]() . Адмиттанс положителен только на частотах
ниже
. Адмиттанс положителен только на частотах
ниже ![]() и выше
и выше ![]() . Между
частотами
. Между
частотами ![]() и
и ![]() он не
существует (запрещенный интервал), а между частотами
он не
существует (запрещенный интервал), а между частотами ![]() и
и
![]() является действительным, но имеет отрицательный
знак.
является действительным, но имеет отрицательный
знак.
Таким образом, когда
параметр расходимости ![]() отрицателен, волновое число и
адмиттанс не существуют.
отрицателен, волновое число и
адмиттанс не существуют.
При принятых параметрах задачи
можно указать приближенные границы запрещенных и разрешенных участков. Так предварительное
рассмотрение показало, что при крайне слабом затухании (![]() )
в пределах исследованного интервала от
)
в пределах исследованного интервала от ![]() до
до ![]() запрещенные участки имеют частоты:
запрещенные участки имеют частоты: ![]() ;
; ![]() . При
этом разрешенные участки соответствуют частотам:
. При
этом разрешенные участки соответствуют частотам: ![]() ;
; ![]() ;
; ![]() . При
крайне сильном затухании
. При
крайне сильном затухании ![]() весь интервал частот разрешен.
весь интервал частот разрешен.
После такого краткого введения обратимся к рассмотрению роли затухания в распространении волны более подробно.
16. Три интервала параметра затухания
По свойствам распространения волн
можно выделить три характерных вида его поведения, различающихся значениями
параметра затухания ![]() . Интервалы значений
. Интервалы значений ![]() , определяющие эти свойства, можно условно
охарактеризовать затуханием «слабым», «средним» и «сильным». Численное
исследование позволило выявить два характерных значения параметра затухания,
разделяющего эти три области. Так при
, определяющие эти свойства, можно условно
охарактеризовать затуханием «слабым», «средним» и «сильным». Численное
исследование позволило выявить два характерных значения параметра затухания,
разделяющего эти три области. Так при ![]() и
и ![]() характерные значения равны:
характерные значения равны: ![]() и
и ![]() .
Слабое затухание соответствует интервалу
.
Слабое затухание соответствует интервалу ![]() ,
среднее – интервалу
,
среднее – интервалу ![]() , сильное – интервалу
, сильное – интервалу ![]() . Приведенные численные значения определяются
особыми точками характерных значений компонент тензора магнитной проницаемости
. Приведенные численные значения определяются
особыми точками характерных значений компонент тензора магнитной проницаемости ![]() и
и ![]() ,
вследствие чего являются резкими (в настоящей работе определялись с точностью
до четырех значащих цифр).
,
вследствие чего являются резкими (в настоящей работе определялись с точностью
до четырех значащих цифр).
Рассмотрим важные для
дальнейшего характерные частотные свойства компонент тензора проницаемости ![]() и
и ![]() ,
параметра расходимости
,
параметра расходимости ![]() , волнового числа
, волнового числа ![]() и адмиттанса
и адмиттанса ![]() в
упомянутых трех интервалах параметра затухания.
в
упомянутых трех интервалах параметра затухания.
Слабое затухание соответствует
интервалу ![]() . Обратимся к рис.6, где показаны
частотные зависимости характерных параметров распространения волн при параметре
затухания равном
. Обратимся к рис.6, где показаны
частотные зависимости характерных параметров распространения волн при параметре
затухания равном ![]() .
.
Из рис.6а видно, что обе
компоненты проницаемости проходят через нуль вблизи частоты ![]() . Более подробное исследование показывает,
что точно на частоте
. Более подробное исследование показывает,
что точно на частоте ![]() компонента проницаемости
компонента проницаемости ![]() проходит через единицу, а компонента
проходит через единицу, а компонента ![]() – через нуль. По обе стороны от этой
частоты при стремлении затухания к нулю обе компоненты расходятся на плюс-минус
бесконечность. Компонента
– через нуль. По обе стороны от этой
частоты при стремлении затухания к нулю обе компоненты расходятся на плюс-минус
бесконечность. Компонента ![]() проходит через нуль
вблизи частоты
проходит через нуль
вблизи частоты ![]() (здесь – несколько ниже, но при
(здесь – несколько ниже, но при
![]() проходит точно). Между
проходит точно). Между ![]() и
и ![]() величина
величина
![]() отрицательна. При увеличении частоты
отрицательна. При увеличении частоты ![]() стремится к единице, а
стремится к единице, а ![]() к нулю, то есть разность квадратов этих
компонент, находящаяся в числителе выражения для параметра расходимости
к нулю, то есть разность квадратов этих
компонент, находящаяся в числителе выражения для параметра расходимости ![]() (116), всегда положительна.
(116), всегда положительна.
На рис.6б приведена
частотная зависимость для параметра расходимости ![]() . Его
знак здесь определяется соотношением знаков компонент проницаемости
. Его
знак здесь определяется соотношением знаков компонент проницаемости ![]() и
и ![]() .
Видно, что этот параметр в областях ниже частоты
.
Видно, что этот параметр в областях ниже частоты ![]() и выше
и выше
![]() положителен, а между
положителен, а между ![]() и
и ![]() –
отрицателен. Это означает, что волновое число и адмиттанс между
–
отрицателен. Это означает, что волновое число и адмиттанс между ![]() и
и ![]() определены
быть не могут. Небольшая особенность параметра при частоте
определены
быть не могут. Небольшая особенность параметра при частоте ![]() отражает прохождение
отражает прохождение ![]() и
и ![]() через
нуль, сопровождаемое по обе стороны от этой частоты расходимостью противоположных
знаков. При
через
нуль, сопровождаемое по обе стороны от этой частоты расходимостью противоположных
знаков. При ![]() подобную же расходимость испытывает и
подобную же расходимость испытывает и ![]() .
.
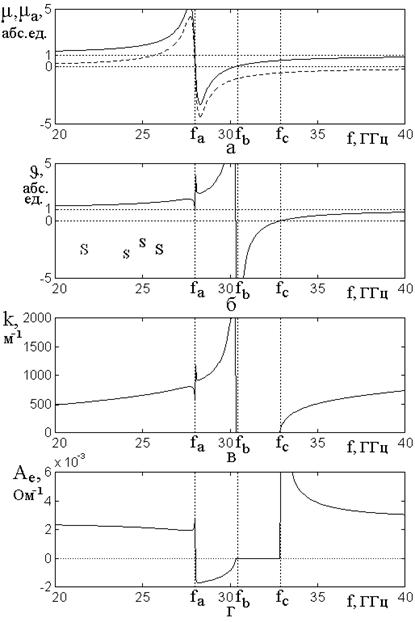
Рис.6. Частотные зависимости характерных параметров
распространения волны при слабом затухании: ![]() .
.
а – компоненты тензора проницаемости ![]() – сплошная линия,
– сплошная линия, ![]() –
пунктир;
–
пунктир;
б – параметр расходимости ![]() ; в –
волновое число
; в –
волновое число ![]() ; г – адмиттанс
; г – адмиттанс ![]() .
.
Горизонтальные точечные линии соответствуют нулю и
единице, вертикальные – значениям характерных частот ![]() ,
,
![]() ,
, ![]() .
.
На рис.6в приведена
частотная зависимость для волнового числа ![]() . Поскольку,
согласно (49), волновое число пропорционально квадратному корню из
. Поскольку,
согласно (49), волновое число пропорционально квадратному корню из ![]() , то его частотная зависимость также
подобна зависимости для
, то его частотная зависимость также
подобна зависимости для ![]() . Между частотами
. Между частотами ![]() и
и ![]() волновое
число не определено, а на частоте
волновое
число не определено, а на частоте ![]() – равно нулю в силу
равенства нулю на этой частое параметра
– равно нулю в силу
равенства нулю на этой частое параметра ![]() .
Небольшая особенность
.
Небольшая особенность ![]() на частоте
на частоте ![]() идентична подобной особенности
идентична подобной особенности ![]() .
.
На рис.6г приведена
частотная зависимость для адмиттанса ![]() . В соответствии с (56)
знак его определяется произведением корня из
. В соответствии с (56)
знак его определяется произведением корня из ![]() на
на ![]() . Поэтому в области между
. Поэтому в области между ![]() и
и ![]() , где
, где ![]() отрицательна (рис.6а), знак адмиттанса
отрицательна (рис.6а), знак адмиттанса ![]() тоже отрицательный. Между частотами
тоже отрицательный. Между частотами ![]() и
и ![]() адмиттанс
не определен в силу отрицательности
адмиттанс
не определен в силу отрицательности ![]() , а ниже
, а ниже ![]() и выше
и выше ![]() –
положителен. В положительной окрестности частоты
–
положителен. В положительной окрестности частоты ![]() адмиттанс
расходится, что обусловлено прохождением через нуль параметра
адмиттанс
расходится, что обусловлено прохождением через нуль параметра ![]() .
.
Таким
образом, можно сделать вывод, что при слабом затухании волна в магнитной среде
может распространяться ниже частоты ![]() и выше частоты
и выше частоты ![]() обычным порядком, то есть при
положительном адмиттансе, между частотами
обычным порядком, то есть при
положительном адмиттансе, между частотами ![]() и
и ![]() – при отрицательном адмиттансе, а
интервал частот между
– при отрицательном адмиттансе, а
интервал частот между ![]() и
и ![]() для
распространения волны является полностью запрещенным.
для
распространения волны является полностью запрещенным.
Среднее затухание соответствует
интервалу ![]() . Обратимся к рис.7, где показаны
частотные зависимости характерных параметров распространения волн при параметре
затухания равном
. Обратимся к рис.7, где показаны
частотные зависимости характерных параметров распространения волн при параметре
затухания равном ![]() .
.
Из рис.7а видно, что на
частоте ![]() , как и при слабом затухании, компонента
проницаемости
, как и при слабом затухании, компонента
проницаемости ![]() проходит через единицу, а
компонента
проходит через единицу, а
компонента ![]() – через нуль. По обе стороны от этой
частоты они проходят через небольшие экстремумы – ниже
– через нуль. По обе стороны от этой
частоты они проходят через небольшие экстремумы – ниже ![]() через
максимум, выше – через минимум. Обе зависимости подобны друг другу с учетом
сдвига
через
максимум, выше – через минимум. Обе зависимости подобны друг другу с учетом
сдвига ![]() вверх по отношению к
вверх по отношению к ![]() на единицу. Во всем интервале частот
на единицу. Во всем интервале частот ![]() положительна, тогда как
положительна, тогда как ![]() ниже
ниже ![]() положительна,
а выше – отрицательна.
положительна,
а выше – отрицательна.
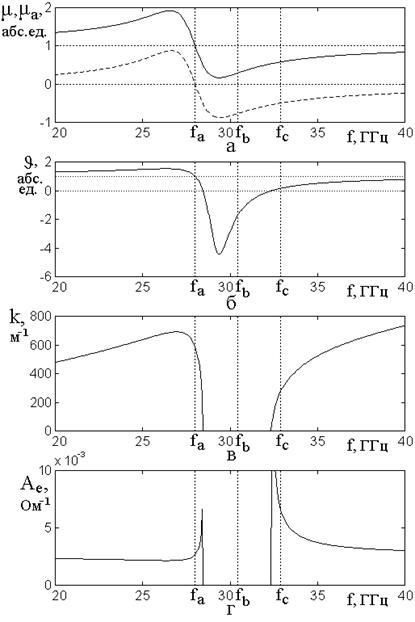
Рис.7. Частотные зависимости
характерных параметров распространения волны при среднем затухании: ![]() .
.
Все обозначения и остальные параметры – те же, что на рис.6.
В интервале частот,
начинающемся несколько выше ![]() и заканчивающимся несколько
ниже
и заканчивающимся несколько
ниже ![]() , абсолютная величина
, абсолютная величина ![]() превышает абсолютную величину
превышает абсолютную величину ![]() . В этом интервале разность квадратов
. В этом интервале разность квадратов ![]() , присутствующая в числителе выражения для
, присутствующая в числителе выражения для
![]() , отрицательна. Вне этого интервала по частоте
в обе стороны абсолютная величина
, отрицательна. Вне этого интервала по частоте
в обе стороны абсолютная величина ![]() всегда превышает
абсолютную величину
всегда превышает
абсолютную величину ![]() , то есть разность
, то есть разность ![]() всегда положительна.
всегда положительна.
На рис.7б приведена
частотная зависимость для параметра расходимости ![]() . Его
знак здесь определяется соотношением знаков компонент проницаемости
. Его
знак здесь определяется соотношением знаков компонент проницаемости ![]() и
и ![]() . Видно,
что этот параметр ниже частоты
. Видно,
что этот параметр ниже частоты ![]() , на которой
, на которой ![]() и
и ![]() проходят
через нуль, положителен. Несколько выше частоты
проходят
через нуль, положителен. Несколько выше частоты ![]() он
остается положительным, после чего меняет знак, оставаясь отрицательным почти до
частоты
он
остается положительным, после чего меняет знак, оставаясь отрицательным почти до
частоты ![]() , немного не доходя до которой снова меняет
знак, возвращаясь к положительному значению. Выше этого второго изменения знака
параметр
, немного не доходя до которой снова меняет
знак, возвращаясь к положительному значению. Выше этого второго изменения знака
параметр ![]() всегда остается положительным. Таким
образом, между
всегда остается положительным. Таким
образом, между ![]() и
и ![]() , несколько
отступая от этих частот, имеется широкая область отрицательных значений параметра
расходимости
, несколько
отступая от этих частот, имеется широкая область отрицательных значений параметра
расходимости ![]() . В этой области подкоренные выражения,
входящие в волновое число (49) и адмиттанс (56), отрицательны, то есть для
распространения волн эта область является запрещенной.
. В этой области подкоренные выражения,
входящие в волновое число (49) и адмиттанс (56), отрицательны, то есть для
распространения волн эта область является запрещенной.
На рис.7в приведена
частотная зависимость для волнового числа ![]() . Поскольку,
согласно (49), волновое число включает в себя квадратный корень из
. Поскольку,
согласно (49), волновое число включает в себя квадратный корень из ![]() , то в тех местах, где параметр
, то в тех местах, где параметр ![]() отрицателен, волновое число не определено.
На краях своей области определения волновое число стремится к нулю, что
обусловлено прохождением параметра
отрицателен, волновое число не определено.
На краях своей области определения волновое число стремится к нулю, что
обусловлено прохождением параметра ![]() через нуль.
через нуль.
На рис.7г приведена
частотная зависимость для адмиттанса ![]() . Здесь также между
. Здесь также между ![]() и
и ![]() ,
несколько отступя от этих частот, имеется широкая запрещенная область, определяемая
интервалом отрицательности параметра
,
несколько отступя от этих частот, имеется широкая запрещенная область, определяемая
интервалом отрицательности параметра ![]() . На краях этой области
адмиттанс стремится к бесконечности, что также обусловлено прохождением
параметра
. На краях этой области
адмиттанс стремится к бесконечности, что также обусловлено прохождением
параметра ![]() через нуль.
через нуль.
Таким
образом, можно сделать вывод, что при среднем затухании волна в магнитной среде
может распространяться ниже частоты ![]() и выше частоты
и выше частоты ![]() обычным порядком, то есть при
положительном адмиттансе. Однако между частотами
обычным порядком, то есть при
положительном адмиттансе. Однако между частотами ![]() и
и ![]() имеется широкая запрещенная область, края
которой близко примыкают к этим частотам, а волна может распространяться только
в близких окрестностях частот
имеется широкая запрещенная область, края
которой близко примыкают к этим частотам, а волна может распространяться только
в близких окрестностях частот ![]() и
и ![]() снизу и сверху соответственно.
снизу и сверху соответственно.
19. Затухание сильное
Сильное затухание
соответствует интервалу ![]() . Обратимся к рис.8,
где показаны частотные зависимости характерных параметров распространения волн
при параметре затухания равном
. Обратимся к рис.8,
где показаны частотные зависимости характерных параметров распространения волн
при параметре затухания равном ![]() .
.
Из рис.8а видно, что,
подобно случаям малого и среднего затухания, на частоте ![]() компонента
проницаемости
компонента
проницаемости ![]() проходит через единицу, а компонента
проходит через единицу, а компонента
![]() – через нуль. По обе стороны от этой
частоты обе компоненты проходят через небольшие экстремумы, которые здесь
однако выражены слабее, чем в случае среднего затухания. Обе зависимости также
подобны друг другу с учетом сдвига
– через нуль. По обе стороны от этой
частоты обе компоненты проходят через небольшие экстремумы, которые здесь
однако выражены слабее, чем в случае среднего затухания. Обе зависимости также
подобны друг другу с учетом сдвига ![]() вверх по отношению к
вверх по отношению к ![]() на единицу. Как и ранее, во всем
интервале частот
на единицу. Как и ранее, во всем
интервале частот ![]() положительна, тогда как
положительна, тогда как ![]() ниже
ниже ![]() положительна,
а выше – отрицательна. Однако теперь на любых частотах всегда абсолютная величина
положительна,
а выше – отрицательна. Однако теперь на любых частотах всегда абсолютная величина
![]() превышает абсолютную величину
превышает абсолютную величину ![]() , в результате чего разность квадратов
, в результате чего разность квадратов ![]() , присутствующая в числителе выражения для
, присутствующая в числителе выражения для
![]() (116), всегда положительна. При этом, с
учетом того, что в рассматриваемом случае проницаемость
(116), всегда положительна. При этом, с
учетом того, что в рассматриваемом случае проницаемость ![]() всегда
положительна, параметр
всегда
положительна, параметр ![]() , в соответствии с (116), также
всегда является положительным, как это видно из рис.8б.
, в соответствии с (116), также
всегда является положительным, как это видно из рис.8б.
Это означает, что для волнового числа и адмиттанса запрещенных областей нет, то есть волна может существовать во всем интервале частот от минус до плюс бесконечности.
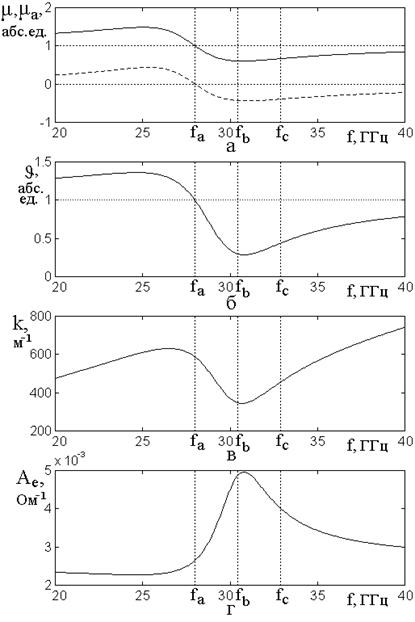
Рис.8. Частотные зависимости
характерных параметров распространения волны при сильном затухании: ![]() .
.
Все обозначения и остальные параметры – те же, что на рис.6.
Поведение волнового числа и
адмиттанса в этом случае иллюстрируется рис.8в и рис.8г соответственно. Видно,
что оба эти параметра между частотами ![]() и
и ![]() хотя и испытывают изменение знака
производной, приводящее к наличию экстремумов, но существуют во всех точках
шкалы частот, не имея ни нулей, ни каких-либо особенностей и тем более
расходимостей.
хотя и испытывают изменение знака
производной, приводящее к наличию экстремумов, но существуют во всех точках
шкалы частот, не имея ни нулей, ни каких-либо особенностей и тем более
расходимостей.
Таким образом, можно сделать вывод, что при сильном затухании волна в магнитной среде может распространяться при любых частотах.
ЗАМЕЧАНИЕ.
В ходе проведенного рассмотрения на основе отрицательности параметра
расходимости (116) сделан вывод о невозможности распространения волны в таких
условиях. Однако, как можно видеть из аналитических выражений для волнового
числа (49) и адмиттанса (56), при отрицательной величине ![]() алгебраическое вычисление корня приводит
к комплексным выражениям. Вообще говоря, комплексное волновое число означает не
просто отсутствие волны, а ее постепенное затухание по пути распространения. Можно
полагать, что то же относится к адмиттансу. То есть волна на входе в участок среды
с отрицательным значением
алгебраическое вычисление корня приводит
к комплексным выражениям. Вообще говоря, комплексное волновое число означает не
просто отсутствие волны, а ее постепенное затухание по пути распространения. Можно
полагать, что то же относится к адмиттансу. То есть волна на входе в участок среды
с отрицательным значением ![]() продолжает
распространяться с амплитудой, падающей по экспоненциальному закону. То есть
происходит что-то подобное входу волны в запредельный волновод [23-29]. При
этом волна на выходе из такого участка будет иметь амплитуду значительно
меньшую входной. Прямые свойства прецессии намагниченности, по-видимому,
задействованы не будут, то есть волна будет распространяться как в диэлектрике
без намагниченности. Такое поведение волны требует отдельного рассмотрения и в
настоящий момент выходит за рамки нашей работы.
продолжает
распространяться с амплитудой, падающей по экспоненциальному закону. То есть
происходит что-то подобное входу волны в запредельный волновод [23-29]. При
этом волна на выходе из такого участка будет иметь амплитуду значительно
меньшую входной. Прямые свойства прецессии намагниченности, по-видимому,
задействованы не будут, то есть волна будет распространяться как в диэлектрике
без намагниченности. Такое поведение волны требует отдельного рассмотрения и в
настоящий момент выходит за рамки нашей работы.
20. Распределение амплитуд
Рассмотрим теперь распределение амплитуд волн при тензорной магнитной проницаемости барьеров для различных частот. Ограничимся волнами прямого направления, так как проведенное предварительное исследование показало, что волны обратного направления ведут себя подобным же образом, как это имеет место для диэлектриков [2]. Будем рассматривать сильное различие параметров барьеров и промежутков, чтобы яснее выявить характерные особенности. Ограничимся рассмотрением только случаев слабого и сильного затухания, так как в них отражены уже наиболее характерные особенности распределения волн, а случай среднего затухания является промежуточным.
Обратимся к рис.9, где показано распределение амплитуд волн прямого направления в слоях структуры при тензорной магнитной проницаемости барьеров для различных частот.
Рис.9а,б,в (левый
столбец) соответствует случаю слабого затухания (![]() ), рис.9г,д,е
– сильного (
), рис.9г,д,е
– сильного (![]() ). Частоты возбуждения выбраны следующим
образом. Для рис.9а и 9г частота
). Частоты возбуждения выбраны следующим
образом. Для рис.9а и 9г частота ![]() располагается несколько
ниже частоты
располагается несколько
ниже частоты ![]() , соответствующей началу зоны запрещения,
для рис.9в и 9е частота
, соответствующей началу зоны запрещения,
для рис.9в и 9е частота ![]() располагается несколько
выше значения
располагается несколько
выше значения ![]() , соответствующего окончанию
зоны запрещения. То есть эти частоты, находясь в пределах зоны разрешения, охватывают
зону запрещения в непосредственной близости с обеих сторон. Частота
, соответствующего окончанию
зоны запрещения. То есть эти частоты, находясь в пределах зоны разрешения, охватывают
зону запрещения в непосредственной близости с обеих сторон. Частота ![]() , соответствующая рис.9б, приходится на
середину участка, разрешенного при слабом затухании, то есть между
, соответствующая рис.9б, приходится на
середину участка, разрешенного при слабом затухании, то есть между ![]() и
и ![]() . Напомним,
что в этом случае адмиттанс является отрицательным. Частота
. Напомним,
что в этом случае адмиттанс является отрицательным. Частота ![]() , соответствующая рис.9д, приходится на
середину участка, запрещенного при слабом затухании, но разрешенного при
сильном, то есть между
, соответствующая рис.9д, приходится на
середину участка, запрещенного при слабом затухании, но разрешенного при
сильном, то есть между ![]() и
и ![]() . Таким
образом, можно полагать, что здесь охвачены все возможные случаи частот,
соответствующих различным условиям распространения волн.
. Таким
образом, можно полагать, что здесь охвачены все возможные случаи частот,
соответствующих различным условиям распространения волн.
Из рисунка видно, что при всех рассмотренных случаях наблюдаются все те же распределения амплитуд, что и в случае диэлектрической среды [2]. Так рис.9б,в,г,д соответствуют синусоидальному распределению, рис.9а – полусинусоидальному, рис.9д – экспоненциальному.
Из сравнения пар рисунков в горизонтальных рядах, то есть 9а с 9г, 9б с 9д и 9в с 9д можно видеть, что при увеличении параметра затухания амплитуды во всех слоях в общем уменьшаются.
Однако из рисунков, соответствующих синусоидальным распределениям (9б,в,г,д), можно видеть, что при удалении от начала структуры, то есть при возрастании номеров слоев, общий размах амплитуд в соседствующих или последовательных близко расположенных слоях не уменьшается ни при слабом, ни при сильном затухании. Особенно хорошо это видно из рис.9в, где размах амплитуд между слоями №3 и №4 в точности равен размаху амплитуд между слоями №11 и №12 или размах между более удаленными слоями №3 и №6 также равняется размаху между слоями №11 и №14. Аналогичные закономерности легко прослеживаются также из рис.9г, например при сравнении слоев №7 с №8 или №13 с №14.
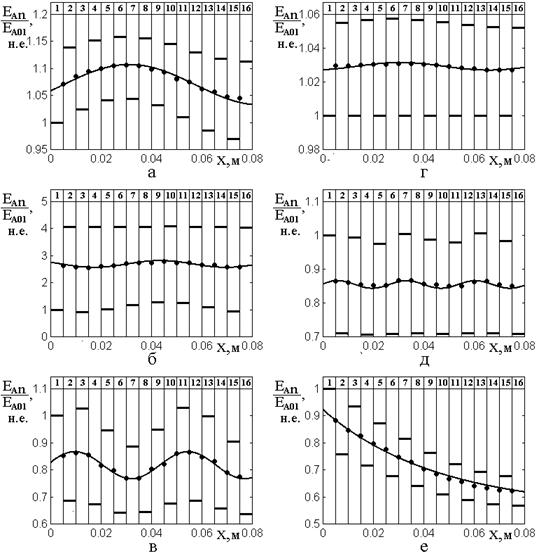
Рис.9. Распределение амплитуд волн
прямого направления при тензорной магнитной проницаемости барьеров для
различных частот и параметров магнитного затухания. ![]() ;
; ![]() .
. ![]() ;
; ![]() – определяется формулой (107) с учетом
(108)-(109). Параметр затухания: а,б,в –
– определяется формулой (107) с учетом
(108)-(109). Параметр затухания: а,б,в – ![]() ;
г,д,е –
;
г,д,е – ![]() . Частоты: а,г –
. Частоты: а,г – ![]() ;
б –
;
б – ![]() ; д –
; д – ![]() ; в,е
–
; в,е
– ![]() . Остальные параметры – те же что на
предыдущих рисунках.
. Остальные параметры – те же что на
предыдущих рисунках.
Таким образом, можно сделать вывод, что магнитное затухание не приводит к абсолютному затуханию волны по координате, а действует как реактивный параметр, определяя амплитуду лишь в каждом отдельном слое по всей его длине, не меняя амплитуды в соседних слоях. То есть затухание определяет лишь размах и максимальную амплитуду колебаний в соответствующих слоях, а поток энергии, входящий в слой и выходящий из него, остается постоянным.
ЗАМЕЧАНИЕ. Отмеченное здесь отсутствие затухания гиромагнитной волны по координате, несмотря на наличие магнитного затухания в каждом слое, на первый взгляд кажется парадоксальным, однако оно обусловлено неучетом уменьшения амплитуды волны при распространении в среде с потерями. Действительно, здесь магнитные колебания в каждом отдельном слое предполагаются однородными, то есть их амплитуда на обоих границах слоя остается одной и той же. Такое рассмотрение правомерно только в случае достаточно тонких слоев, когда падение амплитуды по толщине слоя незначительно. Критерий такой правомерности должен определяться отдельно для каждой конкретной задачи. В более корректном варианте следует учитывать затухание волны при распространении внутри каждого данного слоя подобно тому, как это сделано в работе [19-22].
21. Баланс потоков энергии
Несколько неожиданным выглядит заметное увеличение амплитуды колебаний на рис.9б, где частота выбрана в интервале, где адмиттанс является отрицательным. Вообще говоря, из аналогии с электротехникой, импеданс представляет собой как бы сопротивление волноведущей среды, тогда как адмиттанс – проводимость. При этом отрицательное сопротивление означает приток энергии в систему в противоположность ее оттоку при сопротивлении положительном. Следуя подобной логике можно полагать, что отрицательный адмиттанс также соответствует притоку энергии, что нарушает закон ее сохранения.
Амплитуда волн обратного
направления в условиях рис.9б также велика, так для волн прямого направления
размах амплитуды в соседствующих слоях составляет от ![]() до
до
![]() , а для волн обратного направления – от
, а для волн обратного направления – от ![]() до
до ![]() То
есть энергия как бы притекает к волнам как того, так и другого направления.
То
есть энергия как бы притекает к волнам как того, так и другого направления.
Для разрешения этого парадокса
рассмотрим потоки энергии в структуре по отдельности. Прежде всего отметим, что
поток энергии волн прямого направления ориентирован в положительном направлении
оси ![]() (то есть по рисунку слева направо), тогда
как поток энергии волн обратного направления ориентирован в отрицательном направлении
той же оси (по рисунку справа налево).
(то есть по рисунку слева направо), тогда
как поток энергии волн обратного направления ориентирован в отрицательном направлении
той же оси (по рисунку справа налево).
При этом в структуру в слое №1 входит один поток – падающий, а выходит два – отраженный в том же слое №1 и проходящий в слое №16. То есть в структуре в целом должен выполняться баланс потоков энергии следующего вида:
где ![]() –
поток энергии падающей волны (прямого направления) в слое №1,
–
поток энергии падающей волны (прямого направления) в слое №1, ![]() – поток энергии отраженной волны
(обратного направления) в слое №1,
– поток энергии отраженной волны
(обратного направления) в слое №1, ![]() – поток энергии
проходящей волны (прямого направления) в слое №16.
– поток энергии
проходящей волны (прямого направления) в слое №16.
Следуя приведенным в работе [2] правилам перехода от одномерной волны к электромагнитной, а также учитывая определение потока энергии для одномерной волны [19-22], получаем потоки энергии распространяющихся волн в виде:
поток энергии, входящий в структуру за счет падающей волны, равен:
![]() ;
(118)
;
(118)
поток энергии, выходящий из структуры за счет отраженной волны:
![]() ;
(119)
;
(119)
поток энергии, выходящий из структуры за счет проходящей волны:
![]() .
(120)
.
(120)
Рассмотрим теперь численные соотношения потоков энергии в случае положительного и отрицательного адмиттанса.
Так на частоте ![]() , где адмиттанс положителен, получаем амплитуды
полей:
, где адмиттанс положителен, получаем амплитуды
полей: ![]() ,
, ![]() ,
, ![]() ,
, ![]() При
этом адмиттансы равны:
При
этом адмиттансы равны: ![]() ;
; ![]() . Подставляя в (118)-(120) приведенные
выше числовые значения амплитуд полей и адмиттансов, получаем:
. Подставляя в (118)-(120) приведенные
выше числовые значения амплитуд полей и адмиттансов, получаем: ![]() ,
, ![]() ,
, ![]()
Легко проверить, что при таких численных значениях условие (117) выполняется.
На частоте ![]() , где адмиттанс отрицателен, амплитуды
полей и адмиттансы соответственно равны:
, где адмиттанс отрицателен, амплитуды
полей и адмиттансы соответственно равны:
![]() ,
, ![]() ,
,
![]() ,
, ![]()
При этом адмиттансы равны:
![]() ;
; ![]() .
.
Потоки энергии при таких численных
значениях получаются равными: ![]() ,
,
![]() ,
,
![]()
Можно видеть, что и при этих численных значениях условие (117) также выполняется.
Таким образом, можно сделать вывод, что условие баланса энергии на структуре в целом выполняется при любых, как положительных, так и отрицательных значениях адмиттанса.
При этом вопрос о
чрезмерном на первый взгляд увеличении амплитуды волн в случае отрицательного
импеданса в этом случае математически решается, однако физический смысл
отрицательного значения потока энергии ![]() ,
проходящего через структуру, по-видимому, состоит в изменении его направления в
соответствии с отрицательным знаком. То есть можно полагать, что здесь имеет
место аналогия с распространением обратной волны, в которой направления фазовой
и групповой скоростей противоположны [32-38]. Увеличение же амплитуды волн во
внутренних слоях структуры по сравнению с амплитудой падающей волны можно
трактовать как переход волны из среды более плотной в среду менее плотную
(аналогично отмеченному в разделе №5).
,
проходящего через структуру, по-видимому, состоит в изменении его направления в
соответствии с отрицательным знаком. То есть можно полагать, что здесь имеет
место аналогия с распространением обратной волны, в которой направления фазовой
и групповой скоростей противоположны [32-38]. Увеличение же амплитуды волн во
внутренних слоях структуры по сравнению с амплитудой падающей волны можно
трактовать как переход волны из среды более плотной в среду менее плотную
(аналогично отмеченному в разделе №5).
ЗАМЕЧАНИЕ.
Использованное здесь определение потока энергии как произведения квадрата
амплитуды электрического поля на адмиттанс среды, полученное из аналогии с
одномерной волной, вообще говоря, относится к потоку, распространяющемуся точно
вдоль оси структуры, то есть вдоль оси ![]() на
рис.1, 4, 5. Для изотропного диэлектрика такое определение соответствует
классическому определению потока энергии через вектор Пойнтинга [23-29]. При
этом предполагается, что магнитное поле волны перпендикулярно электрическому и
по абсолютной величине равно произведению электрического поля на адмиттанс
среды. Однако для гиромагнитной волны магнитное поле кроме поперечной имеет
также и продольную составляющую, в результате чего вектор Пойнтинга за счет
входящего в него векторного произведения отклоняется от оси структуры, приобретая
составляющую вдоль оси
на
рис.1, 4, 5. Для изотропного диэлектрика такое определение соответствует
классическому определению потока энергии через вектор Пойнтинга [23-29]. При
этом предполагается, что магнитное поле волны перпендикулярно электрическому и
по абсолютной величине равно произведению электрического поля на адмиттанс
среды. Однако для гиромагнитной волны магнитное поле кроме поперечной имеет
также и продольную составляющую, в результате чего вектор Пойнтинга за счет
входящего в него векторного произведения отклоняется от оси структуры, приобретая
составляющую вдоль оси ![]() . В настоящей работе мы полагаем
структуру в плоскости
. В настоящей работе мы полагаем
структуру в плоскости ![]() бесконечно протяженной, поэтому
такую составляющую не рассматриваем.
бесконечно протяженной, поэтому
такую составляющую не рассматриваем.
22. Отражение и прохождение в широком диапазоне частот
Рассмотрим теперь частотные зависимости амплитуд волн в слоях в более широком диапазоне частот, когда характеристики отражения и прохождения определяются как магнитным, так и геометрическим факторами структуры.
Как показано в разделах №17,18,
при слабом и среднем магнитном затухании в диапазоне частот появляются
запрещение полосы, где распространение электромагнитных волн невозможно.
Поэтому можно ожидать, что на общем частотном спектре отражения и прохождения,
подобном показанному в работе [2] на рис.6, появятся какие-то провалы,
обусловленные упомянутыми полосами запрещения. Более подробное исследование
показывает, что на обоих краях таких провалов со стороны разрешенных частот
отражение волн стремится к единице, а прохождение – к нулю. В остальных частях
разрешенных областей отражение и прохождение определяется конкретными
значениями компонент магнитной проницаемости, которые для ![]() близки к единице, а для
близки к единице, а для ![]() – к нулю. То есть картина распространения
волн мало отличается от случая скалярной магнитной проницаемости, причем при
сравнительно небольших ее значениях.
– к нулю. То есть картина распространения
волн мало отличается от случая скалярной магнитной проницаемости, причем при
сравнительно небольших ее значениях.
С другой стороны, как показано в тех же разделах, при сильном магнитном затухании запрещенные области отсутствуют, так что волна может распространяться во всем интервале частот от нуля до плюс бесконечности (разумеется, в тех пределах, где работают обычные механизмы прецессии намагниченности в гиротропной среде [7-9]). Поэтому дальнейшее рассмотрение посвятим именно случаю сильного магнитного затухания и рассмотрим трансформацию амплитуд в слоях в широком диапазоне частот.
Обратимся к рис.10, где
показаны зависимости нормированных амплитуд обратно направленной волны в слое
№1 (а,б) и прямо направленных волн в слоях №15 (в) и №16 (г) от частоты
падающей волны при двух различных значениях намагниченности. На рисунке
вертикальными пунктирными линиями показаны граничные частоты запрещенной
области, то есть ![]() и
и ![]() ,
определяемые формулами (113) и (115), равные соответственно
,
определяемые формулами (113) и (115), равные соответственно ![]() и
и ![]() . Вертикальными
точечными линиями показаны частоты, определяемые укладыванием нечетного числа
четвертей длин волн на длине одного барьера. Для расчета таких частот в работе
[2] предложены две формулы, первая – аналитическая под номером (65):
. Вертикальными
точечными линиями показаны частоты, определяемые укладыванием нечетного числа
четвертей длин волн на длине одного барьера. Для расчета таких частот в работе
[2] предложены две формулы, первая – аналитическая под номером (65):
где ![]() –
порядковый номер максимума, при котором на длине барьера укладывается
–
порядковый номер максимума, при котором на длине барьера укладывается ![]() четвертей длин волн,
четвертей длин волн, ![]() – скорость электромагнитной волны в
свободном пространстве (
– скорость электромагнитной волны в
свободном пространстве (![]() );
);
вторая – эмпирическая под номером (66):
где полагается ![]() .
.
В рассматриваемом случае
вертикальные точечные линии построены по формуле (121) при ![]() (частота
(частота ![]() ) и при
) и при
![]() (частота
(частота ![]() ).
).
В дальнейших расчетах
полагаем параметр затухания ![]() , то есть, в соответствии
с приведенной в разделе №5 оценкой, затухание является сильным.
, то есть, в соответствии
с приведенной в разделе №5 оценкой, затухание является сильным.
Итак
переходим к рассмотрению рисунка. Случай рис.10а соответствует крайне малой
намагниченности барьеров, равной ![]() , то есть можно
считать, что при этом
, то есть можно
считать, что при этом ![]() ,
, ![]() . Этот
случай приведен здесь для сравнения. Показана амплитуда только волны обратного
направления в слое №1, при этом амплитуды волн прямого направления в слоях №15
и №16 равны единице с точностью до
. Этот
случай приведен здесь для сравнения. Показана амплитуда только волны обратного
направления в слое №1, при этом амплитуды волн прямого направления в слоях №15
и №16 равны единице с точностью до ![]() То есть можно считать,
что от структуры практически ничего не отражается, а вся энергия возбуждаемых
волн проходит насквозь. Однако, тем не менее, на частотной характеристике четко
выражены два максимума при частотах
То есть можно считать,
что от структуры практически ничего не отражается, а вся энергия возбуждаемых
волн проходит насквозь. Однако, тем не менее, на частотной характеристике четко
выражены два максимума при частотах ![]() и
и ![]() . Таким образом, даже при столь малой
намагниченности, весьма далекой от условий магнитного резонанса, геометрические
резонансные свойства магнитных барьеров, хотя и крайне слабо, но все же
проявляются, давая четко выраженные максимумы отражения на частотах, практически
точно соответствующих укладыванию нечетного числа четвертей длин волн по длине
магнитного барьера (121). В интервале частот, соответствующем полосе непропускания
(между пунктирными линиями) каких-либо особенностей не наблюдается.
. Таким образом, даже при столь малой
намагниченности, весьма далекой от условий магнитного резонанса, геометрические
резонансные свойства магнитных барьеров, хотя и крайне слабо, но все же
проявляются, давая четко выраженные максимумы отражения на частотах, практически
точно соответствующих укладыванию нечетного числа четвертей длин волн по длине
магнитного барьера (121). В интервале частот, соответствующем полосе непропускания
(между пунктирными линиями) каких-либо особенностей не наблюдается.

Рис.10. Зависимости нормированных амплитуд обратно направленной волны в слое №1 (а,б) и прямо направленных волн в слоях №15 (в) и №16 (г) от частоты падающей волны при двух различных значениях намагниченности.
а – ![]() ; б,в,г
–
; б,в,г
– ![]() .
.
Компоненты магнитной проницаемости определяются формулами (107)-(109).
Другие параметры: ![]() ,
, ![]() ,
, ![]() .
.
Остальные параметры – те же, что на предыдущих рисунках.
Случай выполнения условий
магнитного резонанса представлен на рис.10б,в,г. Здесь, во-первых, представлены
те же две резонансные линии, которые определяются геометрией барьера. Однако
частоты обеих резонансных линий несколько раздвинуты в разные стороны:
низкочастотная отодвинута вниз на частоту ![]() , а
высокочастотная – вверх на частоту
, а
высокочастотная – вверх на частоту ![]() .
.
Таким образом, если можно считать снижение частоты линии первого максимума в какой-то степени соответствующим формуле (122), то относительно второго максимума этого сказать нельзя, так как он смещается не вниз, а вверх. Причиной такого смещения вверх второго максимума можно считать влияние магнитных свойств среды.
В то же время, в области
магнитного резонанса здесь возникает новая довольно широкая линия
(соответствующие этой линии участки кривых выделены утолщенными линиями).
Нижний край этой линии приходится на частоту ![]() , то
есть в точности совпадает с частотой
, то
есть в точности совпадает с частотой ![]() , а верхний – на частоту
, а верхний – на частоту
![]() , что заметно превышает частоту
, что заметно превышает частоту ![]() . Более того, резко выраженный максимум
этой линии приходится на частоту
. Более того, резко выраженный максимум
этой линии приходится на частоту ![]() , что также превышает
, что также превышает ![]() . Таким образом, хотя основная часть
линии, обусловленной резонансными свойствами магнитной среды совпадает с
интервалом между характерными частотами
. Таким образом, хотя основная часть
линии, обусловленной резонансными свойствами магнитной среды совпадает с
интервалом между характерными частотами ![]() и
и ![]() , наиболее резкий максимум этой линии располагается
уже за пределами характерного интервала. На частотных зависимостях прохождения
(рис.10в и 10г) обособление максимума на частоте
, наиболее резкий максимум этой линии располагается
уже за пределами характерного интервала. На частотных зависимостях прохождения
(рис.10в и 10г) обособление максимума на частоте ![]() выражено
еще сильнее, чем на зависимостях отражения (рис.10б).
выражено
еще сильнее, чем на зависимостях отражения (рис.10б).
Причина появления такого
максимума, по-видимому, кроется в том, что, как можно видеть из рис.8,
адмиттанс при частотах в ближней окрестности выше ![]() снижается
незначительно (в рассмотренном на рис.8 интервале не более чем на 30%), а
волновое число в том же интервале увеличивается почти в три раза. Можно
полагать, что при этом слагаемые, составляющие детерминанты, которые определяют
амплитуды волн в соответствии с пошаговым алгоритмом [2], увеличиваются в такой
степени, что и дают в результате не только смещение основного максимума рассматриваемой
линии вверх по частоте, но и некоторый выход его за пределы частоты
снижается
незначительно (в рассмотренном на рис.8 интервале не более чем на 30%), а
волновое число в том же интервале увеличивается почти в три раза. Можно
полагать, что при этом слагаемые, составляющие детерминанты, которые определяют
амплитуды волн в соответствии с пошаговым алгоритмом [2], увеличиваются в такой
степени, что и дают в результате не только смещение основного максимума рассматриваемой
линии вверх по частоте, но и некоторый выход его за пределы частоты ![]() .
.
Заметим дополнительно, что из рис.10г видно, что амплитуда прямо направленной волны в слое №16 превышает единицу, то есть здесь происходит переход волны из более плотной среды в менее плотную. Таким образом, можно считать, что увеличение гиромагнитных свойств среды, то есть увеличение ее магнитной проницаемости, приводят к уменьшению ее плотности по отношению к распространению электромагнитных волн. Такое обстоятельство находится в обратном соотношении с диэлектрическими свойствами, где, как показано в работе [2], увеличение диэлектрической проницаемости приводит для плотности диэлектрической среды к ее увеличению. В разделе №5 подобное обратное соотношение роли той и другой проницаемостей уже отмечалось для случая скалярной магнитной проницаемости, здесь же оно дополнительно подтверждено для проницаемости тензорной.
Заключение
Рассмотрено распространение электромагнитных волн прямого и обратного направлений в многослойной структуре ограниченной длины с периодической неоднородностью меандрового типа, барьеры которой обладают магнитодиэлектрическими свойствами. В качестве расчетного аппарата использован метод пошагового алгоритма, обобщенный на случай трехмерных электромагнитных волн, распространяющихся в среде с магнитными параметрами.
Для случая скалярной магнитной проницаемости получены те же закономерности распространения волн, что и для изотропной диэлектрической среды с тем отличием, что повышение диэлектрической проницаемости среды приводит к повышению ее электродинамической плотности, тогда как увеличение магнитной проницаемости такую плотность уменьшает.
Распределение амплитуд волн в отдельных слоях структуры подобно таковому для случая диэлектрической среды, то есть наблюдаются те же два основных вида распределения – синусоидальное и экспоненциальное, а также два переходных – полусинусоидальное и линейное.
В качестве предварительного этапа для изучения тензорных сред рассмотрено распространение электромагнитной волны в бигиротропной среде с общей осью гиротропии для магнитной и диэлектрической проницаемостей. Показано, что в такой среде перпендикулярно оси гиротропии возможно распространение двух независимых друг от друга волн – гиромагнитной и гироэлектрической, каждая из которых кроме поперечных составляющих полей имеет также и продольные, причем в случае образования гиротропии за счет постоянного магнитного поля решающую роль играет гиромагнитная волна.
Рассмотрено отражение и прохождение гиромагнитной волны при падении на плоскую границу раздела двух сред с магнитными параметрами. Получены амплитуды отраженной и проходящей волн, выраженные через адмиттансы сред, образованные совокупностью компонент соответствующих тензоров магнитной проницаемости. Получены два вида адмиттансов – линейномагнитный и гиромагнитный, каждый из которых ответственен за свои компоненты полей распространяющихся волн. На основе механизма прецессии вектора намагниченности в среде с магнитными потерями рассчитаны компоненты гиротропного тензора магнитной проницаемости, а также линейномагнитный и гиромагнитный адмиттансы среды.
Введен в рассмотрение «параметр расходимости», представляющий собой комбинацию из компонент тензора, определяющий частотные области существования действительных адмиттансов, а также волновых чисел распространяющихся волн. Показано, что в многослойной структуре с тензорными параметрами имеются области частот, где распространение волн невозможно, что определяются отрицательным знаком параметра расходимости. Найдены три характерные частоты, определяющие границы упомянутых областей, выявлена их зависимость от намагниченности среды и величины создающего гиротропию магнитного поля.
По величине параметра затухания магнитных колебаний выделены три характерных области: слабого, среднего и сильного затухания. Показано, что в случае слабого затухания в области частот между двумя крайними характерными значениями распространение гиромагнитных волн запрещено, тогда как вне этой области – возможно. В случае сильного затухания какие-либо запрещения для распространения гиромагнитных волн отсутствуют.
Для распределения амплитуд волн в отдельных слоях структуры для тензорной среды наблюдаются те же его виды, что и для скалярной среды – основные синусоидальное и экспоненциальное, а также переходные – полусинусоидальное и линейное.
Отмечено аномально большое (в два-три раза) увеличение амплитуды волн прямого и обратного направления в области частот, где линейномагнитный адмиттанс является отрицательным. Для интерпретации этого случая рассмотрен баланс потоков энергии распространяющихся волн на структуре в целом. Показано, что несмотря на отрицательность адмиттанса баланс энергии в этом случае выполняется в той же степени, как и при положительном значении адмиттанса. Наблюдаемое увеличение амплитуды отнесено к ситуации распространения волны из области более плотной в область менее плотную, аналогичной таковой для скалярной проницаемости.
В широком диапазоне рассмотрена частотная зависимость амплитуд волн обоих направлений в крайних и некоторых промежуточных слоях структуры. Показано, что даже в случае намагниченности на четыре-пять порядков ниже соответствующей реальным магнитным средам, амплитуда отраженной волны имеет те же резонансные особенности, соответствующие укладыванию по длине одного барьера нечетного числа четвертей длин волн, что и для диэлектрика. Однако при реальных значениях намагниченности кроме этих резонансов появляется широкая дополнительная линия, обусловленная именно магнитными свойствами среды. Общее положение этой линии задается характерными частотами, определяющими знак параметра расходимости, однако максимум приходится на частоту несколько выше наибольшей из характерных частот, что обусловлено медленностью спада адмиттанса и ростом волнового числа в этой области.
Работа выполнена при финансовой поддержке за счет гранта Российского Научного Фонда (проект № 14-22-00279).
Литература
1. Антонец И.В., Шавров В.Г., Щеглов В.И. // Журнал радиоэлектроники [электронный журнал]. 2015. №2. URL: http://jre.cplire.ru/jre/feb15/1/text.html (первая часть настоящей работы).
2. Антонец И.В., Шавров В.Г., Щеглов В.И. // Журнал радиоэлектроники [электронный журнал]. 2015. №2. URL: http://jre.cplire.ru/jre/feb15/2/text.html (вторая часть настоящей работы).
3. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2012. Т.57. №1. С.67.
4. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2013. Т.58. №1. С.16.
5. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Журнал радиоэлектроники [электронный журнал]. 2013. №1. URL:
http://jre.cplire.ru/jre/jan13/11/text.pdf.
6. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры (монография). Часть пятая. Алгоритмические методы. Сыктывкар: ИПО СыктГУ. 2014.
7. Гуревич А.Г. Ферриты на сверхвысоких частотах. М.: Гос.Изд.физ.-мат.лит. 1960.
8. Гуревич А.Г. Магнитный резонанс в ферритах и антиферромагнетиках. М.: Наука. 1973.
9. Гуревич А.Г., Мелков Г.А. Магнитные колебания и волны. М.: Физматлит. 1994.
10. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Сборник трудов XXI Международной конференции “Новое в магнетизме и магнитных материалах (НМММ)”. Москва: МГУ. 2009. С.939.
11. Зубков В.И., Щеглов В.И. // РЭ. 2002. Т.47. №9. С.1101.
12. Зубков В.И., Щеглов В.И. // РЭ. 2003. Т.48. №10. С.1186.
13. Зубков В.И., Щеглов В.И. // Сборник трудов XIX Международной конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2011. С.245.
14. Зубков В.И., Щеглов В.И. // Сборник трудов XX Международной конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2012. С.260.
15. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2012. Т.57. №1. С.67.
16. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2013. Т.58. №1. С.16.
17. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Журнал радиоэлектроники [электронный журнал]. 2013. №1. URL:
http://jre.cplire.ru/jre/jan13/11/text.pdf.
18. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры (монография). Часть пятая. Алгоритмические методы. Сыктывкар: ИПО СыктГУ. 2014.
19. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2009. Т.54. №10. С.1171.
20. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Сборник трудов XVI Международной конференции "Радиолокация и радиосвязь". Москва: НИУ МЭИ. 2008. С.18.
21. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Сборник трудов XIX Международной конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2011. С.166.
22. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Сборник трудов XX Международной конференции «Электромагнитное поле и материалы». Москва: «НИУ МЭИ». 2012. С.215.
23. Семенов А.А. Теория электромагнитных волн. М.: Изд.МГУ. 1968.
24. Никольский В.В, Никольская Т.И. Электродинамика и распространение радиоволн. М.: Наука. 1989.
25. Красюк Н.П., Дымович Н.Д. Электродинамика и распространение радиоволн. М.: Высшая школа. 1974.
26. Ионкин П.А., Мельников Н.А., Даревский А.И., Кухаркин Е.С. Теоретические основы электротехники. Часть 1. Основы теории цепей. М.: Высшая школа. 1965.
27. Даревский А.И., Кухаркин Е.С. Теоретические основы электротехники. Часть 2. Основы теории электромагнитного поля. М.: Высшая школа. 1965.
28. Вайнштейн Л.А. Электромагнитные волны. М.: Сов. радио. 1957.
29. Вайнштейн Л.А. Электромагнитные волны. М.: Радио и связь. 1988.
30. Чертов А.Г. Единицы физических величин. М.: Высшая школа. 1977.
31. Сена Л.А. Единицы физических величин и их размерности. М.: Наука. 1977.
32. Шустер А. Введение в теоретическую оптику. М.-Л.: ОНТИ. 1935.
33. Веселаго В.Г. // УФН. 1967. Т.92. №3. С.517.
34. Pendry J.B. // Phys. Rev. Lett. 2000. V.85. P.3966.
35. Виноградов А.П. Электродинамика композитных материалов. М.: УРСС. 2001.
36. Шевченко В.В. // УФН. 2004. Т.177. №1. С.301.
37. Агранович В.М., Гартштейн Ю.Н. // УФН. 2006. Т.176. №10. С.1052.