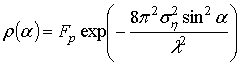УДК 621.396.62

МОДЕЛЬ ПАССИВНОЙ ПОМЕХИ ПРИ РАДИОЛОКАЦИИ НИЗКОВЫСОТНЫХ ЦЕЛЕЙ НАД МОРСКОЙ ПОВЕРХНОСТЬЮ

 

А. Н. Пинчук

Черноморское высшее военно-морское училище им. П.С. Нахимова

 

Статья получена 12 января 2015 г., после доработки – 7 марта 2015 г.

 

Аннотация. Методом математического моделирования исследуется влияние метеоусловий, в частности скорости ветра, на параметры сигнала, отраженного морской поверхностью, при радиолокации низковысотных целей. Приведены основные математические соотношения для расчета интенсивности пассивной помехи, обусловленной отражением от взволнованной морской поверхности, при различных метеоусловиях.

Ключевые слова: метеоусловия, низковысотная радиолокационная цель, отражение от морской поверхности, пассивная помеха.

Abstract. Influence of meteoconditions, particularly wind speed, on parameters of signal reflected by sea surface in the case of low-height target radar sounding is studied using mathematical modeling. Basic formulae for calculation of intensity of the passive interference caused by reflection from excited sea surface for various meteoconditions are presented.

Key words: low-height radar target, meteoconditions, passive interference, sea return.

Введение

Радиолокационное обнаружение, сопровождение и распознавание кораблей, а также низколетящих целей, требует учета взаимодействия радиоволн с морской поверхностью [1,2]. Сигнал, отраженный от цели, маскируется пассивной помехой, структура которой в результате переотражений электромагнитного излучения от возмущенной поверхности моря, во многом определяет эффективность работы прибрежных и бортовых РЛС.

Сложность учета характеристик таких помех при селекции целей связана с сильной изменчивостью структуры поверхности. Не смотря на многолетние исследования в этой области [3,4], тонкая топографическая структура границы океан-атмосфера, формируемая короткими поверхностными волнами, до настоящего времени остается недостаточно изученной [5].

В настоящее время в России и за рубежом ведутся интенсивные теоретические и экспериментальные исследования физических механизмов формирования радиосигналов, отраженных от морской поверхности [6-8]. Показана заметная роль нелинейных процессов в поле поверхностных волн, которые приводят к отклонению статистических распределений возвышений морской поверхности и ее уклонов от распределения Гаусса [9], а также процессов, связанные с обрушением волн [10].

Отражения от морской поверхности создают помехи как при прямом, так и обратном прохождения радиоволн от РЛС. В представленной работе проводится анализ характеристик помех, возникающих при прямом прохождении. Этот случай можно рассматривать, как двухпозиционное зондирование, при котором основной вклад в формирование эхо-сигнала дает механизм зеркального отражения [11].

Двухпозиционное зондирование

Рассмотрим ситуацию, когда РЛС, расположенная на высоте , облучает цель, находящуюся на высоте  и проанализируем сигнал , регистрируемый на этой цели. Наличие области зеркального отражения на морской поверхности и двухлучевое распространение радиоволн в основном луче РЛС делает правомерной постановку задачи двухпозиционного зондирования.

При взаимодействии радиоволн с морской поверхностью отраженный от нее сигнал формируют два основных физических механизма: зеркальное отражение и резонансное рассеяние. Будем полагать, что РЛС работает в сантиметровом диапазоне. Рассмотрим критерий Рэлея

,                                                           (1)

 

где  – длина радиоволны;  – стандартное отклонение высот морской поверхности;  – угол скольжения. Если , то поверхность считается “гладкой” и преобладает механизм зеркального отражения [4]. В частности, при углах скольжения до 2º и длине радиоволны 3 см, механизм зеркального отражения будет преобладать, если выполняется условие 10 см.

Результирующий эхо-сигнал  является суммой двух составляющих: сигнала, напрямую попавшего на цель, и сигнала, переотразившегося от морской поверхности в направлении цели. Морская поверхность не является плоской. Она возмущена волнами, меняющими ее локальные уклоны и, следовательно, область, где существуют точки переотражениий. Присутствие волн, удовлетворяющих условию (1), определяет протяженность этой области, от которой происходит зеркальное отражение радиоволн в направлении цели.

 

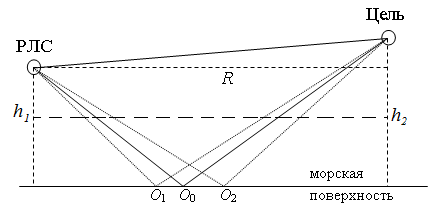
Рис. 1. Схематичное изображение радиолокационного облучения  надводной цели

 

Из простых геометрических построений несложно получить условие для угла скольжения (отсчитываемого от горизонтали), при котором имеет место зеркальное отражение радиоволн от плоской поверхности в направлении цели (см. рис. 1)

,                                                    (2)

 

где  и  – высота РЛС и цели над невозмущенной морской поверхностью соответственно;  – угол скольжения, отсчитываемый от горизонтали;  – расстояние между точками, соответствующими положению РЛС и цели в горизонтальной плоскости.

Создаваемые поверхностными волнам локальные уклоны поверхности приводят к тому, что условие зеркального переотражения выполняется для углов скольжения, не только равных , но и в точках O₁ и O₂, лежащих слева и справа от точки O₀, (в которой выполняется условие ). Переотражение от этих точек показано пунктирной линией. Вероятность переотражения в направлении цели при угле , отличном от , определяется вероятностью наличия на морской поверхности уклонов соответствующей величины.

Очевидно, что точка O₂ не может смещаться вправо дальше перпендикуляра, проведенного от цели к морской поверхности. Соответственно минимальный угол скольжения, при котором может происходить переотражение на цель должен быть больше .

В натурных измерениях, как правило, определяются не углы уклонов  поверхностных волн, а уклоны , являющиеся пространственными производными возвышения поверхности [12]. Между собой эти характеристики связаны нелинейным соотношением . Поскольку уклоны поверхностных волн малы, при расчетах обычно предполагается выполнение численного равенства . Это предположение не приводит к значительной ошибке. При расчете дисперсии угла уклонов  погрешность составляет менее 8 % [5]. В первом приближении, пренебрегая нелинейными эффектами в поле морских волн [9], можно принять, что уклоны морской поверхности распределены по нормальному закону.

В случае низкого расположения антенны над морем коэффициент отражения определяется выражением [2]:

                            (3)

 

где  – коэффициент отражения Френеля;  – поляризация;  – дисперсия возвышений поверхности;  – длина радиоволны. Введем обозначение:  – горизонтальная поляризация; – вертикальная поляризация. Коэффициент отражения Френеля является комплексной величиной. При когерентной локации коэффициент Френеля, который зависит от вида поляризации, определяется выражениями [13, 14]:

– для горизонтальной поляризации

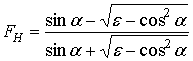,                                    (4)

 

– для вертикальной поляризации

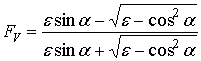,                                  (5)

 

где  – относительная диэлектрическая проницаемость морской воды; . Из выражений (3)-(5) следует, что при зеркальном отражении радиоволн от морской поверхности происходит сдвиг фазы, величина которого зависит от их поляризации.

Относительная диэлектрическая проницаемость морской воды под поверхностью раздела океан-атмосфера не является константой. Она зависит от температуры, солености и частоты падающей на поверхность радиоволны [4,14]. Изменение физико-химических характеристик воды необходимо учитывать, как при анализе квазизеркального отражения, так и при анализе резонансного (брегговского) рассеяния [15].

Рассеянное морской поверхностью электромагнитное излучение может быть представлено в виде суммы среднего (когерентного) поля и флуктуационного (некогерентного) поля с случайными амплитудами и фазами. Даже при малых величинах неровностей морской поверхности рассеяние в направлениях зеркального переотражения перестает быть когерентным. Ошибки, обусловленные некогерентной составляющей, могут быть минимизированы путем накопления сигнала [2] или путем использования сложных широкополосных сигналов [18].

Проанализируем, как меняется фаза отраженного от морской поверхности когерентного радиосигнала. Будем рассматривать ситуацию, когда РЛС и цель находятся на одной высоте. Для численных расчетов примем: ==10 м;  м. Из (2) следует, что =1.1º .

Для выбранных значений высот РЛС и цели и выбранного расстояния между ними, при зондировании в X-диапазоне (длины волн 3.75 – 2.5 см, частоты 8 – 12 ГГц) радиус первой зоны Френеля лежит в пределах от 2.5 м до 3.1 м. В данной геометрии первая зона Френеля остается чистой при амплитуде волны менее 7 м.

 

 

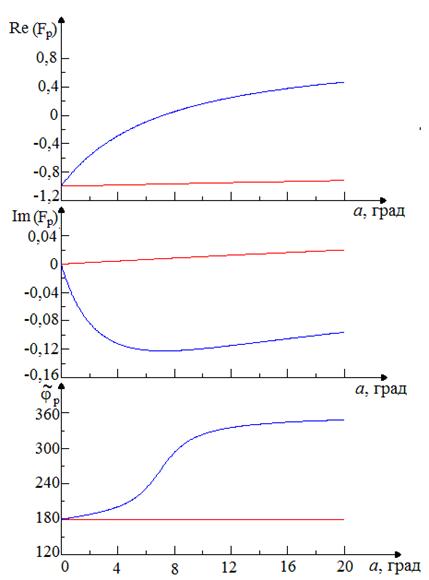
Рис. 2. Зависимости параметров ,  и  от угла скольжения :
красная кривая – горизонтальная поляризация, синяя кривая – вертикальная поляризация

 

Зависимости от угла скольжения действительной  и мнимой  частей коэффициента Френеля, а также фазового сдвига , возникающего при отражении радиоволн от морской поверхности, представлены на рис. 2.

Изменение фазы отраженного радиосигнала определяется отношением действительной и мнимой частей коэффициента Френеля и описывается выражением:

.                                 (6)

При построении рис. 2, на основе результатов работ [2,14] было принято, что относительная диэлектрическая проницаемость морской воды:

.                                                       (7)

Мощность когерентного сигнала, отраженного в направлении цели, определяется квадратом модуля коэффициента Френеля  и диаграммой направленности антенны РЛС. Зависимость этого параметра от угла скольжения представлена на рис. 3.

 

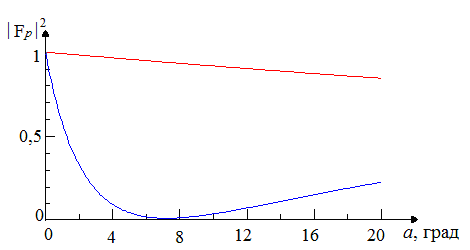
Рис. 3. Зависимость параметра  от угла скольжения

 

Отметим, что при некотором угле скольжения параметр  обращается в ноль. Угол, при котором это происходит, называется углом Брюстера [17].

Из рис. 3 следует, что при малых углах скольжения коэффициент отражения на горизонтальной поляризации должен быть много больше, чем коэффициент отражения на вертикальной поляризации. Это означает, что помехи, создаваемые отражением от морской поверхности, при работе РЛС на разных поляризациях будут различны. Из выражения (3) следует, что отношение мощности радиосигналов на разных поляризациях определяется соотношением

.                                             (8)

Поскольку, как следует из рис. 3, справедливо неравенство , то уровень помех при работе на горизонтальной поляризации выше, чем на вертикальной (см. рис. 4).

 

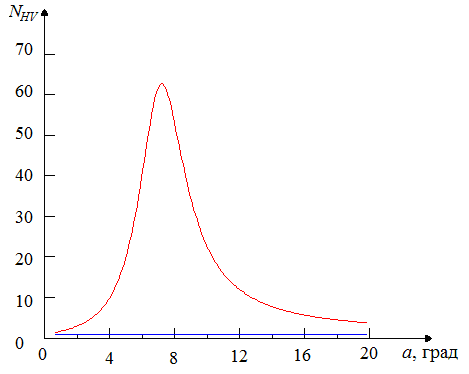
Рис. 4. Зависимость параметра  (красная линия) от угла скольжения .

(синим цветом, показан уровень ).

 

Зависимость уровня помех от скорости ветра

Уровень сигнала, переотраженного морской поверхностью в направлении цели, определяется двумя характеристиками: дисперсией компоненты уклонов  в направлении зондирования и дисперсией возвышений поверхности . Оценим зависимость указанных характеристик от скорости ветра.

Одной из наиболее часто используемых в радиоокеанографии моделей волнового поля является спектральная модель Пирсона-Московитца [18]. Модель описывает развитое волновое поле, характеристики которого определяются единственным параметром – скоростью и направлением ветра. В рамках этой модели дисперсия возвышения поверхности  описывается выражением

.                                            (9)

 

где  – гравитационное ускорение;  – скорость ветра, на высоте 10 м над невозмущенной морской поверхностью. Выражение (9) получено в приближении, которое не учитывает эффекты, связанные с групповой структурой поверхностных волн, а также эффекты, приводящие к потере когерентности морских волн и отклонению распределений возвышений морской поверхности от распределения Гаусса [19,20-25].

Зависимость среднеквадратических величин  возвышений морской поверхности от скорости ветра показана на рис. 5a. Параметр  связан с значимой высотой волн  (значимой высотой волн является средняя высота одной трети самых высоких волн) соотношением .

 

Рис. 5. Характеристики морской поверхности при разных скоростях ветра:

а – зависимость среднеквадратической величины возвышений морской поверхности  от скорости ветра W;

b –зависимости дисперсий уклонов в направлении  (красная линия) и поперек  (синяя линия) направления ветра.

 

Для моделирования зависимости уклонов морской поверхности от скорости ветра воспользуемся результатами прямых натурных измерений уклонов, выполненных с помощью двумерного лазерного уклономера [26]. Согласно результатам этой работы зависимость дисперсий компонент уклонов в продольном (вдоль направления ветра) и в поперечном направлении можно аппроксимировать выражениями:

0,00410+0,00205,                                 (10)

0,00136+0,00162.                                 (11)

Регрессионное уравнение (10) справедливо со среднеквадратическим отклонением ±0,005, регрессионное уравнение (11) справедливо со среднеквадратическим отклонением ±0,004. Зависимости дисперсий уклонов в рассчитанные для двух направлений, вдоль  и поперек  ветра представлены на рис. 5b.

Даже при скорости ветра, равной нулю, параметры  и , согласно построенным на основе данных измерений регрессионным уравнениям отличны от нуля [12,26]. Объясняется это тем, что морская поверхность никогда не остается спокойной. Волны зыби могут распространяться на сотни километров, и условия в районе, где работает РЛС, определяет не только локальный ветер, но и метеорологическая обстановка в удаленных районах. Детальные натурные исследования при штиле и слабых ветрах показали, что, когда вся поверхность является сликом (областью, где подавлены или не генерируются короткие поверхностные волны), дисперсия уклонов отлична от нуля и не зависит от скорости ветра.

Функции плотности вероятностей уклонов морской поверхности, рассчитанные при характерных значениях статистических моментов уклонов при разных скоростях ветра, приведены на рис. 6. Распределения уклонов построены вдоль и поперек направления ветра. Из рис. 6 следует, что с усилением ветра область на морской поверхности, от которой может происходить зеркальное отражение, расширяется. Одновременно снижается вероятность отражения под углом .

 

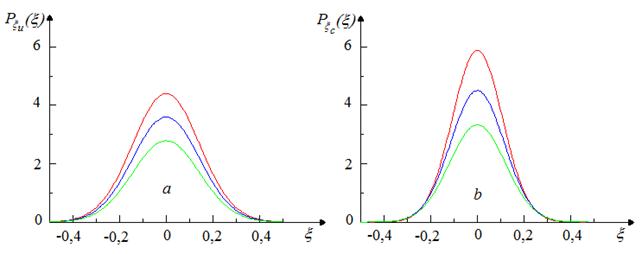
Рис. 6. Плотность вероятностей уклонов морской поверхности: а – уклоны вдоль направления ветра, b – уклоны поперек направления ветра. (Красная линия – 2 м/с; синяя линия – 4 м/с; зеленая линия – 8 м/с).

 

Уровень сигнала, отраженного от морской поверхности, определяется не только характеристиками поверхности, но и шириной диаграммы направленности антенны. Для излучающей антенны зададим диаграмму направленности в форме функции Гаусса

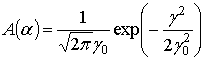 ,                                (12)

 

где  – параметр, определяющий ширину диаграммы направленности. Нетрудно показать, что в случае, когда функция  описывается выражением (12), параметр  связан с полушириной диаграммы направленности антенны РЛС, определяемой по уровню половинной мощности, соотношением .

При расчете мощности сигнала, отраженного морской поверхностью в направлении цели, необходимо учитывать, что вероятность зеркального отражения определяется вероятностью, соответствующей ориентации уклонов поверхности. Мощность сигнала, отраженного морской поверхностью в направлении цели, описывается интегральным выражением:

.                          (13)

Отметим, что поле уклонов морской поверхности является анизотропным. Дисперсия компонент уклонов, ориентированных в направлении ветра, выше, чем дисперсии уклонов в поперечном направлении. Соответственно будут различаться мощности сигналов, отраженных морской поверхностью, при ориентации РЛС.

Динамика изменения уровня помехи с изменением скорости ветра показана на рис. 7. За нулевой уровень принят уровень мощности отраженного от морской поверхности сигнала при работе РЛС на горизонтальной поляризации. Расчеты проведены для длины радиоволны 3 см.

 

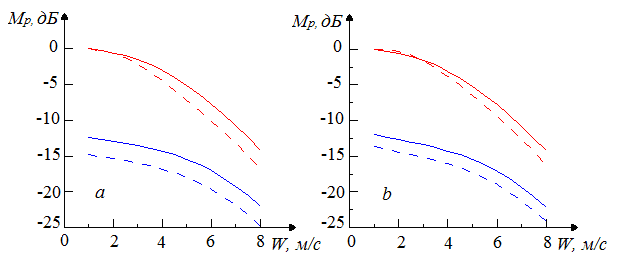
Рис. 7. Зависимость параметра  от скорости ветра :

а – распространение радиоволн вдоль направления ветра, b – поперек;

красные линии соответствуют горизонтальной поляризации, синие линии – вертикальной; сплошные линии – =2º, штриховые – =5º.

 

Из рис. 7 следует, что с увеличением скорости ветра, уровень помех, как на вертикальной, так и на горизонтальной поляризациях, снижается. При изменении скорости ветра от 1 м/с до 8 м/с изменение уровня помехи превышает 10 дБ. Помехи, создаваемые зеркальным отражением от морской поверхности на горизонтальной поляризации, по интенсивности на порядок превышают помехи на вертикальной поляризации.

Следует отметить, что проведенный выше анализ соответствует слабым или умеренным скоростям ветра, т.е. условиям, когда обрушения поверхностных волн не происходят или их интенсивность достаточно мала, чтобы этим эффектом пренебречь. При высоких скоростях ветра необходимо учитывать отражения от пенных образований, возникающих при обрушении волн, от брызг, а также от заостренных гребней волн, возникающих перед обрушением, на которых не выполняется условие (1) [10,27]. С ростом скорости ветра возрастает роль диффузного отражения [11].

Выводы

Проведен анализ уровня помех, обусловленных взволнованной морской поверхностью, в зависимости от скорости ветра при работе РЛС по низколетящим целям. Приведены основные расчетные соотношения для расчета интенсивности пассивной помехи при различных условиях. Анализ выполнен для радиоволн сантиметрового диапазона. При этом использованы данные натурных измерений. Показано, что с увеличением скорости ветра, уровень помех, вызванных зеркальным отражением от морской поверхности, снижается как на вертикальной, так и на горизонтальной поляризациях. При изменении скорости ветра от 1 м/с до 8 м/с изменение уровня помехи превышает 10 дБ. Помехи, создаваемые зеркальным отражением от морской поверхности на горизонтальной поляризации, по интенсивности на порядок превышают помехи на вертикальной поляризации.

Приведенные результаты имеют важное практическое значение при создании моделей пассивных помех, используемых при разработке алгоритмов обработки сигналов, отраженных целями на фоне морской поверхности. 

 

Литература

1. Штагер Е.А. Отражение радиоволн от кораблей и других морских объектов // СПб. Издательство ВВМ при СПб Государственном университете. 2005. 418 c.

2. Нгуен Тхань Хынг Повышение угловой точности фазово-фазовых моноимпульсных РЛС при сопровождении низколетящих над морем целей на проходе // Изв. СПбГЭТУ “ЛЭТИ”. Сер. Радиоэлектроника и телекоммуникации. 2004. № 2. С. 46-52.

3. Запевалов А.С. Изменчивость характеристик локальных уклонов морской поверхности // Прикладная гидромеханика. 2005. т. 7. № 1. С. 17.

4. Исимару А. Распространение и рассеяние волн в случайно-неоднородных средах. М.: Мир, 1981. Т. 2. 322 с.

5. Запевалов А.С., Лебедев Н.Е. Моделирование статистических характеристик поверхности океана при дистанционном зондировании в оптическом диапазоне // Оптика атмосферы и океана. 2014. т. 27, № 1. С. 28-33.

6. Показеев К.В., Запевалов А.С., Пустовойтенко В.В. Моделирование формы отраженного импульса радиоальтиметра // Вестник Московского университета, Физика. Астрономия. 2013. № 5. С. 80-85.

7. Arnold-Bos A., Khenchaf A., Martin A. Bistatic radar imaging of the marine environment – Part I: Theoretical background // IEEE Trans. Geosci. Remote Sens. 2007. v. 45. P. 3372–3383.

8. Zhang M., Nie D., Yin H-C A versatile composite surface model for electromagnetic backscattering from seas // Waves in Random and Complex Media. 2011. v. 21, No. 2, P. 348–361.

9. Zapevalov A.S., Pustovoitenko V.V. Modeling of the probability distribution function of sea surface slopes in problems of radio wave scattering // Radiophysics and Quantum Electronics. 2010. v. 53, № 2, P. 100-110. DOI: 10.1007/s11141-010-9206-z.

10. Булатов М.Г., Раев М.Д., Скворцов Е.И. Доплеровские спектры сигналов, рассеянных морской поверхностью при настильных углах зондирования (результаты натурного эксперимента) // Современные проблемы дистанционного зондирования Земли из космоса. 2007. Вып.4. Т.1. С. 280-288.

11. Калмыков А.И., Курекин А.С., Островский И.Е., Пустовойтенко В.В. Двухпозиционное рассеяние радиоволн поверхностью моря при малых углах скольжения // Изв. Высших учебных заведений, Радиофизика. 1973. т. 16, № 2. С. 199-205.

12. Bréon F.M., Henriot N. Spaceborne observations of ocean glint reflectance and modeling of wave slope distributions // J. Geoph. Res.: Oceans. 2006. V. 111. № C6.  DOI: 10.1029/2005JC003343.

13. Meissner T., Wentz F.J. The complex dielectric constant of pure and sea water from microwave satellite observations // IEEE Transactions on Geoscience and Remote Sensing, 2004, vol. 42, No. 9, P. 1836-1849.

14. Садовский И.Н., Кузьмин А.В., Шарков Е.А., Сазонов Д.С., Пашинов Е.В., Ашеко А.А., Батулин С.А. Анализ моделей диэлектрической проницаемости водной среды, используемых в задачах дистанционного зондирования акваторий // Препринт. М.: ИКИ РАН, 2002, Пр-2172, 60 с.

15. Запевалов А.С., Пустовойтенко В.В. Влияние физико-химических характеристик морской воды на резонансное рассеяние радиоволн морской поверхностью // Журнал Радиоэлектроника. 2014. № 9. http://jre.cplire.ru/jre/sep14/4/text.pdf.

16. Лукин К.А., Коновалов В.М. Когерентная компенсация мощных мешающих отражений в локаторах с периодическими сигналами // Прикладная радиоэлектроника, 2012, т. 11, № 1, С. 3-14.

17. Долуханов М. П. Распространение радиоволн.  М.: Связь, 1965. 399 с.

18. Serafino F., Lugni C., Borge J.C.N., Zamparelli V., Soldovieri F. Bathymetry determination via X-band radar data: A new strategy and numerical results // Sensors. 2010. v.10. P. 6522-6534.

19. Запевалов А.С., Большаков А.Н., Смолов В.Е. Исследования уровня когерентности морских поверхностных волн // Изв. РАН. Физика атмосферы и океана. 2004. т. 40, № 4. С. 545-549.

20. Запевалов А.С., Большаков А.Н., Смолов В.Е. Моделирование плотности вероятностей возвышений морской поверхности с помощью рядов Грама-Шарлье // Океанология. 2011. т. 51. № 3. С. 432-439.

21. Залевский Г.С., Музыченко А.В., Сухаревский О.И. Метод радиолокационного обнаружения и идентификации металлических и диэлектрических объектов резонансных размеров, расположенных в диэлектрической среде // Известия ВУЗов: Радиоэлектроника. 2012. Т. 55. № 9. С. 11-25.

22. Рудаков И.С., Рудаков С.В., Богомолов А.В. Методика идентификации вида закона распределения параметров при проведения контроля состояния сложных систем // Информационно-измерительные и управляющие системы. 2007. Т. 5. № 1. С. 66-72.

23. Залевский Г.С., Сухаревский О.И. Расчет характеристик рассеяния воздушных радиолокационных объектов резонансных размеров, основанный на итерационном алгоритме // Известия высших ВУЗов: Радиоэлектроника. 2014. Т. 57. № 6 (624). С. 13-25.

24. Коломиец Л.В., Федоров М.В., Богомолов А.В., Мережко А.Н., Солдатов А.С., Есев А.А. Метод поддержки принятия решений по управлению ресурсами при испытаниях авиационной техники // Информационно-измерительные и управляющие системы. 2010. Т. 8. № 5. С. 38-40.

25. Залевский Г.С., Сухаревский О.И., Василец В.А., Нечитайло С.В. Вторичное излучение резонансных идеально проводящих объектов // Радиотехника и электроника. 2014. Т. 59. № 12. С. 1159.

26. Христофоров Г.Н., Запевалов А.С., Бабий М.В. Измерения параметров шероховатости морской поверхности при переходе от штиля к ветровому волнению // Изв. АН СССР. Физика атмосферы и океана. 1992. т. 28, № 4. С. 424-431.

27. Sharkov E.A. Breaking ocean waves: geometry, structure and remote sensing // Berlin, Heldelberg, New York : Springer / PRAXIS, 2007. 278 p.