УДК 621. 396. 677

МОНОИМПУЛЬСНАЯ ПЕЛЕНГАЦИЯ ЦЕЛИ ОТНОСИТЕЛЬНО БОРТОВОЙ РЛС В ИНВЕРСНОЙ БИСТАТИЧЕСКОЙ СИСТЕМЕ

 

E. А. Лайко, Д. Г. Калько, С. А. Торбин

Военная академия войсковой ПВО Вооруженных Сил РФ имени маршала Советского Союза А. М. Василевского (г. Смоленск)

Статья получена 3 марта 2015 г.

 

Аннотация.  Рассмотрен способ моноимпульсной обработки на земле отраженных от цели сигналов, излучаемых бортовой станцией подсвета для определения пеленга воздушной цели относительно антенны бортовой станции. Обоснована возможность фазовой суммарно-разностной пеленгации воздушного объекта на земле относительно бортовой станции, антенна которой излучает сигналы подсвета на разных частотах секторами с разными фазовыми центрами.

Ключевые слова: сканирование, цель, моноимпульсный пеленгатор.

Abstract: The way of monopulse processing on the ground, reflected from the target signals, radiated by the illumination airborne radar, to determine the target bearing concerning the airborne antenna is considered. The possibility of use phase sum-difference air-to-air direction finding on the ground concerning the airborne antenna which radiates illumination signals at different frequencies by the sectors with different phase centers is proved.

Key words: scanning, target, monopulse radar.

 

Введение

Одной из существенных проблем радиолокационной скрытности наземных станций наведения в полуактивных и комбинированных системах управления является необходимость длительного радиоизлучения в сторону пеленгуемого воздушного объекта. Традиционная полуактивная система самонаведения включает наземную станцию подсвета, излучающую в направлении воздушного объекта (ВО), и объект управления (ОУ) с пассивным радиопеленгатором, принимающим отраженные от ВО сигналы [1]. Отраженные от ВО сигналы, принятые радиопеленгатором, обрабатываются известными моноимпульсными методами радиопеленгации [2].

Скрытность наземных средств управления можно повысить, если применить обратную или инверсную полуактивную систему самонаведения, суть которой заключается в том, что  ОУ излучает в направлении пеленгуемого объекта сам (рис. 1), а сигналы, отраженные от ВО, принимаются на земле станцией управления (СУ). При этом СУ на земле по отраженным от ВО сигналам должна определять углы рассогласования ВО относительно оптической оси антенны ОУ.

Возникает задача, измерения на земле углов рассогласования между направлением на пеленгуемый ВО и направлением оптической оси антенны ОУ по сигналам, излучаемым антенной ОУ.

Цель работы – обосновать способ излучения радиосигналов антенной ОУ в направлении  ВО и способ их обработки в наземной радиолокационной станции (РЛС) для измерения пеленга ВО  относительно ОУ.

 

Инверсная полуактивная система самонаведения с частотным разделением каналов

Рассмотрим подробнее инверсную полуактивную бистатическую систему с частотным разделением каналов. Допустим ОУ имеет антенну, состоящую из четырех секторов 1, 2, 3 и 4 с комплексными характеристиками направленности на передачу  и , где  и – рассогласования направления на ВО относительно равносигнального направления антенны ОУ в вертикальной и горизонтальной плоскостях. К каждому из этих секторов подключены передатчики (ПРД), которые формируют радиосигналы на несущих частотах f₁, , , . Разности частот излучения будет равны ,  и .

Сигналы на частотах f₁, f₂, f₃ и f₄ излучаются секторами антенны в направлении  ВО, отражаются им и достигают антенны наземной СУ. Коэффициент направленного действия антенны СУ в направлении ВО для каждой из частот равен и .

Для когерентности обработки должна быть предусмотрена передача опорных сигналов с ОУ на наземную РЛС (рис. 1). Поэтому ОУ имеет опорную антенну, которая излучает опорные сигналы на четырех частотах. Причем перед излучением опорных сигналов необходимо их перенести в другой диапазон частот для развязки в головном канале наземной СУ с сигналами, отраженными от ВО. В частности такую операцию можно выполнить на цифровых делителях частоты, поскольку современные делители функционируют на частотах свыше 8 ГГц. Частоты опорных сигналов делятся в N раз, затем смешиваются в сумматоре и поступают на общую передающую антенну опорного канала ОУ. Если воспользоваться специализированными микросхемами деления частоты таких как ADS 5001, можно сформировать сигналы на частотах  f₁,  f₂, f₃ и f₄ путем добавления частоты  к опорной частоте f_1,  причем частоту  можно получать путем деления самой опорной частоты f₁ на N. Тогда вместо четырех опорных сигналов можно обойтись одним, из которого в дальнейшем можно сформировать остальные опорные сигналы для гетеродинирования частот f₁, f₂, f₃ и f₄ на земле. Опорный приемник СУ принимает опорные сигналы, усиливает их и передает в преобразователь частоты,  на который поступает также сигнал с местного гетеродина на частоте . После преобразования спектр опорных сигналов на частотах , , и  переносится на промежуточные частоты, равные , ,  и . Перенос опорных частот на промежуточную, выполняется для их развязки, так как разница между ними может составлять от единиц до десятков мегагерц.  При такой разнице частот отделить их друг от друга на сверхвысокой частоте сложно из-за трудностей изготовления узкополосных полосовых фильтров.

Опорные сигналы на промежуточных частотах выделяются полосовыми фильтрами опоры (рис. 1), настроенными каждый на свою промежуточную частоту. После разделения опорных частот они тем же сигналом местного гетеродина переносятся по частоте вверх. Тем самым устраняется сдвиг фазы, вносимый местным гетеродином. После преобразователей частоты вверх каждый выделенный опорный сигнал поступает на умножитель частоты, коэффициент умножения которого равен N. Таким образом, на преобразователи частоты головного приемника СУ будут раздельно поступать четыре опорных сигнала, причем каждый – в свой преобразователь.

 

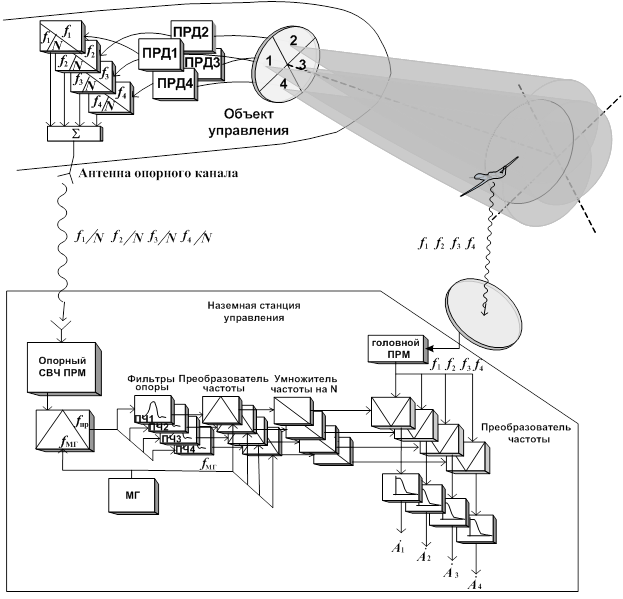
Рис. 1 Структурная схема инверсной полуактивной системы

 

После преобразования и фильтрации сигналов низкой частоты можно получить комплексные огибающие сигналов, изменяющиеся с частотами Доплера ,, и, которые определяются изменением расстояний прохождения головных и опорных сигналов. Для того чтобы уяснить свойства такой системы, рассмотрим математические модели сигналов головного и опорного приемников.

 

Математические модели сигналов

Математическая модель сигнала, излучаемого i-м сектором антенны ОУ на частоте , и принимаемого антенной головного канала  СУ может быть представлена в виде

,

 

где – комплексная амплитуда отраженного сигнала ВО, излученного i-м  сектором антенны ОУ в направлении ВО и принятого головной антенной СУ;

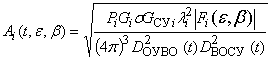 – модуль комплексной амплитуды отраженного сигнала ВО;

 – средняя мощность непрерывного излучения передатчика i-го сектора антенны  ОУ;

– коэффициент направленного действия i-го сектора антенны ОУ;

 – комплексная характеристика нормированная по амплитуде направленности i-го сектора антенны ОУ;

 – эффективная площадь рассеяния ВО в направлении наземной РЛС;

– длина волны излучения i-го сектора антенны  ОУ;

с – скорость света;

– текущая дальность между ОУ и ВО;

– текущая дальность между ВО и СУ.

Модели характеристик направленности секторов антенны запишем в виде системы

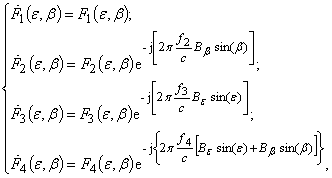
где

 –

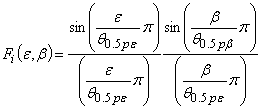упрощенная модель амплитудной характеристики направленности сектора антенны (для упрощения модели амплитудные характеристики остальных секторов антенны для фазовой системы формально можно принять равными друг другу);

– базы (расстояния) между фазовыми центрами секторов антенны ОУ.

Текущие дальности  и  представим в виде

 

;                                            (1)

 

,                                             (2)

 

где , – начальные дальности между  ОУ и ВО, а также между СУ и ВО;

,  – радиальные скорости сближения по направлениям ОУ–ВО и СУ–ВО.

Для сигнала опорного канала, принимаемого опорной антенной, не предъявляются строгие требования в плане неизмеримости амплитуды. Поскольку опорный сигнал обладает достаточной мощностью, то его модель можно представить в виде

,

 

где  – текущая дальность  ОУ–СУ, определяемая как

 

,                                          (3)

 

 – начальная дальность ОУ–СУ, и радиальная скорость удаления по направлению  ОУ–СУ.

Для обоснования способа моноимпульсной пеленгации на земле примем равными нулю фазовые погрешности приемника  опорного канала СУ на разных частотах и передающих каналов секторов ОУ. Тогда различные паразитные фазовые сдвиги и задержки опорных сигналов можно принять равными нулю. После преобразования частот в смесителях головного канала и низкочастотной фильтрации сигналы с выхода каждого из четырех фильтров низкой частоты можно представить в виде

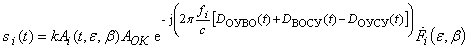,             (4)
 

где k – коэффициент преобразования частоты в смесителях головного канала.

Представив фазу комплексной характеристики направленности i-го сектора антенны как , а также подставив в (4) дальности (1), (2) и (3) перепишем (4) в виде

 

или, раскрыв скобки в показателе степени экспоненты, в виде

,   (5)

где величина  – частота Доплера i-го сигнала на частоте излучения , а величина  – начальная фаза сигнала на частоте .

Учитывая частоту Доплера и начальную фазу сигнала, обусловленную разностью дальности ОУ–СУ и суммы дальностей ОУ–ВО и ВО–СУ, перепишем (5) в виде

.                    (6)

Анализ (6) показывает, что кроме фазы, обусловленной частотой Доплера и фазы, обусловленной разностью хода лучей  от разных секторов антенны ОУ, i-й сигнал имеет также фазовый сдвиг , обусловленный разностью дальностей. Если бы частоты всех секторов антенны были бы равны, то этот фазовый сдвиг для всех секторов был бы одинаков. Однако при разности частот  разность начальных фаз, обусловленных дальностями, будет равна

                        (7)
 

и при определенных условиях может иметь существенное значение.

Преобразуем сигнал (6) в дискретную форму вида

,

где – интервал дискретизации сигнала по времени.

При обработке временной выборки сигнала длительностью  с помощью дискретного преобразования Фурье (ДПФ) сигнал (7) умножается на комплексно-сопряженные отсчеты k-й экспоненты вида , где . За время выборки ВО не успеет приблизиться настолько, это привело к изменению амплитуды сигнала . Поэтому примем ее постоянной за время выборки, т. е. . Тогда ДПФ сигнала (7) будет иметь вид

,                (8)
 

в котором вынесем экспоненты с начальными фазами за знак суммы и преобразуем (8) к виду

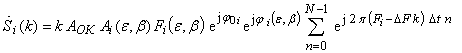.    (9)
 

Сумма в выражении (9) представляет собой сумму членов геометрической прогрессии, где – это знаменатель прогрессии. Поэтому

.

 

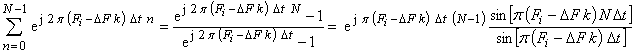Тогда k-й отсчет ДПФ будет иметь вид

.

 

Для фильтра ДПФ, частота которого совпадает с частотой Доплера  i-го сектора антенны (звенящий фильтр) комплексное число  будет иметь значение

,

которое зависит только от амплитуд и фаз характеристик направленности сектора антенны ОУ, а также от сдвига фаз, возникающего за счет разности частот излучения, где . С учетом разности фаз (7) амплитуды разностных и суммарного сигналов можно определить как

;  (10)

; (11)

.   (12)

 

Фазовая фокусировка сигналов

Анализ (10)–(12) показывает, что в составе сигналов разностных и суммарного каналов присутствуют комплексные амплитуды с паразитной разностью фаз из-за разности частот излучения. Поэтому прежде чем оценивать пеленги, необходимо в сигналы второго, третьего и четвертого секторов антенны внести поправки на разность фаз , 2 и 3, обусловленные  геометрией относительного расположения ОУ, ВО и СУ на момент начала накопления выборки, когда дальности равны , и .

Для оценки значений начальной фазы необходимо учесть значения дальностей на текущий момент времени t. Например, суммарная дальностная ошибка ΔD=5м обусловливает равную 6ошибку оценки разности фаз, поэтому при оценивании пеленгов необходимо периодически различными методами поиска подбирать адекватные значения разности фаз, изменение которых следует экстраполировать на следующий такт оценивания. После экстраполяции с комплексными амплитудами звенящих фильтров необходимо проводить ДПФ.

При одной и той же разности частот излучения между частотами f₁, f₂, f₃ и f₄ разность фаз  между сигналами смежных частот одинакова. Ее величина находится в пределах от нуля до 360 градусов. Эту разность фаз можно искать по максимуму суммарного сигнала. Введем векторы амплитуд суммарного и разностных каналов в k-м дискрете Доплера вида

,

,

.

 

и фокусирующий вектор

.

 

Построим результирующую амплитуду суммарного канала в виде

.                                                          (13)

Изменяя угол фазирования φ от 0 до 360º, найдем значение фазы φ, при которой  имеет максимум (рис. 2).

 

 

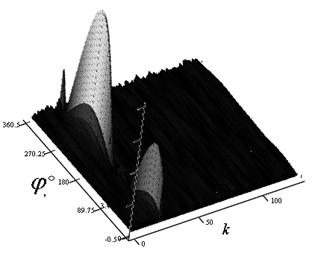
Рис. 2 Дискретные преобразования Фурье для различных фокусирующих множителей с фазой φ

 

Определив значение фазы, при которой суммарная амплитуда (13) имеет максимум, проведем фазирование разностных каналов на основе выражений

;

.

Найдя сфокусированные комплексные амплитуды суммарного и разностных каналов для величины φ, при которой амплитуда суммарного канала достигает максимума, можно определить пеленги ВО по углу места и азимуту относительно равносигнального направления антенны ОУ (рис. 3).

 

 

Рис. 3 Определение пеленга воздушной цели после фазовой фокусировки сигналов

 

Заключение

При применении инверсной бистатической системы с фазовыми методами пеленгации одним из важных теоретических вопросов является фазовая фокусировка доплеровских портретов, которая необходима в связи с разностью частот излучения секторами антенны. В настоящей статье показан вариант фазовой фокусировки доплеровских спектров методом максимума суммарного сигнала. Предложенный метод может найти применение в перспективных скрытных полуактивных радиолокационных системах, построенных на принципах инверсной бистатической радиолокации. Можно для фокусировки использовать также и методы минимума среднеквадратической ошибки, а также  другие методы, приводящие так или иначе к одному и тому же результату.

Для реализации инверсной бистатической системы можно использовать и временное разделение каналов. Однако здесь также потребуется фазовая фокусировка доплеровских портретов, компенсирующая сдвиги фаз за счет движения цели. Таким образом анализ моделей сигналов показывает возможность применения фазовых методов пеленгации в инверсных бистатических радиолокационных системах при условии фазовой фокусировки сигналов.

 

Литература

1. Демидов В. П., Кутыев Н. Ш. Управление зенитными ракетами. –2-е изд., М.: Воениздат, 1989. – 335 с.

2. Леонов А. И., Фомичев К. И. Моноимпульсная радиолокация. –2-е изд. М.: Радио и связь, 1984. – 312 с.