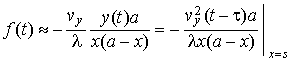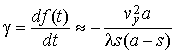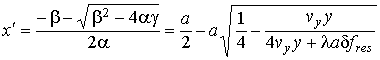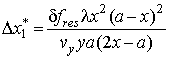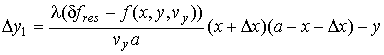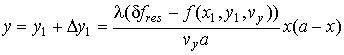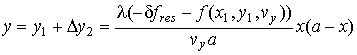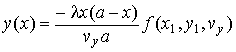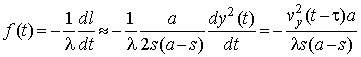УДК 621.396.96

Разрешающая способность просветного радиолокатора

 

А. Н. Ковалев, Ф. Н. Ковалев, В. В. Кондратьев

Нижегородский государственный технический университет им. Р.Е. Алексеева

 

Статья получена 28 февраля 2015 г.

 

Аннотация. Рассматривается проблема разрешения объектов в просветной радиолокационной системе с монохроматическим излучением и измерениями доплеровской частоты рассеянного сигнала. Получены выражения для расчета границ области разрешения объектов. Показано, что для повышения разрешающей способности следует использовать направленные свойства антенн или прием сигнала в разнесенных пунктах.

Ключевые слова: бистатическая радиолокационная система, просветная радиолокация, разрешающая способность, доплеровская частота, разрешение сигналов по частоте.

Abstract. The problem of resolution of targets in forward-scattering radar system with monochromatic radiation and measuring the Doppler frequency is considered. Formulas for calculating the boundaries of the region of resolution are obtained. Attention is paid to the possibility of increasing the resolution of targets due to the use of directional antennas or several spaced apart receivers.

Keywords: bistatic radar system, forward-scattering radar, resolution of targets, Doppler frequency, frequency resolution.

 

Введение

Просветная радиолокация является уникальным средством обнаружения маловысотных и малоразмерных целей, в том числе объектов, выполненных по технологии Stealth [1,2,3]. Просветные радиолокационные системы (РЛС) имеют ряд особенностей: большое разнесение передающей и приемной антенн, узкую и протяженную вдоль линии базы зону действия [2], специальные методы определения координат по измерениям доплеровской частоты рассеянного сигнала [4-12].

В настоящей работе рассмотрена еще одна важная характеристика просветных РЛС – разрешающая способность (способность раздельного радиолокационного наблюдения близко расположенных объектов). Представленные исследования проведены для простейшей радиолокационной системы с монохроматическим передатчиком и приемником с амплитудным детектированием суммарного колебания, образуемого в результате интерференции прямой радиоволны, излученной передатчиком, и радиоволны, рассеянной на объекте [3,6,12,13,14]. Измеряемым параметром в приемнике является доплеровская частота. Исследования развивают результаты работы [15] и проведены в рамках приближенного представления доплеровской частоты в виде линейной функции времени для объектов, движущихся ортогонально линии базы [8,10,11].

На рис. 1 показана схема просветной двухкоординатной РЛС. Элементы системы размещены в плоскости xOy: приемник (Receiver) R – в начале системы координат (в точке О), передатчик (Transmitter) T – на оси Ox на расстоянии a от приемника, называемом базой. Объект движется со скоростью  в плоскости xOy, пересекая в момент времени τ линию базы под углом ψ в точке с координатами , .  – расстояние от передатчика до объекта,  – расстояние от объекта до приемника.

 

Рис. 1. Схема просветной бистатической РЛС на плоскости

 

В просветной РЛС наблюдение объекта осуществляется на небольших удалениях от линии базы [2,8,10,11,14,15]:  

,   .                                           (1)

 

Как следствие, в качестве модели движения объекта обычно рассматривают равномерное прямолинейное движение c углами ψ близкими к 90° [2,8,10,11,14], так что текущие координаты объекта можно представить в виде:

,                                                    (2)

,                                                         (3)

,                                                              (4)

 

где t – время, , ,  – величина скорости.

Доплеровская частота рассеянного сигнала [16,17]

                                                    (5)

 

с учетом модели движения (2) ÷ (4) и узости зоны действия может быть выражена приближенно [8,10]:

,                  (6)

 

λ – длина волны излучения передатчика,  – суммарная дальность объекта до передатчика и до приемника.

Из (6) видно, что на небольших удалениях объекта от линии базы доплеровская частота является квазилинейной функцией времени со скоростью изменения [15]:

.                                         (7)

 

Выражения (6), (7) удобно использовать для анализа разрешающей способности рассматриваемой РЛС.

В работе на основе (6), (7) проводится исследование разрешающей способности системы по координатам x, y. Полагается, что в зоне действия системы находятся два движущихся с одинаковой скоростью объекта, сигналы от которых можно разрешить при сдвиге их частот на величину [15,17]:

 

,                                                         (8)

 

где  – интервал накопления-анализа сигнала, в течение которого производится измерение доплеровской частоты. Обычно  много меньше полного времени наблюдения  объекта, пересекающего зону действия (на интервале  доплеровская частота измеряется многократно [8,12,14,18]).

1. Разрешение по координате y

Исследование разрешающей способности удобно провести сначала для каждой из координат x, y по отдельности, полагая другую координату объектов одинаковой. А затем полученные результаты обобщить на случай смещения объектов и по x и по y.

Пусть рассеянные на объектах сигналы фиксируются раздельно, если объекты находятся на расстоянии Δy друг от друга. Тогда разрешающую способность системы по координате y можно найти из условия разрешения сигналов по частоте:

 

,                                                  (9)

 

где  и  – доплеровские частоты сигналов от первого и второго объектов, имеющих одинаковую скорость  и координаты  и  соответственно:

 

.                      (10)

Если

,                                                    (11)

 

то следует положить, что объекты не разрешаются. Нахождение границ (9) области разрешения сводится к решению двух уравнений

 

,                        (12)

 

которые при использовании (6) принимают вид

 

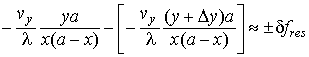
и дают решения [15]

,                                             (13)

,                                           (14)

 

где  определяется временем анализа  (8).

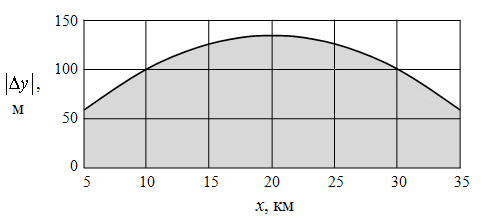
Из (13), (14) видно, что . На рис. 2 представлен график зависимости , , от координаты x (одинаковой у объектов), вычисленный при следующих параметрах системы: , , ; , . Область значений , при которых объекты не разрешаются, выделена серым цветом.

 

 

Рис. 2. Зависимость разрешающей способности системы

по координате y от координаты x

 

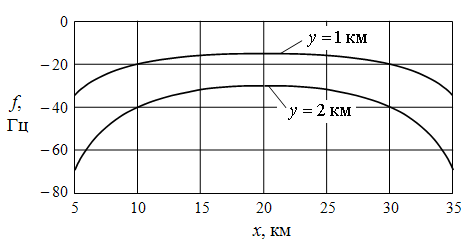
Также из (13), (14) следует независимость  от знака  и симметрия  относительно центра базы ( – см. рис. 2), что в свою очередь является проявлением симметрии доплеровской частоты (5), (6) [13,14]. График зависимости (6) доплеровской частоты от координаты x показан на рис. 3.

 

Рис. 3. Зависимость (6) доплеровской частоты от координаты x объекта (, , , )

 

Важным свойством разрешающей способности по координате y является независимость от самой координаты y [15]. Как будет показано далее, это не выполняется для разрешающей способности по координате x.

Частный случай (13), (14) можно получить для системы с интервалом  [18,19], где  определено из (7):

,                             (15)

 

 – радиус первой зоны Френеля [3]. Величину  можно трактовать как предельное разрешение системы по параметру y при построении первичной обработки без учета частотной модуляции сигнала на интервале .

При выборе   меньшем величины :

 

,  ,

 

из (13), (14) несложно получить:

 

,

 

то есть  увеличивается в  раз (разрешение ухудшается).

2. Разрешение по координате x

Разрешающую способность системы по координате x можно найти также из уравнения (9), полагая объекты сдвинутыми только по координате x:

 

.                                (16)

или

.

 

Уравнение (16) после подстановки в него выражения для доплеровской частоты (6) преобразуется к двум квадратным:

 

,                                                    (17)

,                                                    (18)

 

, ,

 

,     ,

 

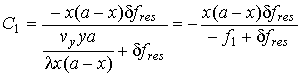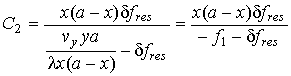с решениями

 

,   ,              (19)

 

для уравнения (17) и

 

,   ,             (20)

 

для уравнения (18). Величина  в (17) ÷ (20) определяется временем анализа  (8).

На рис. 4 в качестве примера приведены графики зависимостей , , , (19), (20) от координаты x первого объекта, вычисленные при тех же условиях, что и график на рис. 2. Для рис. 4 значение координаты y (одинаковой для объектов) взято равным 1 км. На рис. 5 показан аналогичный график, но вычисленный уже для . Область значений , при которых объекты не разрешаются, выделена серым цветом.

 

 

Рис. 4.  Зависимость разрешающей способности системы

по координате x от координаты x первого объекта ()

 

 

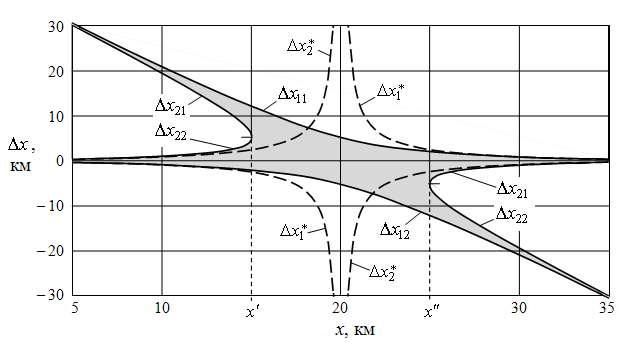
Рис. 5.  Зависимость разрешающей способности системы

по координате x от координаты x первого объекта ()

 

Из рис. 4, 5 видно, что уравнение (16) имеет два решения (при ), или четыре решения, что отражает симметрию зависимости доплеровской частоты относительно абсциссы  (рис. 3).

Если уравнение (16) имеет четыре решения, то два из них (,  или , ) расположены в окрестности первого объекта – точки с координатами (x, y), а два других (,  или , ) – в окрестности точки с координатами . Если два решения – то оба расположены в окрестности первого объекта.

Значения  и , при которых происходит слияние зон, соответствующих интервалу  и расположенных симметрично по обе стороны от центра базы , определяются из условия равенства нулю дискриминанта уравнения (18) при  или уравнения  (17) при , т.е.

 

.                                                            (21)

или  соответственно

.

 

Так, для рассматриваемых на рис. 4, 5 примеров скорость  положительна (), и ,  находятся как решения квадратного уравнения (21):

 

 

,         (22)

,

 

где ,  ,  . При этом для  и  выполняются равенства:

 

,  ,

 ,  .

 

Из (22) следует, что при уменьшении  (увеличении времени анализа ) интервал (, ) уменьшается, и разрешающая способность системы по координате x повышается.

Сравнение графиков на рис. 4, 5 и рис. 2 показывает, что разрешающая способность системы по координате x значительно хуже, чем по y. Например,  для координат первого объекта  и  из (19), (20) следует м, м, в то время как согласно (13), (14) м. Аналогичный эффект наблюдается при сравнении точности определения координат x и y в просветных бистатических РЛС [20] или РЛС с разнесенными приемниками [6,9,13].

Причиной слабого разрешения по координате x является слабая  чувствительность доплеровской частоты к отклонению координаты x на большей части базы РЛС (рис. 3).

Другой отличительной особенностью разрешающей способности по x является ее зависимость от координаты y объекта, что видно из сравнения графиков на рис. 4 и 5: с уменьшением  разрешение по x ухудшается и при  оно отсутствует.

Для малых , , , и областей, удаленных от центра базы, , из (6), (16) можно получить приближение:

 

,

 

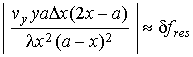и еще один вариант формул для оценки разрешающей способности по x: 

 

,                                            (23)

.                                           (24)

 

 

Результаты расчетов по (23), (24) для рассматриваемых примеров также изображены на рис. 4, 5 (штриховые линии). Из приведенных графиков видно, что приближения (23), (24) дают удовлетворительные результаты только на краях базы. Формулы (23), (24) приводятся и в [21], где однако не оговаривается область их применения.

3. Разрешение на плоскости xOy

Наряду с разрешающей способностью системы по координатам x и y представляет интерес общий случай разрешения сигналов, рассеянных на объектах с произвольным взаимным расположением на плоскости xOy, из которого следовали бы формулы для  (13), (14) и  (19), (20). Исследование удобно провести с помощью построения в окрестности первого объекта области положений второго объекта (или области отклонений ,  второго объекта от первого), в которой объекты не разрешаются. В соответствии с (9) границы области для ,  можно найти из условия

 

                           (25)

или

 

и представить как функцию  (или ). С учетом (6) решения (25) имеют вид:

 

,                    (26)

.                  (27)

 

 

На рис. 6, 7 в качестве примера построены зависимости (26), (27), вычисленные для координат первого объекта ,  (рис. 6) и ,  (рис. 7). Остальные параметры движения объекта и системы взяты такими же как и ранее на рис. 2 ÷ 5.

 

 

Рис. 6.  Графики функций  и  (26), (27), вычисленные для координат первого объекта , , и ограничивающие область W,  в которой объекты не разрешаются

 

 

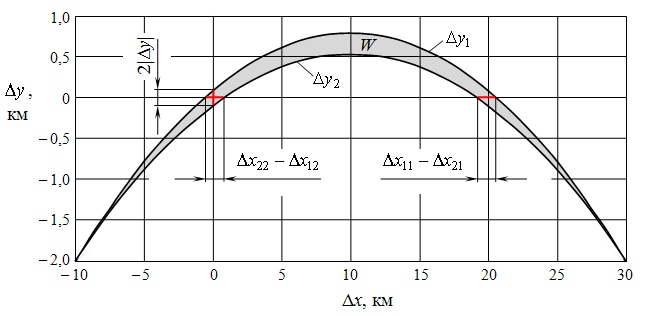
Рис. 7.  Графики функций  и  (26), (27), вычисленные для координат первого объекта ,

 

Функции  и  ограничивают область W, характеризуемую отклонениями координат второго объекта от первого, при которых разница доплеровских частот не превосходит величины  (11). Сечения области W прямыми  и  определяют разрешающую способность системы по координатам y и x соответственно: формулы (26), (27) при  сводятся к (13), (14), а при  – к (19), (20).

Аналогично (26), (27) из (25) можно получить и зависимости . Определенная для этого случая область W будет иметь такие же размеры (рис. 6, 7).

Составить наглядное представление о разрешающей способности РЛС позволяет расположение области W в системе координат xOy (рис. 1). Преобразование координат на рис. 6, 7 осуществляется сдвигом вдоль координатных осей области W на величину координат первого объекта ,  (рис. 6) и ,  (рис. 7). Это непосредственно следует из (26), (27), если координаты первого объекта обозначить как , а второго – . Тогда

,

 

и для границ области W в системе xOy (для координаты y второго объекта на границе W) из (26), (27) получаются выражения

 

,                         (28)

.                       (29)

 

 

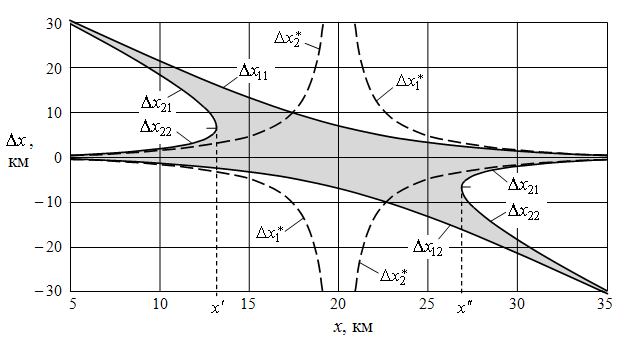
Зависимости (28), (29) для двух рассматриваемых на рис. 6, 7 случаев представлены на рис. 8, 9.

Следует отметить, что для точки (), симметричной положению  первого объекта относительно , область W будет иметь такой же вид. Например, построения для км, км приводят к тем же результатам, что показаны на рис. 8. для км,км.

Для объекта, находящегося на линии базы, область W область является двояковыпуклой и симметричной относительно оси Ox.

 

 

Рис. 8.  Область W в плоскости xOy

(координаты первого объекта , )

 

 

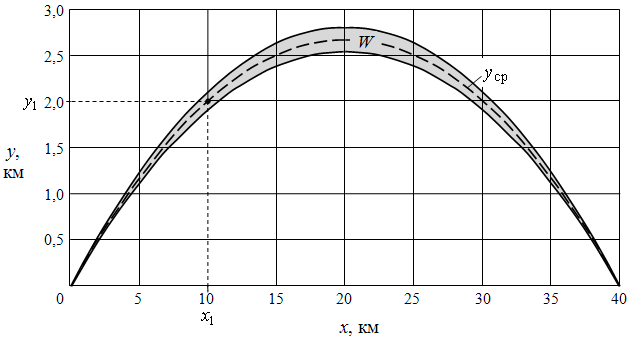
Рис. 9.  Область W в плоскости xOy

 (координаты первого объекта , )

 

Среднеарифметическое  от (28), (29) совпадает с зависимостью

 

,                                    (30)

 

получаемой из уравнения

 

 

и определяющей множество точек на плоскости xOy с одним и тем же значением доплеровской частоты . Зависимость (30) показана на рис. 8, 9 штриховой линией.

Сечения области W, построенной в координатах x, y, прямыми  и  определяют разрешение  и  вдоль координатных осей.

Сравнение рис. 8 и рис. 9 показывает, что при удалении объекта от линии базы область W становиться более выпуклой, что связано с квадратичной зависимостью функций (28) ÷ (30) от координаты x и ростом величины  с увеличением . Такое поведение области W приводит к повышению разрешения вдоль оси Ox по мере удаления от линии базы (в зоне видимости (1)), что было выявлено в разделе 2.

4. Другие случаи. Способы повышения разрешающей способности радиолокатора

В проведенном анализе остались неохваченными несколько случаев, требующих учета при построении просветных систем.

 а) Разрешение по высоте

Система практически не способна разрешать сигналы от объектов, движущихся на разных высотах над плоскостью xOy поперек линии базы, ввиду слабой зависимости доплеровской частоты от высоты полета h объектов [8]. Действительно, для малых y (1) и малых высот h, , , можно записать:

 

,     ,

,

 

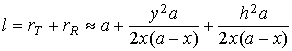откуда при  и  получается приближение (6):

 

.                       (31)

 

 

Аналогичным образом несложно показать, что разрешение отсутствует, если объекты двигаются под небольшим углом к плоскости xOy при неизменной разнице между их высотами.

 b) Влияния амплитудного детектирования на разрешение объектов

В системах с амплитудным детектированием принимаемого сигнала происходит “потеря” знака доплеровской частоты рассеянной радиоволны [6,11,17]. Как следствие при построении области W нужно иметь в виду ее симметричный относительно линии базы образ W', при попадании в который второго объекта рассеянные сигналы также не разрешаются. Пример такой ситуации показан на рис. 10. В момент времени, когда приближающийся к линии базы объект и удаляющийся от нее объект находятся на равном от линии базы расстоянии, доплеровские сдвиги частот рассеянных на объектах сигналов имеют одинаковую величину  (но противоположны по знаку; скорости объектов одинаковы). В этот момент второй объект находится в области W', и поэтому сигналы от объектов будут не разрешаемы.

Следует отметить, что границы областей W и W' совпадают в момент времени, когда объект пересекает линию базы. При удалении от линии базы перекрытие областей уменьшается. Ширина объединенной области достигает максимума  при  ( определяется из (13) или (14)). При  происходит разъединение областей.

 

 

Рис. 10. Пример взаимного положения объектов, сигналы от которых имеют

 одинаковую величину доплеровской частоты  и не разрешаются в системе с амплитудным детектированием

 

c) Повышение разрешающей способности

Используя разнесенный прием или направленную сканирующую приемную антенну можно добиться как разрешения сигналов в случаях а) и b), так и в целом повышения разрешающей способности просветного радиолокатора, в том числе в наиболее сложных случаях, когда сигналы от объектов на протяжении всего интервала наблюдения  имеют одинаковую частоту. К подобным случаям относятся перемещения объектов по траекториям, симметричным относительно линии базы, а также относительно прямой, проходящей через центр базы  перпендикулярно к ней [13,14].

Пример такой ситуации показан на рис. 11. Объекты движутся с равными скоростями по траекториям, симметричным относительно центра базы, имея в каждый момент времени одинаковые ординаты . Из (5), (6) видно, что доплеровские частоты сигналов совпадают, и на протяжении всего времени наблюдения  объекты находятся в области W. Разрешение сигналов можно получить за счет направленных свойств приемной антенны, используя разрешение по угловой координате (ΔΘ – ширина диаграммы направленности (ДН) приемной антенны, Δφ – разность угловых координат объектов, ).

 

 

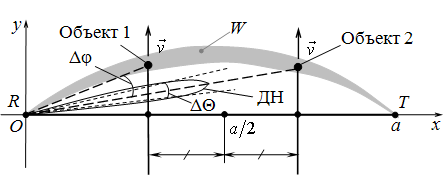
Рис. 11. Пример взаимного положения объектов,

разрешаемых по угловой координате 

 

Заключение

Проведенные исследования разрешающей способности просветного бистатического радиолокатора с монохроматическим излучением выявили ряд характерных особенностей, которые необходимо учитывать при построении просветных систем:

– Объекту, движущемуся в двухкоординатной радиолокационной системе (рис. 1), соответствует область W (рис. 8, 9), при попадании в которую другого объекта рассеянные на объектах сигналы не разрешаются по частоте. Область W расположена в окрестности линии, характеризуемой одинаковыми значениями доплеровской частоты; вытянута вдоль линии базы и  при удалении объекта от нее становится более выпуклой. Сечения области прямыми  и , проведенными через координаты объекта x, y, определяют интервалы разрешения  и  вдоль координатных осей, т.е. разрешающую способность РЛС по координатам.

 – Следствием вытянутости области W вдоль линии базы является существенно лучшая разрешающая способность системы по координате y, чем по координате x. Выпуклость и узость области W является причиной возможного возникновения второго интервала разрешения по x, расположенного симметрично к первому относительно центра базы  (рис. 4, 5).

В частном случае выбора интервала первичных измерений, исходя из скорости изменения доплеровской частоты, разрешение по координате y определяется радиусом первой зоны Френеля (15).

– Разрешение объектов по высоте практически отсутствует из-за слабой зависимости доплеровской частоты от высоты полета объектов (31).

– Отсутствует разрешение сигналов от объектов, если доплеровская частота рассеянных сигналов имеет одинаковую величину . Для разрешения сигналов в подобных ситуациях и в целом повышения разрешающей способности просветного радиолокатора, в том числе, когда объекты движутся параллельными курсами поперек линии базы и постоянно находятся в области W (рис. 11),  необходимо использовать направленные свойства антенн или переходить к построению систем с пространственно разнесенным приемом.

Литература

1. Уфимцев, П.Я. Основы физической теории дифракции. – М.: БИНОМ, 2011. – 351 c.

2. Бляхман, А.Б. Бистатическая эффективная площадь рассеяния и обнаружение объектов при радиолокации "на просвет" / А.Б. Бляхман, И.А. Рунова // Радиотехника и электроника. – 2001. – Т. 46, № 4. – С. 424 – 432.

3. Чапурский, В.В. Синтезированная теневая радиоголография в бистатической радиолокации // Радиотехника. – 2009. – № 3. – С. 52 – 69.

4. Радиолокационный способ определения параметров движения объекта: пат. 2133480 Рос. Федерация: МПК⁶ G01S3/72, G01S7/42 / Бляхман А.Б., Самарин А.В.; заявитель и патентообладатель Нижегород. науч.-исслед. ин-т радиотехники. – № 98101955/09; заявл. 02.02.98; опубл. 20.07.99.

5. Ковалев, Ф.Н. Фазовая пеленгация в системах радиолокации на просвет / Ф.Н. Ковалев, В.В. Кондратьев // Доклады Академии наук. – 2014. – Т. 455, № 4. – С. 401 – 403.

6. Ковалев, А.Н. Определение разности расстояний до движущегося объекта в просветных радиолокационных системах с разнесенным приемом / А.Н. Ковалев, Ф.Н. Ковалев // Известия высших учебных заведений. Радифизика. – 2014. – Т. LVII, № 6. – С. 491– 496.

7. Ковалев, Ф.Н. Интегральный доплеровский метод измерения угловых координат объекта в системах радиолокации на просвет // Журнал радиоэлектроники: электронный журнал. – 2013. – № 12. – URL: http://jre.cplire.ru/jre/dec13/13/text.pdf.

8. Ковалев, Ф.Н. Особенности угломерно-дальномерного метода определения местоположения цели в просветных бистатических радиолокаторах / Ф.Н. Ковалев, В.В. Кондратьев // Журнал радиоэлектроники: электронный журнал. – 2014. – № 4. – URL: http://jre.cplire.ru/jre/apr14/1/text.pdf.

9. Ковалев, Ф.Н. Определение координат цели методом максимального правдоподобия в просветной многопозиционной радиолокационной системе // Системы управления и информационные технологии. – 2013. – № 2.1 (52) – С. 128 – 132.

10. Ковалев, Ф.Н. Определение параметров траектории цели в просветных бистатических радиолокационных системах // Системы управления и информационные технологии. – 2013. – № 4 (54) – С. 86 – 90.

11. Ковалев, Ф.Н. Устранение неоднозначности измерений угловых координат фазовым методом в просветных радиолокаторах / Ф.Н. Ковалев, В.В. Кондратьев // Оборонный комплекс научно-техническому прогрессу России. – 2014. – № 3 (123). – С. 31 – 35.

12. Ковалев, А.Н. Определение момента пересечения объектом отрезка между приемником и передатчиком в системах радиолокации на просвет / А.Н. Ковалев, Ф.Н. Ковалев // Радиотехнические и телекоммуникационные системы. – 2013. – № 4(12). – С. 30 – 36.

13. Ковалев, Ф.Н. Определение координат движущихся целей по измерениям доплеровской частоты в радиолокационных системах с обнаружением "на просвет" // Радиотехника и электроника. – 2007. – Т. 52, № 3. – С. 331 – 339.

14. Ковалев, А.Н. Потенциальная точность определения параметров траектории цели в просветном бистатическом радиолокаторе / А.Н. Ковалев, Ф.Н. Ковалев // Труды Нижегородского государственного технического университета им. Р.Е. Алексеева. – 2014. – Т. 104, № 2. С. 17 – 22.

15. Реутов, А.П. Разрешающая способность обращенных радиоголограмм при регистрации рассеянного "вперед" поля / А.П. Реутов, В.В. Чапурский // Радиотехника. – 1987. – № 6. – С. 78 – 83.

16. Черняк, В.С. Многопозиционная радиолокация / В.С. Черняк. - М.: Радио и связь, 1993. - 416 с.

17. Теоретические основы радиолокации: учебное пособие для вузов / под ред. Я.Д. Ширмана. – М.: Сов. Радио, 1970. – 560 с.

18. Nezlin, D.V. Bistatic Radar. Principles and Practice / D.V. Nezlin [et al]; Ed. M. Cherniakov. – England: Wiley, 2007. – 504 p.

19. Ковалев, Ф.Н. Оптимизация первичных измерений в бистатической "просветной" РЛС // Науч.-техн. конф. факультета информационных систем и технологий, посвященная 80-летию Нижегородской радиолаборатории: тез. докл. - Н. Новгород: НГТУ, 1998. - С. 11 - 12.

20. Ковалев, А.Н. Статистические характеристики ошибок местоопределения цели в бистатической радиолокационной системе просветного типа / А.Н. Ковалев, Ф.Н. Ковалев // Известия высших учебных заведений. Радиоэлектроника. – 2014. – Т. 57, № 3. – С. 3 – 9.

21. Мякиньков, А.В. Пространственное разрешение целей в просветной РЛС с непрерывным зондирующим сигналом / А.В. Мякиньков, А.Г. Огурцов, А.Г. Рындык // Датчики и системы. – 2014. – № 11. – С. 11 – 15.