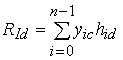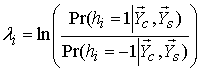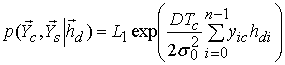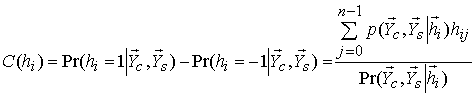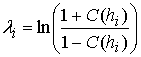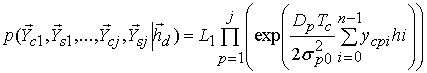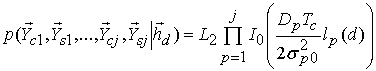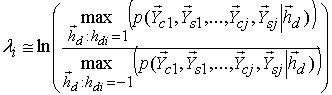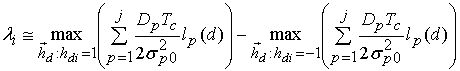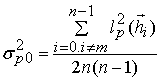УДК 621.391.01
АЛГОРИТМЫ ПОСИМВОЛЬНОГО ПРИЕМА СИГНАЛОВ С РАСШИРЕННЫМ СПЕКТРОМ В МНОГОЛУЧЕВЫХ КАНАЛАХ С ЧАСТОТНО-СЕЛЕКТИВНЫМИ ЗАМИРАНИЯМИ
Л. Е. Назаров 1, П. В. Шишкин 2
1Фрязинский филиал Института радиотехники и электроники им. В.А.Котельникова РАН, г. Фрязино
2АО «Информационные спутниковые системы» им. академика М.Ф.Решетнева, г. Железногорск
Статья поступила в редакцию 29 февраля 2016 г.
Аннотация. Приведены алгоритмы посимвольного приема сигналов с расширенным частотным спектром в виде базисных функций Уолша-Адамара, используемых при передаче информации по многолучевым каналам с частотно-селективными замираниями. Разработанные алгоритмы посимвольного приема основаны на использовании производительного алгоритма быстрого преобразования Уолша.
Ключевые слова: каналы передачи, многолучевость, частотно-селективные замирания, сигналы, посимвольный прием.
Abstract. The algorithms of symbol-by-symbol decoding for broad band signals propagated through multiple propagation paths (reflections from ionosphere, etc.) with frequency-selective fading are studied in the article. The base of these algorithms is Fast Hadamard Transformation.
Key words: multipath channels, frequency-selective fading, signals, symbol-by-symbol decoding.
Введение
Выбор эффективных сигнальных конструкций и методов их обработки, обеспечивающих надежную передачу информации, определяются свойствами и характеристиками физических каналов [1]. Базовой моделью является канал с аддитивным белым гауссовским шумом (АБГШ) [2,3]. Для многих физических каналов (каналы ионосферных и тропосферных систем связи, каналы наземных и спутниковых подвижных систем связи) наряду с АБГШ рассматривается многолучевость распространения сигналов [1-4].
Многолучевость обусловливает фазо-частотные и амплитудно-частотные искажения сигналов на входе приемных устройств и наличие межсимвольной интерференции (МСИ), приводящей к частотно-селективным и частотно-неселективным замираниям (мультипликативные помехи) [2].
Методы организации передачи информации с целью снижения влияния мультипликативных помех характеризуются большей сложностью по сравнению с методами передачи для АБГШ канала. Эти методы основаны на использовании разнесения сигналов (частотное, временное, пространственное); на применении процедур адаптивного выравнивания каналов; на использовании процедур нелинейной обработки сигналов с использованием алгоритма Витерби в сочетании с моделью импульсной характеристики канала; на использовании сигналов с расширенным спектром с разделением парциальных лучей и их когерентного или некогерентного комбинирования [2,3].
Эти методы используются в сочетании со схемами помехоустойчивого кодирования, для наиболее эффективных кодов разработаны алгоритмы с итеративным приемом (турбо-коды, низкоплотностные коды [5], турбо-подобные коды [6]). Данные алгоритмы основаны на использовании процедур посимвольного приема (вычисление “мягких” решений (многоразрядные квантованные)) относительно кодовых символов, которые необходимо вычислять с учетом многолучевого распространения сигналов. Это обусловливает актуальность разработки процедур вычисления “мягких” решений при реализации приведенных методов снижения эффективности многолучевости.
В статье приведены алгоритмы посимвольного приема сигналов с расширенным частотным спектром в виде базисных функций Уолша-Адамара, используемых при передаче информации по многолучевым каналам с частотно-селективными замираниями. Результирующие алгоритмы посимвольного приема основаны на использовании производительного алгоритма быстрого преобразования Уолша (БПУ) [7]. Даны результаты моделирования разработанных алгоритмов посимвольного приема.
1. Постановка задачи
Многолучевые каналы
описываются импульсной характеристикой ![]() или
коэффициентом передачи
или
коэффициентом передачи ![]() [2]. Для интервала локальной
стационарности сигнал
[2]. Для интервала локальной
стационарности сигнал ![]() на выходе канала для
передаваемого сигнала
на выходе канала для
передаваемого сигнала ![]() задается соотношением
задается соотношением
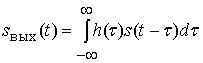 .
.
Интервал времени ![]() , в котором
, в котором ![]() существенно
отлична от 0, определяет память канала. Для канала дальней тропосферной связи
значение
существенно
отлична от 0, определяет память канала. Для канала дальней тропосферной связи
значение ![]() достигает 350…700 мксек [8]. Для канала
ионосферной связи при использовании антенн с узкой диаграммой направленности
достигает 350…700 мксек [8]. Для канала
ионосферной связи при использовании антенн с узкой диаграммой направленности ![]() не превышает 1…2 мксек, при использовании
антенн с расширенной диаграммой направленности максимальное значение
не превышает 1…2 мксек, при использовании
антенн с расширенной диаграммой направленности максимальное значение ![]() достигает 0.13…1 мсек [9]. Для сотовых систем
подвижной связи значения
достигает 0.13…1 мсек [9]. Для сотовых систем
подвижной связи значения ![]() достигают 20 мкс [10].
достигают 20 мкс [10].
Для сигналов ![]() с частотной полосой
с частотной полосой ![]() при условии
при условии ![]() наблюдаются
частотно-неселективные замирания [2,3]. В этом случае
наблюдаются
частотно-неселективные замирания [2,3]. В этом случае ![]() и влияние МСИ не учитывается,
и влияние МСИ не учитывается, ![]() - длительность
цифровых сигналов.
- длительность
цифровых сигналов.
При условии ![]() наблюдаются частотно-селективные
замирания, в этом случае
наблюдаются частотно-селективные
замирания, в этом случае ![]() и необходимо учитывать
влияние МСИ [2].
и необходимо учитывать
влияние МСИ [2].
Модель многолучевого
канала с частотно-селективными замираниями представляется дискретной линией
задержки с ![]() отводами и сумматором парциальных
сигналов
отводами и сумматором парциальных
сигналов ![]() с взвешивающими коэффициентами
с взвешивающими коэффициентами ![]() с отводов. Время задержки
с отводов. Время задержки ![]() ,
, ![]() .
.
Развитию этой модели для
каналов передачи со случайными импульсными характеристиками ![]() посвящен ряд работ [1-3].
посвящен ряд работ [1-3].
Один из эффективных
методов передачи для данного многолучевого канала основан на использовании
сигналов ![]() с расширенным частотным спектром
с расширенным частотным спектром ![]() , на выделении парциальных сигналов
, на выделении парциальных сигналов ![]() , соответствующих задержанным и взвешенным
копиям
, соответствующих задержанным и взвешенным
копиям ![]() в соответствии с моделью, и на их
объединении в приемных устройствах [2,3]. При достаточно точном оценивании
параметров сигналов
в соответствии с моделью, и на их
объединении в приемных устройствах [2,3]. При достаточно точном оценивании
параметров сигналов ![]() (оценивание задержек
(оценивание задержек ![]() и начальных фаз
и начальных фаз ![]() ,
амплитуд
,
амплитуд ![]() , доплеровских частот
, доплеровских частот ![]() ) возможно когерентное объединение. Более
простым является некогерентное объединение, не требующее оценки начальных фаз
) возможно когерентное объединение. Более
простым является некогерентное объединение, не требующее оценки начальных фаз ![]() [2].
[2].
В статье рассматриваются
сигналы с расширенным спектром, формируемые путем сопоставления ![]() информационным (кодовым) символам
дискретных базисных функций Уолша-Адамара объемом
информационным (кодовым) символам
дискретных базисных функций Уолша-Адамара объемом ![]() [7]. Коэффициент
частотного расширения (база сигналов) при организации передачи с когерентным
приемом равен
[7]. Коэффициент
частотного расширения (база сигналов) при организации передачи с когерентным
приемом равен ![]() . При организации передачи с
некогерентным приемом (ортогональность сигналов в усиленном смысле) коэффициент
частотного расширения равен
. При организации передачи с
некогерентным приемом (ортогональность сигналов в усиленном смысле) коэффициент
частотного расширения равен ![]() .
.
Суть задачи - разработка вычислительных процедур посимвольного приема информационных (кодовых) символов для многолучевого канала с частотно-селективными замираниями путем объединения (когерентного и некогерентного) парциальных сигналов с расширенным частотным спектром на основе базисных функций Уолша-Адамара.
2. Алгоритмы посимвольного приема для однолучевого канала
Ниже приведены алгоритмы обработки сигналов с расширенным частотным спектром при их посимвольном приеме для однолучевого канала распространения. Эти алгоритмы являются основой вычислительных процедур посимвольного приема сигналов для многолучевых каналов.
Пусть ![]() -
последовательность информационных символов (
-
последовательность информационных символов (![]() ),
которой однозначно сопоставляется дискретный сигнал
),
которой однозначно сопоставляется дискретный сигнал ![]() из
ансамбля базисных функций Уолша-Адамара объемом
из
ансамбля базисных функций Уолша-Адамара объемом ![]() и
длительностью
и
длительностью ![]() (
(![]() -
двоичное представление номера функции). Этот ансамбль дискретных сигналов
эквивалентен блоковому помехоустойчивому систематическому коду (
-
двоичное представление номера функции). Этот ансамбль дискретных сигналов
эквивалентен блоковому помехоустойчивому систематическому коду (![]() ), информационные символы расположены на
позициях
), информационные символы расположены на
позициях ![]() . Последовательности
. Последовательности ![]() равновероятны, рассматривается АБГШ канал
с односторонней спектральной плотностью
равновероятны, рассматривается АБГШ канал
с односторонней спектральной плотностью ![]() ,
передача осуществляется сигналами с двоичной фазовой манипуляцией.
,
передача осуществляется сигналами с двоичной фазовой манипуляцией.
Введем обозначения ![]() ,
, ![]() -
дискретные отсчеты для прямого и квадратурного каналов, соответствующие
символам функции Уолша-Адамара
-
дискретные отсчеты для прямого и квадратурного каналов, соответствующие
символам функции Уолша-Адамара ![]() с выхода сигнального
демодулятора при условии идеальной тактовой синхронизации,
с выхода сигнального
демодулятора при условии идеальной тактовой синхронизации,
![]() .
(2)
.
(2)
Здесь ![]() -
начальная фаза сигналов;
-
начальная фаза сигналов; ![]() - символы переданного
сигнала Уолша (
- символы переданного
сигнала Уолша (![]() );
); ![]() -
амплитуда сигналов;
-
амплитуда сигналов; ![]() - помеховые составляющие,
статистически независимые, с гауссовским законом распределения с нулевыми
средними и с дисперсиями
- помеховые составляющие,
статистически независимые, с гауссовским законом распределения с нулевыми
средними и с дисперсиями ![]() ;
; ![]() - длительность символов сигналов Уолша.
- длительность символов сигналов Уолша.
Если фаза ![]() или ее оценка известны, то можно положить
или ее оценка известны, то можно положить
![]() и реализуется когерентный прием с
использованием реализации
и реализуется когерентный прием с
использованием реализации ![]() , для неизвестной фазы
реализуется некогерентный прием с использованием реализаций
, для неизвестной фазы
реализуется некогерентный прием с использованием реализаций ![]() ,
, ![]() .
.
Процедуры приема “в целом” (когерентный и некогерентный), реализующие правило максимального правдоподобия, основаны на вычислении множества корреляционных соотношений [2]
Здесь ![]() -
символы функции Уолша-Адамара
-
символы функции Уолша-Адамара ![]() с номером
с номером ![]() .
.
Функция Уолша-Адамара ![]() , для которой достигается максимум в
множестве (
, для которой достигается максимум в
множестве (![]() ), соответствует переданному дискретному
сигналу для когерентного приема “в целом”. Функция Уолша-Адамара
), соответствует переданному дискретному
сигналу для когерентного приема “в целом”. Функция Уолша-Адамара ![]() , для которой достигается максимум в
множестве (
, для которой достигается максимум в
множестве (![]() ), соответствует переданному сигналу для
некогерентного приема “в целом”.
), соответствует переданному сигналу для
некогерентного приема “в целом”.
При посимвольном приеме вычисляются
“мягкие” решения ![]() , относительно символов
, относительно символов ![]() ,
, ![]() на
основе реализаций
на
основе реализаций ![]() ,
, ![]() [5]
[5]
При условии ![]() принимается решение
принимается решение ![]() , иначе
, иначе ![]() .
.
Апостериорные вероятности
![]() имеют вид
имеют вид
Для некогерентного приема
обозначение ![]() соответствует усредненной по
соответствует усредненной по ![]() условной плотности вероятности
условной плотности вероятности
Для когерентного приема имеем
Для некогерентного приема
после усреднения по ![]() имеем [11]
имеем [11]
Здесь 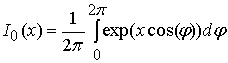 - модифицированная
функция Бесселя первого рода 0-го порядка;
- модифицированная
функция Бесселя первого рода 0-го порядка; ![]() - множители, не зависящие от
- множители, не зависящие от ![]() .
.
Таким образом, процедура
оценки апостериорных вероятностей ![]() заключается в
вычислении множества корреляций
заключается в
вычислении множества корреляций ![]() (3), (4), их нелинейном
преобразовании (8) для когерентного приема и (9) для некогерентного приема и
выполнении суммирования (6).
(3), (4), их нелинейном
преобразовании (8) для когерентного приема и (9) для некогерентного приема и
выполнении суммирования (6).
Вычисление ![]() выполняется с использованием алгоритма БПУ
размерностью
выполняется с использованием алгоритма БПУ
размерностью ![]() с операциями “сложение-вычитание-пересылки”.
Это повышает производительность обработки по отношению к прямому вычислению в
с операциями “сложение-вычитание-пересылки”.
Это повышает производительность обработки по отношению к прямому вычислению в ![]() раз [11]. Соотношение (6) также может
быть вычислено с использованием алгоритма БПУ размерностью
раз [11]. Соотношение (6) также может
быть вычислено с использованием алгоритма БПУ размерностью ![]() над сигналами (8) или (9) для когерентного или некогерентного
посимвольного приема [11]
над сигналами (8) или (9) для когерентного или некогерентного
посимвольного приема [11]
Числитель и знаменатель
(10) являются компонентами спектрального преобразования в базисе Уолша-Адамара.
Используя тождество ![]() , имеем результирующее выражение
, имеем результирующее выражение
Более простой метод
вычисления мягких решений ![]() , не требующий
вычисления функций экспоненциального вида, основан на применении приближенного
соотношения [5]
, не требующий
вычисления функций экспоненциального вида, основан на применении приближенного
соотношения [5]
В частности, для некогерентного посимвольного приема имеем
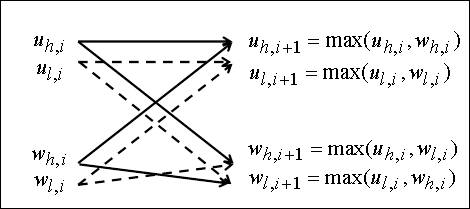
Рис.1. Схематическое изображение элемента (парная
“бабочка”) модифицированного алгоритма БПУ
с базовыми операциями
“сравнение-пересылки”.
При вычислении (12), (13)
применяется модифицированный алгоритм БПУ размерностью ![]() с
операциями “сравнение-пересылки” [6]. На рис.1 приведен вид элемента модифицированного
БПУ - “бабочки”
с
операциями “сравнение-пересылки” [6]. На рис.1 приведен вид элемента модифицированного
БПУ - “бабочки” ![]() -го слоя (
-го слоя (![]() ): выходные парные отсчеты
): выходные парные отсчеты ![]() и
и ![]() ,
являющиеся входными для
,
являющиеся входными для ![]() -го слоя, вычисляются
по правилам
-го слоя, вычисляются
по правилам
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Здесь ![]() и
и ![]() парные отсчеты на входе
парные отсчеты на входе ![]() -го слоя,
-го слоя, ![]() . На
первом слое отсчеты равны
. На
первом слое отсчеты равны ![]() ,
, ![]() ,
, ![]() , для
некогерентного приема имеем
, для
некогерентного приема имеем ![]() ,
, ![]() . На последнем
. На последнем ![]() -ом
слое определяются значения
-ом
слое определяются значения ![]() с использованием
соотношений (12), (13).
с использованием
соотношений (12), (13).
На рис.2 приведен граф
модифицированного БПУ размерностью ![]() .
.
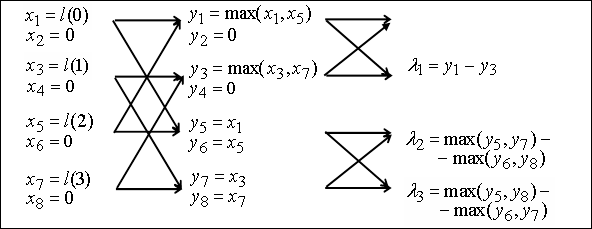
Рис.2. Результирующий граф модифицированного алгоритма
БПУ размерностью 4
с базовыми операциями “сравнение-пересылки”.
3. Алгоритмы посимвольного приема для каналов с многолучевостью
Для многолучевых каналов с
![]() парциальными лучами распространения
сигналов с расширенным частотным спектром рассматривается совокупность
парциальными лучами распространения
сигналов с расширенным частотным спектром рассматривается совокупность ![]() реализаций с выходов демодуляторов прямого
и квадратурного каналов (
реализаций с выходов демодуляторов прямого
и квадратурного каналов (![]() ).
).
Функция правдоподобия ![]() для когерентного приема имеет вид
для когерентного приема имеет вид
Для некогерентного приема
после усреднения по ![]() имеем [11]
имеем [11]
Здесь ![]() - множители, не зависящие от
- множители, не зависящие от ![]() ;
; ![]() ,
, ![]() -
амплитуда сигнальной составляющей и мощность помеховой составляющей для парциального
луча
-
амплитуда сигнальной составляющей и мощность помеховой составляющей для парциального
луча ![]() ; значения
; значения ![]() вычисляются
для парциальных лучей с использованием корреляционных соотношений (3), (4).
вычисляются
для парциальных лучей с использованием корреляционных соотношений (3), (4).
Апостериорные вероятности
![]() вычисляются на основе (14), (15) и
соотношения, подобного соотношению (10)
вычисляются на основе (14), (15) и
соотношения, подобного соотношению (10)
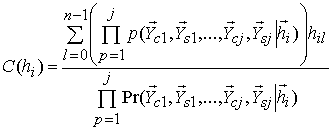 . (16)
. (16)
Вычисление “мягких”
решений ![]() с использованием значений
с использованием значений ![]() (16)
осуществляется с использованием соотношения (11).
(16)
осуществляется с использованием соотношения (11).
Более простой метод вычисления “мягких” решений основан на применении приведенного приближенного соотношения (12)
В частности, для некогерентного посимвольного приема имеем
При вычислении (17), (18)
может быть применен приведенный модифицированный алгоритм БПУ размерностью ![]() с операциями “сравнение-пересылки”.
с операциями “сравнение-пересылки”.
Для вычисления значений ![]() с
использованием (16), (17), (18) необходимо знание параметров
с
использованием (16), (17), (18) необходимо знание параметров 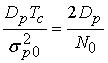 для парциальных лучей. Оценку данного
отношения можно произвести с использованием методики, приведенной в [11]. Обозначим
значение
для парциальных лучей. Оценку данного
отношения можно произвести с использованием методики, приведенной в [11]. Обозначим
значение ![]() , определяемое условием
, определяемое условием ![]() , выражения для
, выражения для  и
и
![]() имеют вид
имеют вид
4. Результаты вычислений
На рис.3 приведены
вероятностные характеристики (вероятности ошибки на бит ![]() )
когерентного и некогерентного приема ортогональных сигналов объемом
)
когерентного и некогерентного приема ортогональных сигналов объемом ![]() (число информационных битов
(число информационных битов ![]() ) для однолучевого канала АБГШ в
зависимости от отношения сигнал/помеха
) для однолучевого канала АБГШ в
зависимости от отношения сигнал/помеха ![]() .
Здесь
.
Здесь ![]() - энергия сигналов на информационный бит.
- энергия сигналов на информационный бит.
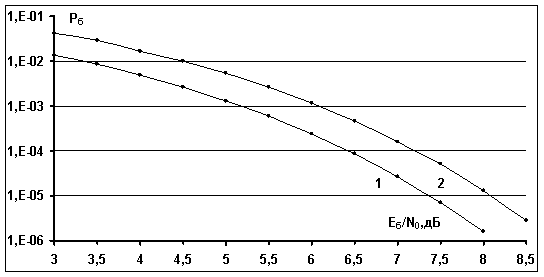
Рис.3. Вероятности ошибки на бит ![]() приема ортогональных сигналов объемом
приема ортогональных сигналов объемом ![]() для однолучевого канала АБГШ:
для однолучевого канала АБГШ:
1 –
когерентный прием; 2 – некогерентный прием.
Кривая 1 соответствует
когерентному приему “в целом”, в этом случае известно аналитическое выражение
для ![]() [1]
[1]
 . (21)
. (21)
Здесь  .
.
Кривая 2 соответствует
некогерентному приему “в целом”, в этом случае также известно аналитическое
выражение для ![]() [2]
[2]
 . (22)
. (22)
Видно, что для значения ![]() энергетический проигрыш для
некогерентного приема относительно когерентного приема достигает 1 дБ.
энергетический проигрыш для
некогерентного приема относительно когерентного приема достигает 1 дБ.
Вероятностные кривые для
оптимального посимвольного приема рассматриваемого ансамбля сигналов получены
путем компьютерного моделирования с использованием соотношений (6), (8)
(когерентный посимвольный прием) и (9) (некогерентный посимвольный прием).
Полученные вероятностные кривые незначительно отличаются от вероятностных
кривых приема “в целом”, приведенных на рис.1. Так для когерентного приема “в
целом” при  дБ имеем
дБ имеем ![]() , для
оптимального посимвольного приема имеем
, для
оптимального посимвольного приема имеем ![]() .
.
Моделирование алгоритмов
оптимального и подоптимального посимвольного приема с использованием
соотношений (17), (18) показало их эквивалентность относительно вероятностей
ошибки ![]() .
.
На рис.4 приведены
вероятностные характеристики когерентного и некогерентного посимвольного приема
рассматриваемых ортогональных сигналов объемом ![]() для
двухлучевого канала АБГШ. Вероятностные кривые получены путем компьютерного
моделирования алгоритмов посимвольного приема при условии равенства отношений
сигнал/помеха для парциальных лучей.
для
двухлучевого канала АБГШ. Вероятностные кривые получены путем компьютерного
моделирования алгоритмов посимвольного приема при условии равенства отношений
сигнал/помеха для парциальных лучей.
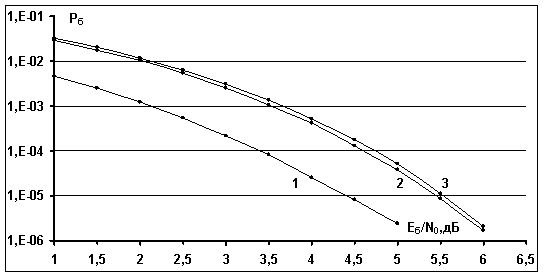
Рис.4. Вероятностные характеристики когерентного и
некогерентного посимвольного приема
ортогональных сигналов объемом ![]() (число информационных битов
(число информационных битов ![]() ) для двухлучевого канала АБГШ:
) для двухлучевого канала АБГШ:
1 –
оптимальный когерентный посимвольный прием: 2 – оптимальный некогерентный
посимвольный прием
3 – подоптимальный некогерентный посимвольный прием.
Кривая 1 соответствует
оптимальному когерентному посимвольному приему с использованием соотношений
(6), (14). Кривая 2 соответствует оптимальному некогерентному посимвольному
приему с использованием соотношений (6), (15). Видно, что для значения ![]() энергетический проигрыш для
некогерентного посимвольного приема относительно когерентного посимвольного
приема достигает 1 дБ.
энергетический проигрыш для
некогерентного посимвольного приема относительно когерентного посимвольного
приема достигает 1 дБ.
Моделирование показало,
что вероятностные кривые для алгоритмов подоптимального посимвольного приема с
использованием соотношения (12) незначительно отличаются от соответствующих
приведенных вероятностных кривых оптимального посимвольного приема. Так для
когерентного оптимального приема при 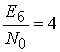 дБ имеем
дБ имеем ![]() , для подоптимального когерентного посимвольного
приема имеем
, для подоптимального когерентного посимвольного
приема имеем ![]() .
.
Кривая 3 соответствует подоптимальному некогерентному посимвольному приему с оценкой энергетических параметров
![]() ,
,
![]() ,
,
вычисляемых с использованием соотношений (19), (20) для лучей. Видно, что полученная кривая незначительно отличается от вероятностной кривой 2 для оптимального некогерентного посимвольного приема - энергетические потери не превышают 0.1 дБ.
Заключение
Приведены алгоритмы посимвольного когерентного и некогерентного приема сигналов с расширенным частотным спектром в виде ортогональных базисных функций Уолша-Адамара, используемых для передачи информации по многолучевым каналам с частотно-селективными замираниями. Приведенные алгоритмы реализуют оптимальный и подоптимальный (более простой относительно сложности реализации) посимвольный прием.
Даны результаты компьютерного моделирования разработанных алгоритмов посимвольного приема для однолучевого и двухлучевого канала АБГШ. Показано, что вероятностные кривые подоптимального посимвольного приема незначительно отличаются от соответствующих вероятностных кривых для оптимального посимвольного приема - отличия не превышают 0.1 дБ.
Разработка методов теоретического оценивания вероятностных характеристик посимвольного приема ансамблей сигналов составляет направление перспективных исследований.
Работа выполнена при поддержке РФФИ (№16-07-00746).
Литература
1. Зюко А.Г., Фалько А.И., Панфилов И.П., Банкет В.Л., Иващенко П.В. Помехоустойчивость и эффективность систем передачи информации. М.:Радио и связь. 1985.
2. Финк Л.М. Теория передачи дискретных сообщений. М.:Сов.радио. 1970.
3. Скляр Б. Цифровая связь. Теоретические основы и практическое применение. Перевод с англ. М.: Издательский дом “Вильямс”. 2003.
4. Феер К. Беспроводная цифровая связь. Методы модуляции и расширение спектра. Перевод с англ. под редакцией В.И.Журавлева. М.: Радио и связь. 2000.
5. Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. Перевод с англ. М.: Техносфера. 2005.
6. Назаров Л.Е., Головкин И.В. Последовательные турбо-коды с пониженной сложностью алгоритмов приема. // Радиотехника и электроника. 2010. Т. 55. №10. стр. 1193-1199.
7. Трахтман А.М., Трахтман В.А. Основы дискретных сигналов на конечных интервалах. М.: Советское радио. 1975.
8. Немировский А.С. Борьба с замираниями при передаче аналоговых сигналов. М.:Радио и связь. 1984.
9. Сорочинский М.В., Кузнецов О.О., Назаров Л.Е. Некоторые модели каналов передачи сигналов и экспериментальное определение их параметров. // Электронная техника. Выпуск 2(482). 2003. С.119-124.
10. Волков Л.Н., Немировский М.С., Шинаков Ю.С. Системы цифровой радиосвязи. Базовые методы и характеристики. М.:Экотрендз. 2005.
11. Назаров Л.Е. Некогерентный посимвольный прием сигналов, соответствующих двоичным блоковым кодам. // Радиотехника и электроника. 2003. Т.48. N7. С.818-823.