|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 5, 2002 |
|
Фильтрация сигналов при оценке частотно-временных параметров
Патюков В. Г., е-mail: pvg@fromru.com
Красноярский Государственный технический университет.
Получена 26.05.2003 г.
Рассматриваются эффективные алгоритмы получения оценок среднего значения частотно-временных параметров на примере аддитивной смеси гармонического сигнала и случайного узкополосного процесса. Раскрывается механизм формирования погрешностей на основе теории обобщённого корреляционного анализа. Приводятся алгоритмы построения усредняющих устройств, эффективность которых сопоставима с максимально правдоподобными оценками.
В теории связи, навигации, радио и гидролокации, в системах синхронизации и управления и при решении многих других задач требуется получать и использовать оценки частотно-временных параметров и, следовательно, измерять частоту, период или фазу исследуемых сигналов. При этом точность и помехоустойчивость работы всей системы зависит от эффективности используемых алгоритмов при обработке сигналов и достигаемой минимизации погрешностей оценок частотно-временных параметров. Теоретически потенциальными являются оценки, полученные на основе метода максимума функции правдоподобия, но их реализация приводит к сложным корреляционным и многоканальным устройствам [1-3]. Поэтому на практике широкое распространение получили устройства, использующие упрощённые алгоритмы работы, повышение эффективности которых и составляет основной предмет исследования. Наиболее часто оценки частотно–временных параметров сигналов на практике реализуют цифровыми устройствами [4,5], которые обеспечивают фильтрацию исследуемого сигнала и формируют среднеинтегральную оценку результата усреднения. Повышение точности и помехоустойчивости таких устройств, при различных условиях работы, является важной задачей исследований.
Фильтрацию сигналов при оценке частотно–временных параметров рассмотрим на примере широко распространённой модели, представляющей собой аддитивную смесь гармонического сигнала и случайного узкополосного процесса:
![]()
где ![]() ,
, ![]() и
и ![]() -
амплитуда, угловая частота и начальная фаза сигнала
-
амплитуда, угловая частота и начальная фаза сигнала ![]() ;
; ![]() и
и ![]() -
огибающая и фаза случайного процесса
-
огибающая и фаза случайного процесса ![]() ;
; ![]() и
и ![]() -
огибающая, случайная фаза и полная фаза аддитивной смеси. Одним из основных
параметров, оценку среднего значения, которого необходимо найти, является
мгновенная частота, связанная с полной фазой известным соотношением
-
огибающая, случайная фаза и полная фаза аддитивной смеси. Одним из основных
параметров, оценку среднего значения, которого необходимо найти, является
мгновенная частота, связанная с полной фазой известным соотношением ![]() , где
, где ![]() - случайная частота, определяемая через производную фазы
исследуемой аддитивной смеси и характеризующая скорость её изменения. Случайная
частота исследуемого сигнала, определяет шумовую составляющую суммарной погрешности
оценки среднего значения мгновенной частоты, а характер изменения её спектрально-корреляционных
характеристик существенно влияет на дисперсию результата усреднения.
- случайная частота, определяемая через производную фазы
исследуемой аддитивной смеси и характеризующая скорость её изменения. Случайная
частота исследуемого сигнала, определяет шумовую составляющую суммарной погрешности
оценки среднего значения мгновенной частоты, а характер изменения её спектрально-корреляционных
характеристик существенно влияет на дисперсию результата усреднения.
При нахождении
оценок среднего значения мгновенной частоты, последние зависят как от
быстротечности изменения параметров исследуемой аддитивной смеси, так и от
характеристик обрабатывающего фильтра. Быстротечность протекания процесса во
временной области характеризуется корреляционной функцией, а основной
характеристикой обрабатывающего фильтра (усредняющего устройства) является
импульсная характеристика или её преобразование Фурье. В классе линейных оценок
частотно-временных параметров сигналов при обработке случайного процесса ![]() и усреднении на
временном интервале
и усреднении на
временном интервале ![]() , воспользуемся классической
операцией вычисления среднего значения:
, воспользуемся классической
операцией вычисления среднего значения:
где ![]() -
знак математического ожидания, а
-
знак математического ожидания, а ![]() -
импульсная характеристика обрабатывающего фильтра, удовлетворяющая условию несмещённости
оценки
-
импульсная характеристика обрабатывающего фильтра, удовлетворяющая условию несмещённости
оценки ![]() .
.
Корреляционную функцию погрешности оценки среднего значения мгновенной частоты можно получить с учётом преобразования о спектре свёртки [6]:
где ![]() и
и ![]() -
энергетический спектр и корреляционная функция усредняемой реализации
случайного процесса
-
энергетический спектр и корреляционная функция усредняемой реализации
случайного процесса ![]()
![]() и
и ![]() – квадрат модуля передаточной
функции обрабатывающего фильтра и “корреляционная функция” импульсной характеристики
обрабатывающего фильтра, характеризующая скорость её изменения. Следовательно,
корреляционная функция погрешности оценки математического ожидания представляет
собой свёртку корреляционных функций исследуемого процесса и фильтра, а
дисперсия погрешности оценки подлежит оптимизации в соответствии с выражением [7]:
– квадрат модуля передаточной
функции обрабатывающего фильтра и “корреляционная функция” импульсной характеристики
обрабатывающего фильтра, характеризующая скорость её изменения. Следовательно,
корреляционная функция погрешности оценки математического ожидания представляет
собой свёртку корреляционных функций исследуемого процесса и фильтра, а
дисперсия погрешности оценки подлежит оптимизации в соответствии с выражением [7]:
при различных моделях
энергетических спектров исследуемых процессов ![]() и амплитудно-частотных характеристик используемых
фильтров.
и амплитудно-частотных характеристик используемых
фильтров.
Эффективность оценок математического ожидания определяется величиной дисперсии, механизм формирования которой и возможности минимизации, выявляются при анализе графиков поверхности обобщённых корреляционных функций устройств обработки исследуемых сигналов. Введём и оптимизируем обобщённую двумерную корреляционную функцию обрабатывающего фильтра [8, 9]:
где ![]() -
временное смещение, а
-
временное смещение, а ![]() - смещение по частоте. Поверхность, образуемая
на частотно-временной плоскости функцией
- смещение по частоте. Поверхность, образуемая
на частотно-временной плоскости функцией ![]() характеризует погрешность оценки среднего
значения мгновенной частоты и даёт возможность оценить эффективность используемой
фильтрации. Анализ обобщённой корреляционной функции усредняющего устройства
позволяет произвести необходимую оптимизацию параметров весовой функции и согласовать
частотно-временные характеристики обрабатывающего фильтра с характеристиками
усредняемого случайного процесса
характеризует погрешность оценки среднего
значения мгновенной частоты и даёт возможность оценить эффективность используемой
фильтрации. Анализ обобщённой корреляционной функции усредняющего устройства
позволяет произвести необходимую оптимизацию параметров весовой функции и согласовать
частотно-временные характеристики обрабатывающего фильтра с характеристиками
усредняемого случайного процесса ![]() .
.
Простейшей
классической весовой обработкой результатов оценки частотно-временных
параметров является оценка с равными весами (или с весовой функцией Дирихле
[10]),
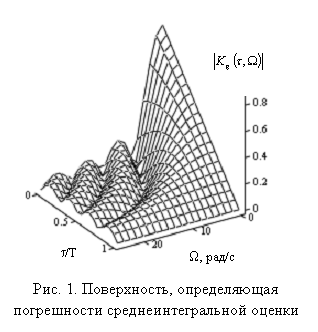
которую можно получить из (1) при ![]() . В соответствии с (4), полученный фрагмент
графика поверхности обобщённой корреляционной функции усредняющего устройства,
определяющего погрешности среднеинтегральной оценки, широко используемой при
сглаживании случайных процессов с различными моделями
энергетических спектров, приведён на рис. 1. Характерные сечения графика
рассматриваемой поверхности при различных значениях параметров, даны на
рис. 2.
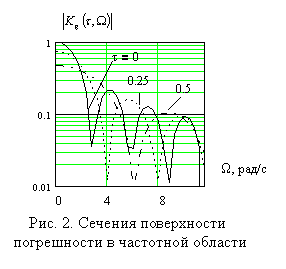
В соответствии с представленными графиками следует, что сечение поверхности при
. В соответствии с (4), полученный фрагмент
графика поверхности обобщённой корреляционной функции усредняющего устройства,
определяющего погрешности среднеинтегральной оценки, широко используемой при
сглаживании случайных процессов с различными моделями
энергетических спектров, приведён на рис. 1. Характерные сечения графика
рассматриваемой поверхности при различных значениях параметров, даны на
рис. 2.
В соответствии с представленными графиками следует, что сечение поверхности при
![]() характеризует
уровень дисперсии среднеинтегральной оценки, так как представляет собой
преобразование Фурье импульсной характеристики и, согласно (3), определяет величину
дисперсии оценки. Уменьшение дисперсии оценки в этом случае возможно лишь с
увеличением времени усреднения, в результате этого минимумы
характеризует
уровень дисперсии среднеинтегральной оценки, так как представляет собой
преобразование Фурье импульсной характеристики и, согласно (3), определяет величину
дисперсии оценки. Уменьшение дисперсии оценки в этом случае возможно лишь с
увеличением времени усреднения, в результате этого минимумы ![]() смещаются к началу координат графика
поверхности, характеризующей погрешность результата усреднения, ограничивая
влияние помех на оценку математического ожидания (рис. 2).
смещаются к началу координат графика
поверхности, характеризующей погрешность результата усреднения, ограничивая
влияние помех на оценку математического ожидания (рис. 2).
Использование и оптимизация различных весовых функций позволяет существенно уменьшить дисперсию оценки результатов статистического усреднения, но возникают сложности при реализации. Высокоэффективные оценки частотно-временных параметров сигналов могут быть получены при использовании гибкой модели весовых функций вида:
где ![]() - параметр весовой функции, изменение
которого позволяет получать различные частные значения амплитудно-частотных
характеристик усредняющего устройства:
- параметр весовой функции, изменение
которого позволяет получать различные частные значения амплитудно-частотных
характеристик усредняющего устройства:
![]() ,
,
где ![]()
![]() -
функция вида
-
функция вида ![]() а
а
![]() - параметр, позволяющий изменять вид
- параметр, позволяющий изменять вид ![]() , и, например при
, и, например при ![]() получить
среднеинтегральную оценку в усредняющем устройстве с импульсной характеристикой,
равной
получить
среднеинтегральную оценку в усредняющем устройстве с импульсной характеристикой,
равной ![]()
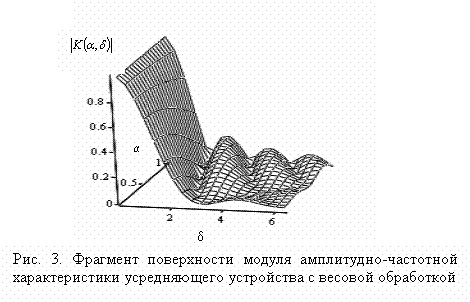
Общие выводы об
эффективности такой обработки можно получить из графика поверхности  представленной на
рис.
3.
представленной на
рис.
3.
Анализируя
поведение поверхности на частотно-временной плоскости, можно отметить, что вид
сечений поверхности, выполненных параллельно нормированной оси 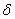 при различных
фиксированных значениях параметра
при различных
фиксированных значениях параметра 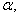 представляют собой графики модулей
амплитудно-частотных характеристик различных фильтров, зависящих как от вида
импульсной характеристики усредняющего устройства (параметра
представляют собой графики модулей
амплитудно-частотных характеристик различных фильтров, зависящих как от вида
импульсной характеристики усредняющего устройства (параметра 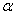 ), так и от времени
усреднения
), так и от времени
усреднения 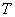 ,
увеличение которого позволяет уменьшить флуктуации оценки математического ожидания
случайного процесса до необходимого уровня. Кроме того, появляется
дополнительная возможность изменять частичный объём, ограниченный поверхностью
центрального пика функции
,
увеличение которого позволяет уменьшить флуктуации оценки математического ожидания
случайного процесса до необходимого уровня. Кроме того, появляется
дополнительная возможность изменять частичный объём, ограниченный поверхностью
центрального пика функции 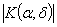 при постоянном
при постоянном 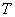 . Эта функция, в соответствии с (3),
непосредственно влияет на величину дисперсии оценки среднего значения мгновенной
частоты.
. Эта функция, в соответствии с (3),
непосредственно влияет на величину дисперсии оценки среднего значения мгновенной
частоты.
В зависимости
от ![]() уровень
пиков боковых лепестков функции
уровень
пиков боковых лепестков функции ![]() изменяется от минус 14 дБ при
изменяется от минус 14 дБ при ![]() до минус 27 дБ при
до минус 27 дБ при ![]() Одновременно с
уменьшением уровня пиков боковых лепестков наблюдается расширение центрального
лепестка. Значение поверхности при
Одновременно с
уменьшением уровня пиков боковых лепестков наблюдается расширение центрального
лепестка. Значение поверхности при ![]() равно
равно ![]() Этот результат получается из условия
нормировки, если выполнить преобразования:
Этот результат получается из условия
нормировки, если выполнить преобразования:
![]()
где
![]() –
дельта-функция в частотной области.
–
дельта-функция в частотной области.
“Энергетический” параметр импульсной характеристики для обобщённой весовой функции (5) будет равен:
![]()
и график, характеризующий его изменения, приведён на
рис. 4. При ![]() (равномерная
весовая функция)
(равномерная
весовая функция) ![]() ,
а при
,
а при ![]() (треугольная
весовая функция)
(треугольная
весовая функция) ![]() График
характеризует эффективность весовой обработки по отношению к равномерной
весовой функции при единичном значении времени усреднения, а экстремум
соответствует значению
График
характеризует эффективность весовой обработки по отношению к равномерной
весовой функции при единичном значении времени усреднения, а экстремум
соответствует значению ![]()
Используя метод неопределённых множителей Лагранжа, в работе [11] получен алгоритм, обеспечивающий минимум дисперсии погрешности по дискретной выборке, который во временной области является оптимальной импульсной характеристикой устройства обработки сигнала при оценке частотно-временных параметров /12/:
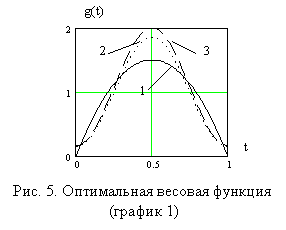
График, характеризующий вид функции (6), приведён на рис. 5 (график 1) совместно с другими известными [8,10] весовыми функциями - Ханна (график 2) и Хемминга (график 3), обладающими высокой эффективностью подавления помех [9]. Для всех рассматриваемых моделей весовых функций выполнены условия нормировки, обеспечивающие несмещенность оценки среднего значения мгновенной частоты.
Сглаживание и фильтрация случайных процессов, в общем, и оценка математического ожидания мгновенной частоты, в частности, с оптимальной весовой функцией (рис. 5), кроме высокой эффективности, обеспечивающей минимизацию дисперсии погрешности результата усреднения до её предельного значения, имеет ещё и то важное достоинство, что эта функция наилучшим образом может быть аппроксимирована при переходе к дискретной обработке результатов усреднения [11]. Другие весовые функции, в частности, приведённые на рис. 5, имеют сложный характер изменения, который при переходе к дискретной обработке не удаётся аппроксимировать простыми дискретными функциями с равными “ступенями”.
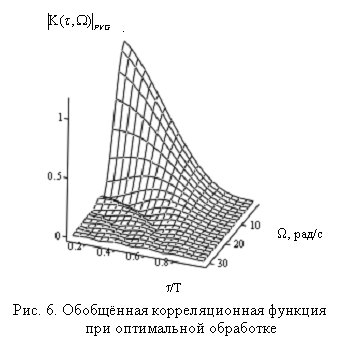
На
рис. 6
приведён график поверхности обобщённой корреляционной функции усредняющего
устройства ![]() ,
полученный при использовании оптимальной весовой обработки сигнала с
использованием формулы (6), а на рис. 7 для сравнения представлена обобщённая корреляционная
функция Бартлетта -
,
полученный при использовании оптимальной весовой обработки сигнала с
использованием формулы (6), а на рис. 7 для сравнения представлена обобщённая корреляционная
функция Бартлетта - ![]() , представляющая свёртку двух функций
Дирихле с равными весами половинной длительности. Приведенные графики получены
в результате моделирования на основе теории обобщённого корреляционного
анализа, и имеют существенно меньший уровень боковых лепестков по сравнению с
погрешностями, получаемыми при среднеинтегральной оценке, график поверхности
которой, приведён на рис. 1.
, представляющая свёртку двух функций
Дирихле с равными весами половинной длительности. Приведенные графики получены
в результате моделирования на основе теории обобщённого корреляционного
анализа, и имеют существенно меньший уровень боковых лепестков по сравнению с
погрешностями, получаемыми при среднеинтегральной оценке, график поверхности
которой, приведён на рис. 1.
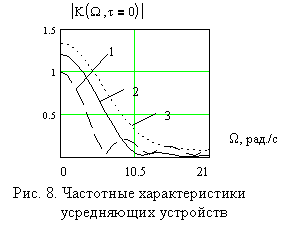
На
рис. 8
представлены значения графиков поверхностей обобщённых корреляционных функций в
частотной области, позволяющие оценить степень эффективности статистической
обработки результатов усреднения при классической обработке с равными весами,
весовых функций (6) и Бартлетта. Весовая функция Бартлетта получается в частном
случае обработки сигнала с весовой функцией (5) при значении параметра ![]() и обладает высокой
эффективностью фильтрации.
и обладает высокой
эффективностью фильтрации.
Так, в
соответствии с графиками, приведенными на рис. 8 можно сделать вывод, что при ![]() график 2,
характеризующий весовую функцию (6), имеет самый низкий уровень боковых
лепестков. Первый боковой лепесток при равномерной весовой обработке (график 1)
находится на уровне минус 13.8 дБ, а для графика 2 этот уровень равен минус
20.9 дБ. Значение боковых лепестков функции Бартлетта при этом составляет минус
16.8 дБ (график 3).
график 2,
характеризующий весовую функцию (6), имеет самый низкий уровень боковых
лепестков. Первый боковой лепесток при равномерной весовой обработке (график 1)
находится на уровне минус 13.8 дБ, а для графика 2 этот уровень равен минус
20.9 дБ. Значение боковых лепестков функции Бартлетта при этом составляет минус
16.8 дБ (график 3).
Следовательно,
низкий уровень боковых лепестков и концентрация объёма обобщённой
корреляционной функции ![]() в начале координат частотно-временной
плоскости обеспечивают высокую эффективность полученной весовой функции.
в начале координат частотно-временной
плоскости обеспечивают высокую эффективность полученной весовой функции.
На основе проведённых исследований разработаны различные устройства статистической обработки результатов промежуточных оценок частотно-временных параметров сигналов [13–17].
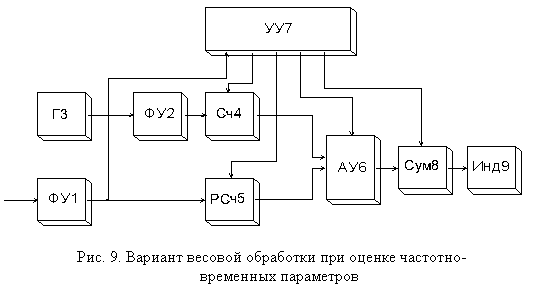
Обобщённая структурная схема возможного варианта построения усредняющего устройства представлена на рис. 9 [17]. Одним из основных узлов при построении таких устройств является формирователь выбранной весовой функции, который может быть реализован в соответствии с формулой (5) или (6), а также преобразователь промежуточных результатов усреднения.
Это устройство
оценки среднего значения мгновенной частоты работает в режиме измерения
периода, которые образуются потоком импульсов на выходе формирующего устройства
ФУ1, соответствующих моментам перехода аддитивной смеси гармонического
сигнала и шума через нулевой уровень. Эти импульсы поступают на реверсивный счётчик
РСч5, подсчитывающий число периодов, и на устройство управления УУ7.
Реверсивный счётчик совместно с УУ7 и арифметическим устройством АУ6
формируют необходимую весовую функцию ![]() с выбранным параметром
с выбранным параметром ![]() . С помощью генератора Г3,
ФУ2, счётчика Сч4 и УУ7 выполняется дискретизация первого
периода исследуемого сигнала. Результат измерения первого периода (Т1)
умножается в АУ6 на единицу и результат умножения переписывается в
сумматор 8. Счётчик 4 сбрасывается на нуль и производится оценка значения
второго периода. Результат оценки Т2 умножается в АУ6
на два и переписывается в сумматор. Счётчик 4 сбрасывается на нуль и осуществляется
оценка третьего периода. Если использовать весовую функцию Бартлетта (
. С помощью генератора Г3,
ФУ2, счётчика Сч4 и УУ7 выполняется дискретизация первого
периода исследуемого сигнала. Результат измерения первого периода (Т1)
умножается в АУ6 на единицу и результат умножения переписывается в
сумматор 8. Счётчик 4 сбрасывается на нуль и производится оценка значения
второго периода. Результат оценки Т2 умножается в АУ6
на два и переписывается в сумматор. Счётчик 4 сбрасывается на нуль и осуществляется
оценка третьего периода. Если использовать весовую функцию Бартлетта (![]() ), то описанные операции
нужно повторить до среднего из
), то описанные операции
нужно повторить до среднего из ![]() усредняемых периодов, а затем с помощью УУ7
и реверсивного счётчика 5 с каждым последующим периодом происходит уменьшение
коэффициента умножения на единицу. Таким образом, равноотстоящие от середины
периоды входного сигнала, результат квантования которых фиксируется в счётчике
4, умножается в АУ6 на одинаковое число. Результат усреднения случайных
периодов накапливается в сумматоре 8 и индицируется в 9.
усредняемых периодов, а затем с помощью УУ7
и реверсивного счётчика 5 с каждым последующим периодом происходит уменьшение
коэффициента умножения на единицу. Таким образом, равноотстоящие от середины
периоды входного сигнала, результат квантования которых фиксируется в счётчике
4, умножается в АУ6 на одинаковое число. Результат усреднения случайных
периодов накапливается в сумматоре 8 и индицируется в 9.
Погрешность работы
устройства при оценке среднего периода будет снижена по сравнению с равномерной
весовой обработкой, в ![]() раза,
где
раза,
где ![]() - эффективная ширина энергетического спектра
флуктуаций и отличается от оценок, полученных по методу максимума функции
правдоподобия на 0.5 дБ [18]. Так, например при Т=1с и
- эффективная ширина энергетического спектра
флуктуаций и отличается от оценок, полученных по методу максимума функции
правдоподобия на 0.5 дБ [18]. Так, например при Т=1с и ![]() Гц уменьшение дисперсии
оценки, по сравнению с классическим усредняющим устройством оценки периода,
составит
Гц уменьшение дисперсии
оценки, по сравнению с классическим усредняющим устройством оценки периода,
составит ![]() раза.
Кроме того, покажем, что в рассмотренном устройстве одновременно достигается
существенное снижение погрешности дискретности. Количество импульсов,
накопленные в сумматоре 8, в результате усреднения равно:
раза.
Кроме того, покажем, что в рассмотренном устройстве одновременно достигается
существенное снижение погрешности дискретности. Количество импульсов,
накопленные в сумматоре 8, в результате усреднения равно:
где ![]() -
результат заполнения счётными импульсами
-
результат заполнения счётными импульсами ![]() -го периода исследуемого сигнала;
-го периода исследуемого сигнала; ![]() - количество счётных импульсов в
- количество счётных импульсов в ![]() -м периоде;
-м периоде; ![]() период следования счётных импульсов;
период следования счётных импульсов; ![]() весовой коэффициент
весовой коэффициент ![]() -го результата усреднения.
-го результата усреднения.
Среднее значение периода исследуемого сигнала будет равно:
Определим математическое ожидание (8):
![]()
и, следовательно, вычисленный
устройством средний период соответствует истинному значению периода
исследуемого сигнала ![]() , то есть оценка периода несмещённая.
, то есть оценка периода несмещённая.
Найдём дисперсию
![]() ,
обусловленную погрешностью дискретности:
,
обусловленную погрешностью дискретности:
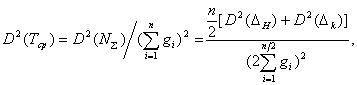
где ![]() -
дисперсия погрешности дискретности «начала» операции усреднения, а
-
дисперсия погрешности дискретности «начала» операции усреднения, а ![]() - дисперсия погрешности «конца» [19]. Поскольку дисперсия оценки
одного периода равна
- дисперсия погрешности «конца» [19]. Поскольку дисперсия оценки
одного периода равна ![]() [4],
то, полагая погрешности
[4],
то, полагая погрешности ![]() и
и ![]() независимыми и
независимыми и ![]() , в результате получим:
, в результате получим:
![]() .
.
Здесь учтено, что
![]()
![]() .
.
![]()
Чтобы оценить эффективность весовой обработки при снижении дисперсии погрешности дискретности составим отношение:
где ![]() -
дисперсия
-
дисперсия ![]() классического
устройства оценки среднего значения мгновенной частоты. Из (9) следует, что
среднеквадратическое значение погрешности дискретности уменьшается в ~
классического
устройства оценки среднего значения мгновенной частоты. Из (9) следует, что
среднеквадратическое значение погрешности дискретности уменьшается в ~ ![]() раз.
Так, например, при частоте квантования 10 МГц максимальная погрешность
дискретности классического устройства равна
раз.
Так, например, при частоте квантования 10 МГц максимальная погрешность
дискретности классического устройства равна ![]() , а среднеквадратическое значение
погрешности равно
, а среднеквадратическое значение
погрешности равно ![]() .
В устройствах с весовой обработкой, при той же частоте квантования и
.
В устройствах с весовой обработкой, при той же частоте квантования и ![]() , среднеквадратическое
значение погрешности дискретности окажется равным
, среднеквадратическое
значение погрешности дискретности окажется равным ![]() , то есть уменьшается в 50 раз. Такое же
значение погрешности дискретности можно получить и в классическом усредняющем устройстве,
но при частоте квантования
, то есть уменьшается в 50 раз. Такое же
значение погрешности дискретности можно получить и в классическом усредняющем устройстве,
но при частоте квантования ![]() МГц, то есть, связано с увеличением
частоты квантования в 50 раз и может быть реализовано только при использовании
быстродействующей элементной базы.
МГц, то есть, связано с увеличением
частоты квантования в 50 раз и может быть реализовано только при использовании
быстродействующей элементной базы.
Литература.
1. Куликов Е.И., Трифонов А. П. Оценка параметров сигналов на фоне помех. - М.: Сов. радио, 1978. - 296 с.
2. Тихонов В.И. Оптимальный приём сигналов. - М.: Радио и связь, 1983. - 320 с.
3. Тихонов В.И., Харисов В. Н. Статистический анализ и синтез радиотехнических устройств и систем. - М.: Радио и связь, 1991. - 608 с.
4. Ермолов Р.С. Цифровые частотомеры. - Л.: Энергия, 1973. - 152 с.
5. Аппаратура для частотных и временных измерений / Под ред. А.П. Горшкова. - М.: Сов. радио, 1971. - 336 с.
6. Гоноровский И.С. Радиотехнические цепи и сигналы. - М.: Радио и связь, 1986. - 510 с.
7. Патюков В.Г. Фильтрация флуктуаций при измерении частотно-временных параметров сигналов / Системные проблемы качества, математического моделирования, информационных, электронных и лазерных технологий / Материалы Международной конференции, Российской научной школы и Российского научного симпозиума. - М.: Радио и связь, 2002. - Ч. 4. - С. 133-136.
8. Кук Ч., Бернфельд М. Радиолокационные сигналы. - М.: Сов. Радио, 1971. - 568 с.
9. Патюков В.Г. Исследование погрешностей усредняющих устройств на основе обобщённого корреляционного анализа / Системные проблемы качества, математического моделирования и информационных технологий / Материалы международной научно-технической конференции и Российской научной школы. - М.: НИИ « Автоэлектроника», 2000. - С. 87-90.
10. Гутников В.С. Фильтрация измерительных сигналов. - Л.: Энергоатомиздат, 1990. - 192 с.
11. Патюков В.Г., Чмых М.К. Оптимальный алгоритм цифрового измерения частоты. // Известия ВУЗов, Приборостроение. - 1976. - № 3. - С. 21-24.
12. Patyukov V.G. Filtration of Signals at Time-and-Frequency Measurements / 6-th International Conference on Actual Problems of Electronic Instrument Engineering Proceedings. APEIE-2002. / IEEE Catalog Number: 02 EX546. V. 1. - Novosibirsk, 2002. - P. 108-109.
13. А. с. 1247771 SU, G 01 R 23/00. Цифровой частотомер / В.Г. Патюков. - Опубл. 30.07.86, Бюл. №28.
14. А. с. 1293664 SU, G 01 R 23/02. Цифровой частотомер / В.Г. Патюков. - Опубл. 28.02.87, Бюл. № 8.
15. А. с. 1366962 SU, G 01 R 23/10. Цифровой измеритель периода / В.Г. Патюков. - Опубл. 15.01.88, Бюл. № 2.
16. А. с. 1448295 SU, G 01 R 23/00. Цифровой частотомер / В.Г. Патюков. - Опубл. 30.12.88, Бюл. № 48.
17. А. с. 615429 СССР, МКИ2 G 01 R 29/02. Цифровой измеритель длительности периода / М.К. Чмых, В.Г. Патюков. - Опубл. 15.07.78, Бюл. № 26.
18. Патюков В.Г., Чмых М.К. Квазиоптимальные оценки математических ожиданий случайных процессов // Известия Вузов. Приборостроение. - 1979. - № 1. - С. 7-12.
19. Патюков В.Г. Математическое моделирование погрешностей квантования при частотно-временных измерениях / Системные проблемы качества, математического моделирования и информационных технологий / Материалы международной научно-технической конференции и Российской научной школы. - М.: НИИ «Автоэлектроника», 2000. - С. 82-86.
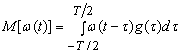 ,
(1)
,
(1)
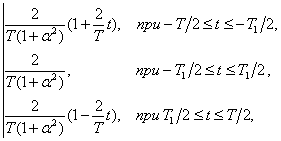


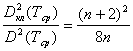 ,
,