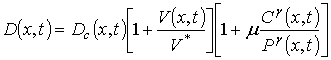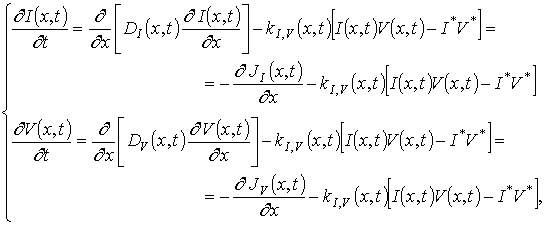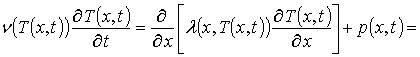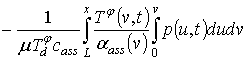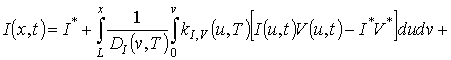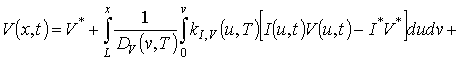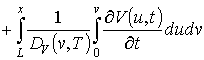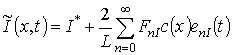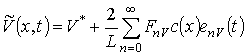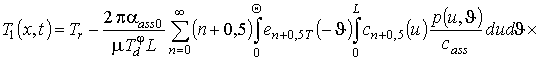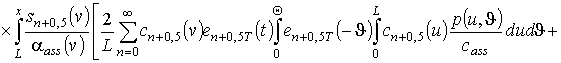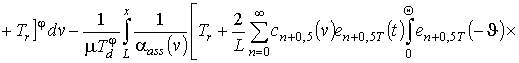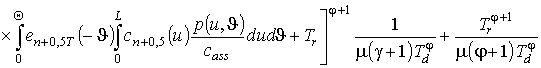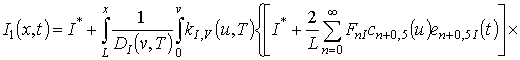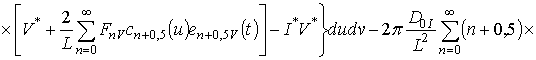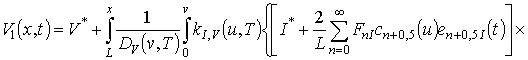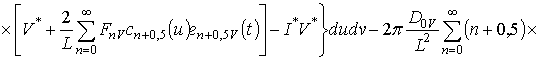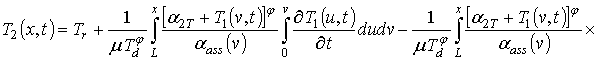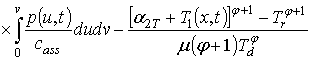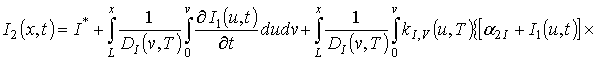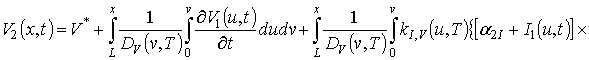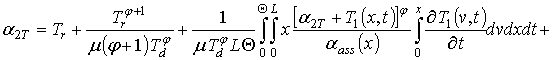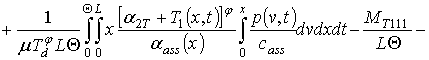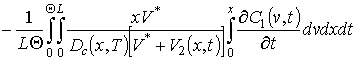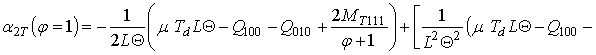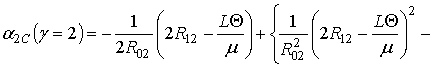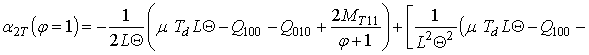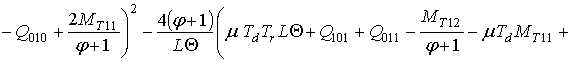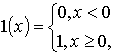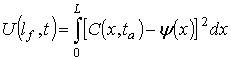Е.Л. Панкратов
Институт физики микроструктур
РАН,
Нижний Новгород
Получена 26 апреля 2007 г.
В настоящей работе проведен анализ динамики перераспределения имплантированной в многослойную структуру примеси с учетом температурной зависимости коэффициента диффузии в процессе отжига радиационных дефектов лазерными импульсами. Показано, что неоднородность твердотельной структуры позволяет увеличить резкость p-n-перехода, сформированного в результате имплантации, и равномерность распределения примеси в обогащенной ею области. Получены условия на пространственное распределение свойств имплантационно-легированной твердотельной структуры, при которых формируется более резкий p-n-переход с более равномерным распределением примеси в обогащенной ею области по сравнению с однородной структурой.
Введение
В настоящее время происходит интенсивное увеличение быстродействия устройств твердотельной электроники, а также – увеличение плотности элементов интегральных схем. Одним из направлений повышения быстродействия полупроводниковых устройств является уменьшение емкостей электронно-дырочных переходов [1,2]. Большой интерес для увеличения надежности полупроводниковых устройств представляет увеличение однородности распределения примеси в легированных областях и формирование более мелких p-n-переходов [1-3]. Актуальной задачей также является повышение точности теоретического описания технологических процессов, что приводит к повышению их предсказуемости и, как следствие, позволяет повышать воспроизводимость характеристик твердотельных устройств.
Для получения одиночных p-n-переходов используются различные технологические методы (см., например, [1-5]). Один из основных - внедрение примеси в исходную пластину или эпитаксиальный слой (ЭС) путем ее диффузии, имплантации или роста. В настоящей работе в развитие [6,7] рассматривается следующая многослойная структура, состоящие из ЭС толщины
(
) с коэффициентом диффузии
, осажденного на подложку толщины
(
) с коэффициентом диффузии
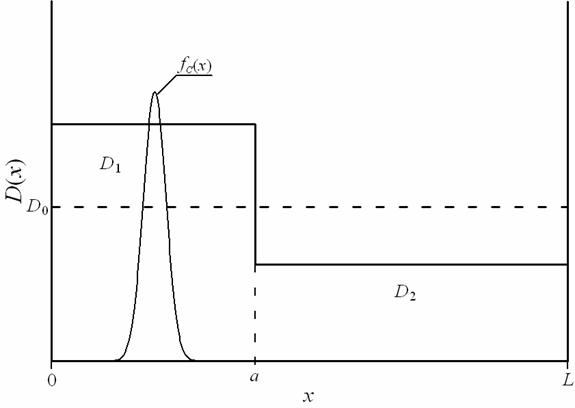
и заданным типом проводимости (p или n) (см. рис. 1). В ЭС формируется введенное с помощью имплантации распределение примеси, позволяющей создать в рассматриваемом слое необходимый тип проводимости (n или p). В момент времени
начинается отжиг радиационных дефектов длительностью
, приводящий с одной стороны к уменьшению количества дефектов и активизации примеси, с другой стороны - к уширению исходного распределения примеси и, как следствие, к отклонению характеристик формируемых диодов от запланированных при их проектировании значений. Целью данной работы является поиск условий, при которых распределение концентрации внедряемой примеси будет наиболее равномерным в ЭС, а в подложке количество внедряемой примеси будет практически отсутствовать.
При разгонке дефектов представляет интерес импульсный лазерный отжиг. Сильные стороны таких обработок заключаются в возможности модифицировать поверхностные слои без изменения свойств объема; нагревать локальные участки поверхности, что представляет интерес при производстве микросхем; и т.д. [8]. Несмотря на заметный интерес к лазерному отжигу в настоящее время существует небольшое количество работ, посвященных моделированию процессов массо- и теплопереноса при лазерном отжиге (см., например, [8-10]). По этой причине сопутствующей целью настоящей работы является поиск возможностей развития методики анализа данных процессов.
Метод решения
Динамика перераспределения примеси в процессе ее отжига в структуре
Рис. 1. Двухслойная структура (ДС) ЭС-подложка
ЭС-подложка может быть описана вторым законом Фика в следующей форме [1-3,5-7]
где
– пространственно-временное распределение примеси,
– пространственно-временное распределение потока примеси,
– коэффициент диффузии, величина которого зависит не только от динамических свойств примеси в материалах слоев ДС до имплантации примеси, а также от скорости прогрева и охлаждения ДС, а также от пространственно-временного распределения образовавшихся в процессе имплантации радиационных дефектов и концентрации примеси. Такие зависимости могут быть аппроксимированы следующими функциями [11,12] и [3]
где
– коэффициент диффузии примеси до начала имплантации при низком уровне легирования,
– концентрация вакансий,
– равновесное распределение вакансий,
– предел растворимости примеси, параметр
зависит от свойств материалов ДС и может принимать значения в интервале
[3]. Далее рассмотрим предельный случай, когда количество различных комплексов (например, дефектов) мало по сравнению количеством точечных дефектов и примеси. Пространственно-временное распределение концентрации точечных дефектов в данном случае может быть определено с помощью следующей системы уравнений [13]
где
и
- соответственно пространственно-временное распределение и равновесная концентрации междоузельных атомов;
и
– коэффициенты диффузии соответственно вакансий и междоузельных атомов;
– параметр рекомбинации [13];
– концентрация атомов решетки;
– энергия активации рекомбинации;
– радиус захвата при рекомбинации вакансий и междоузельных атомов;
- объем элементарной ячейки;
и
- пространственно-временные распределения потоков соответственно вакансий и междоузельных атомов. Динамика температурного поля, определяющего величины коэффициентов диффузии, удовлетворяет второму закону Фурье
, (4)
где
– теплоемкость легируемой структуры, которая может быть аппроксимирована следующим соотношением:
(см., например, [14]), а в представляющем наибольший интерес интервале температур экспоненциальной зависимостью от температуры можно пренебречь по сравнению с единицей, т.е.
;
– температура Дебая [13];
- коэффициент теплопроводности, температурная зависимость которого в представляющей интерес области может быть аппроксимирована следующим полиномом:
;
– объемная плотность мощности, пропорциональная мощности лазерного импульса
с длительностью
и площадью
, пространственно-временная зависимость которого может быть аппроксимирована следующим образом:
,
. Близкая по форме временная зависимость мощности приведена в [10]. Однако, приведенная в данной работе аппроксимация позволяет упростить анализ массо- и теплопереноса.
Уравнения (1), (3) и (4) необходимо дополнить граничными и начальными условиями
,
,
,
, (5)
,
,
.
Равновесные значения концентраций дефектов и температуры (совпадающее в данном случае с комнатной
), а также нулевое значение концентрации примеси на границе
могут быть использованы как упрощающие в данном случае решение краевых задач, т.к. ни примесь, ни дефекты фактически не достигают рассматриваемой границы ДС.
Для решения поставленной во введении цели поставим в соответствие уравнениям (1), (3) и (4) следующие интегро-дифференциальные уравнения
(6)
,
где
,
– температуропроводность ДС.
Для нахождения аналитического решения уравнений (6) и проведения с его помощью анализа динамики примеси и дефектов воспользуемся методом осреднения функциональных поправок [15]. В рамках этого метода для получения исходного приближения функции
,
,
и
, а также производные от этих функций заменяются на их средние значения a1 в правых частях уравнений (6), т.е.
,
,
и
и т.д. Далее полученные решения уточняются. Для ускорения сходимости метода осреднения функциональных поправок при определении исходного приближения в правых частях уравнений системы (6) заменим функции
,
,
и
на более точную их аппроксимацию. В качестве такой аппроксимации выберем решения уравнений диффузии и теплопроводности при усредненных коэффициентах диффузии и теплопроводности
и
, а также - нулевом параметре рекомбинации. В данном приближении функции
,
,
и
совпадают друг с другом
,
(7)
где
,
, l=I,V,C,
,
,
.
Подстановка (7) в (6) позволяет получить первое приближение по модифицированному в данной работе методу осреднения функциональных поправок в следующей форме
,
где
. Второе приближение концентраций примеси и дефектов, а также температуры определим с помощью стандартной процедуры [15], т.е. заменой функций
,
,
и
в правых частях уравнений (6) на следующие суммы:
,
,
и
, что позволяет получить
.
Параметры
,
,
и
определяются с помощью следующих соотношений [15]
где
,
. В окончательной форме соотношения для параметров
,
,
и
имеют вид
,
,
где
,

. Значения параметров
и
для некоторых значений
и
приведены ниже
,
,
,
,
,
,
,
,
,
где
,
,
,
,
,
,
,
,
,
,
,
,
.
Для выявлений основных зависимостей динамики перераспределения примеси от различных параметров обычно достаточно второго приближения решения уравнений (6). Полученные аналитические соотношения позволяют провести наглядное исследование динамики перераспределения примеси в течение отжига дефектов. Использование численных методов позволяет уточнить полученные результаты. По этой причине в дополнение к аналитическим использовались также и численные методы анализа процессов массо- и теплопереноса.
Результаты анализа
С помощью полученных в предыдущем разделе соотношений проведем анализ динамики перераспределения примеси в ДС. В данном случае пространственная зависимость коэффициентов диффузии и температуропроводности
и
может быть аппроксимирована с помощью следующих соотношений
,
,
где
,
,
и
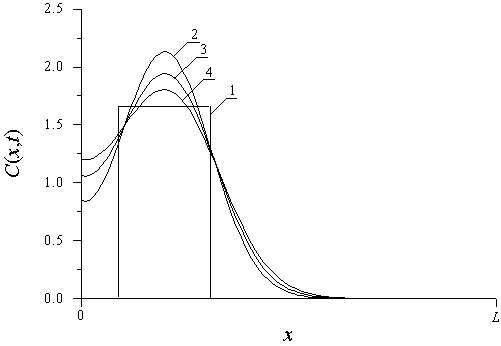
– значения коэффициентов диффузии и теплопроводности соответственно в ЭС и подложке. На рис. 2 приведено пространственное распределение имплантированной в ДС примеси после отжига длительностью Q в сравнении с аналогичным распределением в однородном материале. Для упрощения сравнения введена нормировка количества примеси:
. Из данного рисунка следует, что разница в значениях между коэффициентами диффузии слоев ДС приводит к увеличению равномерности распределения имплантированной примеси в обогащенной ею области. Одновременно с увеличением равномерности увеличивается и скорость снижения концентрации примеси вне обогащенной ею области, если граница обогащенной области находится в окрестности границы раздела между слоями ДС. Первый из этих эффектов позволяет уменьшить величину локальных разогревов полученной структуры при фиксированных размерах p-n-переходов или сформировать данный переход более приповерхностным при фиксированном допуске на разогрев структуры. Второй эффект позволяет снизить диффузионную емкость p-n-перехода. Может быть также показано, что при локальном отжиге может быть достигнуто меньшее уширение распределения примеси по сравнению с объемным отжигом.
Рис.2. Пространственное распределение имплантированной примеси после отжига длительностью
(кривые 1, 3) и
(кривые 2, 4). Кривые 1 и 2 – распределения примеси в однородном материале; кривые 3 и 4 – распределения примеси в ДС при
и
. Граница раздела между слоями имеет координату
Форма распределения примеси зависит от длительности отжига. При малой длительности отжига в легированных с помощью имплантации структурах сохраняется большое количество радиационных дефектов, что может ухудшить электрофизические свойства рассмотренных материалов [8,11,12]. Большая длительность отжига приводит к значительному уширению распределения примеси, что также не приводит к улучшению свойств получаемых с помощью имплантации диодных и транзисторных структур [1-3]. В асимптотическом случае, когда за время отжига радиационных дефектов распределение примеси уширяется мало, целесообразно проводить дополнительный отжиг примеси, позволяющий сместить p-n-переход к границе раздела между слоями ДС. Такое смещение позволяет увеличить равномерность распределения примеси в обогащенной ею области и резкость p-n-переходов за счет полуотражающего свойства границ раздела между слоями ДС. Проведем оценку такой длительности отжига, при которой достигается компромисс между увеличением равномерности распределения примеси в обогащенной ею области и увеличением градиента концентрации примеси в окрестности границ раздела между слоями ДС. Для оценки компромиссной длительности отжига воспользуемся введенным в [6,7] критерием, использованным для аналогичной длительности при формировании диффузионного p-n-перехода. В рамках такого критерия пространственно-временное распределение концентрации примеси
аппроксимируется идеализированным профилем примеси с концентрацией
и шириной обогащенной области
:
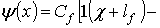
, где
,
– единичная функция, определяемая как
– координата максимума распределения примеси. Далее компромиссное время отжига
определяется из условия минимума среднеквадратической ошибки между реальным распределением примеси
и его аппроксимирующей функцией
Такой критерий проиллюстрирован с помощью рис. 3.
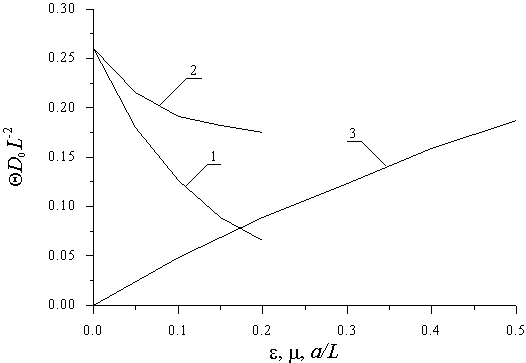
Полученные из условия минимума функционала (11) аппроксимации оптимальной длительности отжига приведены на рис. 4. Из последнего рисунка следует, что увеличение толщины ЭС приводит к увеличению компромиссного времени отжига. Увеличение параметров
и
позволяет
Рис. 3. Кривая 1 – идеализированное распределение примеси
; кривые 2-4 – реальные распределения примеси в различные моменты времени, растущие с номером кривых
Рис. 4. Зависимость безразмерного компромиссного времени отжига
, полученного из условия минимума функционала (11), от различных параметров ДС. Кривые 1 и 2 – зависимости
соответственно от
и
при нулевых значениях остальных двух параметров и
. Кривая 3 – зависимость
от
при
уменьшить время
, где параметр
введен следующим образом:
, 0£e <1, |h(x,t)|£1.
Заключение
Проведен анализ динамики перераспределения примеси, имплантированной в многослойную структуру, в процессе импульсного отжига. Выполненный анализ показал, что скачок коэффициента диффузии на границе раздела между слоями многослойной структуры позволяет изготовить более резкие p-n-переходы и увеличить однородность распределения концентрации легирующей примеси в обогащенной области. На основе введенных ранее критериев проведена количественная оценка длительности отжига, при котором достигается компромисс между увеличением равномерности распределения концентрации примеси в требуемой области структуры и увеличением резкости p-n-перехода. Также проведено исследование влияния изменения разницы между коэффициентами диффузии слоев многослойной структуры и их толщинами на величину компромиссного времени отжига.
Литература
[1] В.Г. Гусев, Ю.М. Гусев. Электроника. М.: Высшая школа, 1991. 622с.
[2] A.B. Grebene. Bipolar and MOS analogous integrated circuit design. New York, John Wyley and Sons, 1983, 894 p.
[3] З.Ю. Готра. Технология микроэлектронных устройств. - М.: Радио и связь. 1991. 528с.
[4] С.Т. Шишияну, Т.С. Шишияну, С.К. Райлян // ФТП. 2002. Т.36. № 5. С. 611-617.
[5] Ahlgren T., Likonen J., Slotte J., J. R
is
nen, M. Rajatore, J. Keinonen // Phys. Rev B. 1997. V.56, №8. P. 4597-4603.
[6] E.L. Pankratov // Phys. Rev. B. 2005. V.72, №7. P. 075201-075208.
[7] E.L. Pankratov, B. Spagnolo. // European Physical Journal B. - 2005. - V.46, №1. - P. 15-19.
[8] А.В. Двуреченский, Г.А. Качурин, Е.В. Нидаев, Л.С.Смирнов. Импульс-ный отжиг полупроводниковых материалов. - М.: Наука. 1982. 208 с.
[9] A.F. Corballo Sanchez, G. Gonzalez de la Cruz, Yu.G. Gurevich, G.N. Logvinov // Phys. Rev. B. 1999. - V.59, №16. - P. 10630-10638.
[10]. В.И. Мажукин, В.В.Носов, U. Semmler // Математическое моделирование. - 2000. - Т.12. №2. - С. 75 -83.
[11] Е.И. Зорин, П.В. Павлов, Д.И. Тетельбаум. Ионное легирование полупроводников. – М.: Энергия.1975.130 с.
[12] H. Ryssel, I. Ruge. Ion implantation. – B.G. Teubner, Stuttgart. 1978. 360с.
[13] P.M. Fahey, P.B. Griffin, J.D. Plummer // Rev. Mod. Phys. 1989. V. 61. № 2. P. 289-388.
[14] К.В. Шалимова Физика полупроводников. - М.: Энергоатомиздат, 1985. – 391 с.
[15] Ю.Д. Соколов, Прикладная механика. 1955. Т.1, P. 23-35.