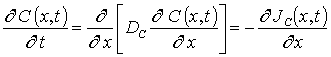Применение радиационной обработки материалов для уменьшения глубины залегания p-n-переходов в полупроводниковой гетероструктуре

Е. Л. Панкратов

Нижегородский архитектурно-строительный университет

Получена 13  мая 2011 г.

 

Аннотация. Ранее было показано, что формирование диффузионных и имплантационных p-n-переходов в полупроводниковых гетероструктурах и оптимизация отжига позволяет сформировать более мелкие p-n-переходы с более равномерным распределением примеси. В данной работе рассматривается возможность применения радиационной обработки материалов для одновременного усиления обоих эффектов.

Ключевые слова: увеличение резкости p-n-переходов; радиационная обработка материалов.

Abstract. Recently it has been elaborated an approach to decrease depth of diffusive- and implanted-junction rectifiers by manufacturing the rectifiers in a semiconductor heterostructure and optimization of annealing of dopant and radiation defects. At the same time with decreasing of depth of p-n-junction homogeneity of dopant distribution in doped area increases. In this paper we analyzed possibility to increase the both effects at one time by radiation processing of materials of the heterostructure.

Keywords: increasing of sharpness of a p-n-junctions; radiation processing of materials.

 

Введение

В настоящее время происходит интенсивное увеличение быстродействия устройств твердотельной электроники, а также увеличение степени интеграции элементов интегральных схем (ИС) [1-3]. Для увеличения быстродействия осуществляется поиск новых материалов с более высокими скоростями носителей заряда, разработка новых и усовершенствование уже разработанных технологических процессов [1-6]. Для увеличения степени интеграции элементов ИС также осуществляется разработка новых и усовершенствование уже разработанных технологических процессов [3,7]. В настоящее время для повышения как быстродействия, так и степени интеграции элементов ИС могут быть использованы различные модификации материалов, такие как радиационная модификация материалов или формирование пористости в них [8-10]. В данной работе рассматривается возможность применения радиационной модификации легируемого материала для уменьшения глубины залегания p-n-переходов.

 

Постановка задачи

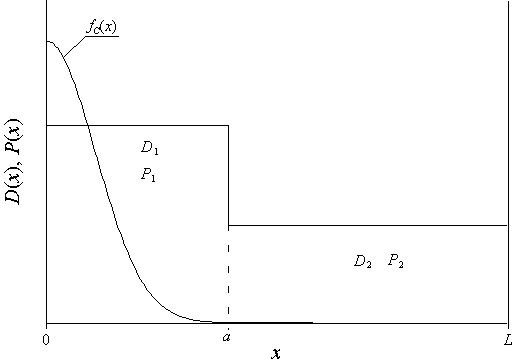
Для формирования p-n-переходов используются различные технологические методы. К ним относятся диффузионное легирование, ионная имплантация, эпитаксиальный рост [1-3]. Для уменьшения глубины их залегания, а также для увеличения степени интеграции элементов ИС могут быть использованы лазерный и микроволновый отжиги [11,12] и формирование дефектов легируемой структуры [13]. В работах [14-16] рассмотрен альтернативный метод уменьшения глубины залегания p-n-переходов, заключающийся в формировании двухслойной гетероструктуры (Г), состоящей из эпитаксиального слоя (ЭС) и подложки (П) (см. рис. 1). В ЭС вводится примесь. Далее проводится отжиг. В течении данного отжига примесь достигает границы раздела между слоями Г. В этом случае происходит формирование более компактного распределения примеси по сравнению с однородным материалом. Одновременно происходит увеличение равномерности распределения примеси также по сравнению с однородным материалом. Использование лазерного или микроволнового отжигов позволяет усилить одновременно оба эффекта за счет неоднородности температурного поля [17,18]. В данной работе анализируется влияние радиационной модификации ЭС также с целью усиления обоих эффектов.

 

Рис.1. Двухслойная гетероструктура, содержащая ЭС (xÎ[0,a]) и подложку (xÎ [a,L]). На данном рисунке также приведены начальное распределение примеси.

 

Методика анализа

Перераспределение примеси в рассматриваемой гетероструктуре определим путем решения второго закона Фика [1-3]

                           (1)

с граничными и начальными условиями

J_C (0,t) =J_C (L,t)=0, C (x,0)=f_C  (x).                                    (2)

В соотношениях (1) и (2) введены следующие обозначения: C(x,t) – пространственно-временные распределения концентрации примеси, J_С (x,t) – пространственно-временное распределение потока примеси, D_С – коэффициент диффузии примеси. Величина коэффициента диффузии определяется свойствами материалов в слоях Г, скорости прогрева и охлаждения Г (в соответствии с законов Аррениуса), а также пространственно-временными распределениями концентраций примесей и радиационных дефектов. Последние две зависимости коэффициента диффузии могут быть аппроксимированы следующим соотношением [2,19]

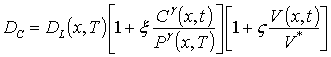.                                   (3)

В данном соотношении D_L (x,T) – пространственная (за счет многослойности Г) и температурная (по закону Аррениуса) зависимости коэффициент диффузии; T – температура отжига; P (x, T) – предел растворимости примеси; определяемый свойствами материала параметр g может принимать целые значения в интервале g Î[1,3] [2]; V (x,t) - пространственно-временное распределение концентрации радиационных вакансий; V^* - равновесное распределение вакансий. Концентрационная зависимость коэффициентов диффузии подробно обсуждается в [2]. Пространственно-временное распределение радиационных дефектов определялось с помощью следующей системы уравнений [20]

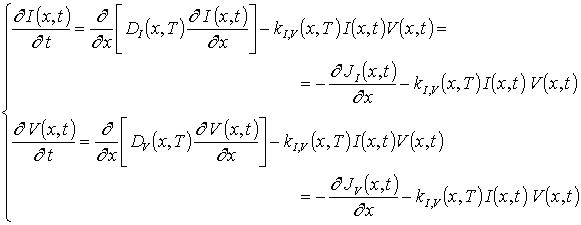 (4)

с граничными и начальными условиями

J_r (0,t)=J_r (L,t)=0, r (x,0)=f_r  (x), J_V (0,t)=J_V (L,t)=0.                     (5)

В системе уравнений (4) I(x,t) – пространственно-временное распределение концентрации междоузельных атомов; r =I,V; D_r(x,T) – коэффициенты диффузии междоузельных атомов и вакансий; k_I,V(x,T) – параметр рекомбинации дефектов.

Для определения пространственно-временного распределения радиационных дефектов преобразуем коэффициенты диффузии и параметр рекомбинации к следующему виду: D_r(x,T) =D_0r[1+e_r g_r(x,T)] и k_I,V(x,T)=k_0I,V[1+z h(x,T)], где D_0r и k_0I,V – средние значения соответствующих величин, 0£e_r <1, 0£z<1, | g_r(x,T)|£1, |h(x,T)|£1. Перейдем к следующим безразмерным переменным: , , ,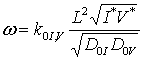. В новых переменных уравнения (4) принимают вид

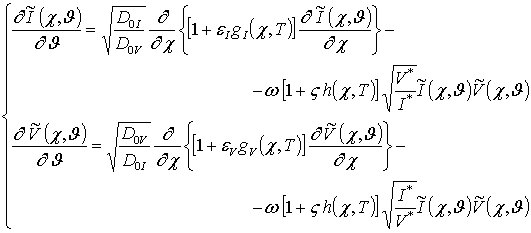       (6)

Решение уравнений (6) будем искать в виде степенных рядов

.                                  (7)

Подстановка данного ряда в уравнения (6) позволяет получить систему уравнений для исходных приближений концентраций дефектов , а также поправочных функций к ним  в следующем виде

 

;

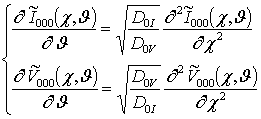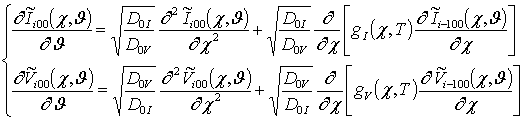, i ³1;

;

;

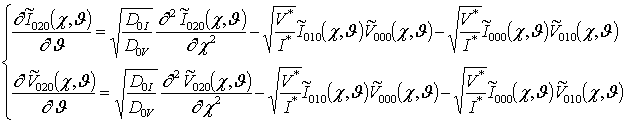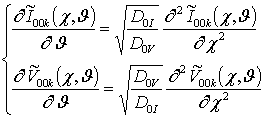;                                (8)

;

;

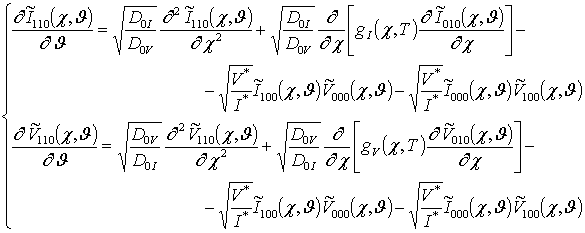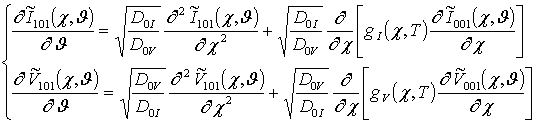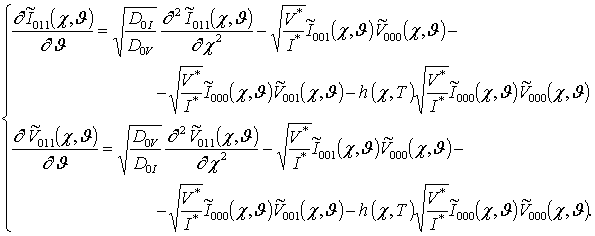
Подстановка рядов (7) в соответствующие граничные и начальные условия позволяет получить граничные и начальные условия для искомых функций

; ; .

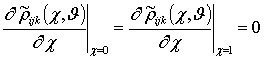Решениями уравнений (8) являются следующие функции

,

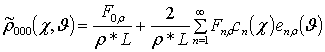где 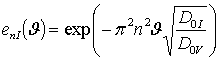 , , 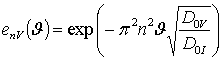c_n(c) = cos (p nc), ;

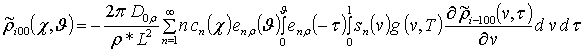, i ³1;

;

;

;

;

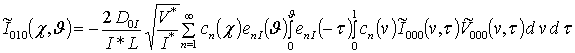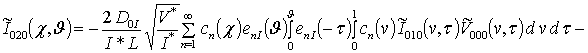
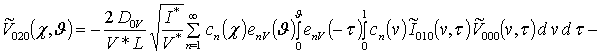
;                       (9)

,

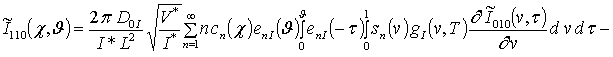
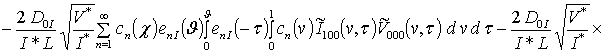
где s_n(c) = sin (p nc);

;

;

;

;

.

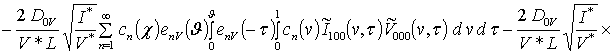
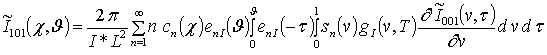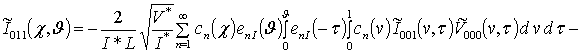
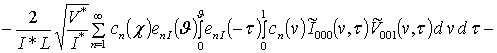
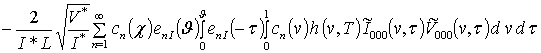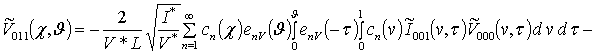
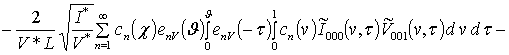
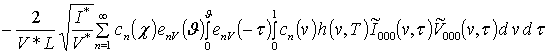Для качественного анализа перераспределения радиационных дефектов, а также для некоторых количественных оценок обычно достаточно второго приближения концентрации дефектов по параметрам, используемым в разложении (см., например, [14,15]). Аналитические результаты позволили выявить и наглядно проиллюстрировать основные зависимости. Для уточнения полученных результатов использовались численные методы.

Далее определим решение уравнения (1). Для этого представим коэффициент диффузии D_L (x,T) в виде суммы D_L(x,T) =D_0L[1+e _Lg_L(x,T)]. Решение уравнения (1) определим в виде следующего степенного ряда

.                                     (10)

Подстановка данного ряда в уравнение (1) позволяет получить следующую систему уравнений для исходного приближения концентрации примеси C₀₀(x,t), а также поправочных функций к ней C_ij(x,t) в следующем виде

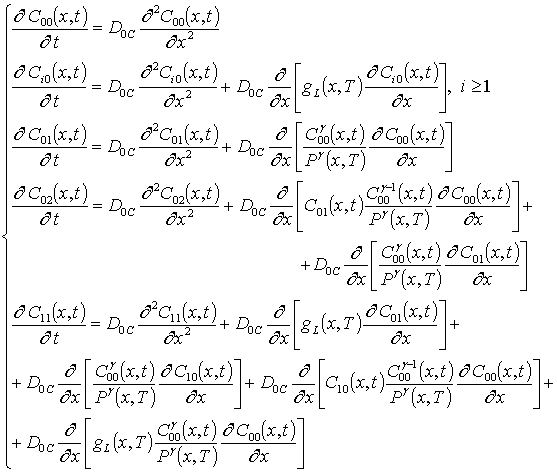 (11)

Подстановка ряда (10) в соответствующие граничные и начальные условия позволяет получить для искомых функций C_ij(x,t)

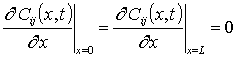; C₀₀(x,0)=f_C  (x); C_ij(x,0)=f_C  (x).

Решениями уравнений (11) являются следующие функции

,

где , e_nC(t) = exp(-p²n²D_0Lt/L²);

, i ³1;

;

;

.

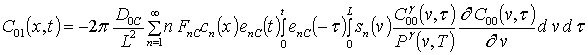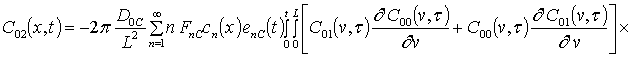
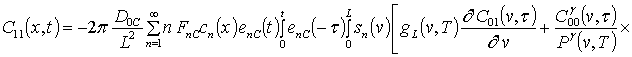
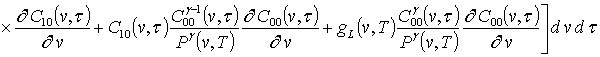Анализ пространственно-временного распределения концентрации примеси проводился аналитически во втором приближении по параметрам, используемым в соответствующем ряде, и уточнялся численно.

 

Результаты анализа

В данном разделе проведем анализ пространственно-временного распределения примеси в рассматриваемой Г (см. рис. 1). При этом будем считать, что ЭС прошел предварительную (перед введением примеси) радиационную обработку (потоком протонов или других частиц). В результате анализа было выявлено, что вне зависимости от наличия радиационных повреждений в Г наличие границы раздела между слоями Г позволяет одновременно увеличить резкость p-n-перехода и равномерность распределения примеси в обогащенной ею области. Следует заметить, что при малых длительностях отжига усиливается первый эффект, при больших длительностях отжига усиливается второй эффект. Наибольший компромисс между обоими эффектами достигается в случае, когда примесь по окончании отжига достигает границы раздела между слоями Г [14-18]. Это достижение может быть получено оптимизацией длительности отжига [14-18]. Проведение радиационных повреждений материала приводит к увеличению коэффициента диффузии примеси в нем. Этот результат моделирования качественно согласуется с рассмотренными в [9] экспериментальными данными. Распределения примеси в Г с радиационно модифицированным ЭС по сравнению с распределением примеси в Г с немодифицированным ЭС приведено на рис. 2. Данный рисунок показывает, что после радиационной модификации ЭС распределение примеси в нем становится более равномерным, а p-n-переход, сформированный в окрестности границы раздела между слоями Г, становится более резким по сравнению со случаем отсутствия модификации.

Рис. 2. Распределения примеси в двухслойной гетероструктуре. Кривые 1 – распределения примеси в гетероструктуре при условии, что коэффициент диффузии примеси в эпитаксиальном слое на 25% превышает коэффициент диффузии примеси в подложке. Кривые 2 – распределения примеси в гетероструктуре при условии, что коэффициент диффузии примеси в эпитаксиальном слое в 3 раза превышает коэффициент диффузии примеси в подложке. Сплошные кривые – исходная гетероструктура. Пунктирные кривые – гетероструктура с радиационно модифицированным эпитаксиальным слоем.

Заключение

В данной работе проведен анализ влияния радиационной модификации гетероструктуры эпитаксиальный слой – подложка на распределение введенной в нее примеси с целью формирования в рассматриваемой гетероструктуре p-n-перехода. Показано, что радиационная модификация эпитаксиального слоя позволяет усилить выявленный ранее [14-18] эффект одновременного увеличения резкости p-n-перехода и увеличения равномерности распределения примеси в обогащенной ею области в том случае, если p-n-переход сформирован в окрестности границы раздела между слоями гетероструктуры.

 

Данная работа поддержана грантом президента России (проект № МК-548.2010.2).

 

Литература

 

[1] A.B. Grebene. Bipolar and MOS analogous integrated circuit design. New York, John Wyley and Sons,1983,894p.

[2] З.Ю. Готра. Технология микроэлектронных устройств. - М.: Радио и связь. 1991. 528с.

[3] В.И. Лачин, Н.С. Савелов. Электроника. Ростов-на-Дону: Феникс, 2001. 446 с.

[4] С.Т. Шишияну, Т.С. Шишияну, С.К. Райлян. ФТП. 2002. Т.36 (5). С. 611-617.

[5] Ю.М. Покотило, А.Н. Петух, В.В. Литвинов, Письма в ЖТФ Т. 29 (19), С. 26-30 (2003).

[6] T. Ahlgren, J. Likonen, J. Slotte, J. Raisanen, M. Rajatore, J. Keinonen. Phys. Rev. B. 1997. V.56, (8). P. 4597-4603.

[7] Н.И. Волокобинская, И.Н. Комаров, Т.В. Матюхина, В.И. Решетников, А.А. Руш, И.В. Фалина, А.С. Ястребов. ФТП. 2001. Т.35 (8). С. 1013-1017.

[8] Н.А. Соболев. ФТП. 2010. Т.44 (1). С. 3-25.

[9] В.В. Козловский. Модифицирование полупроводников пучками протонов. Санкт-Петербург: “Наука”, 2003. 268 с.

[10] М.Г. Мынбаева, Е.Н. Мохов, А.А. Лаврентьев, К.Д. Мынбаев, Письма в ЖТФ. 2008. Т. 34 (17), С. 13-19.

[11] K.K. Ong, K.L. Pey, P.S. Lee, A.T.S. Wee, X.C. Wang, Y.F. Chong, Appl. Phys. Lett. 2006. 89 (17). 172111-172113.

[12] Ю.В. Быков, А.Г. Еремеев, Н.А. Жарова, И.В. Плотников, К.И. Рыбаков, М.Н. Дроздов, Ю.Н. Дроздов, В.Д. Скупов. Известия вузов. Радиофизика. 2003. Т.43, №3. С. 836-843.

[13] В.А. Козлов, В.В. Козловский. ФТП. 2001. Т.35 (7). С. 769-795.

[14] E.L. Pankratov. Phys. Rev. B. 2005. V.72 (7). P. 075201-075208.

[15] E.L. Pankratov, B. Spagnolo. The Eur. Phys. J. B. 2005. V. 46 (1). P. 15-19.

[16] E.L. Pankratov. Phys. Lett. A. 2008. Vol. 372 (11). P. 1897-1903.

[17] E.L. Pankratov. J. Appl. Phys. 2008. Vol. 103 (6). P. 064320-064330.

[18] E.L. Pankratov. Int. J. Nanoscience. 2008. Vol. 7 (4-5). P. 187–197.

[19] Е.И. Зорин, П.В. Павлов, Д.И. Тетельбаум. Ионное легирование полупроводников. М.: Энергия. 1975. 130 с.

[20] P.M. Fahey, P.B. Griffin, J.D. Plummer. Rev. Mod. Phys. 1989. V. 61. № 2. P. 289-388.