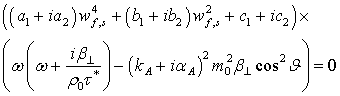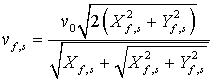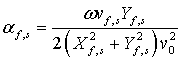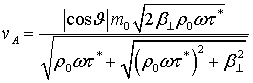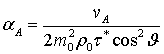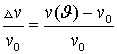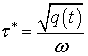УДК 53.098, 538.955
влияние релаксации магнитного поля на скорость звука в магнитной жидкости
И. Э. Овчинников
Московский государственный университет приборостроения и информатики
Получена 24 апреля 2013 г.
Аннотация. В линейном приближении рассмотрено распространение гидродинамических волн в магнитной жидкости с учетом процесса релаксации магнитного поля к своему равновесному значению. Получены выражения для фазовых скоростей и коэффициентов поглощения волны альфвеновского типа, быстрой и медленной магнитогидродинамических волн. Показано количественное соответствие расчетных значений и экспериментальных данных по анизотропии скорости ультразвука в магнитной жидкости на основе воды при длительном воздействии однородного постоянного магнитного поля.
Ключевые слова: магнитная жидкость, магнитное поле, ультразвук, наночастицы, магнетит.
Abstract: The propagation of hydrodynamic waves in magnetic fluid was considered in linear approximation with taking into account the process of relaxation of the magnetic field to its equilibrium value. The expressions for phase velocities and absorption coefficients were obtained for the Alfven type wave, the fast and slow magnetohydrodinamic waves. It was shown the calculated values to be in a quantitative agreement with experimental data on the ultrasonic velocity anisotropy in a water-based magnetic fluid under prolonged exposure of the homogeneous static magnetic field.
Key words: magnetic fluid, magnetic field, ultrasonics, nanoparticles, magnetite.
1. Введение
Настоящая статья является
развитием работы [1], где было рассмотрено распространение звука в магнитных
жидкостях параллельно внешнему однородному стационарному магнитному полю. Здесь
исследовано распространение звука в магнитной жидкости для всего диапазона
углов между волновым вектором и внешним однородным стационарным магнитным полем
согласно теоретическим положениям о релаксации
магнитного поля к своему равновесному значению [2,3]. В обзоре [3] были описаны
результаты многих работ по анизотропии скорости ультразвука, в том числе и экспериментов,
когда магнитная наножидкость выдерживалась от 10 до 200 часов в стационарном
однородном магнитном поле. За такие продолжительные времена успевала
сформироваться система цепевидных кластеров из магнитных наночастиц. В этих
случаях экспериментальные графики получились явно симметричными относительно точки 
. В работе [4] были получены
экспериментальные данные по анизотропии скорости ультразвука в магнитной
наножидкости на этапе формирования цепевидных кластеров из магнитных наночастиц,
т.е. от времени нахождения в стационарном однородном магнитном поле. В [4] экспериментальные
графики не являются достаточно симметричными относительно точки . В настоящей работе получены решения,
позволяют объяснить изменение анизотропии скорости ультразвука в магнитной
жидкости на основе воды от времени воздействия однородного постоянного магнитного
поля.
2. Распространение звука в магнитной жидкости
В статье [1] используется
система уравнений для макроскопического движения магнитной жидкости во внешнем
однородном постоянном магнитном поле из работ [2,3]. В настоящей статье в
декартовой системе координат внешнее магнитное поле направлено вдоль оси 
, а волновой вектор равен 
[5],
где 
– волновое число, а 
– коэффициент поглощения для
соответствующего типа волны, 
– мнимая единица.
Распространение звука в магнитной жидкости в линейном приближении проявляется
возмущениями плотности 
, компонент скорости 
и удельной намагниченности 
от своих равновесных значений. Возмущения
данных величин пропорциональны 
, что используется вместе с уравнениями
магнитостатики в линеаризованной системе (4) из статьи [1]. Далее получается система
уравнений в матричной форме [6]:
где 
–
вектор состояния, 
– круговая частота.
Ненулевые элементы матрицы 
перечислены ниже:
, 
, 
, 
, 
, 
,
, 
, 
,
, 
, 
,
,
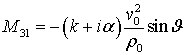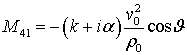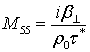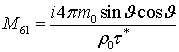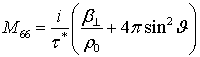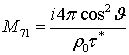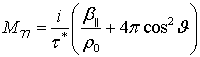где 
– равновесное
значение плотности магнитной жидкости; 
–
равновесное значение удельной намагниченности магнитной жидкости; 
– время релаксации
магнитного поля к своему равновесному значению; 
и 
– параметры магнитоупругости [3].
Из равенства нулю определителя матрицы (5), получается уравнение, которое является произведением двух дисперсионных уравнений:
где
, 
, 
,
, 
,
,
,
, 
.
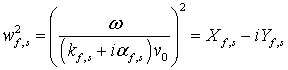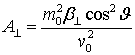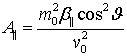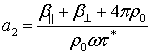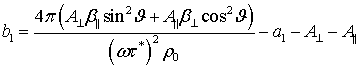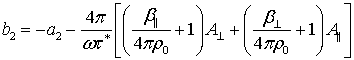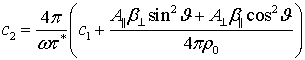Приравнивая к нулю первый
сомножитель в (2), получаем дисперсионное уравнение, которое определяет быструю
и медленную магнитогидродинамические волны с распространением возмущений 
,
,
,
и 
. Решениями данного дисперсионного
уравнения являются выражения для фазовых скоростей 
и коэффициентов поглощения данных
волн:
где
, 
,
, 
,
, 
.
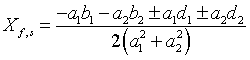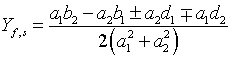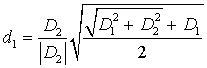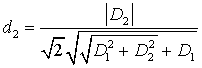Для фазовой скорости быстрой волны (3)
используется верхний знак в 
и 
, а ,соответственно, для медленной волны –
нижний знак. Так же для коэффициентов поглощения данных волн (4).
Если в (2) второй
сомножитель равен нулю, тогда получается дисперсионное уравнение, которое
определяет волну альфвеновского типа с распространением возмущений 
и 
. Решениями
данного дисперсионного уравнения являются фазовая скорость 
и коэффициент поглощения волны
альфвеновского типа:
При условиях 
,
из дисперсионного уравнения (2) следует,
что быстрая магнитогидродинамическая волна (3) распространяется с фазовой
скоростью:
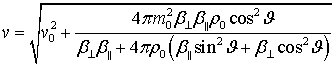, (7)
Скорость данной волны (7) совпадает со скоростью гидродинамической волны в идеальной магнитной жидкости с равновесной намагниченностью [7]. Коэффициент поглощения этой волны (4) стремится к нулю, что согласуется с результатами при распространении волн параллельно магнитному полю [1].
При условиях , волна
альфвеновского типа (5) и медленная магнитогидродинамическая волна (3) не
распространяются, т.к. фазовые скорости равны малым значениям 
, а коэффициенты поглощения (4,6)
становятся сравнимыми с волновыми числами данных волн 
.
Это согласуется с результатами для распространения волны альфвеновского типа
параллельно магнитному полю [1].
При 
,
в (3)
верен предел 
. Тогда для скоростей быстрой и медленной
волн получаются следующие выражения:
,
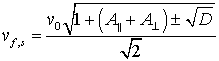(8)
где 
.
Выражения (8) совпадают со скоростями быстрой и медленной магнитозвуковых волн в идеальной магнитной жидкости с вмороженной намагниченностью [3] с учетом обозначений данной статьи. Коэффициенты поглощения данных волн (4) стремятся к нулю.
Скорость волны
альфвеновского типа (5) в пределе стремится к скорости
волны альфвеновского типа в идеальной магнитной жидкости с вмороженной
намагниченностью [3]:
.
В пределе коэффициент поглощения (6) этой волны
стремится к нулю. При угле есть особенность, но
фазовая скорость равна нулю, и данная волна не распространяется.
При использовании обозначений данной статьи для быстрой и медленной магнитогидродинамических волн получается следующее выражение для умноженного на длину волны коэффициента поглощения:
.
Из (6) следует, что для
волны альфвеновского типа скорость стремиться к нулю, а коэффициент поглощения
расходится, когда угол приближается к 
.
Однако, умноженный на длину волны коэффициент поглощения не зависит от угла:
.
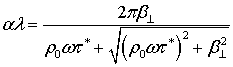3. Сравнение теоретических результатов с экспериментальными данными
В работе [4] использовалась магнитная
жидкость на основе воды W–40,
которая является магнитной наножидкостью, т.к. средний диаметр частиц магнетита
для W–40 равен 10 нм, а плотность равна 
г/см3. Образец магнитной
жидкости помещался в измерительную ячейку, которая медленно поворачивалась в
магнитном поле электромагнита. Расстояние между пьезопреобразователями ячейки
составляло 32 мм. Ячейка находилась при температуре 
C. Экспериментальные результаты [4]
представлены графическими зависимостями относительного изменения скорости
ультразвука от угла 
между волновым вектором и направлением
намагничивающего поля:
В соотношении (9) через 
обозначена скорость ультразвука в
магнитной жидкости при отсутствии внешнего магнитного поля. Угол варьировался в диапазоне 
.
Из работы [4] следует, что после 10
минут нахождения в однородном стационарном магнитном поле магнитная жидкость
медленно поворачивалась на 
в течение одного часа,
т. е. в сумме 70 минут в том же поле. Однако, анизотропия скорости ультразвука
была практически незаметна для значений индукции намагничивающего поля 100 мТ, 250
мТ, 400 мТ при частоте ультразвука 4 МГц. Анизотропия скорости ультразвука проявляется
после действия однородного стационарного магнитного поля в течение часа в другой
серии экспериментов.
В [4] наиболее интересным
является экспериментальный график для анизотропии ультразвука 4 МГц при 100 мТ.
В данном случае измерительная ячейка выдерживалась 1 час в однородном
стационарном магнитном поле при угле 
, а потом ее медленно
поворачивали с шагом 
. Далее, перед каждым измерением
проходила одна минута. Получается, что измерение скорости ультразвука при 
происходило через два часа после
нахождения магнитной жидкости в магнитном поле. В процессе эксперимента время
между 1 и 2 часами связано линейной зависимостью со значениями угла от до :
где 
мин.
Рис. 1. Зависимость относительного изменения аппроксимационной скорости распространения ультразвука в магнитной жидкости от времени
по формуле (11).
Магнитная наножидкость
является сложной системой, поэтому время релаксации магнитного поля к своему
равновесному значению может зависеть от многих параметров, и от условий
проведения эксперимента. В [4] ячейка с магнитной наножидкостью достаточно
медленно поворачивалась по отношению к внешнему однородному постоянному
магнитному полю, поэтому можно использовать зависимость времени релаксации от времени воздействия магнитного поля из
работы [1]. Предполагается, что если бы магнитное поле не поворачивалось, то
скорость ультразвука 
рис.1 имела бы от времени
полуэмпирическую зависимость [1]:
, (11)
где 
, 
, 
г/см3,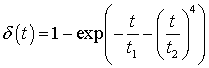 
, 
мин, 
мин.
Можно считать, что
выражение (11) определяет аппроксимационную скорость. Полуэмпирическая формула
для времени релаксации получена с использованием (11)
и работы [1]:
где
, 
, 
, 
.
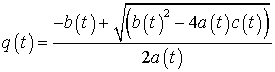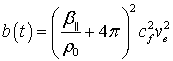
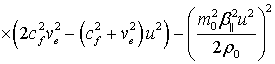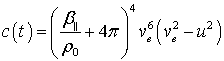Скорость распространения ультразвука
определяется формулой скорости для быстрой магнитозвуковой волны (3). Для
расчета скорости по уравнению (3) используются выражения (10-12). Значение
удельной намагниченности вычислялось как 
. Для значения индукции внешнего
магнитного поля 100 мТ величина намагниченности по формуле Ланжевена равна 
Гс [1]. Поскольку в работе [4] не было
приведено значение скорости ультразвука в отсутствие внешнего магнитного поля,
то для W–40 она предполагалась равной 
см/с.
Значения параметров г/см3, 
г/см3, 
мин были
определены из построения теоретической кривой по методу наименьших квадратов в
отношении экспериментальных данных (рис. 2). Экспериментальные значения
анизотропии скорости ультразвука около близки
к нулю, что согласуется с теоретическими результатами в модели магнитной
жидкости с вмороженной намагниченностью [3]. После одного часа () нахождения в магнитном поле анизотропия
скорости ультразвука 4 МГц была равна 0.3 %, а после двух часов () стала равна 0.501 %. Для определения
зависимости скорости от угла были решены прямая и обратная задачи, поэтому 
после одного часа () воздействия магнитного поля, и после двух часов ().
Это подтверждено численными расчетами. Из (12) получается, что время релаксации
с после одного часа () и 
с
после двух часов ().
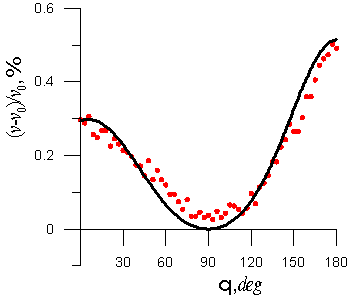
Рис. 2. Анизотропия скорости распространения ультразвука в магнитной жидкости: теоретическая кривая по формулам (3,9-12), точки – экспериментальные данные [4].
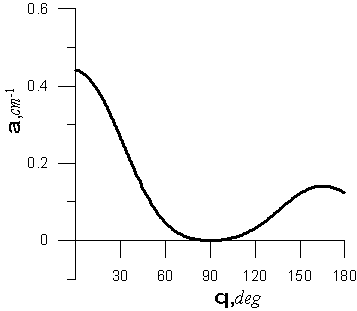
Рис. 3. Коэффициент поглощения ультразвука в магнитной жидкости по формулам (4,10-12).
Так же уравнения (4,10-12)
используются для расчета коэффициента поглощения при учете релаксации магнитного
поля к своему равновесному значению (рис 3). После одного часа нахождения в
магнитном поле () расчетный коэффициент
поглощения ультразвука 4 МГц был равен 0.466 см-1, а после двух
часов () он стал равен 0.136 см-1.
Получается, что с течением времени уменьшается вклад в поглощение ультразвука
от процесса релаксации магнитного поля с своему равновесному значению. Это
находится в согласии с результатами работы [1]. Расчетные значения
коэффициентов поглощения являются сравнимыми с известными экспериментальными
данными [3]. При угле расчетный
коэффициент поглощения равен нулю с хорошей точностью. Это очевидно из
дисперсионного уравнения (2): при распространяется
только одна волна со скоростью 
и без поглощения.
4. Выводы
В настоящей работе были объяснены результаты экспериментов по анизотропии скорости ультразвука в магнитной жидкости при помощи полуэмпирической зависимости для времени релаксации магнитного поля к своему равновесному значению. Данная зависимость была применена для анализа распространения звука в модели магнитной жидкости с вмороженной намагниченностью [1]. Получается, что при увеличении времени релаксации возрастает анизотропия скорости ультразвука в магнитной жидкости. Значит, время релаксации влияет на упругость среды. В данном случае, полученные численно коэффициенты поглощения ультразвука тоже проявляют анизотропию, которая уменьшается, когда увеличивается время релаксации магнитного поля к своему равновесному значению. Во многих работах [3] изменение скорости и коэффициента поглощения ультразвука в магнитной жидкости при длительном воздействии однородного постоянного магнитного поля связывают с образованием системы цепевидных кластеров, которая влияет на упругость среды. Данная система может формироваться даже в течение нескольких десятков часов, что зависит от типа магнитной жидкости и ее параметров. К настоящему времени, являются недостаточно определенными времена релаксации физических величин для различных используемых магнитных жидкостей. Данное исследование может быть полезным для метода измерения профиля скорости среды по доплеровскому сдвигу для ультразвука в магнитных средах [1].
[1] И.Э. Овчинников. Влияние постоянного магнитного поля на распространение ультразвука в магнитных жидкостях. // Журнал радиоэлектроники: электронный журнал. 2013. N1. URL: http://jre.cplire.ru/jre/jan13/12/text.pdf
[2] V.V. Sokolov, V.V. Tolmachev, “Propagation of shear waves in a magnetic liquid with frozen-in magnetization”, // Tech. Phys. Lett. 1997. Vol. 23, No. 1 p. 5-6.
[3] V.V. Sokolov, “Wave Propagation in Magnetic Nanofluids (A Reiew)”, // Acoustical Physics. 2010. Vol. 56. No. 6. pp. 972-988. DOI : 10.1134/S1063771010060229
[4] M. Motozawa, T. Sawada, “Ultrasonic Propagation in a Magnetic Fluid,” // Proceedings of the 3rd Int. Symp. on Ultrasonic Doppler Methods for Fluid Mechanics and Fluid Engineering EPFL (Switzerland, Lausanne, 2002) September 9-11, p. 137-142.
[5] L.D. Landau, E.M. Lifshitz, Electrodynamics of Continuous Media. New York: Pergamon, 1984.
[6] R.V. Polovin, V.P. Demutskii, Fundamentals of Magnetohydrodynamics, London, Plenum Publishing, 1990.
[7] I.E. Ovchinnikov, V.V. Sokolov, “Waves in Magnetic Fluids with Equilibrium and Frozen-In Magnetizations”, // Acoustical Physics, 2013. Vol. 59, No. 1, p. 51-55. DOI: 10.1134/S1063771012060115