УДК 004.93'11

ОБНАРУЖЕНИЕ РИТМОВ ГОЛОВНОГО МОЗГА ЧЕЛОВЕКА НА ОСНОВЕ КОРРЕЛЯЦИИ АНАЛИТИЧЕСКИХ СПЕКТРОВ ЭЭГ  В ОСНОВНЫХ ДИАПАЗОНАХ ЧАСТОТ

В. Е. Анциперов

Институт радиотехники и электроники им. В.А. Котельникова РАН

 

Статья получена 20 мая 2014 г.

Аннотация.  В работе представлены результаты развития методов многомасштабного корреляционного анализа применительно к задачам обнаружения и мониторинга ритмов коры головного мозга человека.  В частности, обсуждается усовершенствование техники вычисления частотно-временных представлений “конического” типа (являющихся частным случаем  корреляционных распределений) на основе недавно введенной нами концепции аналитических спектров. В отличие от классического спектрального анализа,  направленного на характеризующееся высоким разрешением оценивание индивидуальных частот, предлагаемые методы ориентированы в первую очередь на обнаружение и мониторинг колебательной активности нейронов в широких основных частотных диапазонах.

Ключевые слова: ЦОС, частотно−временной анализ ЭЭГ,  многомасштабный корреляционный анализ, аналитические спектры.

Abstract: Results of multiscale correlational analysis in application to EEG cortical rhythms detection improvements are presented and in detail discussed. In particular, the importance of frequency−temporal cone−shaped representations calculation techniques (which is the particular case of the correlation distributions) based on therecently introduced concept of the analytical spectra is in the center of discussion. Unlike classical spectral analysis, aimed at high resolution assessment of individual frequencies, the proposed methods are focused primarily on detection and monitoring of oscillatory neurons activity in the wide main frequency ranges.

Key words: DSP, time−frequency EEG analysis, multiscale correlational analysis, analytic spectra.

 

Введение

Электроэнцефалография (ЭЭГ) является одним из давно известных и широко применяемых методов динамического мониторинга активности головного мозга человека с разрешением по времени порядка нескольких миллисекунд (эквивалентная полоса частот ~ 100/500 Гц). Поскольку ЭЭГ сигналы снимаются с поверхности головы обследуемых (со скальпа), эта техника является неинвазивной (исключая случаи внутричерепного измерения у предоперационных пациентов) и поэтому широко рекомендована для нейроисследований, включая исследования ритмов коры головного мозга.

Хотя сигналы ЭЭГ представляют собой изменения электрических потенциалов на поверхности головы, индуцированы они совместной электрической активностью нейронов в коре головного мозга. Однако, ввиду наличия сопротивления нервных тканей, спинномозговой жидкости, черепной коробки и т.д. исходный сигнал нейронов оказывается существенно НЧ−отфильтрованным на скальпе. Кроме того, из-за случайной электрической активности мышц и кожи головы ЭЭГ сигнал оказывается еще и зашумленным. Таким образом, для извлечения физиологически значимых сведений о активности нейронных источников, включая их колебательную активность, необходимы робастные методы обработки сигналов ЭЭГ. Относительно недавно были предложены несколько новых подходов к оцениванию основных спектральных составляющих ЭЭГ сигнала и к описанию их динамики [1]. Однако, как подчеркивают специалисты, ни один из этих подходов не является универсальным, все имеет свои достоинства и недостатки. Поэтому задача поиска других подходов, методов, решений в области обнаружения и отслеживания ритмов головного мозга человека остается по-прежнему актуальной.

Нами ранее, в задачах об обнаружении в записях ЭЭГ эпилептиков характерных разрядов и оценивания их спектрального состава [2] и в проекте поиска частотно−временных маркеров в ЭЭГ пациентов−паркинсоников [3] был предложен свой, уникальный подход к анализу ЭЭГ сигналов на предмет поиска повторяющихся мотивов, событий. Этот подход назван нами многомасштабным корреляционным анализом и впервые был изложен в работе [4].

Многомасштабный корреляционный анализ (МКА) является несколько более широким подходом, чем традиционный спектральный анализ даже в его нестационарном варианте [5]. На основе МКА можно эффективно выделять участки квазипериодического поведения сигналов (соответственно сегментировать фрагменты с нарушением квазипериодичности), определять целый ряд связанных с квазипериодиченостью параметров и выявлять виды нарушения квазипериодичности в наблюдаемом сигнале. В каждом конкретном случае, на основе уточнения распределения корреляционного типа, можно ввести графическое многомасштабное представление сигналов на плоскости “время−смещение”. Данное представление является удобным, информативным и весьма эффективным средством для получения сведений о структуре сигнала “в целом”. Кроме того, в рамках МКА разработан и адаптирован к сигналам ЭЭГ ряд процедур оценивания характерных спектральных и временных масштабов.

В данной работе мы приводим результаты развития МКА применительно к задачам обнаружения и мониторинга ритмов коры головного мозга человека.  Эти результаты публикуются впервые, поскольку были получены буквально в последнее время. В частности, ниже мы обсуждаем усовершенствование техники вычисления частотно-временных представлений “конического” типа (являющихся частным случаем  корреляционных распределений) на основе недавно введенной нами концепции аналитических спектров [6,7]. Отметим, что предлагаемый нами подход ориентирован в первую очередь на обнаружение и мониторинг колебательной активности нейронов в широких частотных диапазонах, нежели на оценивание индивидуальных частот.

1. Основные частотные диапазоны колебательной активности нейронов мозга человека.

Спектры  ЭЭГ сигналов обычно демонстрируют максимумы (пики) спектральной мощности на различных частотах. Наиболее заметным из них является альфа-пик, который у здоровых взрослых людей обычно находится между 8 и 12 Гц. Этот пик был одним из первых обнаруженных в спектре  ЭЭГ человека, соответствующая частная активность доминирует в задних отделах коры головного мозга, блокируется при открывании глаз, связана со зрительными структурами мозга. Другие пики также были обнаружены в скором времени, включая бета-пики, занимающие, как правило, у здоровых взрослых людей диапазон 13-30 Гц, гамма пики на частотах выше 30 Гц, тета пики на 4-8 Гц, и острые пики на 11-15 Гц  (во сне). Последние пики характеризуются, как правило, четко определенной пространственной локализациуй.

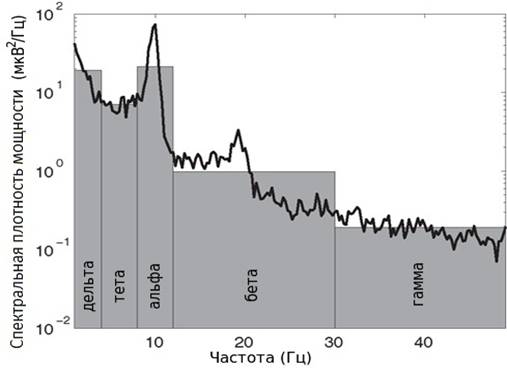
Рис. 1. Пример спектра ЭЭГ и диапазоны частот, соответствующие традиционной системе классификации ритмов. Общая мощность каждого ритма равна площади соответствующего прямоугольника (материал из Википедии — свободной энциклопедии, статья “Синхронизация (нейробиология)” )

 

Все перечисленные пики занимают широкий диапазон частот и частично перекрывают друг друга. Поэтому в типичных ЭЭГ записях спектр частот обычно принято подразделять на несколько диапазонов и соотносить частотный анализ с тем или иным из них. Каждому из  ЭЭГ диапазонов назначена соответствующая греческая буква δ, θ, α, β, γ и т.д. На Рис.1. изображена традиционная  символическая разметка спектра. Такой подход помогает аппроксимировать достаточно богатую структуру фактического ЭЭГ спектра посредством набора небольшого лишь нескольких параметров (см. Рис.1). Кроме того, индивидуальные спектральные пики у нормального взрослого человека оказываются, как правило, внутри зафиксированных границ стандартных диапазонов.

 

2. Билинейное, “конического” типа масштабно–частотно–временное представление сигналов на основе корреляции их аналитических спектров.  

Для обнаружения колебательной активности нейронов в соответствующих частотных диапазонах нами, в рамках многомасштабного корреляционного анализа [4], был развит новый подход к задачам обнаружения и мониторинга ритмов ЭЭГ. Основным средством для этого подхода стало упрощенное корреляционное распределение, которое, как оказалось, практически совпадает с частотно временным представлением (ЧВП) специального “конического” типа.

ЧВП “конического” типа – CKR (cone−shape kernel representations [8]), введены Дзао−Атласом−Марксом в 1990 году [9]. Носитель ядра CKR имеет вид двойного конуса в плоскости время–смещение |, что обеспечивает свойство “локальности” представления по отношению к поведению сигнала в окрестности .  Вид CKR в зависимости от формы ядра  [5] определяется формой:

 , (0)

 

где  и    – сигнал и его комплексное сопряжение,   − текущий момент времени,   − частота.  В наиболее частых для практики случаях  является действительной и симметричной функцией. В этом случае выражение (0) для CKR может быть преобразовано к следующему, свободному от модулей виду:

 .      (1)

 

Традиционно, роль оконной функции − формы ядра   состоит в адаптации ЧВП (1) к заданным классам сигналов с целью разрешения известного компромисса между размыванием спектральных компонент и просачиванием их в соседние временные области. Вместе с этим, анализ CKR, выполненный в [8] показал, что для подавления интерференционных членов, неизбежно присутствующих в квадратичных представлениях,  гораздо важнее  оказывается вид весовой функции , точнее форма и положение ее максимума, нежели форма самого ядра.  Именно, при отсутствии у  сингулярностей в  , максимум  оказываются смещенными от нуля на некоторое конечное расстояние , что наделяет CKR уникальными в классе квадратичных представлений свойствами фильтрации коротко− коррелированных (широкополосных) сигналов шумового вида.

В дальнейшем, для целей адаптации к частотным диапазонам, нам будет удобно рассматривать вместо заданной весовой функции  сразу целое их семейство, параметризованное, например, положениями их максимумов . В этом случае также и представление (1) будет зависимым от , т.е. оказывается масштабно–частотно–временным “спектром” вида:

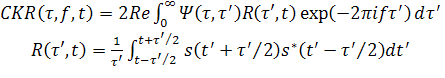  ,             (2)

 CKR в представлении (2) допускает очень простую интерпретацию. Именно, оно является оконным (финитным, с окном ) Фурье−преобразованием эрмитовой формы сигнала , которая, в свою очередь является (в стационарном случае) несмещенной и состоятельной оценкой корреляционной функции сигнала. Другими словами, по аналогии с теоремой Винера−Хинчина [5] CKR (2) в общем случае нестационарных процессов является дважды текущим – по  и по  – обобщенным спектром.

Оценки корреляционных функций  вида (2) ранее нами рассматривались и подробно анализировались [4] в качестве основного средства многомасштабного корреляционного анализа (МКА). В работе [10] также проведено сравнение cсвойств оценки (2) с традиционными оценками корреляционных функций. В частности, для стационарного случая было показано, что с увеличением масштаба (сдвига)  дисперсия оценки (2) монотонно уменьшается, в отличие от традиционного случая, где, начиная с некоторого сдвига, она возрастает.  Такая же особенность имеет место в многочисленных проведенных нами экспериментальных исследованиях с нестационарными сигналами.

Как нами было ранее показано [7], пределы интегрирования для  в выражении (2) можно распространить до , если ввести связанные с текущим моментом времени  локальное прошлое  и локальное будущее  сигнала :

 ,                                  (3)

где  – индикаторная функция положительной полуоси  – ступенька Хэвисайда. Очевидно, в зависимости от знака  нормированная свертка введенных посредством (3) функций есть:

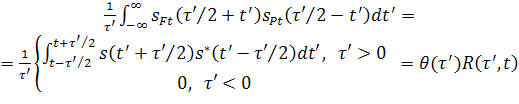         (4)

и при замене   в (2) сверткой (4) можно также распространить до  пределы интегрирования для CKR, произвольным образом доопределяя  на отрицательной полуоси  . Для определенности доопределим  нулем. В итоге получается, что CKR (2) есть Фурье−преобразование произведения функций, которое, как известно, есть свертка Фурье−преобразований сомножителей. Если в качестве сомножителей выбрать не    и  ,  а    и   , то, учитывая, что второй сомножитель будет теперь обычной сверткой, применяя теорему для Фурье−преобразования свертки, окончательно получим:

  ,             (5)

где семейство частотных окон  представляет собой множество  Фурье−образов семейства :

  ,                  (6)

а (комплексные) функции

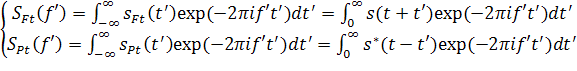     (7)

есть введенные в [6] аналитические спектры (локального прошлого и локального будущего) сигнала. В той же работе обсуждались многие замечательные свойства аналитических спектров, включая возможность их аналитического продолжения в нижнюю полуплоскость комплексного переменного и вытекающие из этой регулярности следствия. В данной работе, однако, наиболее важным достоинством аналитических спектров (7) является возможность упрощения с их помощью представления CKR (0,1) до очень компактного вида (5), обеспечивающего наиболее прозрачную интерпретацию.

 Действительно, для CKR (5) может быть записано следующее неравенство:

  ,          (8)

причем равенство достигается только когда  и   сопряжены друг другу (с некоторой фазовой коррекцией) на носителе окна , т.е. на некотором интервале с центром . Отсюда следует, что величина CKR при слабых изменениях спектра на частоте  при переходе через момент времени  практически равна энергии обычного спектра в полосе  . Наоборот, CKR обращается практически в ноль, если спектр в этой полосе исчезает слева или справа от  . Отсюда становится понятным известное достоинство CKR представлений, состоящее в их способности хорошо подчеркивать возникновение / исчезновение спектральных компонент (осуществлять временную сегментацию).

3. Масштабно–частотно–временное представление сигналов на основе аналитических спектров с семейством  весовых функций типа гамма-распределений.

Для того, чтобы перейти к вопросам практического использования представления (5), необходимо конкретизировать форму весовых функций семейства и, соответственно, семейство частотных окон  (6). Выберем в качестве семейства множество гамма–распределений, используя для начала традиционную параметризацию :

  ,                                  (9)

где –параметр, определяющий форму максимума , а – параметр, определяющий ее масштаб, в частности, положение максимума.  Отправляясь от явного вида весовых функций (9), несложно найти для них положения максимумов и их эффективную полуширину .  На основе этих соотношений можно в (9) перейти к новой параметризации и затем к нахождению семейства окон  (6), однако, удобнее перепараметризовать известный результат Фурье−преобразования гамма–распределений их характеристических функций:

  ,                  (10)

 где – квадрат “добротности” максимума. При высокой добротности выражение (10) для семейства частотных окон  может быть еще более упрощено до вида:

  .          (11)

Подставляя приближение (11) в точную формулу (5), получим окончательное выражение для масштабно–частотно–временного представления сигналов на основе аналитических спектров следующего вида:

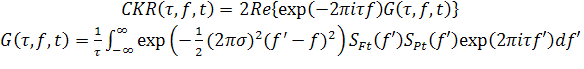 , (12)

представляющее основной результат изложенных выше рассмотрений.

Выводы

Основной вывод данной работы – найденное  CKR представление (12) является адекватным средством для решения задач обнаружения и мониторинга ритмов коры головного мозга человека. Техника вычисления частотно-временных представлений “конического” типа на основе концепции аналитических спектров [6,7] допускает простую реализацию и прозрачную интерпретацию результатов. Мы надеемся, что изложенный метод найдет многочисленные приложения и в других задачах исследования особенностей частотно-временных аспектов функционирования головного мозга человека.

 

Работа выполнена при финансовой поддержке РФФИ, грант N 16. 12-07-00104-а.

 

Литература

1.       S. Sanei, J. Chambers. EEG signal processing. // John Wiley & Sons, Inc., 2008 г.

2.       V. E. Antciperov, V. A. Morozov, and Y. V. Obukhov Representation of Epileptic Discharge Dynamics in EEGs on the Basis of Multiscale Correlative Signal Dynamics Analysis // “Pattern Recognition and Image Analysis”, Vol. 18, No. 2, 2008, pp. 342–346, ISSN 1054-6618.

3.       Обухов Ю.В., Анциперов В.Е. и др. Частотно-временной анализ электрической активности мозга при болезни Паркинсона // Нейродегенеративные заболевания. Фундаментальные и прикладные аспекты. Под ред. акад. М.В.Угрюмова. М: Наука, 2010, стр 112-129.

4.       Анциперов В.Е. Многомасштабный корреляционный анализ нестационарных, содержащих квазипериодические участки сигналов. // “Радиотехника и электроника”, 2008 г., т. 53, № 1, стр.73-85.

5.       Time-frequency analysis: concepts and methods. Edited by F. Hlawatsch and F. Auger. // GB and US: ISTE Ltd and John Wiley & Sons, Inc., 2008.

6.     Анциперов В.Е. Использование концепции аналитического спектра в вопросах интерпретации частотно-временных представлений сигналов. // Доклады VII Всероссийской научно-технической конференции «Радиолокация и радиосвязь», Изд. JRE - ИРЭ им. В.А.Котельникова РАН, Моcква, 2013 г., сс. 68-72.

7.       Анциперов В.Е. Использование аналитических спектров локального прошлого и будущего сигнала для формирования и анализа билинейных частотно-временных представлений // Доклады 16-й Международной Конференции “ Цифровая обработка сигналов и ее применение DSPA-2014”, т.1, ISSBN 978-5-905278-01-3, Москва, 2014, стр. 113-117.

8.     F. Hlawatsch, T. Manickam, R. Urbanke and B. Jones. Smoothed pseudo-Wigner distribution, Choi-Williams distribution, and cone-kernel representation: Ambiguity-domain analysis and experimental comparison. // Signal Processing, vol. 43, p. 149-168, 1995.

9.     Zhao Y., Atlas L. E., and Marks R. J. The use of cone-shape kernels for generalized time-frequency representations of nonstationary signals. // IEEE Trans. Acoustics, Speech, Signal Processing, V. 38, N 7, 1990, pp. 1084–1091.

10.         Анциперов В.Е. Новый метод оценки корреляционных функций в задачах обнаружения и обработки радиолокационных и связных сигналов // Доклады III Всероссийской конференции “Радиолокация и радиосвязь”, Москва, 26-30 октября 2009 г, стр. 887-881.