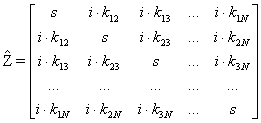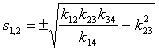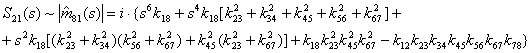ИССЛЕДОВАНИЕ КОМПЛЕКСНЫХ НУЛЕЙ ПЕРЕДАЧИ, ВОЗНИКАЮЩИХ ПРИ ВВЕДЕНИИ ДОПОЛНИТЕЛЬНЫХ
НЕКАСКАДНЫХ СВЯЗЕЙ МЕЖДУ РЕЗОНАТОРАМИ ФИЛЬТРА
Е. И. Лаврецкий
ОАО «МКБ Компас»
Статья получена 19 мая 2014 г.
Аннотация. В рамках эквивалентной схемы полосового фильтра в виде параллельных контуров, связанных между собой взаимными индуктивностями, проведено аналитическое исследование нулей передачи на комплексной плоскости, возникающих в результате введения дополнительных некаскадных связей между контурами. Рассмотрены физически симметричные структуры фильтров 4, 6, 8 и 10-го порядков. При анализе упор делался на нахождении таких связей, которые создавали ли бы нули передачи на действительной и мнимой осях комплексной плоскости. Установлено, что отрицательная связь между первым и последним резонаторами порождает одновременно пары нулей передачи на действительной и мнимой осях комплексной плоскости для структур 6-го и 10-го порядков. Для структур с 4-мя и 8-ю резонаторами положительные связи между первым и последним резонаторами производят нули только на действительной оси комплексной плоскости, а отрицательные – только на мнимой оси. Для экспериментального подтверждения выводов исследования был спроектирован и изготовлен гребенчатый фильтр 6-го порядка с центральной частотой 2642,5 МГц, в котором была введена дополнительная отрицательная связь между первым и последним резонаторами, реализована эллиптическая характеристика и уменьшены вариации группового времени задержки в полосе пропускания.
Ключевые слова: фильтр с несоседними связями, нули передачи, групповое время задержки.
Abstract: Within the scope of an equivalent lumped circuit of a bandpass filter in the form of synchronously tuned cavities coupled by mutual inductances, we analytically investigated transmission zeroes on the complex plane arising after introduction of some additional nonadjacent couplings between cavities. We considered physically symmetrical structures of filters with 4,6,8 and 10 cavities. In analysis we looked for the couplings producing transmission zeroes on the real and imaginary axes of the complex plane. It was established that a negative coupling between the first cavity and the last one simultaneously produces the pairs of transmission zeroes on the real and imaginary axes for the structures of the 6th and 10th orders. For the structures with 4 and 8 cavities the positive couplings between the first cavity and the last one produce zeroes only on the real axis of the complex plane, whereas the negative couplings produce zeroes only on the imaginary axis. To confirm experimentally the analytical results we designed and manufactured a cavity filter of 6th order of combline type with central frequency 2642.5 MHz. In this filter we obtained the elliptic transmission characteristic and the improved group delay time in the pass-band due to the introduction of an additional nonadjacent negative coupling between the first and last cavities.
Key words: a bandpass filter with nonadjacent couplings, transmission zeroes, group delay time.
1. Введение
Несоседние (некаскадные) связи резонаторов широко используются в современных полосовых фильтрах, чему посвящены многочисленные публикации, в частности [1-18]. Еще в пионерских работах [1-3] показана возможность благодаря введению несоседних связей создать нули коэффициента передачи и тем самым улучшить избирательность фильтра (получить фильтр с эллиптической характеристикой). Нули передачи, возникающие при наличии в фильтре параллельных ветвей распространения сигнала, для которых разность фаз коэффициентов передачи равна 180º, могут быть получены симметрично с обеих сторон полосы пропускания, только слева или справа от полосы пропускания и т.п. [4].
Другим основанием для введения дополнительных несоседних связей резонаторов является возможность уменьшить вариации группового времени задержки (ГВЗ) в полосе пропускания фильтра, т.е. возможность создания линейно-фазовых фильтров СВЧ. В работах [5-10] дано решение задачи реализации линейной фазовой характеристики, амплитудная характеристика реализуется без нулей передачи.
В дальнейших работах [11-14] рассматривалась задача получения в узкополосном фильтре как линейной фазовой характеристики, так и эллиптической характеристики. В [11] для решения этой проблемы предложено использовать для низкочастотного прототипа обобщенную форму чебышевской рациональной функции с заданным расположением нулей передачи на комплексной плоскости. В [12] представлен синтез фильтров с парой нулей передачи первого порядка на мнимой оси комплексной плоскости, улучшающих избирательность, или с парой нулей передачи на действительной оси комплексной плоскости, дающих изменение фазовой характеристики. В [13] предложена асимметричная реализация полосового фильтра для улучшения одновременно избирательности и линейности фазы и даны примеры реализации так называемых каскадных квадруплетных фильтров с четным числом резонаторов от 8 до 14. В частности, каскадный квадруплетный фильтр 8-го порядка имеет прототип с одной парой нулей передачи на мнимой оси комплексной плоскости для обеспечения избирательности, и с одной парой нулей на действительной оси комплексной плоскости для выравнивания ГВЗ. Строгий подход к проектированию полосовых фильтров с улучшенными ГВЗ и селективностью был представлен Пфитценмайером [14], который дал примеры разработки фильтров высокого порядка, имеющих 12 и 14 резонаторов. Он включил комплексные полюса в характеристическую функцию для создания дополнительных степеней свободы, позволяющих реализовать или эллиптическую характеристику или линеаризацию фазы. В статьях [15-18] даны другие интересные примеры синтеза фильтров с улучшенной избирательностью и линейностью фазы.
Подводя итог обзору литературы можно сделать вывод, что вопрос использования связей между несоседними резонаторами для получения нулей передачи (эллиптической характеристики) проработан достаточно глубоко. Для линейно-фазовых фильтров существует подход Роудса [5-10], приводящий к схеме фильтра, сложенного пополам, с дополнительными связями между резонаторами в половинках вверху и внизу. Частный случай схемы Роудса - это четверка резонаторов (квадруплет), в которой дополнительно связаны первый и четвертый резонаторы [12,13]. Другой подход для линейно-фазовых фильтров исходил от характеристической функции [14] и приводил к цепи высокого порядка (n=12 и 14), имеющей множество вариантов реализации, и для которой заранее неясно, какое минимальное количество некаскадных связей потребуется ввести и какие они будут - емкостные или индуктивные. Однако известно, что фильтры с несколькими некаскадными связями достаточно трудно настраивать, поэтому при практической реализации всегда целесообразно ограничиваться случаем одной или двух некаскадных связей. Отметим, что в большей части практических приложений не требуются фильтры с порядками более 8-го.
Целью данной статьи было проведение систематизации ряда топологических структур фильтров с дополнительными связями между резонаторами, порождающими комплексные нули передачи, и выработка приемов для выравнивания фазы в фильтрах с небольшим числом резонаторов. В отличие от классического метода теории фильтров, где сначала задается характеристическая функция, а затем находится топология фильтра, исследование исходило из топологии с заданным числом связей между резонаторами (топология порождала характеристическую функцию). В рамках эквивалентной схемы в данной статье проведено аналитическое исследование нулей передачи на комплексной плоскости, возникающих после введения несоседних связей между резонаторами фильтра. Рассмотрены физически симметричные структуры фильтров 4, 6, 8 и 10-го порядков, в которых введены связи между половинками фильтров. При анализе было найдено положение на комплексной плоскости нулей передачи для положительных и отрицательных дополнительных связей. Наиболее интересная ситуация для практики соответствует нулям передачи на мнимой оси комплексной плоскости (эллиптическая характеристика фильтра) и на действительной оси комплексной плоскости (изменение ГВЗ). Установлено, что отрицательная связь между первым и последним резонаторами порождает одновременно пары нулей передачи на действительной и мнимой осях комплексной плоскости для структур 6-го и 10-го порядков. Для структур с 4-мя и 8-ю резонаторами положительные связи между первым и последним резонаторами производят нули передачи только на действительной оси комплексной плоскости, а отрицательные – только на мнимой оси. В Приложении объяснено, почему нули коэффициента передачи прототипа на действительной оси комплексной плоскости приводят к уменьшению вариаций ГВЗ в полосе пропускания фильтра, создавая локальный экстремум (подъем) групповой задержки на центральной частоте фильтра.
Для практических приложений наиболее интересным оказывается случай введения отрицательной некаскадной связи между первым и последним резонаторами в фильтре 6-го порядка, на который, по сведениям автора статьи, до сего момента в литературе не обращалось внимания. Здесь единственная некаскадная связь может одновременно произвести две пары нулей передачи- пару нулей на мнимой оси и пару нулей на действительной оси комплексной плоскости, т.е. улучшить одновременно избирательность фильтра и линейность фазы. В некоторых ситуациях такой фильтр с только одной некаскадной связью может быть рассмотрен как оптимальное практическое техническое решение, в нем имеется минимальное усложнение схемы в сравнении с обычным чебышевским фильтром. Для экспериментальной проверки был спроектирован, изготовлен и протестирован гребенчатый фильтр 6-го порядка с отрицательной некаскадной связью между первым и шестым резонаторами. Результаты испытаний подтвердили вывод о возможности одновременно улучшить избирательность и линейность фазы, используя одну дополнительную некаскадную связь.
2. Анализ эквивалентной схемы полосового фильтра
Рассмотрим эквивалентную схему полосового фильтра в
виде ![]() синхронно настроенных параллельных контуров (резонаторов) с
индуктивностями
синхронно настроенных параллельных контуров (резонаторов) с
индуктивностями ![]() и емкостями
и емкостями ![]() , связанных между собой взаимными индуктивностями
, связанных между собой взаимными индуктивностями ![]() . Внешние связи с подводящими линиями
обеспечиваются идеальными трансформаторами с трансформацией 1:n1 и n2:1,
связанными с 1-м и N-м контурами, соответственно. Сопротивление нагрузки и
источника примем одинаковыми и равными
. Внешние связи с подводящими линиями
обеспечиваются идеальными трансформаторами с трансформацией 1:n1 и n2:1,
связанными с 1-м и N-м контурами, соответственно. Сопротивление нагрузки и
источника примем одинаковыми и равными ![]() . Данная эквивалентная схема широко
использовалась при проектировании узкополосных фильтров, например, в [2,3,13,16,17].
Рассмотрим полосовой фильтр с центральной круговой частотой
. Данная эквивалентная схема широко
использовалась при проектировании узкополосных фильтров, например, в [2,3,13,16,17].
Рассмотрим полосовой фильтр с центральной круговой частотой ![]() и полосой
и полосой ![]() . Выберем
. Выберем ![]() и
и ![]() , тогда N´N нормированная матрица сопротивлений для реактивной цепи с взаимно
- индуктивными связями имеет вид:
, тогда N´N нормированная матрица сопротивлений для реактивной цепи с взаимно
- индуктивными связями имеет вид:
где 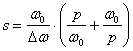 -
комплексная частота низкочастотного прототипа (арифметически равна сопротивлению
контура, деленному на
-
комплексная частота низкочастотного прототипа (арифметически равна сопротивлению
контура, деленному на ![]() ),
), ![]() - комплексная частота
полосового фильтра,
- комплексная частота
полосового фильтра, ![]() - нормированный импеданс связи для узкочастотной аппроксимации. Коэффициент
передачи между источником и нагрузкой в рассматриваемой цепи равен
- нормированный импеданс связи для узкочастотной аппроксимации. Коэффициент
передачи между источником и нагрузкой в рассматриваемой цепи равен
где ![]() - элемент нормированной матрицы
проводимостей, рассчитываемой как обратная матрица для матрицы сопротивлений
(1)
- элемент нормированной матрицы
проводимостей, рассчитываемой как обратная матрица для матрицы сопротивлений
(1) ![]() . Фильтры с дополнительными несоседними
связями имеют полином в числителе коэффициента передачи (2), который может быть
записан для аналитического исследования. Коэффициент передачи фильтра (2) пропорционален величине
. Фильтры с дополнительными несоседними
связями имеют полином в числителе коэффициента передачи (2), который может быть
записан для аналитического исследования. Коэффициент передачи фильтра (2) пропорционален величине
где ![]() есть минор для элемента
есть минор для элемента ![]() матрицы сопротивлений
матрицы сопротивлений ![]() (1) [19]. Таким образом, рассчитывая
указанные миноры, можно вычислить требуемый полином числителя и определить его
нули на комплексной плоскости.
(1) [19]. Таким образом, рассчитывая
указанные миноры, можно вычислить требуемый полином числителя и определить его
нули на комплексной плоскости.
В рамках данной эквивалентной схемы можно вводить дополнительные несоседние связи между резонаторами и фиксировать изменения амплитудной и фазовой характеристик фильтра, то есть к характеристической функции приходить от топологии фильтра (в отличие от классического метода теории фильтров, где сначала задается характеристическая функция, а затем находится топология фильтра). Целесообразно сначала синтезировать каскадную схему фильтра с чебышевской характеристикой, далее в цепь вводить дополнительные связи. Аналогичный подход был ранее использован Вензелем [11]. Расчеты показали, что подходящие несоседние связи, как правило, в 5-10 раз меньше по абсолютной величине каскадных связей, поэтому их введение не приводит к значительным изменениям в ширине полосы пропускания фильтра и пульсациях в полосе пропускания. Поэтому достаточно небольшой подстройки и оптимизации каскадных связей для достижения равнопульсирующих обратных потерь в полосе фильтра для финальной схемы с дополнительными связями.
3. Нули коэффициента передачи и групповая задержка в низко-частотном прототипе
В этом разделе определены положения нулей коэффициента передачи прототипа и рассчитаны групповая задержка прототипа по формуле (13). Анализ ограничен несколькими физически- симметричными структурами полосно-пропускающих фильтров четного порядка с электрически симметричными характеристиками. При анализе полагалось, что все каскадные связи положительны, в то время как некаскадные связи могут быть положительны или отрицательны. Положительные и отрицательные связи соответствуют соответственно положительным и отрицательным взаимным индуктивностям.
3.1. Фильтр с 4-мя резонаторами с ![]()
Коэффициент передачи фильтра
пропорционален минору ![]()
Нули для ![]() рассчитываются элементарным образом:
рассчитываются элементарным образом:
Формула (5) совпадает с формулой в статье [1]. Очевидно, что
при ![]() нули расположены на мнимой оси комплексной
нули расположены на мнимой оси комплексной ![]() - плоскости,
производя два нуля передачи на действительных частотах, в то время как при
- плоскости,
производя два нуля передачи на действительных частотах, в то время как при ![]() нули расположены на действительной оси
комплексной плоскости (при условии, что подкоренное выражение положительно).
Эти ситуации хорошо исследованы и разобраны в [12]. На рис. 1 показаны
групповая задержка и положение нулей для несоседних связей разных знаков.
нули расположены на действительной оси
комплексной плоскости (при условии, что подкоренное выражение положительно).
Эти ситуации хорошо исследованы и разобраны в [12]. На рис. 1 показаны
групповая задержка и положение нулей для несоседних связей разных знаков.
3.2. Фильтр с 6-ю резонаторами с ![]()
Коэффициент передачи фильтра
пропорционален минору ![]()
Нули ![]() находятся как решение биквадратного уравнения:
находятся как решение биквадратного уравнения:
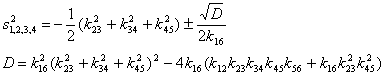 . (7)
. (7)

(а)
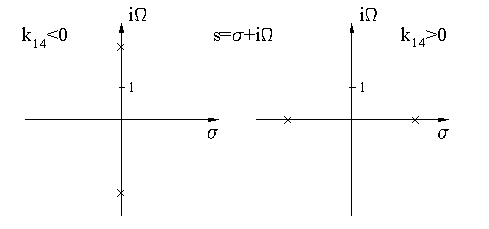
(б)
Рис. 1. Характеристики полосового
фильтра с 4-мя резонаторами с несоседней связью ![]() : (а) структурная схема и групповая
задержка, (б) нули коэффициента передачи
: (а) структурная схема и групповая
задержка, (б) нули коэффициента передачи
(а)
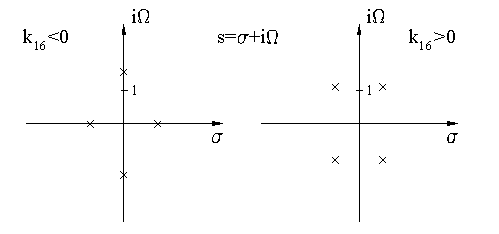
(б)
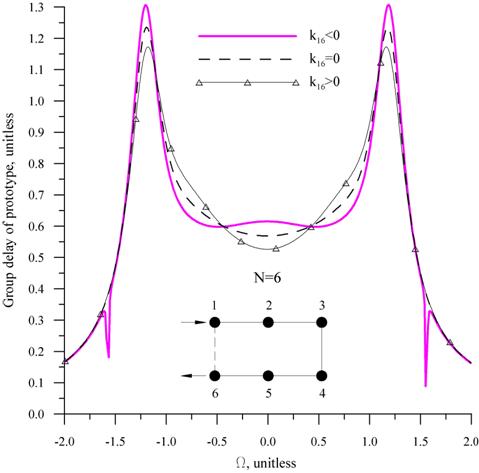
Рис. 2. Характеристики полосового
фильтра с 6-ю резонаторами с несоседней связью ![]() : (а) структурная схема и групповая задержка,
(б) нули коэффициента передачи
: (а) структурная схема и групповая задержка,
(б) нули коэффициента передачи
Имеем дискриминант ![]() для
для ![]() , тогда
, тогда ![]() есть действительные числа. Отсюда имеем
пару нулей
есть действительные числа. Отсюда имеем
пару нулей ![]() на мнимой оси комплексной
на мнимой оси комплексной ![]() -
плоскости, производящих нули передачи фильтра на действительных частотах, и
пару нулей
-
плоскости, производящих нули передачи фильтра на действительных частотах, и
пару нулей ![]() на действительной оси комплексной плоскости, изменяющих
групповую задержку. Для
на действительной оси комплексной плоскости, изменяющих
групповую задержку. Для ![]() (полагая, что несоседние связи значительно меньше
каскадных связей) имеем дискриминант
(полагая, что несоседние связи значительно меньше
каскадных связей) имеем дискриминант ![]() , поэтому квадраты нулей
, поэтому квадраты нулей 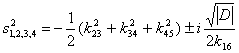 являются комплексными числами. В
этом случае четыре нуля формируют квадруплет на комплексной
являются комплексными числами. В
этом случае четыре нуля формируют квадруплет на комплексной ![]() - плоскости. На рис. 2 показаны групповая
задержка и расположение нулей для данного случая. Таким образом, отрицательная
связь
- плоскости. На рис. 2 показаны групповая
задержка и расположение нулей для данного случая. Таким образом, отрицательная
связь ![]() приводит к возникновению эллиптической характеристики фильтра
и локальному экстремуму ГВЗ на центральной частоте фильтра. Положительная связь
приводит к возникновению эллиптической характеристики фильтра
и локальному экстремуму ГВЗ на центральной частоте фильтра. Положительная связь
![]() не дает эллиптической характеристики, увеличивает вариации
ГВЗ в полосе фильтра.
не дает эллиптической характеристики, увеличивает вариации
ГВЗ в полосе фильтра.
3.3. Фильтр с 6-ю резонаторами с ![]() и
и ![]()
Коэффициент передачи фильтра
пропорционален минору ![]()
Сравнивая (8) и (6), делаем вывод, что введение ![]() только модифицирует два коэффициента
полинома. Степень полинома как в (6), так и в (8) определяется наличием связи
только модифицирует два коэффициента
полинома. Степень полинома как в (6), так и в (8) определяется наличием связи ![]() . Отсюда следует вывод, что
. Отсюда следует вывод, что ![]() есть дополнительный элемент
настройки для коэффициента передачи фильтра. С практической точки может
оказаться удобно вводить
есть дополнительный элемент
настройки для коэффициента передачи фильтра. С практической точки может
оказаться удобно вводить ![]() и
и ![]() . Связь
. Связь ![]() даст два нуля передачи на мнимой оси комплексной
плоскости и два нуля на действительной оси комплексной плоскости, как
рассмотрено в предыдущем подразделе. Связь
даст два нуля передачи на мнимой оси комплексной
плоскости и два нуля на действительной оси комплексной плоскости, как
рассмотрено в предыдущем подразделе. Связь ![]() может быть введена для подстройки
положения указанных нулей. Такая структура с двумя несоседними связями
использовалась для проектирования фильтра с коаксиальными резонаторами в [15].
может быть введена для подстройки
положения указанных нулей. Такая структура с двумя несоседними связями
использовалась для проектирования фильтра с коаксиальными резонаторами в [15].
3.4. Фильтр с 8-ю резонаторами с ![]()
Коэффициент передачи фильтра
пропорционален минору ![]()
Нули ![]() могут быть рассчитаны с помощью формул Кардано как корни кубического
полиномиального уравнения или численно. Для сохранения места аналитические выражения
для нулей не приводим. Анализ нулей показывает, что для
могут быть рассчитаны с помощью формул Кардано как корни кубического
полиномиального уравнения или численно. Для сохранения места аналитические выражения
для нулей не приводим. Анализ нулей показывает, что для ![]() имеется пара нулей на мнимой оси и
квадруплет комплексных нулей (вне осей). Для
имеется пара нулей на мнимой оси и
квадруплет комплексных нулей (вне осей). Для ![]() имеется пара нулей на действительной
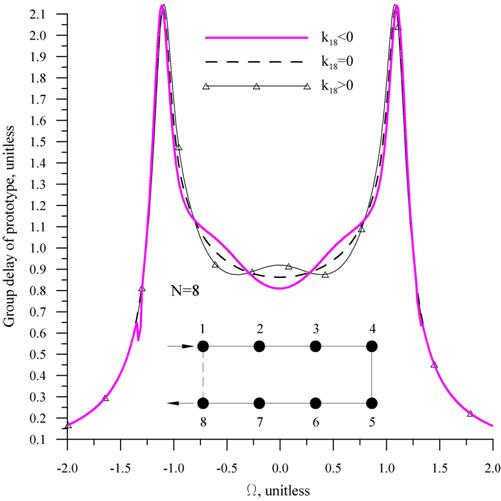
оси и также квадруплет комплексных нулей. На рис. 3 демонстрируется групповая
задержка и положение нулей для связей разных знаков.
имеется пара нулей на действительной
оси и также квадруплет комплексных нулей. На рис. 3 демонстрируется групповая
задержка и положение нулей для связей разных знаков.
3.5. Фильтр с 8-ю резонаторами с ![]() и
и ![]()
Коэффициент передачи фильтра
пропорционален минору ![]()
Возникающий фильтр называется каскадно-квадруплетным, для
него коэффициент передачи пропорционален произведению двух скобок,
соответствующих цепям 4-го порядка. В зависимости от знака несоседней связи
каждая скобка может дать или пару нулей на действительной оси комплексной ![]() - плоскости или пару нулей на мнимой оси
комплексной плоскости. Знаки несоседних связей могут быть выбраны независимо.
Этот случай хорошо исследован в [13].
- плоскости или пару нулей на мнимой оси
комплексной плоскости. Знаки несоседних связей могут быть выбраны независимо.
Этот случай хорошо исследован в [13].
(а)

(б)
Рис. 3. Характеристики полосового
фильтра с 8-ю резонаторами с несоседней связью ![]() : (а) структурная схема и групповая
задержка, (б) нули коэффициента передачи
: (а) структурная схема и групповая
задержка, (б) нули коэффициента передачи
3.6. Фильтр с 10-ю резонаторами с ![]()
Коэффициент передачи фильтра пропорционален минору ![]() , который является полиномом 8-го
порядка. Аналитическое выражение для этого полинома слишком громоздко, поэтому
приводятся только графические данные. Нули
, который является полиномом 8-го
порядка. Аналитическое выражение для этого полинома слишком громоздко, поэтому
приводятся только графические данные. Нули ![]() были рассчитаны численно. Для
были рассчитаны численно. Для ![]() имеются пары нулей на действительной
и мнимой осях комплексной плоскости и квадруплет комплексных нулей. Наоборот,
для
имеются пары нулей на действительной
и мнимой осях комплексной плоскости и квадруплет комплексных нулей. Наоборот,
для ![]() имеются два квадруплета комплексных нулей. На рис. 4
показаны групповая задержка и положение нулей для различных знаков связей.
имеются два квадруплета комплексных нулей. На рис. 4
показаны групповая задержка и положение нулей для различных знаков связей.
Таким образом, отрицательная связь между первым и последним резонаторами порождает пары нулей передачи на действительной и мнимой осях комплексной плоскости для структур 6-го и 10-го порядка (следующая структура более высокого порядка с аналогичными свойствами имеет 14 резонаторов). Наоборот, чтобы произвести нули на действительной оси комплексной плоскости для структур с 4-мя и 8-ю резонаторами требуются положительные несоседние связи, а на мнимой оси комплексной плоскости- отрицательные несоседние связи. Влияние нулей коэффициента передачи прототипа на действительной оси комплексной плоскости на ГВЗ поясняется в Приложении.

(а)
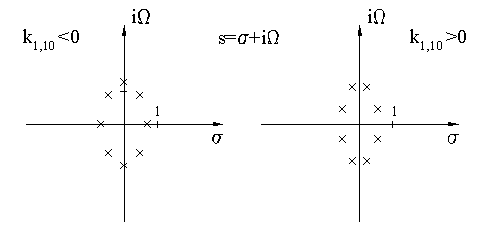
(б)
Рис. 4. Характеристики полосового
фильтра с 10-ю резонаторами с несоседней связью ![]() : (а) структурная схема и групповая
задержка, (б) нули коэффициента передачи
: (а) структурная схема и групповая
задержка, (б) нули коэффициента передачи
4. Численные и экспериментальные
результаты для фильтра с 6-ю резонаторами с ![]()
Для практических приложений наиболее интересным является случай введения отрицательной некаскадной связи между первым и последним резонаторами в фильтре 6-го порядка, где единственная некаскадная связь производит одновременно пару нулей на мнимой оси и пару нулей на действительной оси комплексной плоскости, что позволяет одновременно улучшить избирательность фильтра и линейность фазы. В таком фильтре имеется минимальное усложнение схемы по сравнению с обычным чебышевским фильтром.
Для экспериментальной проверки выводов исследования был
спроектирован, изготовлен и протестирован фильтр с 6-ю резонаторами с
дополнительной некаскадной связью ![]() , имеющий центральную частоту f0=2642,5 МГц. Технические требования для данного
фильтра были следующими: рабочая полоса частот 18 МГц, Ксв£1,2, вносимые потери в рабочей полосе
частот не более 1,2 дБ, вариации ГВЗ в рабочей полосе частот не более 3 нс,
ослабление не менее 10 дБ на частотах f0±20 МГц.
Полоса фильтра была выбрана от 2628,5 МГц до 2656,5 МГц (добавлено по 5 МГц с
каждого края рабочего диапазона частот). Структура фильтра была симметричной и
эквивалентная схема фильтра имела следующие параметры:
, имеющий центральную частоту f0=2642,5 МГц. Технические требования для данного
фильтра были следующими: рабочая полоса частот 18 МГц, Ксв£1,2, вносимые потери в рабочей полосе
частот не более 1,2 дБ, вариации ГВЗ в рабочей полосе частот не более 3 нс,
ослабление не менее 10 дБ на частотах f0±20 МГц.
Полоса фильтра была выбрана от 2628,5 МГц до 2656,5 МГц (добавлено по 5 МГц с
каждого края рабочего диапазона частот). Структура фильтра была симметричной и
эквивалентная схема фильтра имела следующие параметры: ![]() =50 Ом,
=50 Ом, ![]() =284,21 нГн,
=284,21 нГн, ![]() =1,28´10-2 пФ,
=1,28´10-2 пФ, ![]() =1,22,
=1,22, ![]() 3,14 нГн,
3,14 нГн, ![]() 2,04 нГн,
2,04 нГн, ![]() 2,01 нГн,
2,01 нГн, ![]() -0,35 нГн. Нули коэффициента передачи
НЧ-прототипа расположены в точках комплексной плоскости ±1,0423 и ±i1,5666.
-0,35 нГн. Нули коэффициента передачи
НЧ-прототипа расположены в точках комплексной плоскости ±1,0423 и ±i1,5666.
Эквивалентная схема фильтра с идеальными
трансформаторами на входе/выходе и взаимно-индуктивными связями контуров может
быть преобразована в хорошо известную схему с частотно-независимыми
К-инверторами сопротивлений [20]. При этом инверторы внешних связей равны ![]() , а инверторы внутренних связей равны
, а инверторы внутренних связей равны ![]() . Переход от эквивалентной схемы
фильтра с К-инверторами к фильтру с распределенной структурой производился по
известной методике [20].
. Переход от эквивалентной схемы
фильтра с К-инверторами к фильтру с распределенной структурой производился по
известной методике [20].
Для реализации был выбран фильтр с коаксиальными резонаторами
гребенчатого типа, в котором все настроечные винты для резонаторов находятся на
одной стороне корпуса. Внутренняя конструкция гребенчатого фильтра показана на рис.
5. Резонаторы имели поперечное сечение 30 мм ´ 30 мм и высоты 18 мм. Круглые стержни для резонаторов (внутренние проводники коаксиальных
резонаторов) имели внешние диаметры Æ8,5 мм, высоты 13 мм и диаметры отверстий Æ 7 мм. Для каскадных связей использовались индуктивные диафрагмы между
резонаторами. Внешние связи для фильтра были реализованы с помощью разъемов SMA
(3,5 × 1,5 мм), которые соединены кондуктивно (посредством пайки) медным
проводом Ø1 мм со стержнями 1-го и 6-го резонаторов. Некаскадная связь ![]() (емкостная связь) была обеспечена с
помощью короткого отрезка полужесткого коаксиального кабеля, уложенного в вырез
внутренней стенки корпуса между резонаторами 1 и 6 (оплетка кабеля была
припаяна к корпусу). Внутренние проводники кабеля были выпущены в виде зондов в
эти резонаторы. Величина связи подстраивалась путем подрезки длины зондов. Знак
связи (отрицательный) обеспечивался автоматически при таком элементе связи.
Настройка фильтра выполнялась с помощью настроечных винтов М5.
(емкостная связь) была обеспечена с
помощью короткого отрезка полужесткого коаксиального кабеля, уложенного в вырез
внутренней стенки корпуса между резонаторами 1 и 6 (оплетка кабеля была
припаяна к корпусу). Внутренние проводники кабеля были выпущены в виде зондов в
эти резонаторы. Величина связи подстраивалась путем подрезки длины зондов. Знак
связи (отрицательный) обеспечивался автоматически при таком элементе связи.
Настройка фильтра выполнялась с помощью настроечных винтов М5.
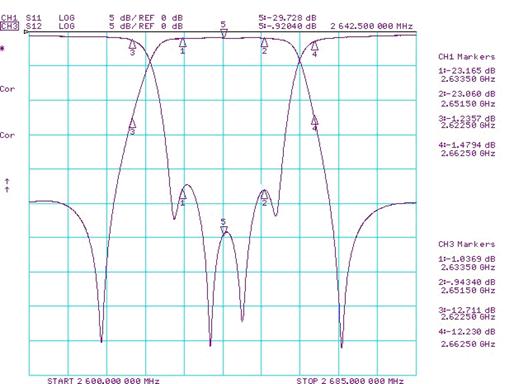
Теоретические результаты для эквивалентной схемы и результаты измерения для гребенчатого фильтра показаны на рис. 6 и 7. Измеренные вариации ГВЗ в рабочей полосе частот составили не более 2,5 нс. Для сравнения, обычный чебышевский фильтр с 6-ю резонаторами с той же полосой пропускания и теми же обратными потерями в полосе пропускания имел бы вариации ГВЗ порядка 6…7 нс. Измеренные вносимые потери в рабочей полосе частот составили менее 1 дБ для покрытых серебром частей фильтра, что соответствует добротностям резонаторов порядка 3500.
С помощью тепловой камеры проводились измерения температурных
сдвигов полосы пропускания фильтра. Корпус фильтра был изготовлен из алюминия,
стержни коаксиальных резонаторов были изготовлены из обычной стали, настроечные
винты М5 были изготовлены из нержавеющей стали (выбор материалов был сделан на
основании заранее проведенного температурного расчета для резонансной частоты
отдельного резонатора). Измеренный тепловой сдвиг составил ![]() 0,3 МГц для Dt=±50º C и гарантировал, что технические требования по
избирательности и вариациям ГВЗ выполнены и в диапазоне температур от -30 до
+70ºС.
0,3 МГц для Dt=±50º C и гарантировал, что технические требования по
избирательности и вариациям ГВЗ выполнены и в диапазоне температур от -30 до
+70ºС.
5. Выводы
Были исследованы структуры полосовых фильтров 4,6,8 и 10-го порядков с несоседними связями с целью исследования возникающих комплексных нулей передачи. Было найдено, что в фильтрах с 6-ю и 10-ю резонаторами с дополнительной отрицательной связью между первым и последним резонаторами существует возможность одновременно получить эллиптическую характеристику и улучшить линейность фазы в полосе пропускания. Для практики наиболее интересен фильтр 6-го порядка. Экспериментальные результаты для гребенчатого фильтра 6-го порядка с дополнительной отрицательной связью подтвердили выводы аналитического исследования. Если на входе и выходе базисной структуры с 6-ю резонаторами, имеющей улучшенную линейность фазы, подключить дополнительные резонаторы, то селективность фильтра может быть еще увеличена.
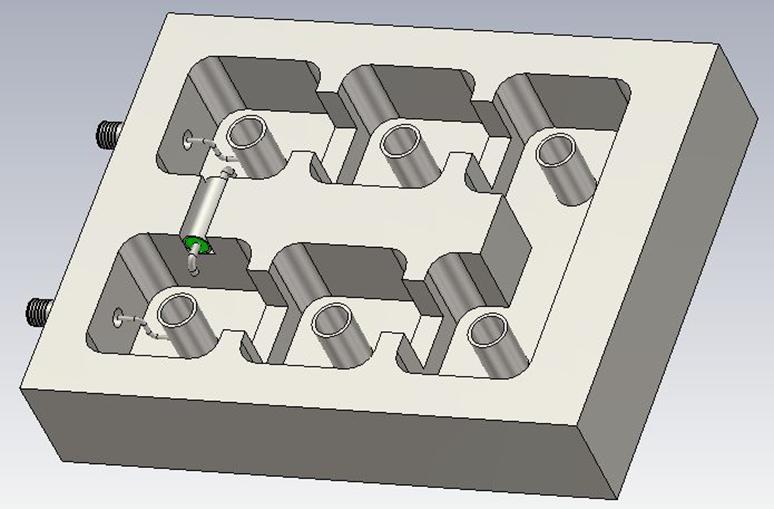
Рис. 5. Внутренняя конструкция гребенчатого фильтра
(а)

(б)
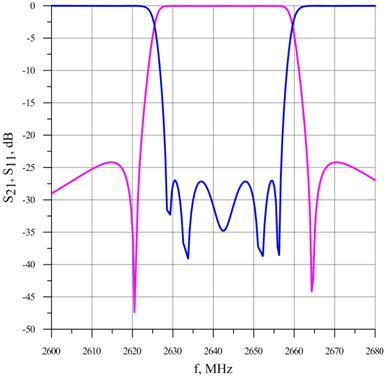
Рис. 6. Теоретические результаты
(эквивалентная схема) для фильтра с 6-ю резонаторами с ![]() : (а) коэффициент передачи и обратные
потери, (б) ГВЗ
: (а) коэффициент передачи и обратные
потери, (б) ГВЗ
(а)

(б)
Рис. 7. Экспериментальные результаты для гребенчатого
фильтра с 6-ю резонаторами с ![]() : (а)
коэффициент передачи и обратные потери, (б) ГВЗ
: (а)
коэффициент передачи и обратные потери, (б) ГВЗ
6. Приложение
Получим аналитическое выражение для ГВЗ фильтра и покажем, что нули коэффициента передачи прототипа на действительной оси комплексной плоскости создают локальный экстремум групповой задержки на центральной частоте фильтра, что приводит к уменьшению вариаций ГВЗ в полосе фильтра.
Для физически симметричной структуры полосового фильтра коэффициент четного порядка передачи низкочастотного прототипа может быть представлен в виде:
![]() (11)
(11)
где ![]() - четный полином,
- четный полином, ![]() - полиномом Гурвица порядка N,
- полиномом Гурвица порядка N, ![]() - нормированная комплексная частота
прототипа. Тогда коэффициент передачи по мощности и безразмерное групповое
время задержки для низкочастотного прототипа равны
- нормированная комплексная частота
прототипа. Тогда коэффициент передачи по мощности и безразмерное групповое
время задержки для низкочастотного прототипа равны
![]() , (12)
, (12)
где ![]() есть фаза коэффициента передачи (11). Эта фаза
зависит только от полинома Гурвица в знаменателе (11), так как полином числителя
является четной функцией. После ряда трансформаций может быть записано
выражение для ГВЗ как функции полинома Гурвица
есть фаза коэффициента передачи (11). Эта фаза
зависит только от полинома Гурвица в знаменателе (11), так как полином числителя
является четной функцией. После ряда трансформаций может быть записано
выражение для ГВЗ как функции полинома Гурвица ![]() :
:
![]() . (14)
. (14)
Анализ (14) показывает, что полиномы числителя и знаменателя
имеют порядки (2N-2) и 2N соответственно. Поскольку для
фильтров с хорошим Ксв в полосе пропускания имеются небольшие пульсации
коэффициента передачи ![]() , то можно приближенно считать, что в полосе
пропускания
, то можно приближенно считать, что в полосе
пропускания ![]() . Тогда можно приближенно представить
. Тогда можно приближенно представить ![]() в полосе пропускания следующим
образом:
в полосе пропускания следующим
образом:
![]() . (15)
. (15)
Полином ![]() имеет комплексные нули на
комплексной плоскости переменной
имеет комплексные нули на
комплексной плоскости переменной ![]() . Поэтому на мнимой оси
комплексной плоскости имеются соответствующие минимумы
. Поэтому на мнимой оси
комплексной плоскости имеются соответствующие минимумы ![]() . Следовательно, полином знаменателя
в (15) производит локальные максимумы или подъемы для
. Следовательно, полином знаменателя
в (15) производит локальные максимумы или подъемы для ![]() в окрестностях комплексных нулей
коэффициента передачи. Если нули передачи находятся на действительной оси
комплексной плоскости переменной
в окрестностях комплексных нулей
коэффициента передачи. Если нули передачи находятся на действительной оси
комплексной плоскости переменной ![]() , то локальный максимум
, то локальный максимум
![]() расположен на центральной частоте фильтра.
расположен на центральной частоте фильтра.
Литература
1. Kurzrok, R.M.: “General four-resonator filters at microwave frequencies”, IEEE Trans., 1966, MTT-14, No.6, pp.295-296.
2. Atia, A.E., and Williams, A.E.: "Narrow-bandpass waveguide filters", IEEE Trans., 1972, MTT-20, No.4, pp.258-265.
3. Atia, A.E., Williams, A.E., and Newcomb, R.W.: "Narrow-band multiple-coupled cavity synthesis", IEEE Trans., 1974, CAS-21, No.5, pp.649-655.
4. Thomas, J.B.: “Cross-coupling in coaxial cavity filters- a tutorial overview”, IEEE Trans., 2003, MTT-51, No.4, pp.1368-1376.
5. Rhodes, J.D.: “The theory of generalized interdigital networks”, IEEE Trans., 1969, CT-16, No.4, pp.280-288.
6. Rhodes, J.D.: “The design and synthesis of a class of microwave bandpass linear phase filters”, IEEE Trans., 1969, MTT-17, No.4, pp.189-204.
7. Rhodes, J.D.: “A low-pass prototype network for microwave linear phase filters”, IEEE Trans., 1970, MTT-18, No.6, pp.290-301.
8. Rhodes, J.D.: “The generalized interdigital linear phase filter”, IEEE Trans., 1970, MTT-18, No.6, pp.301-307.
9. Rhodes, J.D.: “The generalized direct-coupled cavity linear phase filter”, IEEE Trans., 1970, MTT-18, No.6, pp.308-313.
10. Cloete, J.H.: “Tables for nonminimum-phase even-degree low-pass prototype networks for the design of microwave linear-phase filters”, IEEE Trans., 1979, MTT-27, No.2, pp.123-128.
11. Wenzel, R.J.: “Solving the approximation problem for narrowband bandpass filters with equal-ripple passband response and arbitrary phase response”, 1975 MTT-S Int. Symposium Digest, 1975, p.50.
12. Levy, R.: “Filters with single transmission zeroes at real or imaginary frequencies”, IEEE Trans., 1976, MTT-24, No.4, pp.172-181.
13. Cameron, R.J., and Rhodes, J.D.: “Asymmetric realizations for dual-mode bandpass filters”, IEEE Trans., 1981, MTT-29, No.1, pp.51-58.
14. Pfitzenmaier, G.: “Synthesis and realization of narrow-band canonical microwave bandpass filters exhibiting linear phase and transmission zeros”, IEEE Trans., 1982, MTT-30, No.9, pp.1300-1311.
15. Macchiarella, G.: “An original approach to the design of bandpass cavity filters with multiple couplings”, IEEE Trans., 1997, MTT-45, No.2, pp.179-187.
16. Cameron, R.J.: “General coupling matrix synthesis methods for Chebyshev filtering functions”, IEEE Trans., 1999, MTT-47, No.4, pp.433-442.
17. Cameron, R.J.: “Advanced coupling matrix synthesis techniques for microwave filters”, IEEE Trans., 2003, MTT-51, No.1, pp.1-10.
18. Yildirim N., Sen O.A., Sen Y., Karaaslan M., Pelz D. “A revision of cascade synthesis theory covering cross-coupled filters”, IEEE Trans., 2002, MTT-50, No.6, pp.1536-1543.
19. Корн Г. Справочник по высшей математике для научных работников и инженеров. М. Наука, 1977.
20. Matthaei G.L., Yong L., Jones E.M.T. Microwave filters, impedance-matching networks, and coupling structures. Artech house, 1980.