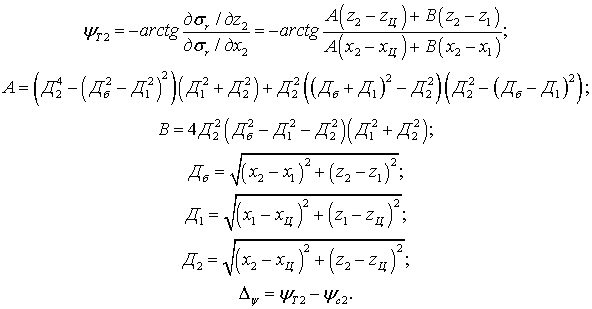УДК 629.7.058.53

АЛГОРИТМ ТРАЕКТОРНОГО УПРАВЛЕНИЯ НАБЛЮДЕНИЕМ
В ДВУХПОЗИЦИОННОЙ ПАССИВНОЙ СИСТЕМЕ НАВЕДЕНИЯ ВОЗДУШНОГО БАЗИРОВАНИЯ
НА ОСНОВЕ МЕТОДА ПРОЕКЦИИ ГРАДИЕНТА

В. И. Меркулов, Д. А. Миляков, В. С. Чернов

Акционерное общество «Концерн радиостроения «Вега»

Статья получена 23 апреля 2015 г.

 

Аннотация: в статье приводятся результаты разработки на основе градиентного метода и метода проекции градиента алгоритмов траекторного управления для летательных аппаратов информационной поддержки в составе двухпозиционных систем наведения, обеспечивающих минимально возможную ошибку определения местоположения цели в любой момент времени.

Ключевые слова: источник радиоизлучения, алгоритм траекторного управления, самолет информационной поддержки, ошибка определения местоположения, градиентный метод.

Abstract. The article presents the results of the development on the basis of the gradient method and the method of gradient projection algorithms for trajectory control of aircraft information support as a part of two-position guidance system to ensure the lowest error in determining the location of the target at any given time.

Keywords: radio source, trajectory control algorithm, the plane information support, error location, the gradient method.

 

Развитие бортовых радиоэлектронных систем летательных аппаратов военного назначения неразрывно связано с возрастанием роли пассивных режимов их функционирования, что обусловлено действием ряда факторов.

Во-первых, в процессе ведения боевых действий для предотвращения поражения воздушных, наземных и морских целей будут широко использоваться средства радиоэлектронной борьбы. При современном состоянии техники радиоэлектронного противодействия вероятны ситуации, когда на летательных аппаратах каналы дальности и скорости в однопозиционных бортовых РЛС будут подавлены. При этом бортовые РЛС смогут измерять лишь угловые координаты источников помеховых радиосигналов.

Во-вторых, в настоящее время большая роль отводится системам контроля (радиомониторинга) источников радиоизлучения (ИРИ), основу которых составляют средства радио- и радиотехнической разведки (РРТР) летательных аппаратов (ЛА). Данные средства в однопозиционном варианте также могут измерять лишь угловые координаты ИРИ.

Для решения задачи информационного обеспечения процесса наведения ЛА от АК РЛДН в указанных условиях необходимо выполнять наблюдение целей на базе многопозиционных РЛС (МПРЛС). При этом одной из основных задач является траекторное управление наблюдением, с помощью которого обеспечивается формирование оценок фазовых координат целей с необходимой точностью [1-5].

Наиболее простым вариантом МПРЛС являются угломерные двухпозиционные радиолокационные системы (ДПРЛС), позволяющие достаточно быстро оценивать дальности до радиоизлучающих целей и скорости сближения с ними либо прямоугольные координаты целей и их производные.

Для эффективного функционирования ДПРЛС разработаны различные алгоритмы траекторного управления летательными аппаратами [1-5], входящими в состав двухпозиционной системы наведения. Реализация большинства известных алгоритмов наведения летательных аппаратов предполагает разделение их в зависимости от характера выполняемых боевых задач на ударный ЛА и на ЛА информационного обеспечения. Ударный ЛА осуществляет самонаведение на радиоизлучающую цель. Летательный аппарат информационного обеспечения (информационной поддержки) должен выходить на проходящий через цель перпендикуляр к линии ударный ЛА-цель, при движении по которому достигается минимизация ошибок определения местоположения цели. При этом возможны случаи вывода ЛА информационного обеспечения в произвольную точку либо заданную точку перпендикуляра с упреждением и без упреждения [1-5].

Основным недостатком указанных методов является тот обстоятельство, что до выхода ЛА информационного обеспечения в точку, лежащую на перпендикуляре, к текущим значениям ошибок определения местоположения цели не предъявляется никаких специальных требований. В то же время процесс самонаведения ударного ЛА может закончиться еще до момента выхода ЛА информационного обеспечения на перпендикуляр к линии ударный ЛА-цель.

Поскольку решение задачи обеспечения одновременного выхода ударного ЛА в точку применения оружия, а ЛА информационной поддержки в произвольную либо заданную точку на указанном выше перпендикуляре представляет собой определенные трудности, то целесообразно организовать управление ЛА информационной поддержки таким образом, чтобы ошибка определения местоположения цели в любой момент времени была минимально возможной. Для выполнения данного условия необходимо обеспечить движение ЛА информационной поддержки по специальной траектории, параметры которой могут быть рассчитаны по формулам, полученным на основе теории принятия решений в одношаговых задачах оптимального управления [6].

Ниже приводятся результаты разработки алгоритмов траекторного управления парой самолетов для различных тактических ситуаций.

В состав двухпозиционной системы наведения (ДПСН) входят два наводимых ЛА. В качестве ЛА (наводимых приемных позиций) для конкретности будем рассматривать самолеты-истребители. Бортовые РЛС этих самолетов объединяются в группу, образуя пассивную угломерную ДПРЛС, работающую по источникам радиоизлучений (ИРИ).

В общем случае необходимо организовать наведение самолетов в двух плоскостях: горизонтальной и вертикальной. В дальнейшем для простоты будем рассматривать управление только в горизонтальной плоскости. Функционирование системы наведения в такой ситуации осуществляется следующим способом.

Источник излучения, пространственно совпадающий с целью, формирует радиосигналы, принимаемые в первой и второй приемных позициях. Угломеры, входящие в состав пассивных бортовых РЛС или систем РРТР и часто называемые пеленгаторами, измеряют бортовые пеленги цели  и  в каждой приемной позиции. Их навигационные системы счисляют местоположение приемных позиций ( и ) в прямоугольной системе координат и измеряют курсы ,  самолетов. Указанные координаты и параметры движения образуют минимально необходимый набор измеряемых величин. Измеренные значения пеленгов цели, прямоугольных координат приемных позиций и курсов самолетов с помощью аппаратуры передачи данных передаются с приемных позиций на пункт управления либо приемные позиции обмениваются результатами измерений между собой. Результаты измерения пеленгов цели в двух разных позициях, прямоугольных координат и курсов самолетов поступают в вычислительную систему пункта  управления либо вычислительные системы самолетов, где формируются оценки координат и параметров движения цели на основе одного из известных алгоритмов [7]. Вместо данных о бортовых пеленгах цели и курсах ЛА могут передаваться азимуты цели, что позволяет сократить объем передаваемой по радиоканалам информации. В вычислительных системах приемных позиций вырабатываются параметры требуемого движения наводимых самолетов. При наличии пункта управления в его вычислительной системе формируются параметры требуемого движения наводимых самолетов, передаваемые соответственно на ударный самолет и самолет информационного обеспечения.

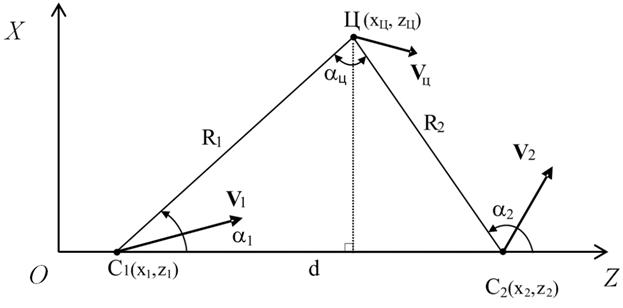
Для оценивания координат и параметров движения цели на борту самолетов либо центра управления предварительно выполняют косвенные измерения координат радиоизлучающей цели триангуляционным способом [7]. При этом местоположение цели определяется точкой пересечения двух прямых, каждая из которых является линией положения, т.е. геометрическим местом точек возможного местонахождения источника излучения. Для определения пространственных координат цели достаточно измерить азимуты a₁ и a₂ в двух пунктах (рис. 1).

 

 

Рис. 1. Геометрия взаимного расположения приемных позиций
и источника радиоизлучения

 

На рисунке 1 точка Ц характеризует положение цели в пространстве, а точки С₁ и С₂ показывают положение двух самолётов (подвижных позиций) в момент измерения углов в прямоугольной системе координат ОXZ, в которой ось ОX совпадает с базой d. Положение точки С₁ на рисунке совпадает с началом системы координат.

Применительно к горизонтальной плоскости при пеленгации источника излучения, расположенного в точке Ц, из двух точек С₁ и С₂, отстоящих друг от друга на расстояние d, координаты источника определяются путем решения треугольника С₁ЦС₂ по двум углам a₁, a₂ и основанию d с помощью следующих соотношений [3, 7]:

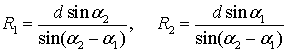,                         (1)

 

где углы a₁ и a₂ отсчитываются в точках С₁ и С₂ относительно направления базы пеленгации.

На рисунке введены следующие обозначения:  – координаты цели в горизонтальной плоскости, a₁ и a₂ – азимуты цели относительно двух самолетов,  и  – расстояния до радиоизлучающей цели от самолетов; x₁, z₁ и x₂, z₂ – прямоугольные координаты самолетов,  и  – скорости самолетов,  – угол пересечения линий визирования; d – база пеленгации (линия, соединяющая самолеты С₁ и С₂).

На основе заложенных в вычислительную систему критериев назначения самолетов выбирается ударный самолет для атаки воздушной цели и самолет информационного обеспечения, позволяющий создать наилучшие условия проведения радиолокационных наблюдений радиоизлучающей цели. В вычислительных системах вырабатываются параметры управления  и  самолетами в зависимости от задач, возлагаемых на конкретный самолет. При наличии пункта управления соответствующие параметры вырабатываются в его вычислительной системе, которые затем передаются на самолеты в виде команд наведения с помощью командной радиолинии управления.

Особенностью процедуры определения местоположения ИРИ является тот факт, что точность оценивания местоположения цели зависит от «геометрии» взаимного положения наводимых самолетов и цели, а также от точности измерений. В частности, при одинаковой точности измерения бортовых пеленгов, точность определения местоположения излучающей цели определяется среднеквадратической ошибкой (СКО) [3, 7]

                                            (2)

где  – СКО измерения пеленгаторами бортовых пеленгов цели в градусах с позиций  и .

Отсюда следует, что точностью определения местоположения цели можно управлять, влияя на расположение приемных позиций на плоскости. Для этого при разработке алгоритмов траекторного управления истребителями применительно к рассматриваемой системе наведения необходимо использовать концепцию траекторного управления наблюдением. Суть этой концепции состоит в том, что наряду с решением основной задачи – перехвата движущихся ИРИ двухпозиционные системы способны за счёт целенаправленного управления пространственным положением одной или обеих позиций обеспечить наивысшую точность определения местоположения объекта поражения, а соответственно и наивысшую точность наведения.

Выражение (2) показывает, что точность определения местоположения излучающего объекта зависит не только от ошибок пеленгации, характеризующихся значением, но и от взаимного расположения позиций и целей, определяемого значением угла  расстояниями R₁ и R₂ до цели от приемных позиций.

В общем случае задача формирования управления обеими позициями, одновременно обеспечивающего и повышение точности определения местоположения радиоизлучающей цели и ее уничтожение, является достаточно сложной [1-5]. Задача оптимизации управления пассивной ДПСН, как указывалось выше, существенно упрощается, если функции перехвата излучающей цели и обеспечения максимальной точности определения ее местоположения разделить между носителями С₁ и С₂. При таком подходе одна из позиций, например, наиболее близкая к цели, решает задачу наведения, используя тот или иной известный метод наведения, а вторая – целенаправленно изменяет свое положение в пространстве, обеспечивая на обеих позициях максимально высокую точность определения местоположения перехватываемого объекта.

Ниже описывается алгоритм траекторного управления самолетом информационной поддержки, обеспечивающий управление им таким образом, чтобы ошибка определения местоположения цели в любой момент времени была минимально возможной. Этот алгоритм основан на использовании теории нелинейного программирования и не учитывает ограничения на траекторию полета самолета информационной поддержки. При применении ДПСН возможны ситуации, когда на траекторию полета ЛА информационной поддержки обеспечения накладываются определенные ограничения в виде неравенств. В этом случае алгоритмы траекторного управления могут быть найдены на основе метода проекции градиента целевой функции.

 

Алгоритм траекторного управления самолетом информационного обеспечения на основе градиентного метода

Для определения требуемой траектории движения самолета обеспечения воспользуемся градиентным методом поиска минимума целевой функции. Градиентом функции , обозначаемым grad или , называется вектор, величина которого определяет скорость изменения функции , а направление совпадает с направлением наибольшего возрастания этой функции. Вектор –, указывающий направление наибольшего убывания функции , называется антиградиентом функции . Пусть -мерный векторный аргумент  определяет состояние управляемого объекта (самолета информационного обеспечения). Тогда градиент функции будет представлять вектор-столбец вида

= grad.                             (3)

 

Стратегия градиентного метода представляет собой последовательность шагов, каждый из которых содержит две операции:

1) определение направления наибольшей крутизны спуска, т.е. направления антиградиента функции ;

2) перемещение в выбранном направлении на заданное расстояние.

Математически стратегия градиентного метода получается, если перемещение  на каждом шаге вдоль каждой из осей будет пропорционально составляющей градиента  в направлении этой оси:

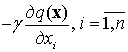=.                                                       (4)

 

При этом поправка на -м шаге решения задачи может быть представлена в виде

.                                                         (5)

Стратегия, выражаемая соотношением (5), определяет движение с переменным шагом, так как значение шага определяется значением градиента . Организовать полет самолета с переменным шагом достаточно сложно. Поэтому будем использовать градиентную стратегию с постоянным шагом, значение которого равно , где  – скорость самолета. В этом случае поправка на каждом шаге определяется по формуле

,                                                          (6)

получающейся из (5) заменой вектора градиента  на вектор направления градиента

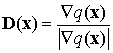,                                                                  (7)

 

где

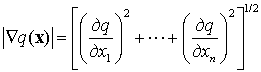                                    (8)

представляет собой модуль градиента .

Отметим, что вектор первичных наблюдаемых параметров наряду с азимутами цели  в точках пеленгации содержит также прямоугольные координаты x₁, z₁ и x₂, z₂, скорости  и  и курсы ,  самолетов С₁ и С₂.

При траекторном управлении самолетом информационного обеспечения в качестве целевой функции целесообразно выбрать среднюю квадратичную ошибку местоопределения  (2). В этом случае переменными состояния (компонентами вектора состояния) являются прямоугольные координаты x₂, z₂ самолета С₂ информационного обеспечения. Выражение (2) в явном виде не зависит от этих координат, поэтому его необходимо преобразовать к виду, удобному для нахождения градиента целевой функции. Ниже приводятся необходимые для этого соответствующие уравнения связи.

, ,         (9)

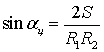,                                                                         (10)

 

где     – площадь треугольника С₁ЦС₂,

 – полупериметр этого треугольника;

 – расстояние между приемными позициями (база пеленгации).

Если подставить указанные выражения в (2), то получим зависимость целевой функции от прямоугольных координат цели и самолетов. Для получения аналитического выражения градиента целевой функции необходимо взять частные производные  и  целевой функции  по прямоугольным координатам x₂, z₂ самолета информационного обеспечения С₂. В результате выполнения данной процедуры получаются достаточно громоздкие выражения, которые здесь не приводятся. Поэтому на практике можно воспользоваться численным способом нахождения частных производных.

После вычисления частных производных требуемый курс самолета информационного обеспечения и параметр управления им рассчитываются по формулам

                 (11)

Алгоритм (11) траекторного управления самолетом информационной поддержки обеспечивает получение наибольшего убывания среднего квадрата ошибки местоопределения радиоизлучающей цели и, тем самым, удовлетворяет предъявленным требованиям. Достоинство данного алгоритма состоит в том, что убывание среднего квадрата ошибки местоопределения радиоизлучающей цели обеспечивается не только за счет изменения угла , но и в результате уменьшения расстояний R₁ и R₂.

 

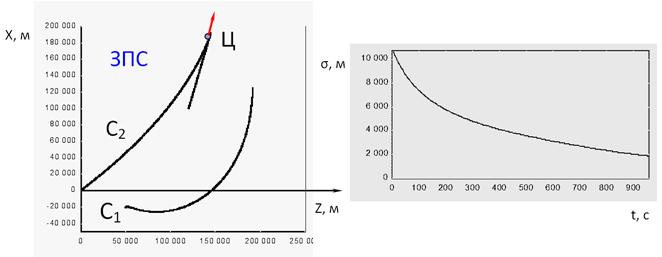
Рис. 2,а.

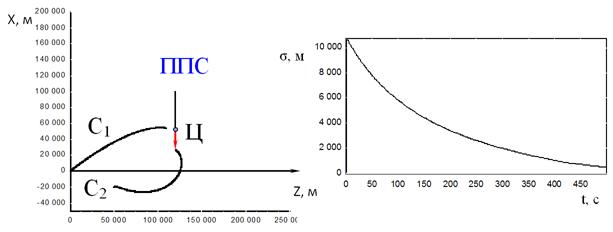
Рис. 2,б.

 

На рис. 2 приведены траектории движения ударного самолета С₁, самолета информационного обеспечения С₂ и цели в горизонтальной плоскости для гипотетических вариантов в задней и передней полусферах (ЗПС и ППС), а также эволюции во времени ошибки  определения местоположения цели [3].

В начальный момент времени самолеты С₁ и С₂  находятся в точках с координатами x₁(0)=0 км, z₁(0)=0 км и x₂(0)=0 км, z₂(0)=50 км, соответственно, а цель – в точке с координатами 100 км,125 км. Скорости самолетов =200 м/с и =300 м/с.

 

Алгоритм траекторного управления самолетом информационного обеспечения на основе метода проекции градиента

Данный метод применяется в задачах оптимизации с ограничениями в виде неравенств [6]. В нашем случае эти ограничения задаются допустимой областью нахождения самолета информационной поддержки.

Под допустимой областью  понимается область -мерного пространства, в которой выполняются ограничения, наложенные на переменные . В начальный момент времени самолет находится в допустимой области . При нахождении самолета в допустимой области рассматриваемый метод является обычным градиентным методом. После выхода на границу области  в некоторой граничной точке , , движение в направлении антиградиента – может вывести самолет за пределы допустимого множества. Поэтому антиградиент проецируется на линейное многообразие М, аппроксимирующее участок границы в окрестности точки . Двигаясь в направлении проекции вектора – на многообразие М, отыскивают новую точку , в которой , принимают  за исходное приближение и продолжают процесс. Опишем данную процедуру более подробно.

В точке  часть ограничений-неравенств удовлетворяются как равенство:

,                                                    (12)

 – где общее число ограничений-неравенств.

Такие ограничения называются активными.

Обозначим через  набор индексов  этих ограничений. Их уравнения соответствуют гиперповерхностям, образующим границу области  в окрестности точки . В общем случае эта граница является нелинейной. Ограничения , аппроксимируются гиперплоскостями, касательными к ним в точке :

.

 

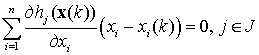Полученные гиперплоскости ограничивают некоторый многогранник М, аппроксимирующий допустимую область  в окрестности точки .

Проекция  антиградиента – на многогранник вычисляется по формуле

.                                                           (13)

Здесь Р – оператор ортогонального проектирования, определяемый выражением

,                                                          (14)

где  – единичная матрица размером ;  – матрица размеров . Она образуется транспонированными векторами-градиентами , , активных ограничений. Далее осуществляется спуск в выбранном направлении:

.                                                        (15)

Метод проекции градиента можно использовать для нахождения алгоритма траекторного управления в ситуациях, когда на полет самолета информационного обеспечения С₂ (рисунок 1) накладываются определенные ограничения. В частности, они могут быть обусловлены требованием к самолету С₂ не находиться в зоне возможных пусков ракет самолета противника.

Для упрощения решаемой задачи будем полагать, что известна дальность  стрельбы самолетом противника, которая может меняться в зависимости от ракурса сближения с целью. Данное допущение позволяет считать, что самолет С₂ не должен приближаться к цели на расстояние меньшее, чем . Тогда допустимая область  для самолета С₂ может быть охарактеризована ограничением-неравенством вида

.

Активное ограничение имеет форму

или

.                                                                      (16)

В результате сравнения (12) и (16) приходим к выводу, что в данном случае , а матрица А представляет собой вектор

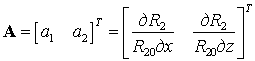,                                         (17)

где , .

 

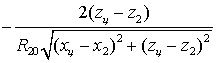На основе (14) и (16) может быть найден оператор Р ортогонального проектирования 

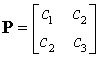,                                                                       (18)

 

в котором

, , .

 

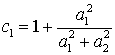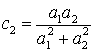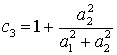Используя (13), (17) и (18), получим выражение для проекции р вектора антиградиента на границу допустимой области:

,

где , .

Требуемый курс для самолет С₂ рассчитывается аналогично (11)

.

 

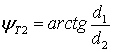Таким образом, полученный алгоритм траекторного управления самолетом информационной поддержки, использующий метод проекции градиента, предотвращает вход самолета в опасную зону. Недостаток алгоритма состоит в том, что проекция градиента начинает рассчитываться, когда самолет С₂ находится в точке, где выполняется равенство (16). В силу инерционности самолета он может выйти из допустимой области. Поэтому алгоритм траекторного управления должен быть доработан либо можно воспользоваться алгоритмом траекторного управления, полученного на основе метода барьерных функций [6].

Следует отметить, что общим недостатком концепции управления позициями в ДПСН, основанной на разделении функций между летательными ЛА на ударные и информационные, является достаточно большое время, необходимое для достижения минимума ошибки (2), а соответственно, и низкая точность определения местоположения ИРИ на начальных участках траектории наведения в случае малых начальных значениях угла α_ц. Для устранения данного недостатка на основе статистической теории оптимального управления и нелинейного программирования разработаны методы и соответствующие алгоритмы траекторного управления обеими позициями, направленные на обеспечение наивысшей точности определения координат и параметров движения ИРИ и лишь после этого на решение задачи наведения [1-5]. Использование в указанной ситуации вместо градиентного метода разработанного метода проекции градиента позволит осуществлять не только траекторное управление наблюдением, но и предотвращать вхождение ЛА в запретные зоны полета.

 

Выводы

Изложенное выше позволяет сделать следующие выводы:

1.     Алгоритм траекторного управления самолетом информационной поддержки, разработанный на основе градиентного метода минимизации целевой функции, позволяет в угломерной двухпозиционной системе наведения получить наибольшее убывание среднего квадрата ошибки местоопределения радиоизлучающей цели.

2.     Алгоритм траекторного управления самолетом информационной поддержки, использующий метод проекции градиента, повышает эффективность боевого применения угломерной двухпозиционной системе наведения, предотвращая вход самолета в опасную зону.

 

Работа выполнена при поддержке РФФИ, проект № 13-08-01127-а.

 

Литература

1. Меркулов В.И., Чернов В.С., Юрчик И.А. Авиационные многопозиционные системы радиоуправления. // Успехи современной радиоэлектроники. 2006. № 12.

2. Меркулов В.И., Куимов А.М., Чернов В.С. Траекторное управление пассивными двухпозиционными системами. // Информационно-вычислительные и управляющие системы. 2008. №12.

3.Абатуров В.А., Меркулов В.И., Чернов В.С. Авиационные системы радиоуправления. Многопозиционные системы радиоуправления. Учебное пособие. – М.: ВВИА им. проф. Н.Е Жуковского, 2008.

4. Белик Б.В., Белов С.Г., Верба В.С. и др. Авиационные системы радиоуправления / Под ред. В.С. Вербы, В.И Меркулова. Монография. – М.: Радиотехника, 2014. – 376 с.

5.Меркулов В.И., Чернов В.С. Анализ методов наведения двухпозиционными пассивными системами воздушного базирования на источники радиоизлучения. // Успехи современной радиоэлектроники. 2013. №7. С. 26-40.

6.Фурунжиев Р.И., Бабушкин Ф.М., Варавко В.В. Применение математических методов и ЭВМ: Практикум: Учеб. пособие для вузов. – Мн.: Выш. шк., 1988.

7. Верба В.С., Меркулов В.И., Дрогалин В.В. и др. Оценивание дальности и скорости в радиолокационных системах. Ч.3. / Под ред. В.С. Вербы, В.И. Меркулова. М.: Радиотехника. 2010.