Способ приема дискретных частотных сигналов первого порядка в канале с многолучевостью
И. В. Головкин
ФГОБУ ВПО МТУСИ
Статья получена 17 мая 2015 г.
Аннотация. В работе предложен способ приема дискретных частотных сигналов первого порядка в канале с многолучевостью. Рассмотрена реализация предложенного способа с использованием быстрого преобразования Фурье. Приведены результаты компьютерного моделирования сигнально-кодовой конструкции с использованием ДЧ сигналов и кодов Рида-Соломона.
Ключевые слова: дискретные частотные сигналы, КВ канал, многолучевость.
Abstract. In the paper the method of receiving discrete frequency signals in multipath channel is suggested. Realization of suggested method with fast Fourier transform is investigated. Results of computer simulation of discrete frequency signals with Reed-Solomon error correction codes in HF channel are presented.
Key words: discrete frequency signals, HF channel, multipath.
Введение
Дискретные частотные сигналы представляют собой последовательность радиоимпульсов, несущие частоты которых изменяются по определенному правилу [1]. Основным достоинством дискретных частотных сигналов как класса широкополосных сигналов является возможность получения достаточно высокой относительной скорости при ансамблях большого объема. При работе в многолучевом канале наиболее простым способом приема ДЧ сигналов является детектирование по квадрату огибающей элементов сигнала. Актуальным является вопрос повышения энергетической эффективности ДЧ сигналов за счет использования квазикогерентного приема в каналах с многолучевым распространением.
1. Постановка задачи
Положим, также как и
в [1], что ДЧ сигнал состоит из 
элементов, а все
элементы имеют одинаковую форму 
. Пусть номера
элементов 
изменяются от 0 до 
, 
- комплексная
амплитуда -го элемента 
-го ДЧ
сигнала , а положение -го элемента по частоте
определяется сдвигом, равным 
, где 
- шаг разноса по частоте, 
- символ частотной кодовой
последовательности, причем при изменении 
меняется в таких же пределах от 0 до M-1, но в определенном порядке.
Длительность импульса равна 
, а его ширина спектра 
[1].
Рис. 1 а) Расположение импульсов на
временной оси
б) Расположение импульсов на частотно-временной плоскости
На рисунке 1а над каждым импульсом указана его несущая частота. На частотно-временной плоскости (см. рисунок 1б) штриховкой выделены квадраты, в которых распределена энергия импульсов ДЧ. Как видно из рисунка 1б, энергия ДЧ распределена неравномерно на частотно-временной плоскости.
Комплексная огибающая ДЧ сигнала [1]:
У рассматриваемых далее ДЧ
сигналов первого порядка 
и форма 
имеет вид:
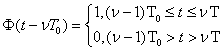
В
многолучевых каналах тропосферной и ионосферной радиосвязи, в КВ диапазоне, в
системах мобильной связи, сигнал, посланный передатчиком, приходит в точку
приема по различным путям (лучам). В результате этого на вход приемника вместо
переданного сигнала 
воздействует сумма составляющих,
называемых лучами:
где 
-
коэффициент передачи i-го луча; 
- относительная задержка i-го луча; L - число лучей; 
- фаза i-го луча.
Суть рассматриваемой проблемы – разработка алгоритма квазикогерентного приема ДЧ сигналов для каналов с многолучевым распространением.
2. Алгоритм приема
Известная структурная схема согласованного фильтра для ДЧ сигнала [1] приведена на рис.2.
При реализации правила оптимального разнесенного когерентного приема при одинаковой спектральной плотности мощности шума во всех ветвях требуется вычисление корреляционных интегралов с последующим суммированием [2]
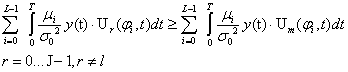
где 
-
объем ансамбля ДЧ сигналов, 
- среднеквадратичное
значение гауссовского шума, 
- сигнал 
у которого все спектральные составляющие
сдвинуты по фазе на . Таким образом, в схеме
согласованного фильтра для ДЧ сигнала на рис.2 каждый из фазовращателей должен
обеспечить сдвиг по фазе на -. Для этого необходимо
произвести оценку по каждому из частотных каналов ДЧ сигнала.
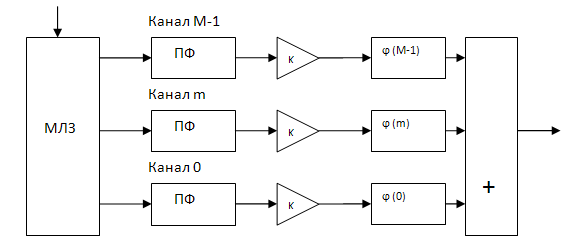
Рис. 2 Структурная схема согласованного фильтра для ДЧ сигнала.
МЛЗ - многоотводная линия задержки, ПФ –
полосовой фильтр, K - усилитель, 
- фазовращатели.
При неизвестных коэффициентах замираний и неизвестной фазе используется правило оптимального разнесенного некогерентного приема [2]
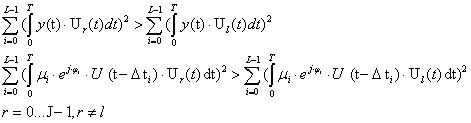
Далее будет рассматриваться двухлучевой канал, хотя результаты могут быть обобщены на большее число лучей и правило приема в соответствии с формулой 1.5 . Предположим что:
1) сформирован массив 
размерностью 
путем
взятия M отсчетов с выходов M-фильтров, согласованных с импульсами ДЧ сигнала на частотах 
, в моменты времени 
, где 
-момент взятия отсчета в значащей точке,
так что опорный сигнал синхронизирован с нулевым лучом т.е. 
(такое предположение упрощает формульные
соотношения);
2) относительная задержка первого луча мала по сравнению с
длительностью элементарного импульса ДЧ сигнала 
;
3) разнос частот кратен 
и существенно больше
минимально необходимого, 
.
Рассмотрим
способ вычисления корреляционный метрики с сигналом 
, для этого
сформируем вектор 
со снятой частотной модуляцией
путем выборки элементов из массива в соответствие с
законом ,
, . Сформируем переупорядоченный вектор 
по монотонному возрастанию частоты.
Вектор R будет иметь вид:
Видно, что R содержит две частотных составляющих и лучи могут быть выделены при помощи фильтрации.
Вычислим две величины:
сумму элементов вектора R
сумму
элементов вектора R предварительно поэлементно перемноженного с комплексной
синусоидой 
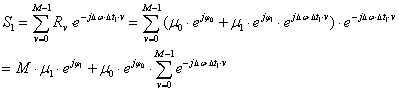
Подавление
составляющих с частотами, отличными от 0, определяется величиной 
. При зафиксированных и количестве элементов ДЧ сигнала коэффициент подавления второго луча
определяется АЧХ фильтра сумматора [3] и равен
.
Примером
модели двухлучевого канала является модель КВ канала в соответствии с
рекомендацией ITU [4]. На рис. 3 построено подавление для ДЧ c M=29 и разносом частот 400 Гц. Как видно
из рисунка, при выборе достаточно большой величины длительности элемента ДЧ
сигнала 
и обработке по формулам 1.7 и 1.8
уверенно может быть выделена разность хода лучей в диапазоне 0.2….2.3 мс, что
удовлетворяет моделям для средних широт в спокойном (0.5 мс), нормальном (1 мс)
и возбужденном состоянии ионосферы (2 мс) [4].
Рис. 3 Подавление дБ в зависимости от разности хода лучей для ДЧ сигнала с M=29 и разносом частот 400 Гц.
Для приближенного вычисления выражений 1.7 и 1.8, а также при реализации системы синхронизации ДЧ сигналов в канале с многолучевостью может быть использован аппарат быстрого преобразования Фурье. На рис.4 приведена предлагаемая структурная схема согласованного фильтра для ДЧ сигналов, прошедших двухлучевой канал.
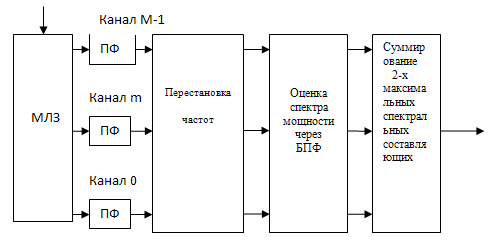
Рис. 4 Структурная схема согласованного фильтра для ДЧ сигнала, прошедшего двухлучевой канал.
Оценка наличия двух спектральных составляющих может производиться по преамбуле, обычно передаваемой в начале сообщения в системе связи.
В качестве ансамбля дискретно частотных сигналов далее использована усеченная композиционная система ДЧ сигналов [1], сформированная по следующему правилу:
где 
обозначает
-й элемент 
-й
кодовой последовательности; 
и 
; 
-
номер элемента в сигнале. Объем системы при выбранном 
равен M-1 [1], варьируя ,
можно сформировать ансамбль объемом до 
. Для
рассматриваемых ДЧ сигналов были выбраны M=29, r=5.
На рис.5 приведены результаты компьютерного моделирования сигнально-кодовой конструкции на основе укороченного кода Рида-Соломона n=256, k=128 в поле GF(512) и ансамбля ДЧ сигналов 29,29 объемом 512, разнос частот 400 Гц, длительность элемента 10 мс. Модель канала для средних широт и умеренных условий в соответствии со стандартом ITU-RF.1487. При квазикогерентном приеме использовался БПФ размерностью 32 точки. Оценка частот производилась по преамбуле длительностью 8 ДЧ сигналов передаваемой вначале сообщения.
Как видно
из рис.5, использование квазикогерентного приема обеспечивает энергетический
выигрыш для рассматриваемой сигнально-кодовой конструкции в размере 3 дБ для
вероятности ошибки на сообщение 
=0.1 (доверительный
интервал 
, с доверительной вероятностью
).
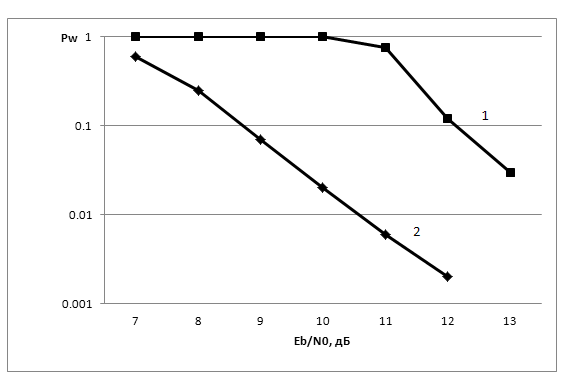
Рис.5 Вероятность
ошибки на сообщение ( ) для сигнально-кодовой
конструкции на основе укороченного кода Рида-Соломона n=256 k=128 в поле
GF(512) и ансамбля ДЧ сигналов 29,29 объемом 512, разность частот 400 Гц,
длительность элемента 10 мс. Модель канала для средних широт и умеренных
условий в соответствии со стандартом ITU-RF.1487 (разность хода лучей 1 мс,
Доплеровское расширения спектра 0.5 Гц). Кривая 1 детектирование по квадратам
огибающей элементарных импульсов, кривая 2 квазикогерентный прием с
использованием БПФ размерностью 32 точки.
Заключение
Приведено
описание алгоритма квазикогерентного приема ДЧ сигналов, прошедших многолучевой
канал. Предложена эффективная с вычислительной точки зрения процедура
приближенной реализации квазикогерентного приема с использованием БПФ. Путем
компьютерного моделирования сигнально-кодовой конструкции с использованием ДЧ
сигналов и кода Рида-Соломона показано наличие энергетического выигрыша в
размере 3 дБ для вероятности ошибки на сообщение =0.1 в
модели канала соответствующей рекомендации ITU-R F.1487.
Литература
1. Варакин Л.Е. Системы связи с шумоподобными сигналами, – М.: Радио и связь, 1985,384с.
2. Финк Л.М. Теория передачи дискретных сообщений. – М.: Советское радио, 1970. – 728с.
3. Ричард Лайонс. Цифровая обработка сигналов: Второе издание. Пер. С англ. – М.: ООО« Бином-Пресс», 2006. – 656 стр.
4. ITU-R F.1487. Testing of HF modems with bandwidths of up to about 12 kHz using ionospheric channel simulators, 2000, 13 p.