| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 11 , 2000 |
КЛАССИФИКАЦИОННЫЕ
ШКАЛЫ ДЛЯ РАСПРЕДЕЛЕНИЙ ВЕРОЯТНОСТИ
Ю.
Н. Кликушин
Омский государственный технический университет
Получена
14 ноября 2000 г.
Описаны
результаты исследований, связанных с представлением распределений вероятности
случайных сигналов в виде порядковых идентификационных шкал. Подобные шкалы
предназначены для использования в интеллектуальных системах измерения, контроля
и диагностики в качестве базы эталонных образов.
ВВЕДЕНИЕ
Качественный уровень интеллектуальных средств измерения, контроля и диагностики определяется, кроме всего прочего, их способностью принимать адекватные решения в условиях, когда для входной информации в базе знаний не находится, для формирования условия эквивалентности, соответствующего эталонного образа.
Традиционный подход в этом случае состоит в том, что неизвестному входному образу присваивается имя "ближайшего" эталона. При этом не учитываются вклады, вносимые в оценку понятия "ближайшего" расстояния остальных эталонов базы знаний.
Для обоснования подобной процедуры распознавания обычно ссылаются на количественные критерии оценки понятия "малости расстояния" между образами. Так, например, в теории измерений и прикладной статистике [1-3] в качестве такого критерия используется "правило 3-х сигм", в соответствии с которым, при суммировании двух составляющих погрешности измерения, выраженных своими среднеквадратическими отклонениями (СКО), "малой" считается та составляющая, СКО которой в 3 раза меньше, чем у другой составляющей. Применение подобных критериев в задачах распознавания образов ведет к "округлению" результатов и, как следствие, к ограничению разрешающей способности числом используемых эталонов.
Автором была разработана новая технология распознавания [4], позволяющая формировать такой результат, который учитывает влияние всех эталонов базы данных. Идея подобной технологии основана на применении порядковой шкалы эталонов. Шкала является универсальным и компактным средством отображения самого общего вида связи между эталонами, позволяющим совместить функции аналого-цифрового преобразования и интерполяции неизвестного образа.
Предположим,
что имеется две системы распознавания, содержащие одинаковое число, например k=4, эталонов. Пусть
в первой системе эталоны неупорядочены. В такой системе число различимых
градаций равно числу k эталонов, т.е. 4. Пусть во второй
системе эталоны организованы в виде порядковой шкалы и помечены номерами от 1
до 4. Каждому входному образу будут сопоставлены одновременно все четыре эталона. Однако порядок следования
эталонов может быть разным. Поэтому для системы распознавания с порядковой
шкалой эталонов число различимых градаций составит k!=4!=24. Таким
образом, выигрыш в разрешающей
способности для системы с упорядоченной базой эталонов составит (k-1)!. Совокупность
порядковых номеров эталонов можно рассматривать как своеобразный
"позиционный"
код (ПК) входного образа, число разрядов которого равно числу эталонов, причем
разряды имеют качественную характеристику в виде имен эталонов.
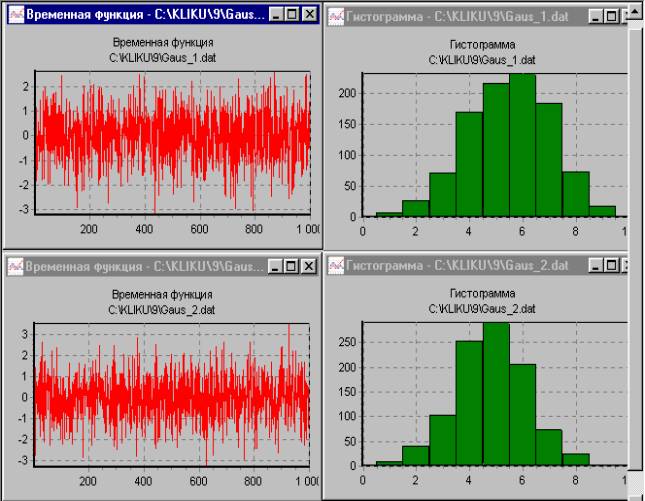
Результаты (табл.1) идентификации двух случайных сигналов (рис.1) иллюстрируют идею метода. Первые 3 и последние 2 разряда ПК сравниваемых сигналов совпадают. Отличия проявляются в 4 и 5 разрядах так, что ПК второго сигнала оказывается больше аналогичного ПК первого: ПК2>ПК1. Физический смысл подобного соотношения состоит в том, при одинаковой форме "ближайшего" распределения (НОРМ – нормальное), плотность вероятности второго сигнала более концентрирована.
Рис.1. Временные функции и гистограммы сравниваемых случайных сигналов
|
Имя файла сигнала |
GAUS_1.DAT |
Имя файла сигнала |
GAUS_2.DAT |
|
ПК |
Имя эталона |
ПК |
Имя эталона |
|
5 |
НОРМ |
5 |
НОРМ |
|
4 |
СИМП |
4 |
СИМП |
|
6 |
ЛАПЛ |
6 |
ЛАПЛ |
|
3 |
РАВН |
7 |
КОШИ |
|
7 |
КОШИ |
3 |
РАВН |
|
2 |
АРКС |
2 |
АРКС |
|
1 |
2МОД |
1 |
2МОД |
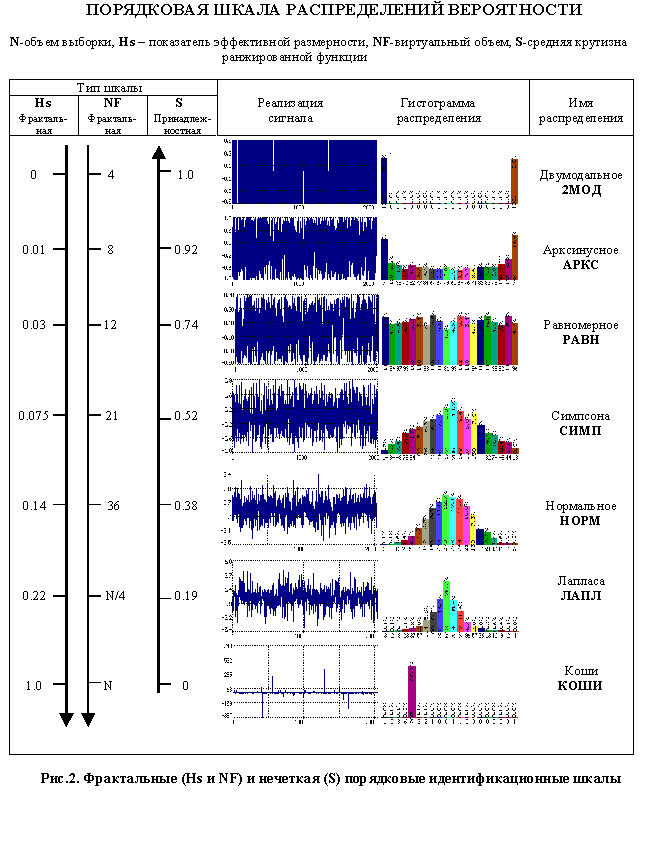
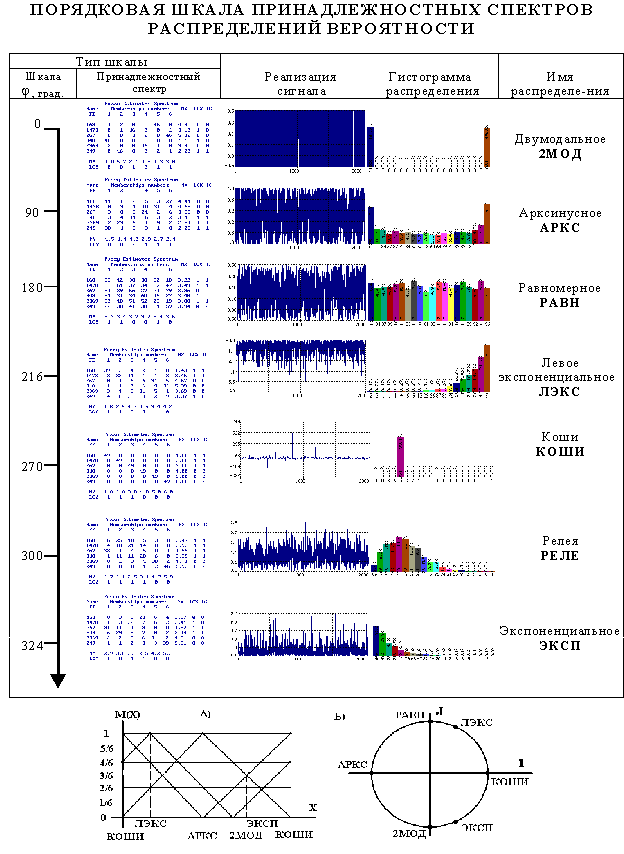
Рис.3. Порядковая шкала принадлежностных спектров распределений
вероятности
Чтобы реализовать указанный подход в распознавании образов, требуется иметь упорядоченные шкалы эталонов. Решение задачи создания подобных шкал было впервые дано в [5], где описаны соответствующие технологии, основанные на нечетких и фрактальных моделях представления сигналов. Оснвные результаты проведенных исследований в компактной и наглядной форме изложены в данной работе.
МОДЕЛИ И
АЛГОРИТМЫ ПОРЯДКОВЫХ ШКАЛ РАСПРЕДЕЛЕНИЙ ВЕРОЯТНОСТИ
Порядковые
шкалы распределений упорядочивают их форму по свойствам либо
концентрированности – размытости (рис.2), либо симметрии – асимметрии и концентрированности – размытости
одновременно (рис.3). В качестве числовых упорядочивающих коэффициентов были использованы
следующие параметры:
а)
показатель эффективной размерности Hs;
б)
виртуальный объем выборки NF;
в)
средняя крутизна нормированной ранжированной функции сигнала на центральном ее
участке S;
г) фазовый угол, определяющий положение максимумов функции принадлежности в спектре нечетких оценок центра распределения.
Первые
два показателя относятся к классу фрактальных моделей, два других – к классу
нечетких моделей представления входных сигналов.
Метод эффективной размерности (МЭР). Является прямым
аналогом метода Херста [6] во фрактальном анализе временных рядов наблюдений.
Однако, в отличие от последнего, моделью метода эффективной размерности служит
уравнение (1), определяющее отношение размаха сигнала (а не размаха
накопленного отклонения как в методе Херста) к его среднеквадратическому отклонению
от среднего:
![]() (1)
(1)
где: Аs, Нs – параметры зависимости – коэффициенты, которые требуется оценивать по
результатам измерения; N – текущий
объем выборки, последовательно сканируемый в диапазоне от 2 до Nmax и представляющий собой в данной
формуле независимую переменную. Информативным параметром в
(1) является
показатель Hs эффективной
размерности сигнала, оценивать который удобнее всего, используя логарифмическую
форму записи:
![]() (2)
(2)
в которой Hs определяет угол наклона прямой
линии, аппроксимирующей точки зависимости ![]() где
где ![]()
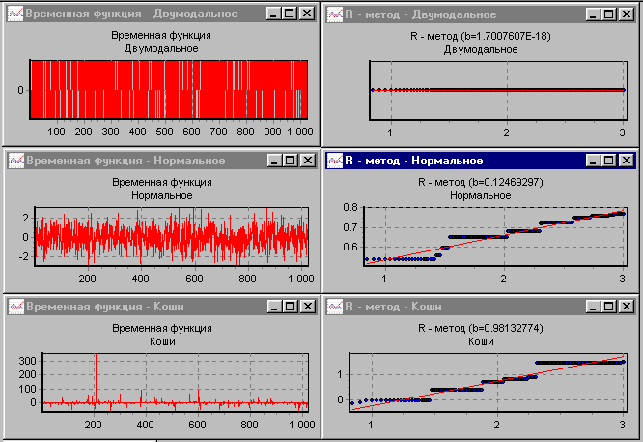
Рис.4. Типовые реализации сигналов с 2МОД, НОРМ и КОШИ распределениями и их
фрактальные функции в логарифмическом масштабе
На рис.4 представлены типовые реализации некоторых
стационарных случайных сигналов и их фрактальные функции (2). Угол наклона
регрессионной прямой, проведенной к фрактальной линии определяет оценку b показателя Hs эффективной размерности.
Проведенными исследованиями установлено, что численные значения показателя Hs зависят от вида распределения, меняясь от
0 у двумодального (2МОД), до 1 – у распределения Коши (КОШИ) (табл.2).
Таблица 2.
|
Параметры |
2МОД
|
АРКС |
РАВН |
СИМП |
НОРМ |
ЛАПЛ |
КОШИ |
|
Показатель
эфф.размерности, Hs |
0 |
0.01 |
0.03 |
0.075 |
0.14 |
0.22 |
1.0 |
|
Погрешность |
1 |
1 |
2 |
3 |
5 |
8 |
40 |
Представленные в табл.2 оценки показателя Hs эффективной размерности получены усреднением 1000 реализаций объема Nmax=2000 для каждого из симметричных распределений. Эти оценки использованы в дальнейшем в качестве "оцифрованных отметок" фрактальной порядковой шкалы распределений. Оценки погрешностей "оцифрованных отметок" даны в приведенной (к max Hs=1) форме и рассчитаны через среднеквадратическое отклонение как случайные погрешности среднего для уровня доверительной вероятности 0.95:
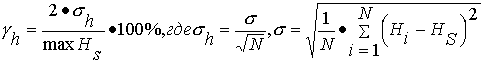 .
.
Знание показателя
Hs эффективной размерности позволяет определить
стационарную размерность сигнала в виде: Ds=2-Hs. Для показанных на рис.4 сигналов, стационарная размерность,
соответственно, составит: Ds(2МОД)=2,
Ds(НОРМ)=1.88 и Ds(КОШИ)=1. Топологическая размерность плоскости совпадает со стационарной
размерностью сигнала с 2МОД распределением. С другой стороны, стационарная
размерность случайного сигнала с КОШИ распределением совпадает с топологической
размерностью линии (Dt=1).
Между этими двумя крайними случаями целочисленной размерности лежат сигналы с
нецелочисленной стационарной размерностью, например, сигнал с НОРМ
распределением (Ds(НОРМ)=1.86-1.88).
Физическая интерпретация понятия стационарной размерности связана с понятием
хаотичности (изменчивости) случайных сигналов – сигнал большей размерности имеет более высокую
хаотичность.
Метод виртуальных объемов
(МВО). Использует, как и
предыдущий метод, отношение размаха сигнала к его СКО. Математическая модель
МВО:
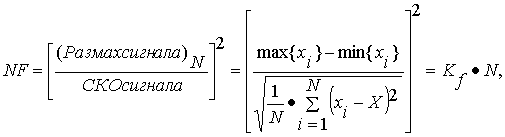 (3)
(3)
трактует
обработку значений {X} сигнала
как преобразование количества информации объема N на входе системы распознавания в количество информации объема
NF на выходе.
При постоянном объеме N входных данных свойства сигнала полностью определяются фрактальным
коэффициентом передачи Kf. Если ввести предположение о динамическом
характере процесса преобразования, то модель (3) можно детализировать, описав
ее, например, уравнением апериодического типа
[7]:
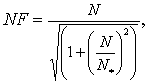 (4)
(4)
где:
единственный модельный параметр N* характеризует
такой объем выборки, при котором фрактальный коэффициент передачи равен
»0.707 от максимального значения. Физический смысл формулы
(4) заключается в
том, что оценка свойств сигнала с помощью виртуального объема NF, зависит от времени наблюдения (N) и типа процесса (N*).
Анализ асимптотического поведения модели
(4)
позволяет предсказать свойства граничных процессов. Например:
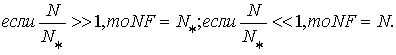
Первое условие объединяет "малоинерционные" процессы, свойства которых можно оценить, выбрав достаточно большое время наблюдения. У таких процессов экстремальные значения появляются часто (многократно за время наблюдения). Фрактальный коэффициент передачи подобных процессов меньше 1, что соответствует модели электрической цепи с потерями. Примером подобного сигнала может служить, показанный на рис.4, сигнал с 2МОД распределением.
|
|
|
|
а) |
б) |
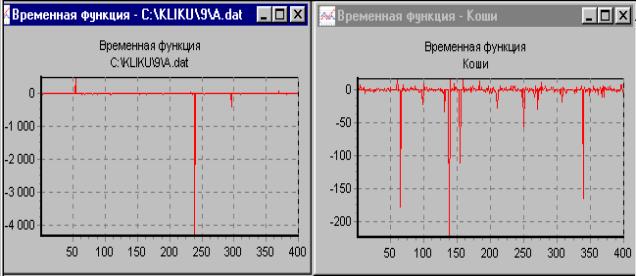
Рис.5. Две реализации сигнала с КОШИ распределением и различными значениями
фрактального коэффициента передачи: а) Kf=1.22; б) Kf=0.44
Второе условие характерно для весьма
"инерционных"
процессов, у которых собственное критическое время (N*) стремится к бесконечности. Фрактальный коэффициент передачи подобных
процессов равен 1, что соответствует модели электрической цепи без потерь.
В связи с анализом граничных значений
NF возникает интересный вопрос:
существуют ли такие условия (или процессы), для которых фрактальный коэффициент
передачи больше 1? В эксперименте с генератором случайного сигнала, имеющего
КОШИ распределение, было зафиксировано примерно (15-20)% реализаций, для
которых наблюдался подобный эффект увеличения количества информации на выходе
системы по сравнению с количеством информации на входе (NF>N).
Примеры сигналов, имеющих фрактальные коэффициенты передачи как
меньше, так и больше 1, представлены на рис.5.
Метод средней крутизны
ранжированной функции.
Является алгоритмически наиболее простым методом шкалирования (рис.2)
распределений вероятности. Суть его сводится к следующему
[4].
-
Исследуемая выборка ранжируется по возрастанию.
-
Из ранжированной функции путем равномерной дискретизации выбирается 9 значений, причем пятое по счету значение должно совпадать с медианой исследуемой выборки.
-
Вычисляется модельный параметр, определяемый как:
где:
C(I) – i-ое значение
ранжированной функции исследуемой выборки. Численные значения параметра S отображают симметричные
распределения, как указано в табл.3.
Примерный вид ранжированных функций некоторых из
симметричных распределений представлен на рис.6. Вид этих функций не зависит от
параметров сдвига и масштаба, но крутизна на центральном участке плавно
увеличивается в направлении от КОШИ к 2МОД распределению.
|
Параметры |
2МОД
|
АРКС |
РАВН |
СИМП |
НОРМ |
ЛАПЛ |
КОШИ |
|
Крутизна
ранжированной функции S |
100 |
92 |
74 |
52 |
38 |
19 |
1.0 |
|
Погрешность gS, % |
0.1 |
0.2 |
0.4 |
0.6 |
0.8 |
0.6 |
0.3 |
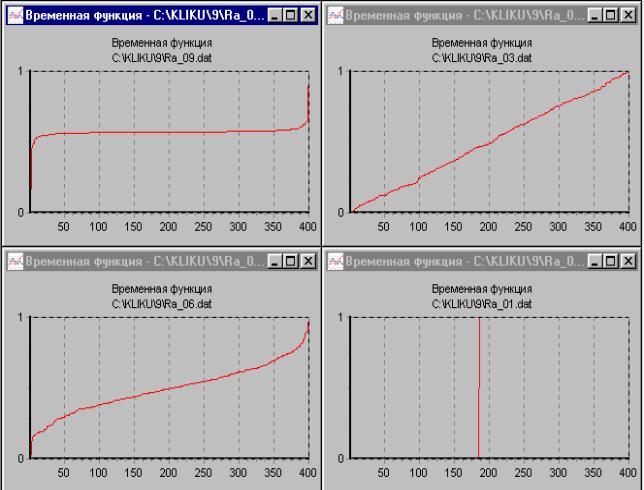
Рис.6. Вид ранжированных функций реализаций с КОШИ, НОРМ, РАВН и 2МОД распределениями
Простота реализации и статистическая устойчивость
метода позволяют рекомендовать его для решения задач идентификации вместо
устаревших технологий типа проверки статистических гипотез и методов,
основанных на анализе моментов распределений.
Метод принадлежностных
спектров. Идея и суть
метода подробно изложены в работах [4,5]. Шкала (рис.3) метода представляет
собой окружность единичного радиуса в комплексной плоскости. Геометрическим
местом симметричных выпуклых распределений служит положительное направление оси
абсцисс, а симметричных вогнутых – отрицательное. Распределения РАВН и 2МОД не
имеют ни выпуклости, ни вогнутости, поэтому их точки расположены на мнимой оси.
В точках пересечения осей координат с окружностью расположены
"канонические"
распределения (2МОД, АРКС, РАВН и КОШИ). Остальные точки окружности являются
геометрическим местом различных асимметричных распределений. Информативным
параметром метода служит угловое положение вектора формы, который отображает
положение максимумов функции принадлежности в спектре нечетких оценок центра
распределения.
Таблица 4.
Вероятности
принятия решений о выборе одного из 5 эталонных распределений, если на входе
распознавалось одно из 10 распределений
|
№ |
Имя |
2МОД | АРКС | ЛЭКС | КОШИ | ЭКСП |
| 1 | 2МОД | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | АРКС | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 |
| 3 | ЛЭКС | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 |
| 4 | КОШИ | 0.01 | 0.01 | 0.00 | 0.95 | 0.04 |
| 5 | ЭКСП | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 |
| 6 | РЕЛЕ | 0.00 | 0.00 | 0.00 | 0.64 | 0.36 |
| 7 | РАВН | 0.16 | 0.13 | 0.12 | 0.45 | 0.15 |
| 8 | СИМП | 0.00 | 0.00 | 0.02 | 0.96 | 0.03 |
| 9 | НОРМ | 0.00 | 0.00 | 0.05 | 0.88 | 0.08 |
| 10 | ЛАПЛ | 0.00 | 0.00 | 0.03 | 0.91 | 0.07 |
В табл.4 представлены результаты распознавания
случайных сигналов с различными распределениями методом принадлежностных
спектров с пятью эталонами: 2МОД – АРКС – ЛЭКС – КОШИ – ЭКСП. Здесь ЛЭКС –
левоасимметричное, а ЭКСП – правоасимметричное распределения. В эксперименте
тестировалось 10 распределений, представленное каждое 200 реализациями объема
N=1000.
Первые пять распределений совпадают с эталонами и
вероятность их правильного распознавания составляет не менее 95%. Шестое
распределение (Релея) относится к классу асимметричных. В рамках принятых
эталонов оно раскладывается на две компоненты КОШИ и ЭКСП в пропорциональности
примерно 2 к 1. Седьмое (РАВН) распределение оказалось размытым по всем
эталонным компонентам с заметным преобладанием КОШИ. Остальные симметричные
выпуклые распределения (СИМП, НОРМ и ЛАПЛ) маскируются симметричным выпуклым
эталонным распределением КОШИ, что находится в полном соответствии с,
рассмотренной в [4], круговой моделью шкалы.
Методологическое значение метода обусловлено
возможностью создания алгебры образов распределений – формального логического
аппарата для описания операций с подобными сложными объектами.
ЗАКЛЮЧЕНИЕ
Если предположить, что
"форма распределения"
является непрерывной величиной, то порядковые шкалы можно считать
аналого-цифровыми преобразователями (АЦП). Такие АЦП относятся к классу
параллельных, поскольку неизвестный входной образ сравнивается сразу с полной
шкалой эталонов. Сами эталоны в этом случае играют роль
"оцифрованных отметок"
шкалы. Следовательно, как и в обычных измерительных приборах физических величин,
достоверность преобразования будет зависеть, в первую очередь, от качества
используемой шкалы эталонов. При этом положение
"оцифрованных отметок"
определяет систематическую, а размытость отметки – случайную, составляющие
погрешности шкалы.
Указанные особенности позволяют
сформировать единую методологическую базу описания процессов распознавания и
измерения и, соответственно, использовать стандартный, узаконенный
понятийный аппарат метрологии при
решении задач распознавания образов.
ЛИТЕРАТУРА
-
Фрумкин В.Д., Рубичев Н.А. Теория вероятности и статистика в метрологии и измерительной технике. –М.: Машиностроение, 1987.
-
Грановский В.А., Сирая Т.Н. Методы обработки экспериментальных данных при ихмерениях. – Л.: Энергоатомиздат, 1990.
-
Тойберт П. Оценка точности результатов измерений: Пер. с нем. – М.: Энергоатомиздат, 1988.
-
Кликушин Ю.Н. Представление случайных сигналов с помощью принадлежностных спектров. – Интернет-публикация, М.: Журнал Радиоэлектроники, № 2, 2000.
-
Кликушин Ю.Н. Идентификационные шкалы: теория, технологии, системы//Рукоп.диссерт.на соиск. ученой степени докт.техн.наук – Омск, Омский государственный технический университет, 2000.
-
Кликушин Ю.Н. Фрактальная шкала для измерения распределений вероятности. – Интернет-публикация, М.: Журнал Радиоэлектроники, № 3, 2000.
Автор: Кликушин Юрий
Николаевич, профессор кафедры "Информационно-измерительная техника" Омского
государственного технического университета, к.т.н.
E-mail:
lab308@omgtu.omskelecom.ru