ПРОСТРАНСТВЕННЫЕ ФУНКЦИИ НЕОПРЕДЕЛЕННОСТИ ДЛЯ АЛГОРИТМ ОПТИМАЛЬНОЙ ОЦЕНКИ СТОХАСТИЧЕСКИХ ХАРАКТЕРИСТИК ПОВЕРХНОСТИ

В. К. Волосюк,  А. В. Ксендзук

Харьковский Национальный Аэрокосмический Университет им Н.Е. Жуковского

Получена 15 ноября 2000 г.

Рассмотрены пространственные функции неопределенности для  стандартного оптимального алгоритма обработки сигналов в радарах с синтезированием апертуры (РСА)  и для синтезированного алгоритма оптимальной оценки стохастических параметров поверхности. Предложенный алгоритм получен в предположении нормальности и коррелированности сигналов отраженных от поверхности полей. Построены пространственные функции неопределенности, характеризующие разрешающую способность системы, вероятность обнаружения/распознавания малоразмерных целей в зависимости от отношения сигнал/шум в системе.

Рассмотрим задачи оптимальной оценки электрофизических параметров поверхности и их статистических характеристик  для стохастических моделей поверхности. В отличие от функционально-детерминированных  моделей поверхности [1], принимаемые к рассмотрению содержат случайные параметры (флуктуации амплитуды и фазы)

В рамках метода максимального правдоподобия оптимальную оценку параметра  (где - вектор электрофизических параметров поверхности) находим по максимуму функции правдоподобия: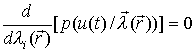 для удобства воспользуемся монотонным преобразованием функции правдоподобия  .

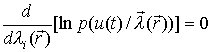Входной процесс является случайным нормальным процессом, состоящим из суммы аддитивного (нормального дельта-коррелированного процесса) и нормального коррелированного процесса (при представлении поверхности множеством независимых элементарных отражателей  в силу центральной предельной теоремы совокупность принятых сигналов будет иметь нормальное распределение). Запишем плотность вероятности такого сигнала:

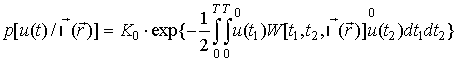,                                   (1)

где - центрированное значение входного процесса;  - функция, обратная корреляционной функции .

Сигнал на входе приемной антенны представим как сумму (в пределе переходящую в интеграл)  сигналов, принятых от элементарных отражателей:

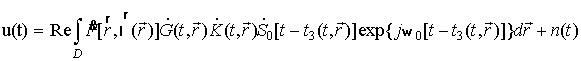,    (2)

где  - комплексный коэффициент отражения поверхности (является случайной величиной для стохастических моделей параметров поверхности);  - коэффициент, включающий детерминированные параметры, влияющие на распространение сигнала (диаграммы направленности антенн, параметры атмосферы);  - коэффициент, включающие в себя случайные параметры, валяющие на распространение сигнала (турбулентность атмосферы   и другие случайные факторы); - огибающая излучаемого сигнала (в общем случае комплексная).

Обычно среднее  принимаемого сигнала равно нулю (при малом изменении коэффициентов  и , -модель крупномасштабной поверхности, - за счет высокочастотного сомножителя; для модели мелкомасштабной поверхности - в силу того, что ). В реальных системах при наличии пассивных помех аддитивный шум    также имеет нулевое среднее, на основании вышесказанного далее предполагается центрированность входного процесса

Коэффициент  в общем случае является бесконечно большим, (в дискретном случае , переход к континуальному случаю осуществляется  при ). Однако в  практических условиях функционирования приходится сравнивать условные плотности вероятности, либо оперировать с производной данного коэффициента. Если переходить к пределу после сравнения или дифференцирования, результат будет в общем случае сходиться.

Так, например, для вариационной производной по параметру  (вариационной, так как  оцениваемые параметры являются функциями координат), [2]:

.

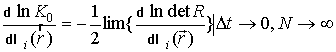
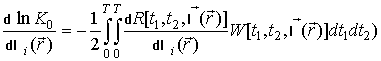Как было упомянуто ранее, уравнение для отыскания оптимальной оценки в рамках метода максимального правдоподобия находится из следующего уравнения:

,

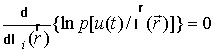где 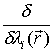 - знак вариационной (функциональной) производной; при подстановке (1) получим:

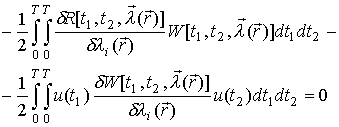.                                                                 (2)

Выражение для обратно корреляционной функции (декоррелирующего оператора) в дискретном случае находится путем обращения корреляционной матрицы   (), при предельном переходе данное выражение преобразуется к интегральному уравнению обращения:

,                                                                      (3)

где - дельта-функция (функция Дирака).

Из (3) нетрудно найти выражение для вариационной производной декоррелирующего оператора по параметру :

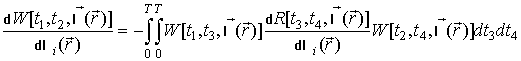.                    (4)

Подставим данное выражение в (2) и преобразуем его, используя тождество

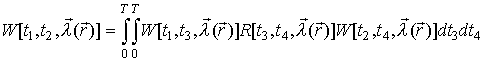,                             (5)

в результате получим следующее уравнение:

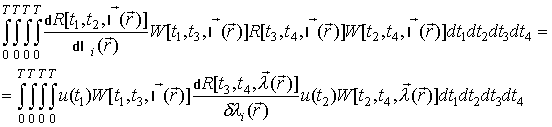.            (6)

Корреляционная функция входного процесса : , где , , тогда если случайные процессы  и  статистически независимы, причем среднее аддитивного шума равно нулю (), то , получим следующее выражение для корреляционной функции:

где - корреляционная функция аддитивного шума, в дальнейшем полагаем, что .

Используя равенство , где - удельная ЭПР поверхности, усредненная по ансамблю реализаций (для эргодических процессов это эквивалентно усреднению по времени), - дельта- функция, получим окончательное выражение для корреляционной функции принимаемого сигнала.

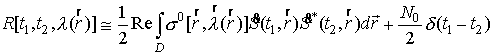.                           (7)

Тогда выражение для вариационной производной корреляционной функции будет следующим:

,                                                 (8)

при подстановке (7) и (8) в (6) получим:

.

После несложных преобразований (учитывая, что равенство комплексных величин более сильно, чем равенство их реальных частей), данное уравнение приводится к виду

,

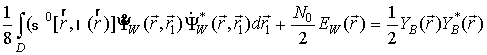или

,                                                     (9)

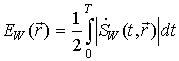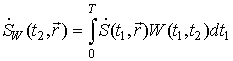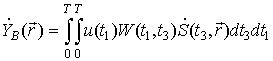где приняты следующие обозначения: - пространственная корреляционная функция неопределенности при обработке с декорреляцией, ;  - та же функция, но сопряженная ; - энергия сигнала  ;  сигнал при обработке с декорреляцией; - оптимальный выходной эффект системы  (достаточная статистика), ;  - сопряженный выходной эффект системы .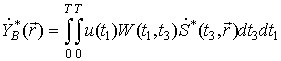

В соответствии с данным уравнением оптимальный выходной эффект системы (правая часть уравнения) - это изображение поверхности, сглаженное квадратом модуля пространственной корреляционной функции .

Для сравнения предложенного алгоритма со стандартным оптимальным были построены пространственные функции неопределенности для монохроматического излучаемого сигнала при различном  отношения сигнал/шум (изображены ниже на рис.1-рис.4).

Рис.1. Пространственная функция неопределенности для стандартной оптимальной обработки.

Рис.2. Пространственные функции неопределенности для предложенного алгоритма, отношение сигнал/шум =  5.

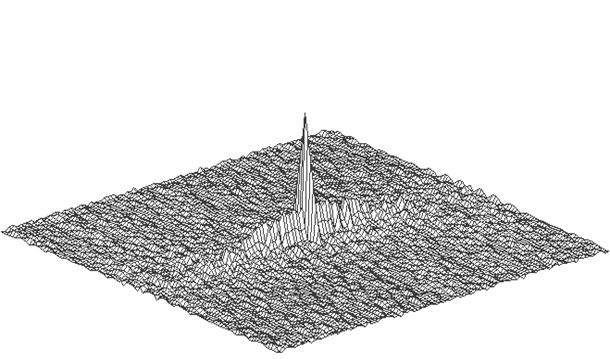
Рис.3. Пространственные функции неопределенности для предложенного алгоритма, отношение сигнал/шум =  20.

Рис.4. Пространственные функции неопределенности для предложенного алгоритма, отношение сигнал/шум =  50.

Как видно из приведенных построений, пространственная функция неопределенности, которая фактически определяет такие важные параметры  системы как разрешающая способность, вероятность обнаружения малоразмерных целей, вероятность правильного распознавания объектов,  сужается при использовании предложенного алгоритма (коэффициент сжатия пространственной функции неопределенности и динамическая/флуктуационная ошибки оценки параметров поверхности были рассмотрены в [3]). Результаты позволяет рекомендовать использование данного алгоритма обработки при построении высокоточных систем дистанционного зондирования.

Литература

1. Волосюк В.К., Кравченко В.Ф. Оценка электродинамических параметров поверхности на основе их моделей. – Изв. вузов. Сер. Радиоэлектроника,. 1991, т.34, № 9, с. 4-88.

2. Бакут, Большаков и др. Вопросы статистической теории радиолокации. – Москва : Советское радио, 1963, т.1.

3. Ксендзук А.В .Улучшение радиоизображений РСА применением алгоритмов декорреляции. – Вестник ХГПУ, 2000, № 80, с. 12-14

Авторы:

Д.т.н. проф. Волосюк В.К. , Ксендзук А.В.
Харьковский Национальный Аэрокосмический Университет им Н.Е. Жуковского, "ХАИ", e-mail kvm@systud.msk.su