|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 11, 2002 |
|
ВЛИЯНИЕ АКУСТИЧЕСКОЙ НЕЛИНЕЙНОСТИ НА СВЕРХВЫСОКОЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ПОВЕРХНОСТНЫХ АКУСТИЧЕСКИХ ВОЛН
Д.С.Сучков1), С.Г.Сучков2); e-mail: suchkov@ssu.runnet.ru
1) Саратовский центр научно-технической информации,
2) Саратовский государственный университет
Получена 5 ноября 2002 г.
На распространение поверхностных акустических волн в диапазоне частот около10 ГГц существенное влияние оказывает акустическая нелинейность тензора деформаций, приводящая к дисперсии и росту затухания. Расчеты, иллюстрирующие это явление, проведены для кристаллов кварца и ниобата лития.
В последнее время частотный диапазон разрабатываемых устройств на поверхностных акустических волнах (ПАВ), в частности для систем мобильной связи, продвинулся в область частот свыше 5 ГГц [1,2]. Вместе с тем интерес проявляется к использованию ПАВ в мощных выходных каскадах антенных устройств [3]. При этом расчет характеристик распространения ПАВ в кристаллах, необходимый при создании таких приборов, практически всегда использует линейное приближение, в котором вместо полного тензора деформации
берется только линейная по упругим смещениям ui часть (индексы принимают значения 1,2,3 и по повторяющимся индексам производится суммирование). Однако для ПАВ, распространяющихся вблизи поверхности раздела сред, имеющих сильно отличающиеся акустические свойства, значения производных по нормали к поверхности могут быть не малыми, и их произведение может быть сравнимым с линейными членами (1) [4]. Наиболее существенного влияния нелинейности, очевидно, можно ожидать при решении задачи о распространении ПАВ на границе кристалл-вакуум. Кроме того, поток энергии ПАВ сконцентрирован в тонком приповерхностном слое толщиной порядка длины волны, поэтому плотность акустической энергии возрастает пропорционально частоте и для использования ПАВ на частотах 10 ГГц и выше, где длина волны составляет доли микрона, представляется необходимым оценить границу применимости линейного приближения.
Строго говоря, при решении задачи о поверхностной волне полный тензор деформаций (1) нужно использовать как при решении уравнений Кристоффеля
где сijlm – тензор модулей упругости, elij.- тензор пьезомодулей, j - электрический потенциал, так и при подчинении решений (2)
граничному условию для тензора упругих напряжений ![]() на свободной поверхности (перпендикулярной
оси z)
на свободной поверхности (перпендикулярной
оси z)
В задаче о поверхностной волне уравнения (2) определяют только связь поперечных компонент волнового вектора (декрементов затухания вглубь кристалла) с модулем волнового вектора ПАВ ks=2p /ls, а также соотношения компонент смещений (поляризационные коэффициенты) в каждой из четырех парциальных мод колебаний, то есть определяет некоторые характеристики пространственной структуры ПАВ. Полностью же пространственная структура ПАВ определяется граничными условиями, из которых находится волновой вектор ПАВ ks и устанавливаются соотношения между амплитудами четырех мод колебаний [4,5]. Поэтому учет нелинейности в задаче о ПАВ можно провести только в граничном условии (3), пересчитывая при этом декременты затухания и поляризационные коэффициенты из (2) с учетом нелинейных изменений волнового вектора поверхностной волны ks.
Рассмотрим граничное
условие (3) для тензора упругих напряжений ![]() на свободной границе пьезокристаллического
полупространства, перпендикулярной к оси z. Возьмем фазовую зависимость электрического
потенциала и упругих смещений ПАВ в виде
на свободной границе пьезокристаллического
полупространства, перпендикулярной к оси z. Возьмем фазовую зависимость электрического
потенциала и упругих смещений ПАВ в виде
![]() ,
,
тогда с учетом (1) граничное условие (2) можно записать в виде:
 .
(3)
.
(3)
Таким образом, из (3) видно, что влияние нелинейности в граничном условии увеличивается с ростом частоты и зависит от структуры волны, определяющей отношение квадрата полной амплитуды смещения к компоненте смещения um .Выражение в скобках можно рассматривать как множитель, изменяющий модуль упругости. Тогда эффективный модуль упругости среды становится комплексным, что приводит к затуханию ПАВ. Очевидно, ПАВ теряет энергию вследствие генерации высших гармоник частоты.
Расчет линейных характеристик
распространения ПАВ – фазовой скорости V и затухания A – с учетом нелинейности в граничных условиях проведем для
пьезокристаллов инвариантным методом [5]. Для этого в нулевом приближении (без
учета нелинейности в граничном условии) рассчитаем фазовые характеристики ПАВ V(0) и A(0),
а также 4 парциальных потенциала ![]() и 12 компонент упругих смещений
и 12 компонент упругих смещений ![]() (индекс
i=
(индекс
i=![]() 1,2,3 нумерует компоненты вектора
смещения, а n=1,2,3,4
– моды колебаний). При этом потенциал первой моды считаем равным одному вольту.
Затем с полученными амплитудами упругих смещений
1,2,3 нумерует компоненты вектора
смещения, а n=1,2,3,4
– моды колебаний). При этом потенциал первой моды считаем равным одному вольту.
Затем с полученными амплитудами упругих смещений ![]() вычислим первое
приближение, используя нелинейное граничное условие (3) в виде:
вычислим первое
приближение, используя нелинейное граничное условие (3) в виде:
 (4)
(4)
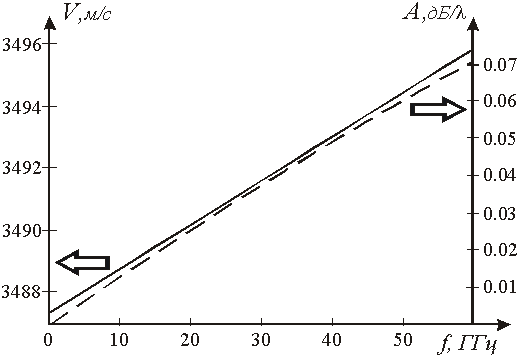
Рис.1. Частотная зависимость фазовой скорости V (сплошная линия)
и нелинейного затухания A (штриховая линия) ПАВ в кристалле LiNbO3 YX-среза.
Полученные значения фазовых характеристик V(1)
, A(1) и упругих смещений ![]() могут далее использоваться для получения высших приближений,
однако в этом нет необходимости ввиду незначительного отличия второго
приближения от первого. На рис. 1 приведены результаты расчета (в первом
приближении) фазовой скорости V и затухания A ПАВ для кристалла ниобата лития Y-среза
в направлении оси Х.
могут далее использоваться для получения высших приближений,
однако в этом нет необходимости ввиду незначительного отличия второго
приближения от первого. На рис. 1 приведены результаты расчета (в первом
приближении) фазовой скорости V и затухания A ПАВ для кристалла ниобата лития Y-среза
в направлении оси Х.
При заданном потенциале
первой моды ![]() =1(В)
линейная (вдоль фронта волны) плотность потока мощности ПАВ на частоте f = 1 ГГц составляет PL=8.67 (Вт/м) в ниобате лития и PL=26.9 (Вт/м) для кварца ST-среза.
Если принять ширину акустического потока в устройстве обработки сигнала W=100l, то мощность сигнала при выбранной нормировке на любых
частотах составит PС =3 мВт для
ниобата лития и PС =8.5 мВт для
кварца. Как показывают результаты, представленные на рис.1, на высоких
частотах уже при такой сравнительно малой мощности влияние нелинейности на
скорость и затухание ПАВ весьма существенно. Поэтому определение частотной
границы fG линейного приближения в
зависимости от мощности сигнала PС
представляет практический интерес для разработки устройстве на ПАВ в диапазоне
частот 10 ГГц и выше.
=1(В)
линейная (вдоль фронта волны) плотность потока мощности ПАВ на частоте f = 1 ГГц составляет PL=8.67 (Вт/м) в ниобате лития и PL=26.9 (Вт/м) для кварца ST-среза.
Если принять ширину акустического потока в устройстве обработки сигнала W=100l, то мощность сигнала при выбранной нормировке на любых
частотах составит PС =3 мВт для
ниобата лития и PС =8.5 мВт для
кварца. Как показывают результаты, представленные на рис.1, на высоких
частотах уже при такой сравнительно малой мощности влияние нелинейности на
скорость и затухание ПАВ весьма существенно. Поэтому определение частотной
границы fG линейного приближения в
зависимости от мощности сигнала PС
представляет практический интерес для разработки устройстве на ПАВ в диапазоне
частот 10 ГГц и выше.
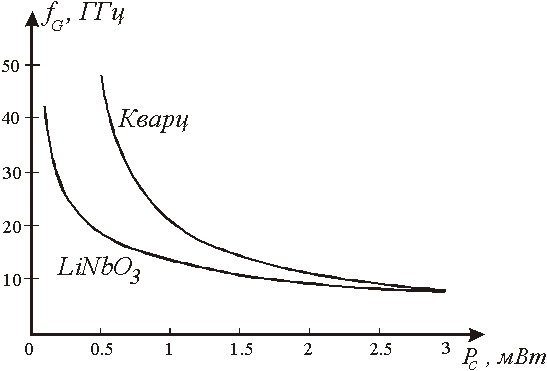
Рис.2. Зависимость частотной границы линейного приближения fG
от мощности сигнала РС для ST-X-среза кварца и YХ-среза ниобата лития.
Будем считать граничными частотами линейного приближения такие значения частоты fG, при которых расчетная величина нелинейных потерь ПАВ A=0.01(дБ/l). Определенные таким условием зависимости fG(PC) для кварца и ниобата лития приведены на рис.2.
Приведенные результаты показывают, что акустическая нелинейность в ниобате лития выражена значительно сильнее, чем в кварце. А поскольку на частотах 2-10 ГГц вследствие малого затухания ПАВ применяют именно ниобат лития, то для исключения нелинейных искажений мощность ПАВ не должна превышать долей милливатта.
Нелинейное затухание на сверхвысоких частотах определяется линейной по частоте мнимой добавкой в эффективном тензоре упругости (3) так же, как и вязкостное затухание, определяемое тензором вязкости hijlm в комплексном тензоре упругости [6]
![]() .
.
Поэтому при измерениях затухания ПАВ на сверхвысоких частотах эти факторы приводят к одинаковой квадратичной зависимости потерь на распространение от частоты и для их разделения необходимо проводить описанный выше нелинейный расчет.
Поскольку нелинейная поправка в граничных условиях зависит от структуры ПАВ, то некоторого ослабления влияния нелинейности на СВЧ характеристики ПАВ можно добиться выбором кристаллических срезов и направлений. Кроме того, для уменьшения неоднородности смещений ПАВ вблизи границы раздела сред видимо, целесообразно использовать слоистые структуры. В этом смысле перспективным направлением можно считать применение алмазных пленок [2].
СПИСОК ЛИТЕРАТУРЫ
1. S.Lehtonen, M.T.Honkanen, V.P.Plessky, J.Turunen, M.M.Salomaa. Experimental Study of SAW Resonators Operating at 7.5 GHz. ABSTRACTS 2001 IEEE International Ultrasonics Symposium, October 7-10, 2001, Atlanta, USA, p. 58.
2. H.Nakahata, A.Hachigo, K. Itakura, S.Shikata. Fabrication of High Frequency SAW Filters up to 10 GHz using Sio2/ZnO/Diamond Structure. ABSTRACTS 2000 IEEE International Ultrasonics Symposium, October 22-25, 2000, San Juan, Puerto Rico, p. 77.
3. O.Nakagawara, M.Saeki, N.Tsubaki . High Power Durable SAW Antenna Duplexer for W-CDMA with Epitaxially Grown Aluminium Electrodes. ABSTRACTS 2002 IEEE International Ultrasonics Symposium, October 8-11, 2002, Munich, Germany, p. 150.
4. Дж. Фарнел. Свойства упругих поверхностных волн. В кн. Физическая акустика. Принципы и методы. (под ред. У.Мэзона и Р.Терстона), т.VI, c.137. М.:-Изд. «МИР», 1973.
5. Казачкова Т.И., Лазерсон А.Г., Сучков С.Г. Численный анализ распространения поверхностных акустических волн в пьезокристаллах//Электронная техника.-сер.1, Электроника СВЧ.-1979.-вып.6.- С. 7-12.
6. Р.Терстон. Распространение волн в жидкостях и твердых телах. В кн. Физическая акустика (под ред. У.Мэзона), т.1, часть А., с.13. М.:-Изд. «МИР», 1966.
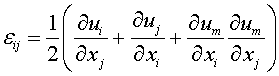 (1)
(1)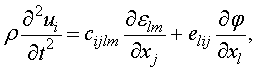 (2)
(2) (3)
(3)