Эффективность передающей многоэлементной антенны в системах мобильной связи
Г. В. Серебряков
Научно - Исследовательский институт Прикладной математики и кибернетики Нижегородского госуниверситета
Получена 21 октября 2009 г.
Одним из перспективных способов повышения качества передачи информации в современных системах беспроводной связи в сложных условиях распространения является использование многоэлементных антенных решеток на базовых станциях. В настоящей сообщении предлагается вариант передающей адаптивной антенны, максимизирующей отношение сигнал-шум в точке приема и одновременно минимизирующей мощность передачи в направлениях на других пользователей.
Ключевые слова – многоэлементная передающая антенная решетка, пилот сигнал.
В настоящее время многоэлементные антенные решетки (АР) находят все большее применение в системах мобильной связи [1,2]. Использование АР позволяет повысить пропускную способность благодаря повышению отношения сигнал-шум (ОСШ) в точке приема и подавлению внешних помех. Анализу эффективности приемных интеллектуальных антенн посвящено достаточно большое число работ (см., например [1-4]). В тоже время, представляется перспективным использование АР для передачи. Теоретически, выигрыш в ОСШ при использовании N-элементной АР достигает N раз. Однако, в реальных системах мобильной связи в силу различных ошибок этот выигрыш будет меньше. В частности, причинами уменьшения ОСШ могут быть фазовое рассогласование в силу неточного оценивания канала, влияние внешних помех и тд. Для преодоления проблемы фазового рассогласования в современных системах связи используется т.н. пилот сигнал, позволяющий, в частности, оценить канал распространения с целью последующего когерентного детектирования полезного сигнала. В настоящее время, наиболее типичным, является использование одного общего пилот сигнала для обслуживания всех пользователей в соте одновременно. В системах третьего поколения предусмотрено использование индивидуальных пилот сигналов для каждого полезного сигнала независимо. В настоящем сообщении исследована предложен вариант передающей АР, используемой для повышения ОСШ в двух случаях: с общим пилот сигналом, и пилот сигналом для каждого полезного сигнала.
Предположим, что базовая станция связана
с М пользователями в соте. Пусть ![]() - передаваемый полезный сигнал,
мощность и передающий весовой вектор m-ого пользователя (m=1,…,M). Соответственно,
- передаваемый полезный сигнал,
мощность и передающий весовой вектор m-ого пользователя (m=1,…,M). Соответственно, ![]() - передаваемый пилот
сигнал, его мощность и весовой вектор. Вектор передаваемого сигнала
- передаваемый пилот
сигнал, его мощность и весовой вектор. Вектор передаваемого сигнала ![]() с
базовой станции может быть записан как
с
базовой станции может быть записан как
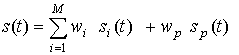 (1)
(1)
для случая с общим пилот-сигналом, и
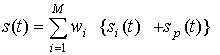 (2)
(2)
для
случая с индивидуальным для каждого полезного сигнала пилотом. Заметим, что в
случае использования общего пилот сигнала пилот луч должен быть достаточно
широким, чтобы покрывать всех пользователей. При использовании индивидуального
пилот сигнала, пространственный сектор передаваемого пилот сигнала должен
совпадать с лучом соответствующего полезного сигнала. Мы полагаем, что ![]() известен заранее. Сначала
рассмотрим случай общего пилот сигнала как более сложный. Основная проблема при
использовании передающих антенных решеток – это выбор весового вектора для каждого
передаваемого сигнала
известен заранее. Сначала
рассмотрим случай общего пилот сигнала как более сложный. Основная проблема при
использовании передающих антенных решеток – это выбор весового вектора для каждого
передаваемого сигнала ![]() в (1)-(2), обеспечивающего максимальное ОСШ в
точке приема с одной стороны, и минимальную мощность в направлениях на других
пользователей с другой. Принимаемый сигнал с базовой станции на m-пользователе может быть
записан в виде
в (1)-(2), обеспечивающего максимальное ОСШ в
точке приема с одной стороны, и минимальную мощность в направлениях на других
пользователей с другой. Принимаемый сигнал с базовой станции на m-пользователе может быть
записан в виде
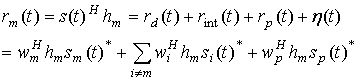
где
![]() – компоненты,
соответственно, полезного сигнала, внешних помех (сигналов от других
пользователей), пилот сигнала, собственного шума канала,
– компоненты,
соответственно, полезного сигнала, внешних помех (сигналов от других
пользователей), пилот сигнала, собственного шума канала, ![]() – вектор отклика канала
от базовой станции к m-пользователю с ковариационной матрицей
– вектор отклика канала
от базовой станции к m-пользователю с ковариационной матрицей ![]() , H – знак эрмитова сопряжения.
Мощность
, H – знак эрмитова сопряжения.
Мощность ![]() принимаемого сигнала
принимаемого сигнала ![]() записывается как
записывается как
![]()
Необходимо
учитывать, что благодаря разным весовым векторам полезного ![]() и пилот
и пилот ![]() сигналов, существует
фазовое рассогласование, которое приводит к тому, что не вся полная мощность
полезного сигнала
сигналов, существует
фазовое рассогласование, которое приводит к тому, что не вся полная мощность
полезного сигнала ![]() вносит вклад в
сигнальную компоненту после когерентного детектирования [1]. После когерентного
детектирования возникают синфазная и квадратичная составляющие полезного
сигнала, при этом вклад в сигнальную компоненту вносит только синфазная часть.
Определим мощности синфазной
вносит вклад в
сигнальную компоненту после когерентного детектирования [1]. После когерентного
детектирования возникают синфазная и квадратичная составляющие полезного
сигнала, при этом вклад в сигнальную компоненту вносит только синфазная часть.
Определим мощности синфазной ![]() и квадратичной
и квадратичной ![]() компонент принимаемого сигнала. Заметим,
что угол между двумя случайными величинами
компонент принимаемого сигнала. Заметим,
что угол между двумя случайными величинами ![]() и
и ![]() определяется как
определяется как
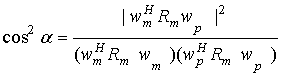
Полезный
сигнал ![]() может быть разложен на
синфазную и квадратурную составляющие как
может быть разложен на
синфазную и квадратурную составляющие как ![]() и
и ![]() . Соответственно, мощности синфазной и
квадратурной составляющих могут быть записаны как
. Соответственно, мощности синфазной и
квадратурной составляющих могут быть записаны как
![]() ,
, ![]()
И окончательно получаем,
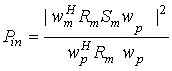 ,
,
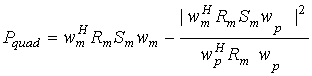 (3)
(3)
Нетрудно
видеть, что если весовые вектора полезного сигнала и пилот сигнала совпадают ![]() , то
, то ![]() . В классической
постановке, ОСШ на входе для m-ого пользователя может быть записан как
. В классической
постановке, ОСШ на входе для m-ого пользователя может быть записан как
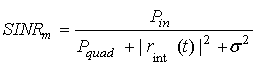
где
![]() - мощность независимого гауссова собственного
шума канала. Поскольку мощность внешних помех определяется собственными
весовыми векторами и не зависит от выбора весового вектора для
рассматриваемого m-ого
пользователя, то максимизация ОСШ может быть проведена с использованием
классических алгоритмов, используемых в адаптивных антеннах. Однако, такое решение
не учитывает влияние, которое оказывает сигнал m-ого пользователя на других
пользователей в рассматриваемой соте и в других сотах. Запишем суммарный сигнал
от m-ого пользователя,
принимаемый другими пользователями в рассматриваемой соте как
- мощность независимого гауссова собственного
шума канала. Поскольку мощность внешних помех определяется собственными
весовыми векторами и не зависит от выбора весового вектора для
рассматриваемого m-ого
пользователя, то максимизация ОСШ может быть проведена с использованием
классических алгоритмов, используемых в адаптивных антеннах. Однако, такое решение
не учитывает влияние, которое оказывает сигнал m-ого пользователя на других
пользователей в рассматриваемой соте и в других сотах. Запишем суммарный сигнал
от m-ого пользователя,
принимаемый другими пользователями в рассматриваемой соте как ![]() и пользователями в
других соседних сотах как
и пользователями в
других соседних сотах как ![]() с мощностями,
соответственно
с мощностями,
соответственно
![]() ,
, ![]() (4)
(4)
где
![]() - вектор отклика канала
в направлении от базовой станции на пользователей другой ячейки с ковариацонной
матрицей
- вектор отклика канала
в направлении от базовой станции на пользователей другой ячейки с ковариацонной
матрицей ![]() . Для выбора
оптимального весового вектора на передающей антенне для m-ого пользователя введем
следующее выражение для ОСШ
. Для выбора
оптимального весового вектора на передающей антенне для m-ого пользователя введем
следующее выражение для ОСШ
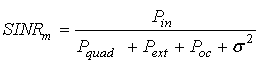 (5)
(5)
Фактически (5) не является реальным ОСШ, которое можеть быть измерено на приемнике. В некотором смысле, это виртуальная величина, максимизация которой позволяет соблюсти баланс между фазовыми рассогласованиями в системе и влиянием на других пользователей как в рассматриваемой соте, так и в соседних. Выражение для оптимального весового вектора, максимизирующего (5) нетрудно получить с учетом (3)-(4), используя метод множителей Лагранжа. Можно показать, что оптимальный весовой вектор для передающей АР и максимизирующий (5), запишется в виде
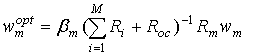 ,
(6)
,
(6)
где ![]()
Рассмотрим оптимальный передающий вектор при использовании индивидуального пилот сигнала (2). Поскольку для этого случая фазовые рассогласования между пилот сигналом и полезным отсутствуют, то
![]() и
и ![]()
Тогда выражение для ОСШ примет вид
Также используя метод множителей Лагранжа, получим для оптимального вектора в случае использования индивидуальных пилот сигналов
![]() собственный вектор,
соответствующий максимальному собственному числу матрицы
собственный вектор,
соответствующий максимальному собственному числу матрицы 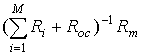 (7)
(7)
Сравнивая (6) и (7), можно найти общие и различные черты между двумя решениями. Оба решения пытаются усилить мощность сигнала в направлении на желаемый сигнал и уменьшить в направлениях на других пользователей. В то же время, поскольку использование индивидуального пилот сигнала практически решает проблему фазовых рассогласований, ожидается , что эффективность работы таких систем будет выше, хотя несомненно дороже с точки зрения технической реализации.
Данная
работа была частично поддержана Российским фондом фундаментальных исследований
(грант № 08-02-00818.).
Литература
1. J.Liberti, T.Rappaport, Smart Antennas for Wireless Communications. New Jersey. USA. Prentice Hall. 1999.
2. Winters J. // IEEE Personal Communication Magazine. 1998. N2. P.23.
3. Foschini G.J. , Gans M.J.// Wireless Personal Communications. 1998. V.6. N.4. P.311.
4. Friedlander B., Scherzer S. // Proc. Asilomar Conf. 2001.P.1014.
