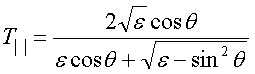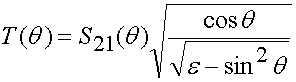Использование каналов Флоке для моделирования периодической наноструктуры
А. А. Курушин
Московский энергетический институт
Получена 7 октября 2010 г., после доработки - 22 ноября 2010 г.
Аннотация. С помощью программ HFSS и CST MWS выполнен анализ падения плоской волны на границу двух сред и проведено сравнение численного решения с аналитическим. Для моделирования структуры бесконечного размера с периодически повторяющимися фрагментами были использованы каналы Флоке. Рассчитаны коэффициенты отражения и передачи плоской волны через границу, на которой с плотностью 5% размещены конические структуры. Такая поверхность, применяемая в оптических усилителях, имеет частотную характеристику отражения и прохождения, зависящую от угла падения на неё плоской волны. Проведено сравнение полученных результатов расчета коэффициента отражения с экспериментальными данными, приведенными в литературе.
Ключевые слова: оптическая структура, падение плоской волны на границу раздела двух сред, каналы Флоке, оптический усилитель.
Введение
При проектировании оптических приборов необходимо оптимизировать их характеристики путем подбора параметров отражающей поверхности [1,2].
Целью данной работы является определение электродинамических характеристик структуры, состоящей из периодически расположенных металлических конусов, которая считается перспективной для создания нелинейных приборов оптического диапазона (см. рис. 1). Это могут быть оптические усилители, преобразователи и др. приборы.
a) б)
в)
Рис. 1. Схема a) и топология б) оптического усилителя, в) фрагмент модели наноструктуры, используемой при создании оптических усилителей
Структуру шероховатой поверхности металла можно описать несколькими способами: как систему с полусферическими, эллиптическими, конусообразными окончаниями, так и систему с коническими выступами. Во всех случаях стоит задача расчета собственных частот и частотной характеристики частотно-селективной поверхности.
Электродинамическая формулировка задачи выглядит следующим образом: на бесконечную в плоскости XOY периодическую структуру падает из верхнего полупространства плоская волна. Требуется найти рассеянное структурой поле. Для решения задачи используем известные программы электродинамического моделирования High Frequency System Simulator (HFSS) [7] и CST Microwave Studio (MWS) [8].
Естественным методом анализа бесконечных периодических структур является применение условий периодичности, которые сводят задачу для бесконечной структуры к анализу одного периода. Указанные выше программы дают возможность задания периодических условий.
Следует отметить, что анализ падения плоской волны на бесконечную периодическую структуру является достаточно новой задачей в практике применения таких программных средств как HFSS и CST MWS. Поэтому, прежде чем перейти непосредственно к расчету структуры показанной на рис. 1, целесообразно численно с помощью аппарата периодических граничных условий решить тестовую задачу и сравнить численное решение с аналитическим. В качестве тестовой структуры была выбрана граница раздела двух сред. Для нее известно строгое аналитическое решение в виде коэффициентов отражения и прохождения плоских волн [1, 2], которые будем сравнивать с численными результатами.
1. Падение плоской волны на границу раздела двух сред
При падении плоской волны на поверхность раздела двух сред, её поляризация не меняется. Если вектор Е лежит в плоскости падения, то такая поляризация называется параллельной, если вектор E перпендикулярен плоскости падения – перпендикулярная поляризация.
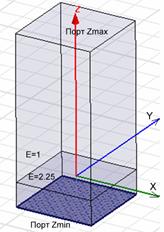
Для моделирования бесконечных периодических структур в программе HFSS используются периодические граничные условия, которые устанавливаются на противоположных сторонах бокса, охватывающих период анализируемой структуры. Пример использования граничных условий этого типа показан на рис. 2. Верхний параллелепипед заполнен вакуумом с диэлектрической проницаемостью равной единице, нижний – диэлектриком с относительной проницаемостью 2.25. Размер бокса по осям 0X и 0Y равен в данном примере 320 нм.
Бесконечная граница раздела двух сред, строго говоря, не является периодической структурой. Поэтому применение аппарата периодических граничных условий для ее анализа нуждается в пояснении.
Рассмотрим известное [2,4] представление поля внутри прямоугольного канала
Флоке. Под каналом Флоке понимается часть пространства, ограниченная
вертикальными стенками (см. рис. 2), на которых установлены периодические
граничные условия. Для прямоугольного канала Флоке составляющие поля E, H при ![]() имеют следующий
вид
имеют следующий
вид
где ![]() ,
,
![]() ,
,
![]() .
.
где ![]() – периоды повторения структуры по осям 0X и 0Y,
– периоды повторения структуры по осям 0X и 0Y, ![]() – амплитуды n, m гармоник,
– амплитуды n, m гармоник,
![]() - волновое
число свободного пространства.
- волновое
число свободного пространства.
Постоянные
![]() задаются
падающим полем, которое имеет вид плоской волны:
задаются
падающим полем, которое имеет вид плоской волны:
![]() ,
,
![]() ,
,
![]() -
меридиональный угол падения плоской волны, а
-
меридиональный угол падения плоской волны, а ![]() - азимутальный угол.
- азимутальный угол.
Ряд (1) называется
в теории периодических структур разложением поля по гармоникам Флоке, каждая из
которых является членом ряда (1). Можно увидеть, что гармоника Флоке с нулевыми
индексами ![]() , которую часто называют
основной гармоникой, имеет структуру поля, совпадающую с полем падающей волны.
Так как мы рассматриваем полупространство при
, которую часто называют
основной гармоникой, имеет структуру поля, совпадающую с полем падающей волны.
Так как мы рассматриваем полупространство при ![]() ,
то она описывает поле отраженной волны.
,
то она описывает поле отраженной волны.
Можно записать
разложение аналогичное (1) для полупространства при ![]() .
Основная гармоника в этом разложении будет соответствовать прошедшей
(преломленной) волне.
.
Основная гармоника в этом разложении будет соответствовать прошедшей
(преломленной) волне.
Гармоники высших порядков необходимы для описания ближнего поля, которое возбуждается, если период имеет сложную структуру, например, показанную на рис. 1 б,в. В случае плоской поверхности вид решения электродинамической задачи известен [1,2]. Поле описывается отраженной и преломленной волнами. Высшие гармоники Флоке не возбуждаются.
Таким образом, применение периодических граничных условий для анализа границы раздела двух сред оправданно тем, что отраженная и преломленная волны описываются основными гармониками Флоке, а гармоники высших порядков не возбуждаются.
Рис. 2. Фрагмент диэлектрической подложки, на которую падает плоская волна.
Интересно отметить, что поле основной гармоники
не зависит от периодов ![]() . Поэтому при решении тестовой
задачи их можно выбирать произвольным образом.
. Поэтому при решении тестовой
задачи их можно выбирать произвольным образом.
2. Решение задачи о падении плоской волны с помощью HFSS
Задание параметров падающей волны в системе HFSS поясняется на рис. 3. Угол падения связан с углом направления Eo, что задается в виде координат векторов k(-sin(Teta),0, sin(Teta)), Eo(-cos(Teta),0,sin(Teta)), которые устанавливаются в диалоге Incident Wave Source (рис. 3).
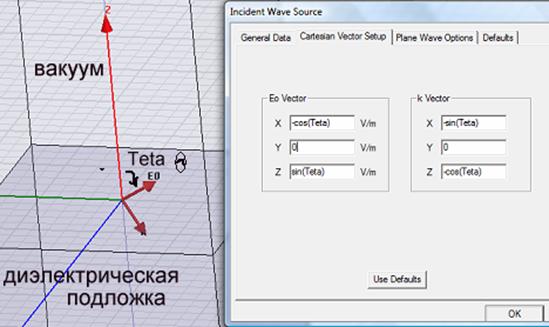
Рис. 3. Параметризация угла падения плоской волны: вектора распространения k и вектора электрического поля E.
Чтобы рассчитать характеристики отражения и преломления падающей волны под разными углами падения, будем изменять угол падения плоской волны Q в плоскости ZОX (f=0) в диапазоне 0…90°. В результате получаем картину поля, угол отражения и угол преломления электромагнитных волн. Для получения количественной оценки свойств частотно-селективной поверхности, применим теорему Флоке.
Для решения граничной задачи в системе HFSS на горизонтальных поверхностях, ограничивающих канал Флоке по вертикали необходимо установить порты, которые получили название портов Флоке.
Они задаются в диалоге показанном на рис. 4. Установим индексы n=0, m=0, а в качестве мод выберем поля TM (H) и TE (E).

Рис. 4. Установка параметров порта Флоке при решении задачи
Особенностью программы HFSS версии 12 является то, что порты Флоке можно ставить только на изотропную среду с диэлектрической проницаемостью равной единице.
Если между нижним портом Флоке и стороной нижней диэлектрической платы остается зазор (рис. 5), то в расчет вносится погрешность из-за вторичного отражения внутрь слоя. Необходимость создания такого зазора можно считать недостатком программы HFSS. Для того, чтобы такое вторичное отражение исключить, ставим снизу поглощающую границу Radiate, соприкасающуюся с нижней стороной диэлектрической платы. При этом мы теряем возможность расчета коэффициента прохождения через структуру, так как порт в нижней части канала Флоке заменяется указанной границей. Тем не менее, возможность расчета коэффициента отражения сохраняется.
Известны аналитические зависимости для коэффициента отражения и прохождения (передачи) при падении волны на границу раздела двух сред, т.е. при условии, что толщина платы стремится к бесконечности. Коэффициент отражения по полю для волны с параллельной поляризацией (рис. 7) равен [1]
где e - диэлектрическая проницаемость среды, на которую падает волна, Q - угол падения.
Коэффициент передачи поля для волны с параллельной поляризацией равен
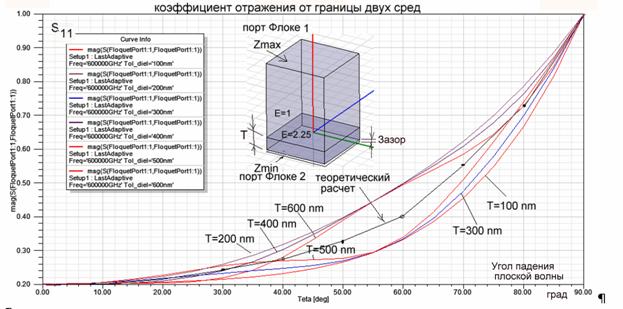
Расчеты, выполненные на HFSS и характеристики, рассчитанные по (2), сравниваются на рис. 5. Коэффициент отражения при θ=0º и θ=90º совпадают с теоретическими значениями R=0.2 и R=1. При других углах падениях имеется принципиальная ошибка, связанная с конечным значением толщины подложки T, показанной на рис. 5.
Рис. 5. Рассчитанный на HFSS коэффициент отражения в диапазоне углов падения для разных толщин подложки
На основе данных, приведенных на рис. 5 можно оценить погрешность зависимости коэффициента отражения по сравнению с аналитическим расчетом. Она составляет @ 10%. Полученная ошибка в расчетах объясняется тем, что невозможно создать условие полного поглощения волны, проходящей через подложку конечной толщины (как приходится делать в реальных условиях моделирования) даже используя поверхность типа Radiate.
3. Решение задачи о падении плоской волны с помощью CST MWS
Программа CST MWS [7] предоставляет больше возможностей для решения нашей задачи: в этой программе порты Флоке можно устанавливать на материал с проницаемостью отличной от единицы, в том числе, имеющей зависимость от частоты.
Выполним расчет с падением плоской волны на границу двух сред под разными углами на программе CST. Для описания бесконечной структуры применим периодические граничные условия, которые ставятся на боковых стенках блока Unit Cell. Сверху и снизу бокса анализа ставим порты Флоке. Причем: бокс для описания верхнего диэлектрика с Eps=1 не создаем, а задаем окружающее пространство (Background material, по терминологии CST), поднятое над диэлектриком с Eps=2.25.
Внизу порт Флоке можно установить непосредственно на сторону диэлектрического слоя, и в этом случае порт Флоке играет роль полного поглотителя.
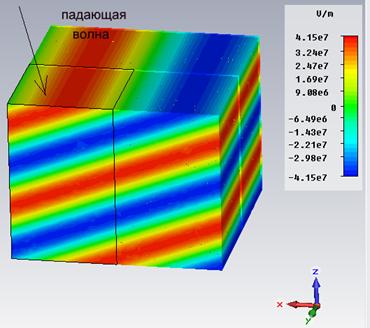
Рис. 6. Ячейка Unit Cell и волна, падающая параллельно плоскости XoZ
Направление падения плоской волны задается в виде разности фаз между противоположными границами при описании периодических граничных условий.
Граничные условия для ячейки Unit Cell автоматически повторяются в двух направлениях. Такой расчет можно выполнить только в частотной области. Во временной области, когда в CST MWS используется метод решения FDTD, можно выполнить анализ отражения и прохождения только падающей под углом Teta=0°. Это является свойством метода FDTD, поскольку в этом методе пространство разбивается на параллелепипеды
При установке порта Флоке необходимо выбрать параметр Number of Floquet modes - количество мод Флоке, которые будут учитываться в расчетах (рис. 7, 8).
Список мод Флоке может быть установлен вручную или автоматически. В последнем случае, максимальный порядок Флоке по двум направлениям может быть изменен, выбирая опцию Update. Количество мод зависит от размера блока Unit Cell. Чем больше её размер, тем больше типов волн нужно устанавливать. Для выбранных размеров Unit Cell (320 нм ´ 320 нм), можно выбрать минимальное число мод - фундаментальные типы волн Флоке TE (0,0) и TM (0,0), что соответствует моделированию падающей на поверхность плоской волны (рис. 7).
Постоянные распространения каждого типа волн рассчитываются после нажатия на Update и выводятся в строку данной моды.
|
Рис. 7. Установка 1 моды порта Флоке как поле E параллельной поляризации |
Рис. 8. Установка 1 моды порта Флоке как поле H перпендикулярной поляризации |
В разделе Frequency (рис. 7) введем частоту 600 ТГц, на которой рассчитываются коэффициент передачи S21 между портами Флоке, а также коэффициент отражения S11.
Рис. 9. Установка двух мод взаимноперпендикулярных волн на входе и выходе канала Флоке
Для того чтобы рассчитать коэффициенты отражения и прохождения в диапазоне углов падения, зададим угол падения как параметр Teta. Параметр Teta устанавливаем в двух местах: в описании граничных условий, по которому будет рассчитываться разность фаз между стенками Master и Slave, и в разделе «Sort evalution Point» диалога установок для портов Флоке (рис. 9).
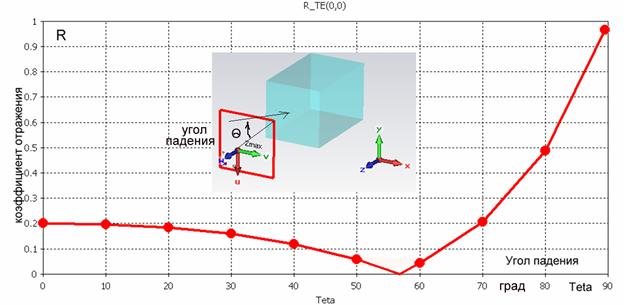
Рис. 10. Коэффициент отражения в случае параллельной поляризации (расчет по (2) и расчет на CST MWS совпадают). Угол Брюстера равен 57º, что также совпадает с аналитическим расчетом
Для вывода на график зависимость коэффициента отражения от угла падения (рис.10), нужно выполнить постобработку данных. В CST MWS это выполняется с помощью макросов, находящихся в разделе меню.
Порты Флоке позволяют рассчитать параметры рассеяния, которые определяются для волн с нормированными амплитудами [2]. Нормированная амплитуда по модулю равна корню квадратному из мощности, переносимой волной через поверхность единичной площади. В тоже время, формулы (2) и (3) записаны для амплитуд поперечных компонент электрического поля. Отличие в определении параметров рассеяния не сказывается при вычислении коэффициента отражения, поскольку падающая и отраженная волны распространяются в одной и той же среде нормируются одинаковым образом. При вычислении коэффициента прохождения разные способы записи параметров рассеяния приводят к разным количественным результатам. Поэтому для сравнения численных и аналитических расчетов необходимо найти связь между параметрами рассеяния определенными разными способами.
Запишем соотношения между полями падающей ![]() ,
отраженной
,
отраженной
![]() и
прошедшей
и
прошедшей ![]() волн:
волн:
![]() ,
, ![]() , где
R и
T – коэффициенты отражения и
прохождения по полю.
, где
R и
T – коэффициенты отражения и
прохождения по полю.
Мощность волны, преломленной в среду с проницаемостью e из среды с проницаемостью 1, равна [1,2]
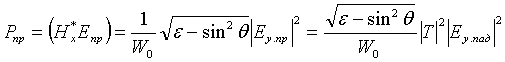 (4).
(4).
Мощность падающей волны равна
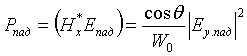 (5).
(5).
Используя (4) и (5), найдем связь между стандартным коэффициентом прохождения ![]() и
коэффициентом прохождения по полю
и
коэффициентом прохождения по полю ![]() :
:
Таким образом, для получения коэффициента передачи преломленной мощности в диэлектрическую среду для всех углов падающей волны нужно выполнить нормировку, заключающуюся в умножения коэффициента S21 на коэффициент пропорциональности из (6). Для того, чтобы непосредственно вывести коэффициент передачи на график, используем возможности постпроцессорной обработки пакета CST MWS.
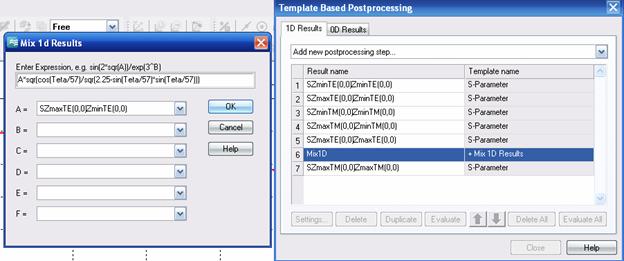
Рис. 11. Реализация расчета выражения для коэффициента передачи.
Программа CST MWS имеет большие возможности постпроцессорной обработки. Нормировку коэффициента передачи из (6) можно выполнить, вводя его выражение в макрос Mix 1d Results (рис. 11). В верхней строке введена формула (3). В строке A выбираются S параметры передачи мощности от порта с максимальной координатой Zmax до порта с минимальной координатой Zmin. В правом диалоге выбираются S параметры портов Флоке. Возможно также вывести по оси абсцисс не частоту, а длину волны, для чего нужно выполнить перенормировку по оси x.
4. Моделирование металла в оптическом диапазоне волн
В отличие от работы [3], где выполнен расчет частотно-селективной медной поверхности, в настоящей работе применяется более сложная модель металла, что актуально в диапазоне оптических волн.
Особенностью поведения металла в оптическом диапазоне является то, что её невозможно описать в рамках теории скин – эффекта. Необходимо использование более сложных моделей, которые рассматривают металл как среду, имеющую действительную и мнимую части диэлектрической проницаемости сравнимые по величине. Обе части диэлектрической проницаемости сильно зависят от частоты, а действительная часть может быть отрицательной.
На рис. 12 приведены экспериментальные частотные зависимости реальной и мнимой части диэлектрической проницаемости серебра. Проводимость металла можно оценивать по величине σ, который находится в пределах 3*107 см/м, или по тангенсу диэлектрических потерь, который зависит от отношения мнимой части к реальной части диэлектрической проницаемости на одной частоте
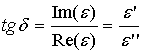 , (7)
, (7)
где
![]() .
.
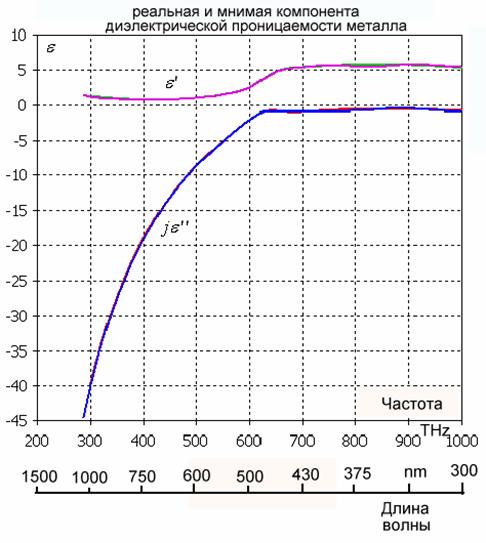
Рис. 12. Реальная и мнимая части серебра в оптическом диапазоне волн
В программах HFSS и CST можно выбрать и оптимизировать следующие дисперсионные модели материалов: модели Дебая 1-го и 2-го порядка, Друде, Лоренца. Выбор модели зависит от диапазона частот, в которой будет работать оптическая система. Модель Друде [5,6,10], встроенная в CST MWS (рис. 12) может описать характеристики плазмы, металла, и др. сред. Моделирование распространения волн в металле позволяет отказаться от граничных условий, применяемых на СВЧ - условий Леонтовича-Щукина, поверхностного сопротивления, и др. характеристик металла с потерями [2].
Диэлектрическая проницаемость материала в модели Друде имеет дисперсионный характер и следующим образом зависит от частоты:
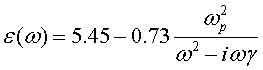 ,
(8)
,
(8)
где ωp=1.72·1016 1/сек и υe =8.35·1013
1/сек. Формула (8) обеспечивают хорошее согласование
с экспериментальными данными (см. рис. 12) в видимом и инфракрасном
диапазоне. При
![]() диэлектрическая
проницаемость стремится к величине 5.45.
диэлектрическая
проницаемость стремится к величине 5.45.
5. Анализ падения плоской волны на поверхность, используемую в оптических усилителях
Убедившись, что программа CST MWS численно решила задачу падения плоской волны с высокой точностью, можно выполнить анализ сложной резонансной структуры, на которую падает электромагнитная волна.
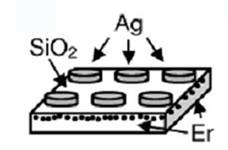
Такие поверхности применяются в оптических усилителях. С целью получения усиления люминесценции сред с редкоземельными ионами, обусловленного металлическими структурами, предлагается применение металлических поверхностей с расположенной на них системой наноразмерных конусов с шаровым окончанием (рис. 13), изготавливаемых с использованием трековых мембран [5,9]. Такие экспериментальные образцы конических наноструктур в настоящее время уже получены и выполнены спектрально- люминесцентные измерения для случая сред, содержащих ионы эрбия.

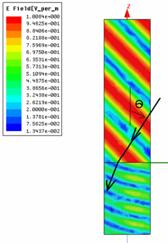
Рис. 13. Распределение компонентов напряженности поля вдоль линии a-a’, секущей конус и плоскость отражения
Поскольку известно, что конусы размещены с плотностью rs=8*108 см-2, то для получения относительной плотности s=1% один отражающий объект (конус с нижним диаметром 40 nm) нужно установить на площадку размером 320 nm ´ 320 nm. Для других плотностей расположения конических неоднородностей размеры приводятся в табл.1.
Отметим, что в реальности конусы распределены случайным образом, но для расчета мы используем модель в виде регулярной периодической структуры. Анализ характеристики поверхности с хаотически расположенными коническими остриями, как предполагается, можно выполнить, выделяя более крупный фрагмент поверхности, и размещая на нем несколько конических острий с произвольным размещением.
Табл. 1. Размеры конусов для обеспечения заданных плотностей расположения конусов на плоскости
|
s=s/S |
1% |
5% |
24% |
40% |
|
D, нм |
40 |
80 |
190 |
250 |
|
H, нм |
60 |
130 |
290 |
380 |
Диэлектрическая проницаемость металла (серебра или золота) задается в виде частотнозависимой модели Друде, причем частотная зависимости Reε и Imε в оптическом диапазоне волн 300-800 ТГц (или 200 -1500 nm) вводятся в CST MWS в табличном виде, полученном на основе экспериментально измеренных коэффициентов преломления оптического луча на границе сред.
Результаты расчета коэффициента отражения такой частотно-селективной поверхности приводится на рис. 14. Время расчета одной частотной точки 4 мин, на двухядерном компьютере с частотой процессора 2 ГГц, требуемая память 700 МБ.
Конусы, расположенные на поверхности диэлектрической подложки (рис. 1), работают как вторичные излучатели (монопольные антенны). Между ними существует связь. Волна, падающая на структуру по оси Z, возбуждает на поверхности и внутри структуры токи, которые создают вторичное отражение. Из рис. 14 можно видеть, что рассчитанные зависимости пересекаются в точке А, а экспериментальные зависимости [11] пересекаются в точке B, в которых меняется характер интенсивности отражения. Так, если до этой точки коэффициент отражения больший для Teta= 15° то для частот правее точки A коэффициент отражения больший для Teta=75°.
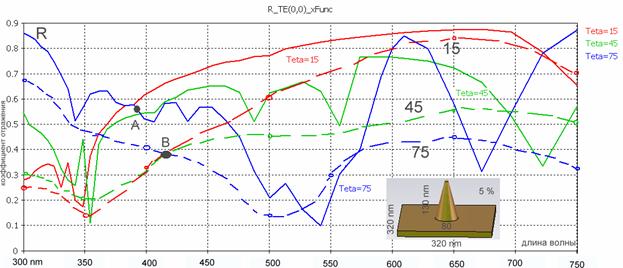
Рис.14. Коэффициенты отражения плоской волны при 5% плотности конических окончаний
На рис. 14. приводятся также, в виде пунктирных линий, экспериментальные зависимости, полученные в [10]. Несмотря за невысокую точность совпадения частотных характеристик коэффициента отражения для углов Teta=15°, 45° и 75° (в среднем 25%), можно видеть, что в расчете повторяется физическое явление, обнаруженное в эксперименте: изменение интенсивности отраженной волны в зависимости от угла падения и частоты (точка А в расчете и точка B в эксперименте). Это явление можно объяснить разной дифракцией падающей волны под разными углами падения.
В заключении можно отметить, что в настоящее время на оптических частотах применяются и другие, более сложные частотно-селективные поверхности. Так, резонансными свойствами обладает структура, в которую внедрены полые резонаторы, созданные травлением [11]. Размеры порядка десятков нанометров вполне доступны для современной технологии. В этом случае для создания высокодобротной резонансной структуры, которая активно меняет частотный спектр оптической волны, падающей на неё, можно использовать опыт, наработанный в области СВЧ и антенной техники. Так, возможно выполнить анализ светодиодных модулей, представленных как система резонаторов с квантовыми точками в форме слоев, нитей, точек и дисков [9,11].
Заключение
Для моделирования падения электромагнитных волн оптического диапазона на металлические поверхности со сложной структурой можно использовать методы расчета как в частотной области (метод конечных элементов FEM), так и во временной области (метод конечных разностей во временной области FDTD)
В рамках решения поставленной задачи были выполнены расчеты характеристик отражения и прохождения плоской волны через границу двух сред. Результаты численных расчетов совпали с результатами известной аналитической модели.
При решении данной тестовой задачи было отдано предпочтение программе CST MWS, поскольку она позволяет использовать порты Флоке расположенные на поверхности диэлектрика.
В качестве практического примера рассмотрено моделирование поверхности, состоящей из конических металлических наноструктур, используемых для усиления люминесценции в оптическом усилителе. Расчеты показали качественное совпадение электродинамических характеристик поверхности с экспериментальными данными.
Литература
1. Нефедов Е.И. Антенно-фидерные устройства и распространение радиоволн. – 2-е изд. – М: «Академия», 2008, - 320 с.
2. Нефедов Е.И. Техническая электродинамика. – М., «Академия»., 2008, - 416 с.
3. Gutzeit E., Kurushin A., Maslov V. Design Nanosize Light Modules. II Forum Nanotechnology, Moscow 2009, Theses, Vol.II.
4. Баскаков С.И. Основы электродинамики. М., «Сов. Радио», 1973, 248 с.3.
5. P. Montgomery, "Scattering by an Infinite Periodic Array of thin Conductors on a Dielectric Sheet", IEEE Trans on Ant Prop, Vol Ap - 23, No. 1, Jan 1975.
6. Mertens H., Verhoeven J., Polman A., Tichelaar F.D. Appl. Phys.Lett. 2004. V.85. P.1317.
7. www.ansoft.com – сайт компании Ansoft.
8. www.cst.com - сайт компании CST.
9. Банков С.Е., Курушин А.А. Проектирование и оптимизация СВЧ структур с помощью HFSS Ansoft. М., Солон-Пресс. 2005, 240 стр.
10. Denisenko G.A., Gutzeit E.M., Kurushin A.A. Electrodynamics Modeling of Nanosized Optical Systems. 4th International Conference od Physics of Laser
Crystals. Sudak, Crimea, 12-16 September 2010, Kharkiv-Sudak, p. OC10.
11. В.А.Олейников, К.В.Соколов, И.Р.Набиев. Спектры отражения при воздействие на острийные структуры Ag падающей волны. ЖПС, 59,
123,1993.

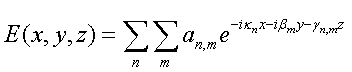 , (1)
, (1)
 , (2)
, (2)