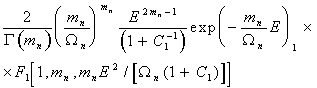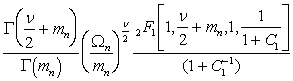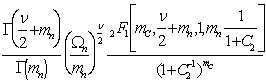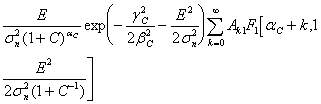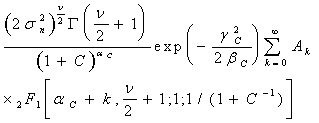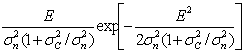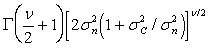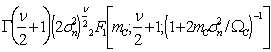УДК 621.391
СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ СМЕСЕЙ НЕГАУССОВСКОГО РАДИОЛОКАЦИОННОГО СИГНАЛА И НЕГАУССОВСКОЙ ПОМЕХИ
А. В. Болдин, А. А. Бортников, Ю. А. Мурашкин, А. В. Хомяков
ОАО Центральное конструкторское бюро аппаратостроения, г. Тула
Получена 26 октября 2011 г.
Аннотация. Получены и исследованы вероятностные характеристики параметров негауссовских частично поляризованных сигналов при наличии негауссовской помехи. Получены оценки параметров моделей через физически измеряемые величины. Модели могут быть использованы для статистического описания сигналов, у которых флуктуации амплитуд имеют более глубокий характер, чем у релеевской модели.
Ключевые слова: статистические характеристики, радиолокационный сигнал, негауссовское распределение, периодически нестационарный сигнал.
Abstract. There have been obtained and researched probabilistic characteristics of non- Gaussian signal parameters in the presence of non- Gaussian disturbance. The models can be used for statistical description of signals with a deeper nature of amplitude fluctuation comparing to that of a Rayleigh model.
Key words: statistics, a radar signal, non – Gaussian distribution, a periodically non-stationary signal.
Введение
При разработке радиолокационных систем обнаружения и измерения координат малоразмерных целей в условиях воздействия естественных и преднамеренных помех, необходимо знание вероятностных характеристик параметров (амплитудных, фазовых, поляризационных) смеси полезного сигнала и помехи. Известно достаточное количество работ, в которых приведены указанные характеристики, однако в качестве исходных распределений сигнала использованы модели Рэлея, Райса, Накагами, справедливые лишь для ограниченного числа объектов наблюдения, секторов, углов наблюдения, среды распространения и типа подстилающей поверхности. а в качестве помехи – гаусссовская помеха или варианты полигауссовских распределений [1-3].
Причинами отличия
вероятностной модели сигнала от гауссовской могут служить: ограниченное число
"блестящих" точек объекта наблюдения, принимающих участие в
формировании отраженного сигнала (нарушение центральной предельной
теоремы), искажение гауссовских сигналов под воздействием помех, нелинейные
преобразования во входных цепях приемника. Накопленный к настоящему времени
экспериментальный материал подтверждает негауссовский характер флуктуаций
сигналов, отраженных от объектов. Так, например, в работах [4,5] показано,
что коэффициент вариаций огибающей превышает величину 0,53, справедливую для
релеевской модели, практически у 70% обработанных реализаций, полученных для
радиолокационных целей в миллиметровом диапазоне волн. Наиболее ярко это
проявляется в коротковолновой части сантиметрового и миллиметровом диапазонах,
при малых углах скольжения (менее 5 0) , узкой диаграмме
направленности антенны (ДНА) ![]() от 15' до 1 град. и высокой разрешающей
способности по дальности (длительности зондирующего импульса tn Î(0,01¸0,33) мкс). Следовательно, при
синтезе и анализе РЛС обнаружения и распознавания РЛО необходимо учитывать
негауссовский характер флуктуаций отраженных сигналов, используя для описания
их вероятностных характеристик достаточно общие модели, включающие как частные
случаи наиболее используемые модели.
от 15' до 1 град. и высокой разрешающей
способности по дальности (длительности зондирующего импульса tn Î(0,01¸0,33) мкс). Следовательно, при
синтезе и анализе РЛС обнаружения и распознавания РЛО необходимо учитывать
негауссовский характер флуктуаций отраженных сигналов, используя для описания
их вероятностных характеристик достаточно общие модели, включающие как частные
случаи наиболее используемые модели.
Целью работы является получение и исследование вероятностных характеристик параметров негауссовских частично поляризованных сигналов при наличии негауссовской помехи.
В соответствии с феноменологической моделью, полностью приведенной в [5,6], представим наземный объект в виде n отражающих групп блестящих точек (БТ). Каждая из этих групп, в свою очередь, состоит из j БТ, одна из которых является доминирующей, то есть обладает большей отражающей способностью, чем каждая из (j - 1) оставшихся БТ. Считая, что сигналы, отраженные от k - тых групп являются узкополосными и не зависят от сигналов, отраженных от других групп, для плотности распределения вероятностей (ПРВ) огибающей сигнала на выходе детектора приемника будет справедливо соотношение
В соответствии с рассмотренной
феноменологической моделью отраженного негауссовского сигнала, можно дать
следующую физическую интерпретацию ![]() ,
, ![]() и
и ![]() . Параметр
. Параметр ![]() ,учитывающий число отражающих групп лоцируемого
объекта, характеризует глубину флуктуаций ортогонально поляризованных
компонент негауссовского сигнала; параметр
,учитывающий число отражающих групп лоцируемого
объекта, характеризует глубину флуктуаций ортогонально поляризованных
компонент негауссовского сигнала; параметр ![]() характеризует отношение детерминированной
составляющей сигнала к его дисперсии, а параметр
характеризует отношение детерминированной
составляющей сигнала к его дисперсии, а параметр ![]() - обратно пропорционален дисперсии.
- обратно пропорционален дисперсии.
Рассмотрим вероятностную модель
помехи. Для этого, как и выше, используя феноменологический подход, полагаем,
что суммарная помеха на входе приемника РТС формируется ![]() -ым количеством источников помех,
каждый из которых создает гауссовский помеховый сигнал с математическим
ожиданием равным нулю. При этом квадратурные составляющие сигнала некоррелированы.
Тогда, нетрудно показать, что одномерная плотность распределения вероятностей
огибающей негауссовской помехи будет иметь вид
-ым количеством источников помех,
каждый из которых создает гауссовский помеховый сигнал с математическим
ожиданием равным нулю. При этом квадратурные составляющие сигнала некоррелированы.
Тогда, нетрудно показать, что одномерная плотность распределения вероятностей
огибающей негауссовской помехи будет иметь вид
На рис. 1 представлены семейства кривых ПРВ W(Eп), построенных по формуле (3), при различных значениях параметров aп и bп . Видно, что указанные параметры существенно влияют на форму кривых и на числовые характеристики огибающей Еп. Отметим, что для оценки параметров aп и bп распределения (3) могут быть использованы выражения [5,6]
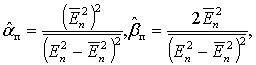 (4)
(4)
Из (3) при ![]() =1 и
=1 и ![]() =1/2
=1/2![]() следует распределение Релея.
следует распределение Релея.
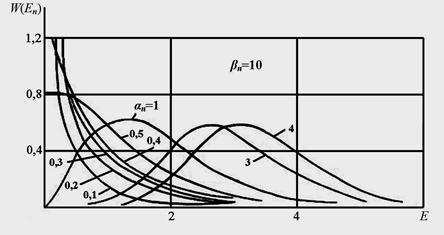
Рис. 1. Зависимости ПРВ ![]() от параметров
от параметров ![]() и
и ![]() .
.
Будем полагать, что огибающая полезного сигнала подчиняется распределению (1), а огибающая помехи - распределению (3). Как показано в [5,6], распределение (1) можно представить в виде обобщенной условной плотности распределения вероятностей огибающей Е аддитивной смеси детерминированного сигнала и негауссовской помехи
где ![]() >
0,
>
0, ![]() >
0 - параметры помехи; Ес - огибающая сигнала.
>
0 - параметры помехи; Ес - огибающая сигнала.
При отсутствии сигнала Ес = 0, распределение (5) трансформируется в распределение негауссовой помехи (3).
Если сигнал флуктуирует, то безусловную ПРВ огибающей смеси сигнала и помехи можно определить по байесовскому правилу [7]:
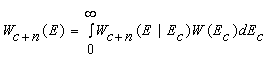 (6)
(6)
Полагая, что огибающая негауссового
сигнала Ес описывается обобщенной ПРВ (1) и подставляя в (6)
выражения (5) и (1), а затем разложив функцию Бесселя ![]() в ряд, после интегрирования
получим искомую ПРВ:
в ряд, после интегрирования
получим искомую ПРВ:
где ![]() ,
, 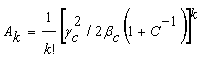
Из (7) следует, что ПРВ негауссового
сигнала при наличии негауссовой помехи полностью определяется пятью параметрами
![]() ,
, ![]() ,
, ![]() и
и ![]() . Первые три параметра
характеризуют статистические свойства сигнала, последние два - помехи. При этом
параметры,
. Первые три параметра
характеризуют статистические свойства сигнала, последние два - помехи. При этом
параметры, ![]()
![]() ,
, ![]() характеризуют глубину флуктуаций,
параметры
характеризуют глубину флуктуаций,
параметры ![]()
![]() - величину, обратную
дисперсиям сигнала и помехи, параметр
- величину, обратную
дисперсиям сигнала и помехи, параметр ![]() .
.
При отсутствии детерминированной амплитуды сигнала соотношение (7) упрощается
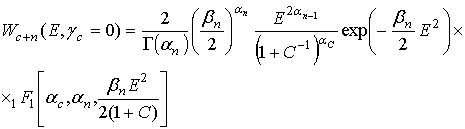 . (8)
. (8)
Используя асимптотическое разложение
вырожденной гипергеометрической функции, нетрудно показать, что при дисперсии
помехи ![]() выражения
(7) и (8) переходят соответственно в (3) и (1).
выражения
(7) и (8) переходят соответственно в (3) и (1).
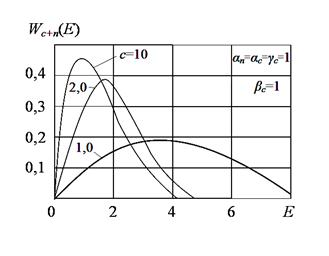
На рис. 2 (а,б) представлены
семейства кривых ПРВ (7) и (8) соответственно при некоторых значениях
параметров ![]() и
и
![]() . Из рисунков
следует, что изменение указанных параметров приводит к трансформации ПРВ
огибающей смеси сигнала и негауссовой помехи.
. Из рисунков
следует, что изменение указанных параметров приводит к трансформации ПРВ
огибающей смеси сигнала и негауссовой помехи.
Для определения n - х начальных моментов
|
|
|
|
а) |
б) |
Рис. 2. Плотность распределения вероятностей ![]() при некоторых
значениях параметров
при некоторых
значениях параметров ![]() и
и
![]() .
.
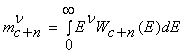 (9)
(9)
подставим (7) в (9) и перейдем к новой переменной Z = E2. Используя при интегрировании преобразование Меллина [8], получим
Интегральную функцию распределения смеси сигнала и помехи 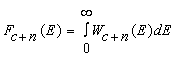 можно определить,
разложив функцию
можно определить,
разложив функцию![]() из (7) в ряд, а затем проинтегрировав по переменной Е.
из (7) в ряд, а затем проинтегрировав по переменной Е.
В результате будем иметь
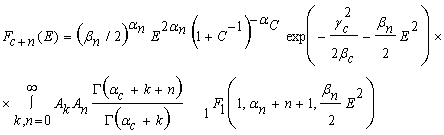 (11)
(11)
где
![]() .
.
Для получения частных случаев достаточно в (7), (10) и (11) подставить те или иные значения параметров ai, bi и gс. Частные случаи представлены в табл. 1. Некоторые из них получены ранее в работах [5,6,9].
При выводе обобщенной вероятностной
модели (3) было сделано предположение о независимости квадратурных составляющих
x, y отраженного сигнала. При рассмотрении более общего случая,
когда квадратурные составляющие коррелированны между собой с коэффициентом
корреляции r и имеют
разные дисперсии ![]() ,
по приведенной выше методике получены основные характеристики для аддитивной
смеси периодически нестационарного сигнала и помехи, подчиненной распределению
(3). Исходным распределением для этого является также обобщенная условная ПРВ (5).
После ряда преобразований получим
,
по приведенной выше методике получены основные характеристики для аддитивной
смеси периодически нестационарного сигнала и помехи, подчиненной распределению
(3). Исходным распределением для этого является также обобщенная условная ПРВ (5).
После ряда преобразований получим
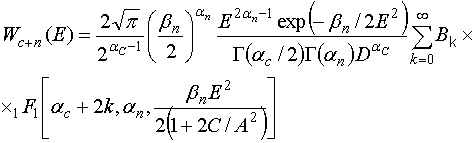 (12)
(12)
где
![]() ;
;
![]()
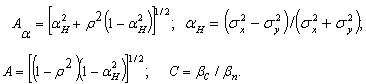
Отсюда нетрудно определить интегральную функцию распределения
![]() и начальные моменты
и начальные моменты
![]() соответственно.
соответственно.
В качестве заключения к разделу можно сделать следующие выводы.
1. Феноменологический подход при синтезе моделей сигналов, отраженных от объектов приводит к двум видам обобщенных негауссовых моделей: обобщенной негауссовой модели стационарных сигналов и обобщенной негауссовой модели периодически нестационарных сигналов. Первая модель не учитывает корреляции между квадратурными составляющими сигнала и включает, как частные случаи, другие модели (Рэлея, Райса, Хойта, Накагами, однодоминатное плюс релеевское распределение, распределение Максвелла-Больцмана, одностороннее нормальное распределение). Вторая модель учитывает корреляцию квадратурных составляющих и включает, как частные случаи, модели: Рэлея, Накагами, Хойта, r- распределение, гауссовое периодически- нестационарное распределение.
2. Анализ синтезированных вероятностей моделей и статистических характеристик огибающей, полученных на основе ПРВ W(E), показывает, что эти модели могут быть использованы для статистического описания сигналов, у которых флуктуации амплитуд имеют более глубокий характер, чем у релеевской модели.
3. Получены оценки параметров моделей через физически измеряемые величины и показано, что эти параметры связаны с глубиной флуктуаций отраженного сигнала (параметр aС), средней мощностью сигнала (параметры bс или W), стабильной составляющей цели (параметр gс) и нестационарностью сигнала (параметр bн).
4. Наличие мощных мешающих отражений при решении задач обнаружения и пеленгации целей, а также вероятность наличия организованных помех, приводит к необходимости их учета на этапе проектирования РЛС. Для этого получены вероятностные модели для смесей негауссовых сигналов и помех и исследованы их характеристики. Полученные выражения обобщают многочисленные частные случаи, имеющие место на практике и в теории синтеза РЛС.
Таблица 1. Частные случаи статистических характеристик смеси негауссовских сигналов и помех.
|
Параметры |
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
0 |
1 |
|
|
|
|
|
|
0 |
1 |
|
|
|
Литература
1.Быстров Р.П., Засовин Э.А. Потапов А.А., Соколов А.В. и др. Радиолокационные системы: научно-технические достижения и проблемы развития техники миллиметрового диапазона радиоволн // Зарубежная радиоэлектроника. Успехи современной радиоэлектроники. 2001. № 4 (ч. 1–3) и № 5 (ч. 4, 5).
2. Островитянов Р.В., Басалов Ф.А. Статистическая теория радиолокации протяженных целей. М.: Радио и связь. 1982. - 232 с.
3. Костылев В.И., Сличенко М,П. Адаптивное энергетическое обнаружение квазидетерминированных радиосигналов на фоне негауссовского шума// Радиотехника и электроника. Том 56. №6. 2011. - с. 698-704.
4. Быстров Р.П., Дмитриев В.Г., Потапов А. А., Соколов А.В. Проблемы радиолокационного обнаружения, малоконтрастных объектов. Монография " Вопросы перспективной радиолокации". Под ред. А.В.Соколова. //М.: Радиотехника. 2003. - с.2-48.
5. Акиншин Н.С., Быстров Р.П., Румянцев В.Л., Соколов А.В. Миллиметровая радиолокация: методы обнаружения негауссовских сигналов, Под ред.Р.П. Быстрова. // М: Радиотехника. 2010. - 528 с.
6. Мелитицкий В.А., Акиншин Н.С., Михайлов А.В., Румянцев В.Л. Оценка параметров распределения мощности негауссовского сигнала. // М.: «Радиотехника и электроника» . 1984. №4. - с.797-800.
7. Тихонов В.И. Статистическая радиотехника. // М.: Радио и связь. 1982. - 623 с.
8. Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. //М.: Наука. 1981. 797 с.
9. Акиншин Н.С., Румянцев В.Л., Процюк С.В. Поляризационная селекция и распознавание радиолокационных сигналов. //Тула: Лидар. 2000. -316 с.
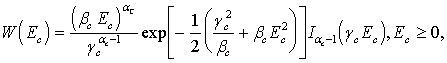
 (3)
(3) 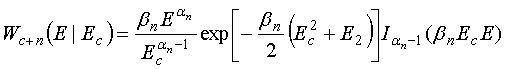 , (5)
, (5)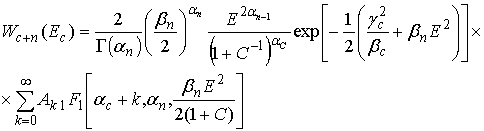 , (7)
, (7)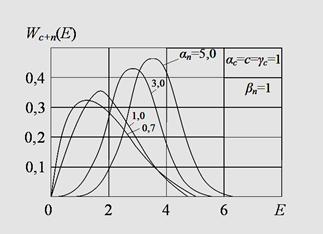
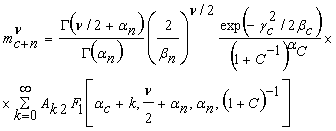 . (10)
. (10)