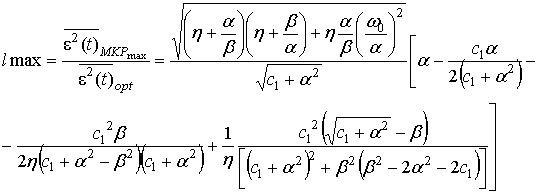УДК 681.513.6
О ВЫДЕЛЕНИИ ГАУССОВО-МАРКОВСКОГО СИГНАЛА НА ФОНЕ УЗКОПОЛОСНОЙ НОРМАЛЬНОЙ ПОМЕХИ МОДЕЛЬНЫМ КОМПЕНСАТОРОМ ПОМЕХ
А. Е. Манохин
институт радиоэлектроники и информационных технологий-РТФ УрФУ им. первого Президента РФ Б.Н.Ельцина, кафедра радиоэлектронных и телекоммуникационных систем, Екатеринбург
Получена 13 ноября 2011 г.
Аннотация. В работе решается задача выделения двухканальным модельным компенсатором помех гауссово-марковского процесса, действующего на фоне узкополосной нормальной помехи. Ставится обязательное условие, что помехи в каналах взаимно некоррелированы.
Ключевые слова: модельный компенсатор помех, формирующий белый шум, оптимальный фильтр.
Abstract. In the work the problem of extracting Gaussian-Markovian process, acting on the background of narrow-band normal disturbances by the two-channel model disturbances canceller is solved. The obligatory condition is put, that disturbances in channels are mutually non-correlative.
Keywords: model disturbance canceller, forming white noise, optimal filter.
Введение
В [1] решалась задача фильтрации гауссово-марковского процесса, действующего на фоне белого гауссова шума, когда помехи в каналах взаимно некоррелированы, с помощью модельного компенсатора помех.
В данной работе вводятся более сложные условия фильтрации, а именно выделение гауссово-марковского процесса, действующего на фоне узкополосного нормального процесса (УНП). Пусть на вход компенсатора поступает полезный сигнал в виде гауссово-марковского процесса со спектральной плотностью:
![]()
и помеха – узкополосный нормальный процесс со спектральной плотностью:
![]()
где ![]() - мощность
гауссово-марковского процесса;
- мощность
гауссово-марковского процесса; ![]() - мощность узкополосного нормального процесса,
α и β – нормированная к полосе белого шума ширина спектра
гауссово-марковского и узкополосного нормального процессов соответственно;
- мощность узкополосного нормального процесса,
α и β – нормированная к полосе белого шума ширина спектра
гауссово-марковского и узкополосного нормального процессов соответственно; ![]() ; f0 – нормированная к полосе белого шума центральная
частота УНП.
; f0 – нормированная к полосе белого шума центральная
частота УНП.
В компенсационном канале действует узкополосная нормальная помеха d2, совпадающая по корреляционной функции с помехой в основном канале d1, но некоррелированная с ней. Такая ситуация может возникнуть, например, при разнесенной во времени записи зашумленного сигнала в основном канале и помехи в опорном канале. В этом случае временной сдвиг фаз между помехами в каналах будет много больше памяти фильтра и не позволит обычным адаптивным способом выровнять задержку в канале.
Применение модельного компенсатора
Автором предлагается, как и в случае с «белой» помехой, использовать модельный компенсатор помех, который хорошо работает при слабой взаимной корреляции или абсолютной некоррелированности помех на обоих его входах. Подробный алгоритм работы модельного компенсатора помех изложен в [1].
При равенстве отношения мощности помеха-формирующий шум в сигнальном канале и отношения мощности помеха-формирующий шум в компенсационном канале передаточная характеристика модельного компенсатора может быть представлена в виде [1]:
где Ss(ω) – спектральная плотность мощности сигнала; Sd(ω) – спектральная плотность мощности помехи в каналах; Sν(ω) – спектральная плотность мощности формирующего белого шума в каналах.
Найдем выражение для дисперсии ошибки на выходе оптимального винеровского фильтра, когда в качестве полезного сигнала выступает гауссово-марковский процесс, а помехой – УНП.
 (2)
(2)
где η – отношение мощности сигнал-помеха.
При вещественном характере коэффициента передачи модельного компенсатора помех дисперсию ошибки фильтрации на его выходе можно оценить по формуле [2,с.53]:
Найдем коэффициент передачи модельного компенсатора, подставляя спектральные плотности сигнала и помехи в формулу (1):
где q2
– отношение мощности помеха-формирующий шум в каналах; ![]() ;
;![]() .
.
Если установить отношение мощности помеха-формирующий шум в каналах много
меньше единицы, тогда ![]() ,
и этим коэффициентом (c2) можно
пренебречь. В этом случае коэффициент передачи модельного компенсатора
упрощается:
,
и этим коэффициентом (c2) можно
пренебречь. В этом случае коэффициент передачи модельного компенсатора
упрощается:
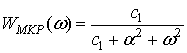 (5)
(5)
Подставим выражение для коэффициента передачи (5) в формулу (3):
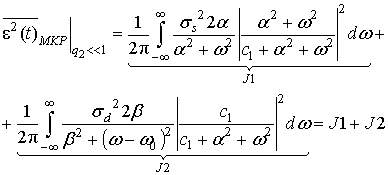 (6)
(6)
Ввиду громоздкости вычисления интеграла J2, найдем предельное значение дисперсии ошибки фильтрации при нулевой центральной частоте УНП. Тогда выражение (6) можно преобразовать к виду:
 (7)
(7)
Затем найдем предельный относительный проигрыш оптимальному фильтру:
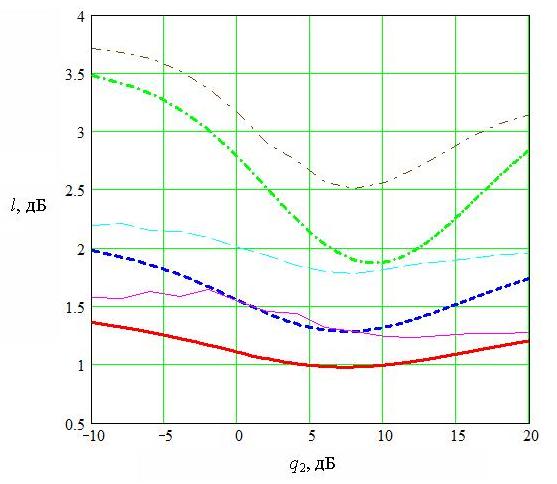
Полученное по ф.8 значение проигрыша является его верхней границей при малых отношениях мощности помеха-формирующий шум. На рисунке 1 изображены расчетные зависимости предельного проигрыша lmax (полученного по формуле (8)) и полного проигрыша l (рассчитанного путем численного интегрирования выражения 3 с подстановкой в него формулы (4)) от отношения мощности помеха-формирующий шум.

Рис.1. Расчетная зависимость предельного проигрыша lmax (толстая линия) и полного проигрыша l (тонкая линия) от отношения помеха-формирующий шум q2 при ω0=0 (сплошная), ω0=π/2 (пунктирная), α=0.7, β=0.1, η=-10дБ
Анализ зависимости на рисунке 1 показывает, что формула 8 хорошо аппроксимирует значение проигрыша при малых отношениях мощности помеха-формирующий шум q2. Кроме того, зависимость проигрыша, полученная путем численного интегрирования выражения 3 (тонкая линия), свидетельствует о наличии оптимального значения q2, при котором полный проигрыш минимален.
Компьютерное моделирование
С помощью разработанного программного обеспечения «Модельный компенсатор помех» было проведено моделирование работы разработанного алгоритма подавления помех. Получены следующие результаты.
Исследовалась зависимость проигрыша оптимальному фильтру l от отношения помеха-формирующий шум q2 при разных значениях отношения мощности сигнал-помеха η и центральной частоты ω0. Параметры моделирования отображены в таблице 1, результаты моделирования показаны на рисунках 2-4. Полезный сигнал – гауссово-марковский процесс с полосой α. Помеха – узкополосный нормальный процесс с полосой β и центральной частотой ω0, помехи в каналах некоррелированы.
Таблица 1. Параметры моделирования
|
Параметр |
Значение |
|
Ширина полосы сигнала α |
0.7 |
|
Ширина полосы помехи β |
0.1 |
|
Центральная частота помехи ω0 |
π/8; π/4; π/2 |
|
Объем выборки для оценки l |
65536 |
|
Количество выборок для усреднения l |
5 |
|
Число весовых коэффициентов |
512 |
|
Коэффициент адаптации |
0.01 |
|
Алгоритм адаптации фильтров |
метод наименьших квадратов [3] |
Рис.2. Зависимость проигрыша l от отношения помеха-формирующий шум q2 (расчетная – толстая линия, моделируемая – тонкая линия) при ω0= π/8 (сплошная), ω0=π/4 (пунктирная), ω0=π/2 (штрихпунктирная), α=0.7, β=0.1, η=-10дБ
Рис.3. Зависимость проигрыша l от отношения помеха-формирующий шум q2 (расчетная – толстая линия, моделируемая – тонкая линия) при η=-10дБ (сплошная), η=0дБ (пунктирная), α=0.7, β=0.1, ω0=π/2
На рисунке 2 и 3 изображены зависимости проигрыша l от отношения помеха-формирующий шум (q2) при разных значениях центральной частоты помехи и отношениях мощности сигнал-помеха, которые были получены из формулы (3) и в результате моделирования работы модельного компенсатора.
Анализируя график на рисунке 2, можно отметить, что чем выше центральная частота помехи, тем более чувствительным для снижения проигрыша является выбор значения отношения мощности помеха-формирующий шум в каналах. Аналогично при отношении мощности сигнал-помеха больше либо равно 1 выбор значения отношения мощности помеха-формирующий шум в каналах является критичным (см.рис.3).
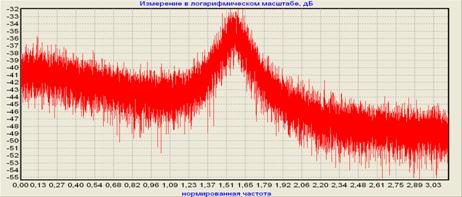
На рисунке 4 наглядно показаны результаты компенсации узкополосной помехи модельным компенсатором. В частности, при равных мощностях сигнала и помехи на входе, подавление УНП (измеренное по максимумам спектральных плотностей) составляет около 30дБ.
 а)
а)
 б)
б)
|
Рис.4. Спектральные плотности смеси сигнала и помехи (а), сигнала на выходе модельного компенсатора (б)
при q2=5дБ, α=0.7, β=0.1, η=0дБ, ω0= π/2
Выводы
1. Решена задача выделения гауссово-марковского процесса, действующего на фоне узкополосного нормального процесса двухканальным модельным компенсатором помех в условиях полной взаимной некоррелированности помех в каналах. При отношении мощности сигнал-помеха на входе 0 дБ компенсация помехи составляет около 30 дБ (рис.4).
2. Найдено аналитическое выражение проигрыша оптимальному винеровскому фильтру (ф.(8)), которое является верхней предельной оценкой отношения дисперсий ошибки фильтрации при малых значениях отношения мощности помеха-формирующий шум в каналах.
3. В ходе моделирования установлено, что существует оптимальное значение отношения мощности помеха-формирующий шум, при котором полный проигрыш минимален. При этом, чем выше центральная частота помехи, тем более чувствительным для снижения проигрыша является выбор значения отношения мощности помеха-формирующий шум в каналах (рис.2). Аналогично, при больших отношениях мощности сигнал-помеха (больше либо равно единице) выбор значения отношения мощности помеха-формирующий шум в каналах также является критичным (рис.3).
Литература
1. Манохин А.Е. Адаптивный компенсатор помех на основе формирования адаптивных моделей случайных процессов / А.Е.Манохин, Ю.А.Нифонтов // Журнал радиоэлектроники [Электронный ресурс]. – 2011.- №2. – Режим доступа: http://jre.cplire.ru/jre/feb11/6/text.html, свободный. – Загл. с экрана.
2. Шахтарин Б.И. Фильтры Винера и Калмана. –М: Гелиос АРВ, 2008. 408с.: ил.
3. Уидроу Б., Стирнз С. Адаптивная обработка сигналов. Пер. с англ. – М.:Радио и связь, 1989. – 440с.
 (1)
(1)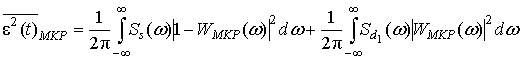 (3)
(3)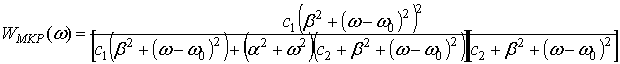 (4)
(4)