УДК 57.02.001.57

ВОССТАНОВЛЕНИЕ ПАРАМЕТРОВ РАДИОИМПУЛЬСА ЛАЗЕРНОГО ДОПЛЕРОВСКОГО АНЕМОМЕТРА

 

А. М. Шайдук, С. А. Останин

ГОУ ВПО «Алтайский государственный университет», г. Барнаул

Получена 28 октября 2011 г.

 

Аннотация. Предложен способ восстановления формы радиоимпульса из сложного сигнала лазерного доплеровского анемометра с большим количеством частиц в измерительном объеме. Способ основан на обратном преобразовании Фурье сигнала лазерного доплеровского анемометра и учете априорной информации о сигнале.

Ключевые слова: лазерный доплеровский анемометр, спектральный анализ, реконструкция сигнала.

Abstract. A method for reconstructing the shape of the radio pulse from the composite signal laser Doppler anemometer with a large number of particles in the measuring volume. The method is based on the inverse Fourier transform of the signal laser Doppler anemometer and a priori information about the signal.

Keywords: laser Doppler anemometer, spectral analysis, signal reconstruction.

 

В лазерной доплеровской анемометрии оптический сигнал, поступающий на фотодетектор, несет информацию о скорости, структурных и фазовых свойствах рассеивателей [1-2]. Если измерительный объем выбирают таким образом, чтобы вероятность появления в нем более чем одной частицы была минимальной, существует возможность измерения концентрации движущихся частиц. К таким измерителям относятся лазерные доплеровские анемометры, позволяющие определять скорость, счетную концентрацию и размеры аэрозольных частиц, проходящих через измерительный объем. В этом случае электрический сигнал на выходе фотодетектора имеет вид одиночного радиомпульса [3-4].

Естественным ограничением диапазона измеряемых концентраций частиц, для этого способа, является величина измерительного объема . Концентрация частиц  в потоке может быть измерена, если она не превышает величину . В настоящей работе обсуждается возможность извлечения из сигнала информации о параметрах радиоимпульса лазерного анемометра при концентрациях, больших чем _, с целью оценки концентрации и скорости частиц.

Рассмотрим модель сигнала фотодетектора, которая представляет  собой  суперпозицию  одиночных  радиоимпульсов вида

 

,                                 (1)

 

последовательно следующих друг за другом через  некоторый интервал времени :

 

.                                          (2)

 

Константа  в выражении (1) определяет полуширину огибающей радиоимпульса,  – частота доплеровского сдвига,  – число радиоимпульсов в выражении (2). Величина интервала времени  определяется  концентрацией частиц в потоке, а частота доплеровского сдвига  – скоростью частиц. Вид функций  и   представлен на рисунках 1 и 2 соответственно.

 

 

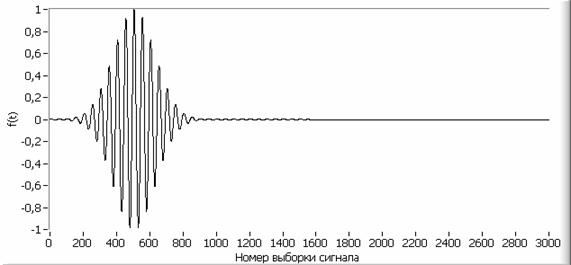
Рис. 1. Результат моделирования функции .

 

 

 

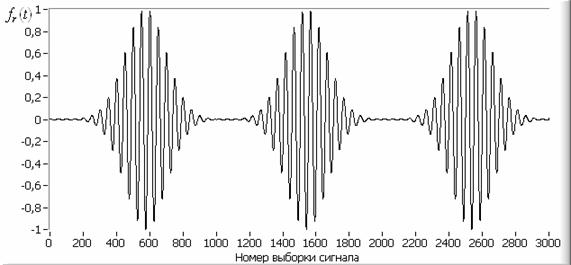
Рис. 2. Результат моделирования функции .

        

Поскольку в измерительный объем частицы влетают в различные точки сечения измерительного объема независимо, будем считать, что в каждую точку сечения последовательность частиц влетает со сдвигом по времени . Величина  является случайной величиной и описывается статистической плотностью распределения. Следовательно, результирующий сигнал , с учетом вкладов всех последовательностей частиц, влетающих в измерительный объем, можно записать как

,                                                (3)

 

где  – реализация случайного сдвига,  – количество последовательностей. Результат численного моделирования одной реализации сигнала  показан на рисунке 3.

 

 

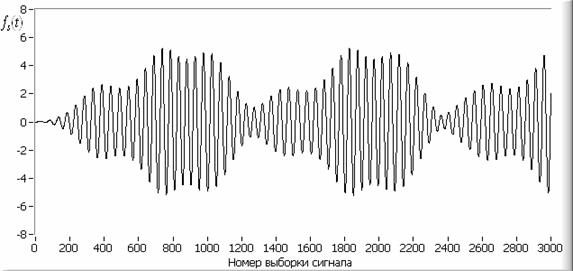
Рис. 3. Результат моделирования функции . Значение сдвига  распределено равномерно, в диапазоне от 0 до .

 

Спектр функции типа (3) получен в работе [5]:

 

                            (4)

 

где  – спектральная мощность сигнала, – комплексная спектральная функция,  – сопряженная спектральная функция,  – спектр одиночного радиоимпульса,  – спектр дельта-функций,  – компонента, отражающая случайный сдвиг фаз последовательностей радиоимпульсов.

Покажем возможность  восстановления некоторых параметров радиоимпульсов, если известна спектральная мощность  . Если известна спектральная функция  регистрируемого сигнала  , последний может быть восстановлен с помощью обратного преобразования Фурье. Однако, практическое выполнение этой процедуры связано со следующими проблемами:

1.    Спектральные анализаторы обычно измеряют спектральную мощность , а не функцию . Кроме того, измерение возможно на ограниченном интервале значений .

2.    Спектральная функция  является комплексной. Задача восстановления действительной и мнимой части  функции  по ее спектральной мощности требует решения уравнения

 

.                  (5)

 

Решение этого уравнения невозможно без дополнительных гипотез о поведении комплексной функции .

3.    Действительная и мнимая части спектральной функции  являются чрезвычайно быстро осциллирующими функциями, в которых содержится информация о поведении радиоимпульсов. Вид функции меняется даже при изменении начала отсчета времени при регистрации радиоимпульсов. Часть этой информации не представляет интереса при оценки формы радиоимпульсов и частоты из следования и вполне может быть не использована.

Частоту следования радиоимпульсов можно восстановить, анализируя тонкую структуру спектра сигнала . Как следует из анализа математической модели подобного сигнала [5] и элементарных свойств преобразования Фурье, в случае, когда частота следования радиоимпульсов постоянна, спектр представляет собой набор эквидистантно расположенных спектральных линий, расстояние между которыми равно частоте следования радиоимпульсов. Существует ряд причин, на которых мы остановимся ниже, по которым  тонкая структура  реального сигнала может не наблюдаться, что приведет к невозможности определения частоты следования отдельных радиоимпульсов.

Из результатов анализа математической модели [5] следует, что огибающая спектра  определяется спектральной мощностью одного радиоимпульса. Поэтому параметры огибающей содержат часть информации о свойствах спектра одного радиоимпульса, вид которого, в общем случае, нам неизвестен. В частности, длительность одного радиоимпульса можно оценить из соотношения неопределенности

,

где   - характерная ширина огибающей спектра.

Реальная часть спектра функции (1) близка к нулю, поэтому уравнение (5) решается относительно мнимой части неизвестного спектра радиоимпульса , поскольку функция  восстанавливается по огибающей спектра

 

                                            (6).

 

Заметим, что модельный сигнал имеет спектр, огибающая которого носит случайный характер (рисунок 4) и получить информацию о параметрах одного радиоимпульса проблематично. Однако, следует отметить, что спектр, представленный на рисунке 4, получен от одной реализации сигнала  .

 

 

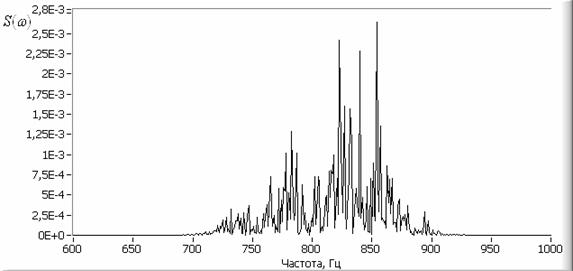
Рис. 4. Спектр модельного сигнала . Коэффициент вариации интервала следования радиоимпульсов .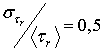

 

  

 

Рис. 5. Спектр мощности _, усредненный по случайным  реализациям сигнала  _, при коэффициенте вариации интервала следования радиоимпульсов 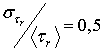. Спектр мощности  - при .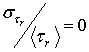

 

Численное моделирование, проведенное нами, показало, что усредненный по случайным  реализациям сигнала   спектр мощности  приближается с увеличением количества реализаций к спектру мощности одной последовательности радиоимпульсов (рисунок 5). Спектр одного радиоимпульса теперь может быть приблизительно оценен с помощью соотношения (6), только под функцией  нужно понимать функцию, усредненную по множеству реализаций сигнала .

Восстановление параметров радиоимпульса из модельного сигнала  было выполнено в среде LabVIEW. При моделировании использовалось нормальная плотность распределения периода следования радиоимпульсов . Программа позволяла устанавливать произвольное значение дисперсии периода следования . Результаты  восстановления показаны на рисунке 6.

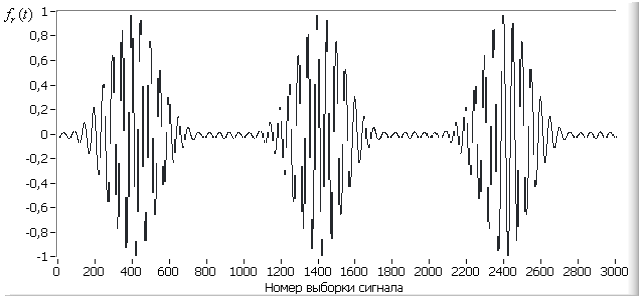
На рисунке  6-а показан восстановленный сигнал при коэффициенте вариации интервала радиоимпульсов _, равном 0,5. Из рисунка видно, что восстанавливается функция  типа (1) . На рисунке  6-б показан восстановленный сигнал при нулевом коэффициенте вариации (периодическое следование радиоимпульсов в последовательности при случайном сдвиге разных последовательностей). Восстанавливается функция  типа (2) .

 

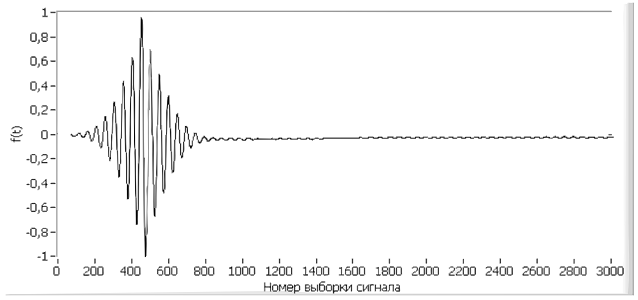
а

б

Рис. 6. а - результат восстановления функции , 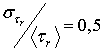; б - результат восстановления функции , .

 

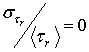Частота доплеровского сдвига  оценивалась по первому максимуму автокорреляционной функции восстановленного сигнала. Относительная погрешность оценки частоты доплеровского сдвига  составила  0,005  при коэффициенте вариации интервала следования радиоимпульсов 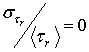 и 0,01 при 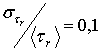. Интервал следования радиоимпульсов  оценивался по автокорреляционной функции восстановленного сигнала  (рисунок 6-б). Относительная погрешность оценки математического ожидания интервала   составила  0,007  при 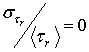 и 0,04 при .

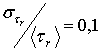Полученные результаты показывают принципиальную возможность выполнять оценки скорости движения частиц по доплеровской частоте   и концентрации частиц в потоке по интервалу времени , восстановленным из спектра сигнала лазерного доплеровского анемометра, в измерительном объеме которого находится более одной частицы.

 

Литература

 

1.   Дубнищев Ю.Н., Ринкевичюс Б.С. Методы лазерной доплеровской анемометрии. М.: Наука. 1982. 303 с.

2.   Ринкевичюс  Б.С.  Лазерная  диагностика  потоков /  Под  ред. Фабриканта В.А. М.: Изд-во МЭИ. 1990. 298 с.

3.   Дубнищев Ю.Н., Павлов В.А. Лазерный метод измерения размера частиц // Квантовая электроника. – 1996.– №11.– С. 1051-1055.

4.   Бураков С.Д., Годлевский А.П., Останин С.А. Определение микрофизических параметров аэрозоля приемопередатчиком на основе твердотельного лазера. // Оптика атмосферы.– 1989.– №2.– С. 206-210.

5.   Шайдук А.М., Останин С.А. Моделирование электромиографического сигнала средствами LabVIEW. // Известия Алтайского государственного университета. – Барнаул: Изд.-во АлтГУ – Ч.1(65), 2010. – С. 195-201.