Линейный отклик квантовой проволоки с объемными контактами
С. Н. Артеменко 1,2, В. Г. Корнич 2 , Д. С. Шапиро 1
1 Институт радиотехники и электроники им. В.А.Котельникова РАН
2 Московский физико-технический институт
Получена 3 ноября 2011 г.
Аннотация: Вычислена частотная зависимость импеданса квантовых проволок, подсоединенных к объемным контактам, близких к идеальным адиабатическим. Исследовано влияние межэлектронного взаимодействия на импеданс. Показано, что в случае неадиабатических контактов, низкочастотный линейный отклик сильно подавляется фриделевскими осцилляциями вблизи контактов.
Ключевые слова: квантовая проволока, импеданс, взаимодействие между электронами.
Abstract. Frequency dependent impedance of quantum wires with bulk nearly ideal adiabatic contacts is calculated. Effect of inter-electric interaction on the impedance is studied.
Key words: quantum wire, impedance, electron-electron interaction.
1. Введение
Интерес к одномерным (1D) проводникам (мы их для простоты
будем называть общим термином «квантовые проволоки») связан как с тенденцией
миниатюризации электронных приборов, сопровождающейся переходом к нанометровым
размерам элементов, так и с качественно новыми физическими характеристиками,
возникающими из-за межэлектронного взаимодействия. Примерами 1D проводников являются
полупроводниковые квантовые проволоки [1], одиночные проводящие цепочки атомов
на поверхности полупроводников [2], углеродные нанотрубки [3], графеновые
полоски нанометровой ширины и др. Межэлектронное взаимодействие в 2D и 3D материалах, как правило, описывается в рамках теории
ферми-жидкости, в которой элементарными возбуждения являются ферми-частицы —
электроны и дырки. А к 1D
проводникам подходы, основанные на представлениях ферми-жидкости, неприменимы,
поэтому их свойства часто описывают в приближении жидкости Латтинджера, которую
можно представить себе как одномерный аналог вигнеровского кристалла (см. книгу
[4]). Элементарными возбуждениями в жидкости Латтинджера являются не фермионы,
а колебания зарядовой или спиновой плотности со статистикой Бозе. В результате
оказывается, что процессы переноса тока и заряда в 1D системах обладают рядом особенностей, не встречающихся в
объемных материалах. Экспериментальные подтверждения подобного поведения
наблюдались во многих 1D системах,
в частности, в полупроводниковых квантовых проводах [1,
5] и углеродных
нанотрубках [3]. В 1D системах с
межэлектронным отталкиванием проводимость сильно подавляется даже единственной
примесью, что выражается в степенной зависимости проводимости от напряжения
и/или температуры [6-8]. А в недавней теоретической работе [9] был предсказан
динамический режим, при котором протекание постоянного тока сопровождается
генерацией колебаний с частотой 
, где 
- постоянный ток. Сильное влияние
примеси на проводимость связано с движением фриделевских осцилляций при
протекании постоянного тока. Формирование фриделевских осцилляций происходит и
на резких, не адиабатических, контактах 1D системы взаимодействующих электронов с 2D или 3D электродами. Задача о протекании тока через контакт 1D электронов в коррелированном
состоянии, которое описывается как жидкость Латтинджера, и электродами более
высокой размерности, в которых электроны образуют ферми-жидкость, изучалась в
работе [10], где были выведены граничные условия для неадиабатических контактов
и было показано, что в этом случае у контакта возникают фриделевские
осцилляции, которые подавляют омическую проводимость, что как и в случае
примеси [9], приводит к динамическому режиму проводимости, напоминающему эффект
Джозефсона и кулоновскую блокаду.
Очевидно, что
межэлектронное взаимодействие и наличие фриделевских осцилляций у контакта
должно повлиять и на частотную зависимость импеданса квантовых проволок, не
содержащих дефектов. Частотная зависимость импеданса чистых квантовых проволок
с короткодействующим межэлектронным взаимодействием изучалась в работах
[11-13], где было установлено, что, в отличие от проводимости на постоянном
токе, импеданс зависит от параметров межэлектронного взаимодействия внутри
квантовой проволоки и на его частотную зависимость влияют резонансы, связанные
с отражением бозонных возбуждений от конца проволоки. Авторы цитированных работ
считали, что ток в проволоке вызывается электрическим полем 
, распределенным по всей длине проволоки. Поэтому было
получено, что импеданс увеличивался с увеличением длины квантовой проволоки,
что сильно отличается от статического случая, когда проводимость оказывается
равна кванту проводимости и не зависит от длины проволоки. Это связано с тем,
что разность потенциалов, приложенная к электродам, подводящим ток, падает на
сужении объемных электродов в месте присоединения квантовой проволоки, а ток
внутри проволоки, не содержащей примесей, возникает в результате инжекции зарядов
из контактов и, следовательно, должен описываться граничными условиями, как это
было показано в работах Эггера и Граберта [14]. Такая постановка задачи
становится очевидной при достаточно низких частотах, когда внешнее
электрическое поле, если бы оно существовало внутри проволоки, вызывало бы
ускорение электронов в идеальной проволоке без примесей и перераспределение
зарядов до тех пор, пока не установится такое стационарное состояние, при
котором падение напряжения происходит в области контактов, а не внутри
проволоки. И такие рассуждения можно применить вплоть до частот порядка
плазменной частоты или частоты диэлектрической релаксации (обратного
максвелловского времени) в контактах. Но возможна и ситуация, когда ток в
квантовой проволоке вызывается электрическим полем, распределенным по всей
длине проволоки. Так будет, если квантовая проволока помещена, например, в
резонатор, в область, где электрическое поле параллельно квантовой проволоке,
или на проволоку падает электромагнитное излучение. При этом величина импеданса
и его частотная зависимость будут зависеть от того, подсоединена ли проволока к
контактам.
В этой работе мы
рассчитываем частотную зависимость импеданса квантовой проволоки в случае,
когда ток вызван переменными потенциалами 
, приложенными к объемным контактам,
а также рассматриваем линейный отклик на внешнее электрическое поле 
, распределенное по всей длине квантовой проволоки.
При этом мы рассмотрим как случай короткодействующего межэлектронного
взаимодействия, которое возникает при наличии металлического затвора,
расположенного вблизи проволоки и приводящего к экранированию кулоновского
дальнодействия, так и случай дальнодействующего кулоновского взаимодействия.
Основное отличие нашей работы от предыдущих исследований [11-13] состоит в том,
что мы на границе проволоки используем граничные условия для контакта квантовой
проволоки с массивными электродами, рассматриваем не только случай
короткодействующего экранированного электрон-электронного взаимодействия, но и дальнодействующего,
а также вычисляем отклик не только на разность потенциалов, но и на средний
потенциал, возникающий при приложении к обоим контактам одинакового переменного
напряжения, приводящего к инжекции зарядов в квантовую проволоку.
Ниже мы будем считать
и
равными единице, возвращаясь к размерным единицам,
где это необходимо, в конечных формулах.
2. Основные уравнения
Мы рассматриваем систему,
состоящую из одномерного проводника (квантового провода) длиной 
Межэлектронное взаимодействие описывается в рамках
модели Томонаги-Латтинджера (ТЛ), в которой делается переход от фермионных
полевых операторов к бозонному фазовому полю смещения 
и сопряженному оператору плотности импульса 
Возмущения плотности заряда и ток выражаются через с помощью соотношений
В случае кулоновского взаимодействия между электронами бозонизованный гамильтониан ТЛ имеет вид
здесь
,
где второе слагаемое учитывает
потенциал кулоновского взаимодействия электронов (
диэлектрическая проницаемость окружающей среды).
Первая строка в гамильтониане относится к спиновому, а вторая - к зарядовому
каналу. В случае короткодействующего взаимодействия, которое возникает
вследствие экранирования кулоновского взаимодействия затвором, функцию 
надо заменить на 
в результате чего получится стандартный гамильтониан
ТЛ. Мы будем рассматривать случай, когда электроны отталкиваются и сила
взаимодействия не зависит от спина, в этом случае параметры взаимодействия 
а 
Мы будем для краткости, в основном, рассматривать
близкодействие, приводя результаты для дальнодействия без вывода. Кроме того мы
будем выводить результаты без учета спиновых степеней свободы, рассматривая
бесспиновые (спин-поляризованные) электроны, а в конце отметим отличия,
которые возникают с учетом спиновых степеней свободы.
Если квантовая проволока
находится во внешнем переменном поле, например, параллельном проволоке
электрическом поле падающей волны, то к гамильтониану взаимодействующих
электронов (2) надо добавить потенциальную энергию электронов во внешнем
электрическом потенциале
,
где в качестве плотности заряда стоит первый член в (1), описывающий плавную компоненту плотности.
Мы будем решать уравнения
движения для гейзенберговских операторов 
которые имеют вид волнового уравнения
где 
- скорость плазменных волн, а 
- внешнее электрическое поле.
В качестве граничного условия на контактах мы воспользуемся операторными граничными условиями (ГУ), полученными в работе [10]
где последнее слагаемое в левой части
описывает влияние фриделевской осцилляции, 
-численный коэффициент, величина которого 
если прозрачность барьера не близка к единице, и 
при 
причем мы будем рассматривать именно этот случай
контактов, достаточно близких к идеальным. Таким образом, фриделевские
осцилляции, как и должно быть, исчезают, если контакты адиабатические. В правой
части стоят источники, пропорциональные операторам избыточной плотности заряда,
в правом (R) и левом (L)
электродах, соответственно. В случае дальнодействия фактор 
в знаменателе (4), учитывающий экранирующее действие
затвора, надо заменить на единицу.
Электрический ток в
квантовой проволоке выражается через термодинамическое среднее от поля
смещения, 
, в то время как сам полевой оператор
содержит еще и флуктуирующую часть, 
, а флуктуации, как известно, в 1D проводниках очень велики. Нам будет
удобно выделить термодинамическое среднее в явном виде, представив полный
оператор поля смещения в виде 
. Тогда, учтя, что среднее от
источников определяется потенциалами электродов 
, соответственно, ГУ для средних приобретут вид
В случае идеальных адиабатических контактов эти условия сводятся к полученным Эггером и Грабертом [14].
Корреляционные функции для флуктуирующих частей коммутатора и антикоммутатора одинаковы для обоих электродов (корреляции между флуктуациями в левом и правом электроде отсутствуют) и в частотном представлении имеют вид
Так как мы решаем задачу
о линейном отклике, мы должны линеаризовать граничные условия по величине
термодинамического среднего фазы . При этом основные трудности возникают с нелинейным
слагаемым с косинусом в граничных условиях, поскольку полевой оператор содержит
как термодинамически среднюю часть, так и флуктуирующую, 
В результате линеаризации граничных
условий (5) по 
и перехода к преобразованию Фурье по времени мы получаем граничные
условия
При этом мы выбрали в качестве
равновесных значений среднего фазового оператора на границе проволоки такие
величины, которые соответствуют устойчивому состоянию системы, и отсчитываем
возмущения 
от этих значений. Новая характерная
энергия 
описывает перенормировку
коэффициентов 
описывающих влияние одномерных
флуктуаций на среднее значение амплитуды фриделевских осцилляций. Для
вычисления флуктуаций надо решать уравнения движения для
а для вычисления среднего квадрата флуктуаций мы
воспользуемся гауссовой моделью, как это было показано в работе [10]. В общем
случае несимметричных контактов вычисления оказываются довольно громоздкими,
поэтому мы ограничимся случаем одинаковых контактов и случаем, когда один из
контактов оборван.
3. Линейный отклик на напряжение, приложенное к контактам
В этом разделе мы считаем, что
внешнее поле 
и правая часть уравнения движения
(3) равна нулю.
3.1. Короткодействующее взаимодействие между электронами
Сначала рассмотрим случай
одинаковых контактов 
. Тогда, согласно результатам работы [10] средний
квадрат флуктуаций фазы на контактах различен в разных предельных случаях. При
низких температурах 
и в случае, когда длина квантового провода достаточно
велика, 
мы получим с логарифмической
точностью
Из формулы (8) следует, что влияние
фриделевских осцилляций сохраняется лишь при конечной величине межэлектронного
взаимодействия, то есть при 
а при
то есть в пренебрежении межэлектронным
взаимодействием 
В противоположном
предельном случае, когда либо велика температура, 
либо мала длина проволоки
, флуктуации оказываются очень велики и влиянием
фриделевских осцилляций можно пренебречь, положив
Решая теперь уравнение
для термодинамически усредненной части фазы с граничными условиями (7), мы
найдем значения фаз 
вблизи контакта и с помощью формулы (1) вычислим ток
вблизи контактов. Для отклика на частоте 
получим
где 
- квант проводимости.
Итак, мы получили, что на
конечной частоте через противоположные контакты к проволоке может течь разный
ток, а на нулевой частоте ток через оба контакта одинаков. Это связано с тем,
что если к обоим контактам приложить одинаковый переменный потенциал 
, заряды будут попеременно втекать и вытекать из
проволоки, иными словами, контакты будут действовать как затвор, создающий
емкостной ток. А разность потенциалов 
дает вклад в ток, который, как и должно быть,
оказывается одинаковым на обоих контактах. В случае неидеальных контактов
импедансы обращаются в бесконечность при стремлении частоты к нулю, что связано
с подавлением проводимости фриделевскими осцилляциями [10]. В случае идеальных
адиабатических контактов, а также при высоких температурах, 
, и в коротких проволоках, 
величина 
характеризующая влияние фриделевских осцилляций,
обращается в ноль. Поэтому в пределе низких частот импеданс 
определяется квантом проводимости, а 
Осцилляции импедансов (10) связаны с многократными отражениями возбуждений в квантовой проволоке от контактов, причем отражения возникают даже в случае идеальных адиабатических контактов из-за того, что в нашей модели имеется резкая граница между областями взаимодействующих электронов в квантовой проволоке и невзаимодействующих электронов в объемных электродах. Отметим, что в реальной экспериментальной ситуации такая граница может быть размыта, что поведет к размыванию осцилляций.
Рассмотрим теперь другую
схему присоединения контактов к квантовой проволоке, когда контакт к квантовой
проволоке при 
отсутствует и вычислим ток при 
. Решение в этом случае аналогично предыдущему случаю,
единственное различие состоит в том, что нужно использовать другое граничное
условие для оборванного контакта. Для такого контакта в качестве граничного
условия мы потребуем обращения тока на контакте в ноль, что на конечных
частотах означает условие обращения в ноль и фазового оператора. В результате
вычисления мы получим, что ток через контакт при будет равен
Мы видим, что в этом случае через контакт может течь только ток, связанный с процессами зарядки проволоки, который обращается в ноль на нулевой частоте.
3.2. Дальнодействующее взаимодействие между электронами
В случае
дальнодействующего взаимодействия между электронами, то есть в отсутствие
экранирующего затвора, решение уравнений движения (3) в случае
дальнодействующего взаимодействия оказывается более трудоемким и длинным,
поэтому мы приведем результат без вывода. Отметим только, что в этом случае
уравнения движения для гайзенберговских операторов оказываются интегральными
уравнениями по координате, причем на потенциал взаимодействия между электродами
в проводе оказывает влияние экранирующее действия электродов - подводящих
токовых контактов. Поэтому мы провели расчет для определенной геометрии, в
которой длина проволоки полагается меньше размеров электродов, образующих
конденсатор, пластины которого соединены одномерным проводником. Тогда
электроды можно рассматривать как бесконечные металлические пластины и
описывать их экранирующее действие с помощью сил изображения. В этом случае
удается решить уравнения с помощью разложения в ряд Фурье по координате. В
результате решения оказывается, что перенормировка коэффициента флуктуациями играет значительно меньшую роль. Дело в
том, что параметр 
, определяющий величину взаимодействия, порядка
постоянной тонкой структуры, в которой скорость света заменена на фермиевскую
скорость,
поэтому средний квадрат флуктуаций оказывается небольшим даже при умеренной величине взаимодействия, соответствующей вполне реалистичным соотношениям параметров, поскольку условие малости флуктуаций при дальнодействии приобретает вид
где 
измеряется в единицах 
см/сек. Таким образом во многих случаях можно
пренебречь влиянием флуктуаций на перенормировку коэффициентов в (7).
В результате решения уравнений
движения для средней фазы мы находим выражение для тока
где
,
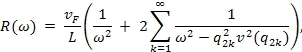
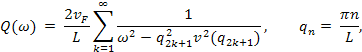
а 
- скорость плазменных возбуждений в
системе с кулоновским дальнодействием. Здесь 
- диаметр квантовой проволоки, который является малой
величиной порядка фермиевской длины волны.
Рассмотрим сначала
симметричные контакты . В этом случае
Эти выражения упрощаются в предельных
случаях больших и малых частот. При низких частотах, 
, получим
При увеличении частоты в импедансе
появится осциллирующая часть, связанная с обращением знаменателей в 
и 
в ноль, когда на длине проволоки укладывается целое
число длин волн плазменных возбуждений. А в пределе больших частот, 
, с логарифмической точностью получим
В другой схеме
присоединения контактов к квантовой проволоке, когда контакт к квантовой
проволоке при отсутствует и вычисляется ток при 
, получим
где в пределе низких частот импеданс
стремится к бесконечности, а при больших частотах 
импеданс 
описывающий действие контакта в качестве затвора,
изменяющего заряд проволоки, оказывается похожим на результат в случае двух
контактов, присоединенных к концам проволоки.
Основное отличие от случая
короткодействующего взаимодействия между электронами состоит в том, что вместо
фактора влияние межэлектронного
взаимодействия на линейный отклик определяется длинноволновой частью
кулоновского потенциала, в результате чего в формулах появляются большие
логарифмы, зависящие от частоты.
4. Линейный отклик на внешнее электрическое поле
В этом разделе мы будем
искать отклик на внешнее переменное электрическое поле 
стоящее в правой части уравнения движения (3). При
этом мы предполагаем, что поле не зависит от координат и вся проволока
находится в области поля. Когда проволока подключена к контактам, токи,
вызванные внешним электрическим током, могут через контакты затекать и во
внешнюю электрическую цепь, что приведет к образованию на подводящих контактах
потенциалов, определяющихся импедансами внешней цепи, 
Эти потенциалы нужно учесть в граничных условиях, и
они дадут вклад в ток, который вычислялся в предыдущих разделах статьи. Так как
мы решаем линейную задачу, то суммарный ток будет определяться суммой двух
независимых вкладов, вклада от поля (с нулевыми потенциалами в граничных условиях (5) и
вклада от напряжения на контактах (с нулем в правой части уравнения движения
(3)). Поскольку второй случай фактически сводится к результатам предыдущего
раздела, ниже мы будем использовать граничные условия (5) с нулевой правой
частью.
4.1. Короткодействующее взаимодействие между электронами
В этом разделе мы снова
начнем с симметричного случая, когда квантовая проволока присоединена к
одинаковым контактам. Мы снова решаем уравнение для термодинамически
усредненной части фазы, но теперь с полем в правой части, и с нулевыми граничными условиями (7)
и находим значения фаз вблизи контакта, а затем с помощью формулы (1)
вычисляем ток вблизи контактов. Для отклика на частоте 
получим
где мы ввели обозначение
. Cогласно (14) получается, что при достаточно больших
частотах импеданс растет с увеличением длины проволоки и только в пределе малых
частот, 
зависимость импеданса от длины
исчезает
причем импеданс зависит от параметра
межэлектронного взаимодействия даже в случае адиабатических контактов, когда
фриделевские осцилляции не подавляют проводимость 
Если контакт к квантовой
проволоке при отсутствует и 
, для тока через контакт при мы получим
В пределе низких частот, как и
следовало ожидать, 
.
4.2. Дальнодействующее взаимодействие между электронами
В случае дальнодействия
мы снова рассматриваем случай, когда параметр 
не мал по сравнению с единицей, в результате чего
кулоновское дальнодействие подавляет одномерные флуктуации.
В симметричном случае 
мы получаем для тока
где снова 
и при достаточно больших частотах импеданс растет с
увеличением длины проволоки и только в пределе малых частот, 
, зависимость импеданса от длины исчезает
При повышении частоты импеданс
осциллирует из-за отражений возбуждений от контактов и в пределе больших
частот, , мы с логарифмической точностью
получим
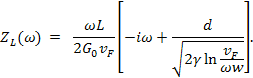
Когда контакт к квантовой проволоке при 
отсутствует и вычисляется ток при , мы получим
В пределе низких частот,
как и в случае короткодействующего взаимодействия, получается . А при увеличении частоты импеданс, проходя через
осцилляции, стремится при 
к
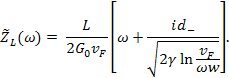
5. Заключение
Обсудим прежде всего, к
каким изменениям приведет учет спиновых степеней свободы. В целом, частотные
зависимости импедансов во всех рассмотренных случаях оказываются практически
аналогичными. Основное отличие от бесспиновой системы состоит в том, что из-за
наличия электронов с разными направлениями спина в формулах для импедансов
квант проводимости 
нужно умножить на 2, а спиновые флуктуации уменьшат
величину в результате чего в формуле (8) под 
надо понимать величину
.
Мы получили, что взаимодействие 1D электронов сильно влияет на линейный отклик квантовой проволоки на высокочастотное электрическое поле. Это влияние особенно велико в случае, если квантовая проволока присоединена к контактам, которые отличаются от идеальных адиабатических. Еще одной интересной особенностью рассматриваемой системы является то, что межэлектронное взаимодействие сильно влияет не только на отклик ситемы на разность потенциалов, приложенных к контактам, а также на отклик, возникающий при приложении к обоим контактам одинакового переменного напряжения, приводящего к инжекции зарядов в квантовую проволоку.
Частотная дисперсия
импеданса определяется двумя характерными частотами. Первая, 
, определяется длиной проволоки и скоростью плазменных
волн, которая в случае короткодействия равна 
и может в несколько раз превышать фермиевскую
скорость и быть значительно больше в системе с дальнодействием, где 
Если воспользоваться данными из экспериментальной
работы [5], где длина квантовой проволоки была 17 мкм, а скорость 
, мы получим оценку 
, а если взять длину проволоки 
из работы [15], то с той же
величиной скорости получится 
. Таким образом эта частота может меняться в широких
пределах. Вторая характерная частота определяется величиной фриделевской
осцилляции у контакта и также может меняться в широких пределах, от нуля в
идеальных адиабатических контактах до довольно большой величины, попадающей в
терагерцовый диапазон частот, в зависимости от степени отклонения контакта от
адиабатичности.
Работа поддержана грантом Министерства образования и науки РФ (контракт № 16.513.11.3066). ВГК и ДСШ благодарят за поддержку Фонд некоммерческих программ "Династия".
Литература
[1] O.M.Auslaender, H.Steinberg, A.Yacoby et al, Science 308, 88 (2005).
[2] H. W. Yeom , Y. K. Kim, E. Y. Lee, K.-D. Ryang, and P. G. Kang, Phys. Rev. Lett. 95, 205504 (2005).
[3] H. Ishii, H. Kataura, H. Shiozawa et al., Nature 426, 540 (2003).
[4] T. Giamarchi, Quantum Physics in One Dimension, (Clarendon Press, Oxford, 2003).
[5] Y. Jompol, C. J. B. Ford, J. P. Griffiths, I. Farrer, G. A. C. Jones, D. Anderson, D. A. Ritchie, T. W. Silk, A. J. Schofield, Science 325, 597 (2009).
[6] C. L. Kane and M.P.A. Fisher, Phys. Rev. Lett. 68, 1220 (1992).
[7] K. A. Matveev and L. I. Glazman, Phys. Rev. Lett. 70, 990 (1993).
[8] A. Furusaki and N. Nagaosa, Phys. Rev. B 47, 4631 (1993).
[9] S. N. Artemenko, S. V. Remizov, D. S. Shapiro, Письма в ЖЭТФ 87, 792 (2009).
[10] С.Н. Артеменко, П.П. Асеев, Д.С. Шапиро, Письма в ЖЭТФ, 91, 659 (2010).
[11] V. V. Ponomarenko, Phys. Rev. B 54, 10328 (1996).
[12] В.А. Сабликов, Б.С. Щамхалова, Письма в ЖЭТФ, 66, 40 (1997).
[13] K. V. Pham, Eur. Phys. J. B, 36, 607 (2003).
[14] R. Egger, H. Grabert, Phys. Rev. Lett. 80, 2255 (1998); Phys. Rev. B 58, 10761 (1998).
[15] Д. А. Козлов, З. Д. Квон, А. Е. Плотников, Д. В. Щеглов, А. В. Латышев Письма в ЖЭТФ, 86, 752 (2007).