УДК 621.391
ОБНАРУЖЕНИЕ СИГНАЛОВ ПО КОРРЕЛЯЦИИ ОРТОГОНАЛЬНО-ПОЛЯРИЗОВАННЫХ КОМПОНЕНТ
А. В. Болдин, В. Л. Румянцев, А. В. Хомяков
ОАО Центральное конструкторское бюро аппаратостроения, г. Тула
Получена 26 октября 2011 г.
Аннотация. Определено решающее правило обнаружения цели на фоне гауссовской помехи по корреляции ортогонально-поляризованных компонент. Синтезированы устройства оптимального и адаптивного обнаружения цели, проведена сравнительная оценка их эффективности.
Ключевые слова: обнаружение цели, радиолокационный сигнал, поляризационные параметры, отношение правдоподобия, коэффициент корреляции.
Abstract. The decision rule for detecting a target at the background of Gaussian noise by correlation of orthogonal polarized components has been determined. Devices for optimum and adaptive detection of targets have been synthesized; comparative etimate of their efficiency has been carried out.
Keywords: detection of a target, a radar signal, polarization parameters, likelihood ratio, correlation coefficient.
Введение
Вопросам радиолокационного обнаружения различных целей на фоне подстилающей поверхности посвящено значительное число работ [1-3]. Движение указанных целей приводит к преобразованию спектра зондирующего сигнала вследствие эффекта Доплера. Помимо эффекта Доплера к изменению спектра приводит и наличие вращающихся и вибрирующих элементов целей, а также наличие элементов с нелинейными характеристиками на их поверхности.
Технически задача выделения движущихся целей решается достаточно просто с помощью доплеровской фильтрации. Отсутствие доплеровских составляющих в спектре радиолокационного сигнала, отраженного от цели, приводит к необходимости использования для обнаружения поляризационных различий сигналов.
Анализ экспериментальных результатов [2,4] свидетельствует о высокой информативности коэффициентов корреляции ортогонально поляризованных компонент (ОПК) отраженного сигнала для селекции неподвижных целей. Повысить качество обнаружения возможно также уменьшив состояние неопределенности в приемнике, обусловленное вероятностным характером априорной информации о цели, применением процедуры адаптации. Так как адаптация в общем случае усложняет приемное устройство важно определить максимальное повышение качества обнаружения, которое можно ожидать при ее применении. Целью работы является синтез адаптивного алгоритма обнаружения сигналов, отраженных от целей, и сравнение его эффективности с оптимальным.
Принимаемая
двухканальным по поляризации приемником в общем случае случайно
поляризованная волна может быть представлена в произвольном
ортонормированном базисе ![]() в виде суперпозиции двух
ортогонально поляризованных компонент
в виде суперпозиции двух
ортогонально поляризованных компонент
где ![]() ; n - число наблюдаемых значений ОПК в каждом j-ом элементе
дальности.
; n - число наблюдаемых значений ОПК в каждом j-ом элементе
дальности.
Компоненты вектора Е вследствие влияния многих независимых факторов будем считать гауссовскими случайными процессами с параметрами Е1, E2, σ1, σ2.
Входящие в (1) компоненты считаются узкополосными со
средней частотой w0. Длина интервала наблюдения Т=пΔ удовлетворяет
неравенству ![]() ; Δ - интервал дискретизации случайного
процесса; коэффициент междупериодной корреляции близок к нулю;
корреляция между i-ми отсчетами ОПК в соседних элементах дальности
отсутствует.
; Δ - интервал дискретизации случайного
процесса; коэффициент междупериодной корреляции близок к нулю;
корреляция между i-ми отсчетами ОПК в соседних элементах дальности
отсутствует.
Выборочный коэффициент корреляции ОПК в j-ом периоде наблюдения оценивается по соотношению [5]
При указанных предположениях закон распределения величины rj можно записать в следующей форме
где ρ
- коэффициент корреляции в генеральной совокупности; 2F1 -гипергеометрическая функция; ![]() - номер элемента дальности.
- номер элемента дальности.
Оценка эффективности обнаружения цели оптимальным приемником
Пусть для принятых в интервале [0,Т] данных Е(ti) можно высказать две взаимно исключающие гипотезы: гипотеза H1, , что в j -ом элементе дальности наблюдается цель, и гипотеза H2, что имеется сигнал от фона.
Тогда задача обнаружения неподвижной цели может быть решена в рамках статистической теории проверки гипотез - как задача распознавания двух классов целей: N1 – наблюдаемая цель, N2 - подстилающая поверхность.
При использовании байесовского критерия
качества оптимальный не адаптивный приемник формирует на выходе величину,
пропорциональную отношению правдоподобия ![]() (E), и сравнивает ее с порогом L,
зависящим от матрицы выигрыша и потерь при решениях, а также от априорной
функции плотности вероятности параметра ρ:
(E), и сравнивает ее с порогом L,
зависящим от матрицы выигрыша и потерь при решениях, а также от априорной
функции плотности вероятности параметра ρ:
Осуществив подстановку (3) в (4), нетрудно получить алгоритм распознавания цели в виде
где ![]() .
.
Устройство, реализующее алгоритм (5), может быть в общем случае т - канальным, где т - число просматриваемых элементов дальности. После вычисления rji в соответствии с соотношением (2), для каждого j-го элемента дальности, нелинейной обработки полученной величины, осуществляется накопление результата по и периодам обзора и сравнение его с порогом, зависящим от априорных сведений, относительно параметров распределения (3).
Определим эффективность распознавания при использовании не адаптивного решающего правила (4). Эффективность распознавания удобно оценивать по величине ошибок первого и второго рода Р1 и P2, которые определяются при интегрировании условных распределений отношений правдоподобия (ОП) для гипотез Н1 и Н2. Воспользовавшись соотношениями (3), (5), после громоздких вычислений получим
где
,
- числовые коэффициенты; Г[ ]- гамма-функция; F4 ( ) – гипергеометрическая функция.
Из (6) нетрудно
определить ![]() как
как
где γ
- неполная гамма-функция [5], ![]() 2k
ln(1+
2k
ln(1+![]() ).
).
Соотношение для P2 может быть получено аналогичным образом, если осуществить замену коэффициентов р1→р2 и γ(α,β) →Г(α,β). В частном случае, полагая априорные вероятности классов и цены ошибок равными, вероятность ошибочных решений запишется в виде [6]: рош = 0,5 (Р1+Р2). Несмотря на достаточно громоздкий вид, рош вычисляется с помощью таблиц интегральной функции Х2-распределения. Суммирование при вычислении бесконечного числа членов в (7) можно без ущерба общности заменить конечным числом L, задавшись приемлемой точностью.
Синтез последовательной процедуры обнаружения
В ряде случаев время междупериодной обработки (число периодов k) ограничено. Одним из способов преодоления возникающих при этом сложностей является использование процедуры последовательного распознавания классов "цель - подстилающая поверхность". Критерием качества последовательного правила выбора решения при заданных ошибках является минимум среднего значения размера выборки, необходимой для принятия решения. Оптимальный алгоритм распознавания цели в этом случае сводится к сравнению логарифма ОП с двумя порогами Сi, i=1,2. Соотношения, приведенные выше, являются основой для получения распределения длительности процедуры последовательного распознавания цели с априорно известными параметрами п, р1, р2 при гипотезах Н1, Н2.
После ряда формальных преобразований с использованием табличных интегралов, независимое приближение распределения длительности последовательной процедуры распознавания для гипотез Н1 и Н2 запишется в виде:
где
- переменные пороги, зависящие от параметров условных распределений классов р1, р2, ошибок первого и второго рода и номера периода зондирования.
В соотношении (8) ![]() - интегральная функция распределения логарифма ОП (5),
l,s=1,2.
- интегральная функция распределения логарифма ОП (5),
l,s=1,2.
Приведенное распределение может быть вычислено с использованием таблицы мощности X2 - распределения. Однако, несмотря на принципиальную возможность вычисления по соотношениям (7)-(10), непосредственное их использование приводит к значительным временным затратам. Для практических применений наиболее интересным является случай слабого сигнала.
Вероятность обнаружения в случае слабого сигнала
При этом объем выборки оказывается достаточно большим (k >> 1) и можно полагать, что логарифм ОП (4) в этом случае распределен приближенно по нормальному закону с параметрами
где l=1,2, ![]() - начальные моменты исходного распределения (3),
которые могут быть определены по формулам [5]
- начальные моменты исходного распределения (3),
которые могут быть определены по формулам [5]
Полученные выражения позволяют существенно сократить объем вычислений при расчетах эффективности оптимальных решающих правил. В результате вероятность правильного решения, если верна первая гипотеза, определится как
где ![]() определены через (14),
(15).
определены через (14),
(15).
Аналогично при выполнении второй гипотезы
Вид распределения длительности процедуры распознавания при вышеприведенных предположениях не изменится, если вместо интегрального распределения (11) использовать интегральную функцию нормального распределения с параметрами, определенными соотношениями (14) , (15).
Синтез адаптивной процедуры обнаружения
Найденная эффективность оптимальных процедур
распознавания определяет максимально достижимые границы ошибочных решений.
Если параметры распределения (3) неизвестны, уменьшить неопределенность
возможно их оценкой на этапе обучения. Оценку максимального правдоподобия
параметров ![]() в
замкнутом виде получить не удается. Поэтому воспользуемся оценкой
в
замкнутом виде получить не удается. Поэтому воспользуемся оценкой ![]() , полученной методом
моментов [5]
, полученной методом
моментов [5]
где γ1 - коэффициент асимметрии распределения (3), который может быть найден по физически измеряемым величинам.
Размер обучающих классифицированных выборок при
оценках параметров ![]() может
иметь в общем случае произвольный характер. Очевидно, что ОП (4) с учетом (18)
запишется в виде (5), если известное значение параметра
может
иметь в общем случае произвольный характер. Очевидно, что ОП (4) с учетом (18)
запишется в виде (5), если известное значение параметра ![]() заменить его оценкой. В
соотношении (4) порог L может быть найден следующим образом [7]:
заменить его оценкой. В
соотношении (4) порог L может быть найден следующим образом [7]:
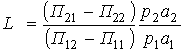 (19)
(19)
где Пl,s l,s=1,2 - коэффициенты потерь, ![]() -априорные
вероятности наблюдения классов 1 и 2; al
может быть определено из соотношения
-априорные
вероятности наблюдения классов 1 и 2; al
может быть определено из соотношения
![]() (20)
(20)
Здесь ![]() - априорное распределение возможных значений
параметра
- априорное распределение возможных значений
параметра ![]() , а
, а
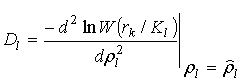 (21)
(21)
Дифференцируя логарифм соотношения (3), после математических преобразований получим:
При указанных выше предположениях относительно
параметров Пl,s, pl, полагая
величины ![]() равномерно распределенными в интервалах
равномерно распределенными в интервалах ![]() для L
можно записать
для L
можно записать
Подставляя (22), (23) в (5), находим решающее правило для адаптивного распознавания классов K1 и K2:
где
.
Устройство, функционирующее в соответствии с
алгоритмом (23), должно определить коэффициент корреляции ОПК по
соотношению (2) для каждого j-го элемента дальности и i-го периода
обзора, произвести вычисления ln![]() и сравнить его с порогом C0, зависящим
от оценок параметров
и сравнить его с порогом C0, зависящим
от оценок параметров ![]() , полученных на этапе обучения по классифицированным
выборкам. Вариант устройства распознавания представлен на рис.1.
, полученных на этапе обучения по классифицированным
выборкам. Вариант устройства распознавания представлен на рис.1.
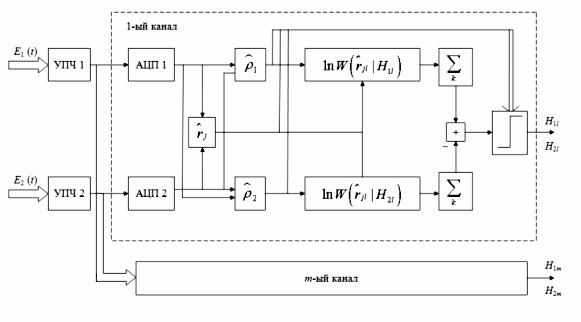
Рис. 1. Структурная схема адаптивного обнаружителя сигнала по корреляции ОПК.
Уместно отметить, что синтезированное устройство может
быть использовано для грубого измерения времени запаздывания ![]() .
После установления факта наличия цели в одном из т каналов,
соответствующих l-му элементу
дальности, оценка
.
После установления факта наличия цели в одном из т каналов,
соответствующих l-му элементу
дальности, оценка ![]() производится
непосредственно по номеру l канала.
производится
непосредственно по номеру l канала.
Эффективность рассмотренного алгоритма в замкнутом виде может быть определена только в предположении большого числа наблюдений с помощью соотношений (9) - (15).
Параметры интегральных функций распределения (16), (17) могут быть найдены непосредственно из (24):
![]() (25)
(25)
![]() (26)
(26)
В (26) ![]() представляет собой дисперсию квадрата
коэффициента корреляции (2), которая может быть найдена при известных
представляет собой дисперсию квадрата
коэффициента корреляции (2), которая может быть найдена при известных ![]() -начальных моментах
распределения
-начальных моментах
распределения ![]() .
С учетом известных соотношений для преобразований распределения вероятностей,
после интегрирования нетрудно найти
.
С учетом известных соотношений для преобразований распределения вероятностей,
после интегрирования нетрудно найти
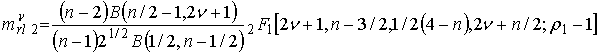 (27)
(27)
Соотношение (26) является основой для расчета ![]() .
.
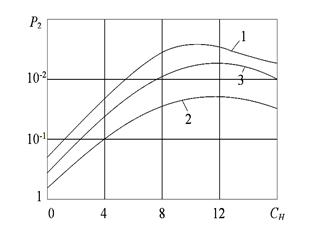
Для сравнения эффективности приведенных алгоритмов
были рассчитаны вероятности ошибочных решений P2 в зависимости от нормированного порога ![]() , а также распределение процедуры последовательного распознавания в случае
полностью известных параметров и при их неопределенности.
, а также распределение процедуры последовательного распознавания в случае
полностью известных параметров и при их неопределенности.
Результаты расчетов приведены на рис. 2,3.
Здесь кривая 1 соответствует сигналу с полностью
известными параметрами, 2 - с параметрами, определенными на этапе
обучения, 3-я кривая отличается от 2 большим значением п (n=100).
Вычисления производились при следующих исходных данных: п=10, k=10, ![]() =0,2,
=0,2, ![]() =0,6. Из рис. 2 видно,
что незнание параметров распределения (3) приводит к проигрышу в
вероятности правильного решения. Увеличение размера выборки, по которой
производится оценка параметров распределения (3), ведет к уменьшению ошибок их
определения, а следовательно, к снижению ошибок распознавания (селекции) цели
на фоне местных предметов.
=0,6. Из рис. 2 видно,
что незнание параметров распределения (3) приводит к проигрышу в
вероятности правильного решения. Увеличение размера выборки, по которой
производится оценка параметров распределения (3), ведет к уменьшению ошибок их
определения, а следовательно, к снижению ошибок распознавания (селекции) цели
на фоне местных предметов.
|
Рис. 2. Зависимость ошибки обнаружения сигнала от нормированного порога. |
Рис. 3. Плотность распределения вероятностей размера решающей статистики. |
Рисунок 3 иллюстрирует достаточно очевидный факт увеличения наиболее вероятного значения размера выборки (кривая 2) в случае априорной неопределенности параметров распределения (3).
Выводы
Таким образом, синтезированы устройства оптимального и адаптивного обнаружения цели на фоне подстилающей поверхности и оценена их эффективность. Результаты расчетов показывают возможность преодоления априорной неопределенности относительно параметров сигналов, отраженных от цели и местных предметов при использовании процедуры обучения. Результаты могут быть использованы при проектировании РЛС, использующих поляриметрическую информацию для обнаружения (селекции) неподвижных целей на фоне подстилающей поверхности.
Литература
1. Акиншин Н.С., Быстров Р.П., Румянцев В.Л., Соколов А.В. Миллиметровая радиолокация: методы обнаружения негауссовских сигналов / под ред. Р.П. Быстрова. //М: Радиотехника, 2010. - 528 с.
2. Джули Д. Поляризационное разнесение в радиолокации. // ТИИЭР. 1986. т. 74. № 2. - с. 6-34.
3. Акимов П.С., Бакут П.А., Богданович В.А.Теория обнаружения сигналов. Под ред. П.А. Бакута. // М.: Радио и связь. 1984. 440 с.
4. Акиншин Р.Н., Ушаков В.А., Лиходеенко К.П. Алгоритм последовательного обнаружения радиолокационных объектов по корреляционным свойствам их поляризационных параметров. // Научный вестник МГТУГА. Серия «Радиоэлектроника» №171(9), 2011. -с.37-40.
5. Крамер Г. Математические методы статистики. Пер. с англ. под ред. А.Н. Колмогорова. // М.: Мир. 1975. - 648 с.
6. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. //М.: ГИФМЛ. 1962. - 1097 с.
7. Репин В.Г., Тартаковский Т.П. Статистический синтез при априорной неопределенности и адаптация информационных систем. //М.: Сов. Радио. 1977. - 432 с.
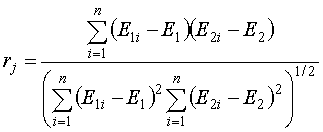
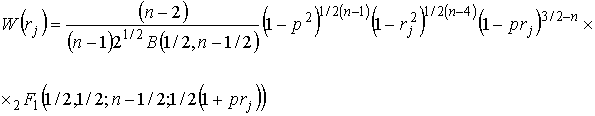 (3)
(3)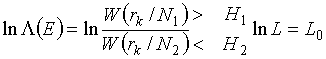
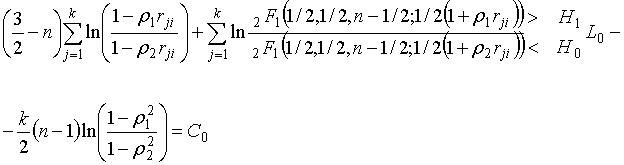 (5)
(5)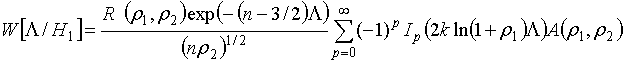 (6)
(6)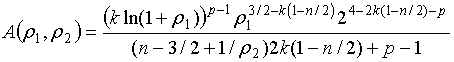

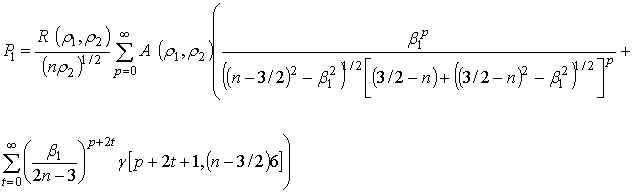
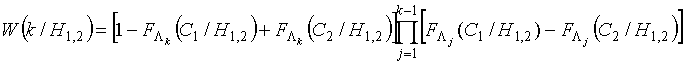 (8)
(8)

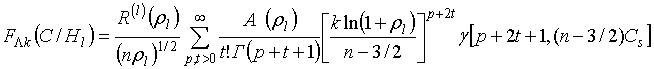 (11)
(11)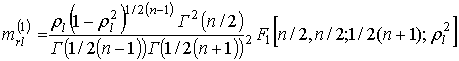
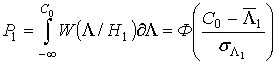
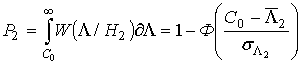
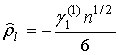
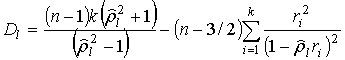
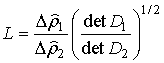
 (24)
(24)