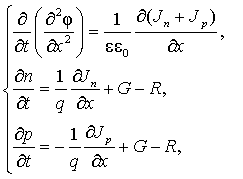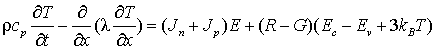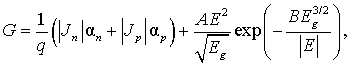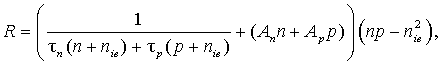УДК 621.382
МОДЕЛИРОВАНИЕ
ФИЗИЧЕСКИХ ПРОЦЕССОВ В
ПОЛУПРОВОДНИКОВЫХ СТРУКТУРАХ
ПРИ ВОЗДЕЙСТВИИ
МОЩНОГО СВЧ-ИМПУЛЬСА. СТРУКТУРЫ С БАРЬЕРОМ ШОТТКИ
С. А. Мещеряков
Федеральное автономное
учреждение "Государственный научно-исследовательский испытательный институт
проблем технической защиты информации ФСТЭК России"
Получена 12 ноября 2013 г.
Аннотация. В рамках численной модели в диффузионно-дрейфовом тепловом приближении приведены результаты моделирования физических процессов, протекающих в кремниевых структурах с барьером Шоттки при воздействии импульсного сверхвысокочастотного электромагнитного излучения. Представлены энергомощностные и температурные характеристики структур в широком диапазоне длительностей однократного импульсного воздействия в зависимости от их конструктивно-технологических параметров.
Ключевые слова: численная модель, диффузия, дрейф, структура с барьером Шоттки, СВЧ-импульс, тепловое поражение.
Abstract. Results of simulation of the physical processes in silicon Schottky-barrier structures at microwave pulse action of electromagnetic radiation are given within the limits of numerical model in drift-diffusion thermodynamic approach. Power and temperature characteristics of structures in durations wide range of the single pulse action depending on their constructive-technological parameters are presented.
Key words: numerical model, diffusion, drift, Schottky-barrier structure, microwave pulse, thermal damage.
Введение
Описанию влияния мощного импульсного сверхвысокочастотного (СВЧ) электромагнитного излучения (ЭМИ) на полупроводниковые структуры посвящен ряд работ. Одной из первых моделей, основанных на экспериментальных исследованиях зависимостей мощности ЭМИ от длительности импульса воздействия и одномерном аналитическом решении однородного уравнения теплопроводности для бесконечного полупроводника, можно считать тепловую модель Вунша-Белла [1]. Она позволяла получить семейство характеристик, из которого в зависимости от предполагаемой температуры выгорания и длительности воздействующего импульса tp с учетом тепловых характеристик полупроводника рассчитывалась мощность выгорания Pburn ~ tp-0.5 и затем для экспериментальных данных выделялась наиболее подходящая.
Дальнейшее развитие модели [1] происходило по пути уточнения решения уравнения теплопроводности исходя из представления локализации тепловой мощности в некоторой точке. В предположении сферического распределения температуры в окрестности этой точки следует отметить работу Таска [2], позволившую описать отличные от модели Вунша-Белла участки "адиабатического" разогрева (Pburn ~ tp-1) в области коротких импульсов ЭМИ (порядка 100 нс) и постоянной мощности (Pburn = const) для длинных импульсов (свыше 100 мкс). Архипов и др. [3] привели аналитическое решение неоднородного уравнения теплопроводности в предположении наличия особой области, локализующей электрическую мощность и связанную с радиационными дефектами. Двайер и др. [4] для импульсов ЭМИ обобщили модели [2, 3] коррекцией предполагаемой температуры выгорания с помощью искусственно вводимого температурного коэффициента, зависящего от длительности импульса и реальной геометрии структуры, разграничив разные участки зависимости Pburn(tp) исходя из времени распространения тепла в различных пространственных направлениях.
Продолжительное время построенная на указанных моделях математическая аппроксимация, известная как модель Вунша–Белла–Таска, давала приемлемое описание экспериментальных данных. Однако последние экспериментальные результаты по воздействию мощных однократных СВЧ-импульсов ЭМИ наносекундного диапазона на электронную аппаратуру показали существенное расхождение с указанной моделью. В частности, в работе [5] экспериментально выявлен рост энергии, необходимой для функционального сбоя полупроводниковых компонентов персонального компьютера, при уменьшении длительности воздействующего импульса, что нельзя объяснить в рамках тепловых моделей [1–4].
В тепловых моделях используются два существенных упрощения. Вся электромагнитная импульсная мощность рассматривается как внешняя и исключительно тепловая, полностью поглощаемая полупроводниковой структурой и приводящая к разогреву и тепловому поражению. При этом предполагается, что тепловая мощность локализована в определенном объеме структуры (как правило, в ее обедненной области), а температура поражения априорно задается (например, как температура контактно-металлизационной системы или плавления полупроводника [1]). Данные упрощения при расчете энергомощностных характеристик теплового поражения позволяют ограничиться рассмотрением только уравнение теплопроводности.
Однако электромагнитный импульс вначале наводит на случайных или штатных антеннах радиоэлектронных устройств электрический сигнал, поступающий на контакты полупроводниковых элементов, а уже затем возникший и протекающий внутри полупроводниковых элементов ток вызывает различные эффекты, в том числе и тепловой разогрев. Иными словами, следует предполагать, что рассеиваемая внутри структуры электрическая энергия может отличаться от внешней энергии воздействующего импульса ЭМИ и расходоваться не только на увеличение объемной температуры, но и на другие термостимулированные физические процессы. В этом случае уравнение теплопроводности обязательно должно рассматриваться как неоднородное с внутренними источниками и приемниками тепла и решаться совместно с уравнениями, описывающими токоперенос в структуре.
Цель настоящей работы – в указанных модельных условиях, отличных от [1–4], дать описание физических процессов в полупроводниковых структурах с барьером Шоттки под воздействием однократного мощного импульсного СВЧ ЭМИ.
Математическая модель
Рассмотрим воздействие импульсного СВЧ ЭМИ на диодную структуру с барьером Шоттки. Будем исходить из предположения, что в зависимости от уровня мощности внешнего импульса ЭМИ на структуру воздействует наведенный электрический сигнал u(t) с некоторой амплитудой напряжения U0, пропорциональной мощности импульсного ЭМИ, и несущей частотой f. Результатом воздействия является электрический ток i(t), протекающий внутри диода и поступающий далее в тракт обработки сигнала. По мере увеличения уровня мощности увеличивается и амплитуда напряжения, в результате чего состояние диодной структуры может переходить из рабочего режима в область функциональных сбоев, а затем и в область теплового поражения (выгорания). При данном допущении можно использовать общий подход в описании указанных режимов, отличающихся лишь характеристиками внешнего воздействия. Будем также предполагать, что волноводная секция, содержащая диод, настроена на прием СВЧ-сигнала соответствующей частоты, обеспечивая максимально возможное поглощение энергии ЭМИ, и полученные модельные расчеты соответствуют наиболее эффективному энергетическому воздействию на исследуемую структуру.
Для моделирования физических процессов в диодной структуре воспользуемся известной системой одномерных дифференциальных уравнений в частных производных в рамках диффузионно-дрейфового теплового приближения (ДДМТ) [6]. Данная система включает уравнение полного тока и два уравнения непрерывности для электронов и дырок, дополненные уравнениями переноса тока и уравнением теплопроводности:
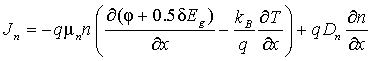 , (2)
, (2)
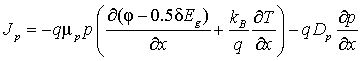 , (3)
, (3)
где φ – электрический потенциал, q – заряд электрона, e0 – диэлектрическая постоянная, e – диэлектрическая проницаемость полупроводника; n, p – концентрация электронов и дырок; Jn, Jp – плотности тока электронов и дырок; G, R – суммарный темп генерации и рекомбинации; mn, mp – подвижности электронов и дырок; dEg – сужение ширины запрещенной зоны в зависимости от степени легирования, kB – постоянная Больцмана, T – температура; Dn, Dp – коэффициенты диффузии электронов и дырок; r – плотность вещества, cp – удельная теплоемкость вещества, l – коэффициент теплопроводности полупроводника, E – напряженность электрического поля; Ec, Ev – энергетические уровни дна зоны проводимости и потолка валентной зоны.
Темп генерации G, входящий в систему (1) и уравнение (4) с учетом процессов ударной ионизации и туннелирования может быть представлен как
где αn, αp – коэффициенты ударной ионизации электронов и дырок; A, B – коэффициенты туннельной генерации; Eg – ширина запрещенной зоны полупроводника.
Общий темп рекомбинации, включающий рекомбинацию Шокли-Рида-Холла и Оже-рекомбинацию, представляется уравнением
где τn, τp – времена жизни электронов и дырок; nie – собственная концентрация примеси в полупроводнике с учетом эффектов сильного легирования и сужения запрещенной зоны; An, Ap – коэффициенты Оже-рекомбинации электронов и дырок.
Согласно уравнению (4) рассеиваемая внутри диодной структуры электрическая мощность преобразуется в Джоулево тепло и термостимулированные генерационно-рекомбинационные процессы. Это приводит к изменению объемной температуры, и следовательно, через изменение электрофизических параметров материала к изменению электрического режима, а через измененную электрическую рассеиваемую мощность к новому изменению температуры (тепловая обратная связь). Заметим также, что рекомбинационные процессы происходят с выделением тепла, а генерационные – с его поглощением.
Уравнения (1) – (4) являются нелинейными, и в общем случае разрешимы только численными методами. Для решения уравнений задаются следующие граничные и начальные условия. Потенциал на контакте Шоттки диодной структуры в момент времени t определяется приложенным напряжением u(t), омический контакт заземлен (u = 0). Концентрации свободных носителей заряда на теплоотводящем (температура структуры равна температуре окружающей среды) омическом контакте берутся равными равновесным концентрациям, на теплоизолированном (градиент температуры нулевой) контакте Шоттки – согласно теории Кроуэлла–Зи [7]. Начальным условием являются внутренние распределения поля и концентраций свободных носителей заряда в диоде при соответствующем режиму эксплуатации постоянном смещении.
Результаты моделирования
Модельные вычисления будем производить для полупроводниковых структур с барьером Шоттки на основе кремния, соответствующих параметрам промышленно выпускаемых детекторных и смесительных диодов, используемых в приемных трактах радиоэлектронной аппаратуры. Электрофизические параметры кремния (подвижности и времена жизни свободных носителей заряда, теплопроводность и др.) и их зависимости от температуры взяты в соответствии с [8].
На рис. 1 представлен профиль распределения легирующей примеси N(x) в кремниевой диодной структуре с барьером Шоттки. Он состоит из трех областей: низколегированной эпитаксиальной пленки толщиной wn = 3 мкм и уровнем легирования Nd = 1015 см-3, высоколегированной монокристаллической подложки толщиной wn+ = 200 мкм и уровнем легирования Nd+ = 5´1018 см-3 и области приконтактного легирования толщиной wn++ = 2 мкм и уровнем легирования Nd++ = 5´1019 см-3. К эпитаксиальной пленке примыкает теплоизолированный выпрямляющий контакт Шоттки с высотой потенциального барьера Fb = 0.7 эВ, с другой стороны структуры – омический теплоотводящий контакт. В дальнейшем будем использовать указанные параметры по умолчанию, если иное не оговорено отдельно. Там же представлены статические вольт-амперные характеристики для данной структуры в прямом и обратном смещении, полученные расчетным путем на основе уравнений (1) – (4) при равенстве нулю временных производных и замене уравнения полного тока на уравнение Пуассона.
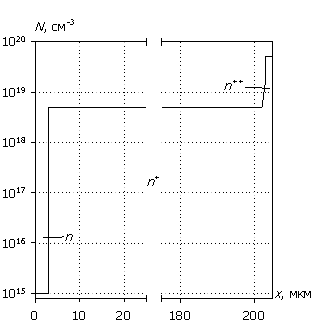
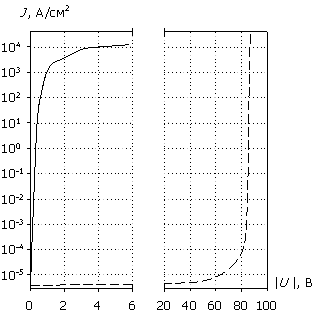
Рис. 1. Профиль
легирующей примеси и вольт-амперные характеристики (сплошная линия – прямая
характеристика, штриховая линия – обратная
характеристика).
Рассмотрим поведение данной структуры при нулевом постоянном смещении и воздействии на нее СВЧ-импульса с несущей частотой f = 1 ГГц. На рис. 2 приведены зависимости рассеиваемых в структуре плотности энергии и средней плотности мощности в зависимости от длительности импульсного СВЧ-воздействия с заданной амплитудой напряжения U0, определяемые следующим образом. Интегрирование по длине моделируемой структуры правой части уравнения (4) дает мгновенную рассеиваемую плотность мощности P(t). Плотность энергии W, рассеиваемая за время импульса tp, и средняя плотность мощности за время импульса Pmean вычисляются из выражений:
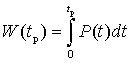 , (7)
, (7)
![]() . (8)
. (8)
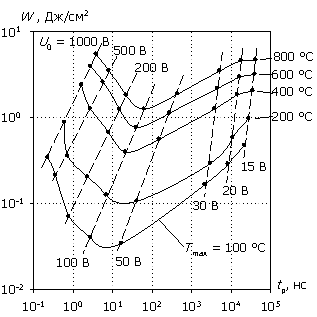
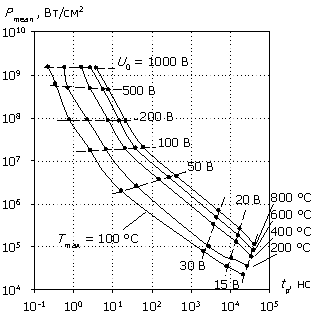
Рис. 2. Зависимости
W(tp) и Pmean(tp) (в
качестве параметров – значения
амплитуды напряжения U0 воздействующего
сигнала и максимальная
температура внутри структуры Tmax).
Из рис. 2 видно, что характеристика W(tp) для исследуемой структуры имеет область минимума энергии, приходящуюся в зависимости от температуры теплового разогрева на диапазон длительности импульса 5...70 нс. Интерес вызывает участок левее области минимума, где с уменьшением длительности воздействия наблюдается рост энергии, необходимой для разогрева до определенной температуры. Этот участок не может быть описан в рамках известных тепловых моделей [1–4], но, как будет показано ниже, имеет удовлетворительное описание в рамках ДДМТ, основанное на представлении генерационных процессов как приемника тепловой энергии.
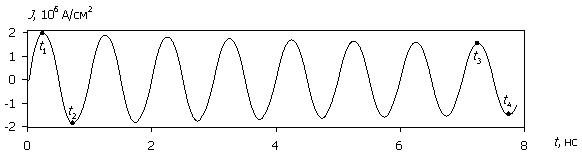
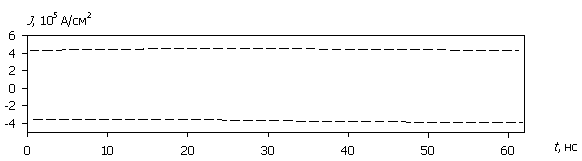
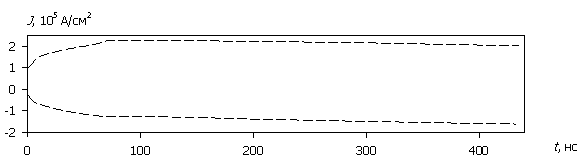
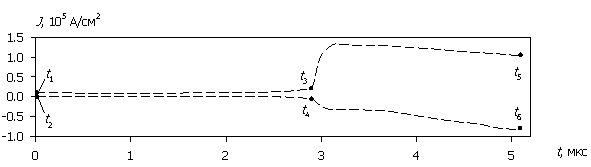
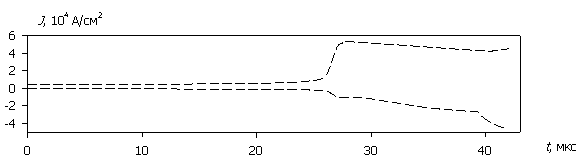
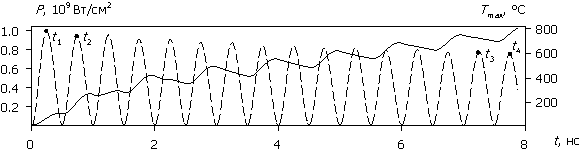
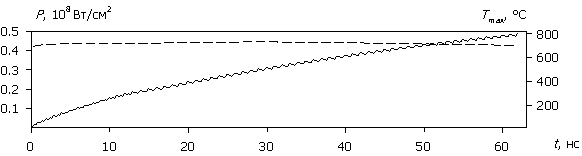
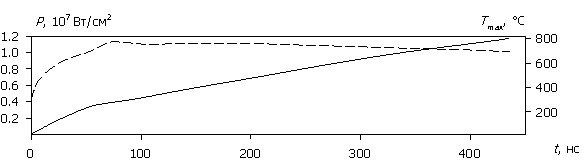
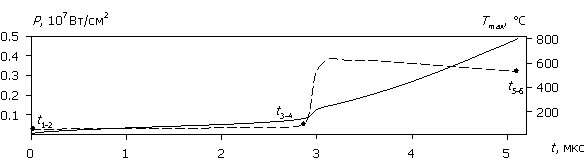
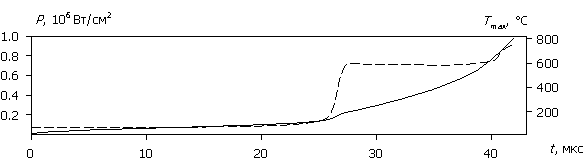
Рассмотрим внутренние процессы, протекающие в полупроводниковой структуре и приводящие к зависимостям на рис. 2. На рис. 3а – 3д приведены временные диаграммы плотности тока J(t), протекающего через структуру, рассчитанные для различных значений амплитуды напряжения воздействующего сигнала (для больших временных интервалов пунктиром показаны огибающие). На рис. 4а – 4д приведены временные диаграммы рассеиваемой мгновенной плотности мощности P(t) и соответствующей максимальной температуры Tmax(t) в моделируемой структуре. Расчет проводился до значения максимальной температуры 800 ºC.
Сопоставление зависимостей на рис. 3, 4 показывает, что при относительно малых значениях амплитуды напряжения воздействующего сигнала (15...30 В) существует достаточно протяженный начальный участок, где диодная структура сохраняет выпрямляющие свойства, рассеиваемая мощность относительно невысока, а температура разогрева не превышает 100...150 ºC. При дальнейшем увеличении времени воздействия начинает наблюдаться рост как прямого, так и обратного тока с ухудшением выпрямляющих свойств структуры. Температура теплового разогрева в этом временном диапазоне не превышает 200...250 ºC. Далее структура окончательно теряет выпрямляющие свойства, и обратный ток практически сравнивается с прямым.
(а)
(б)
(в)
(г)
(д)
Рис. 3. Зависимость J(t); (а) – (д) соответствуют U0 = 500, 100, 50, 30, 15 В.
(а)
(б)
(в)
(г)
(д)
Рис. 4. Зависимости P(t) (штриховые
линии) и Tmax(t) (сплошные
линии);
(а) – (д) соответствуют U0 = 500, 100, 50,
30, 15 В.
При увеличении амплитуды воздействующего сигнала (U0 > 30 В) начальный участок быстро сокращается и уже при U0 = 50 В исчезает. При этом структура изначально пропускает ток в обоих направлениях практически одинаково, а рассеиваемая мгновенная мощность P стабилизируется во всем временном интервале.
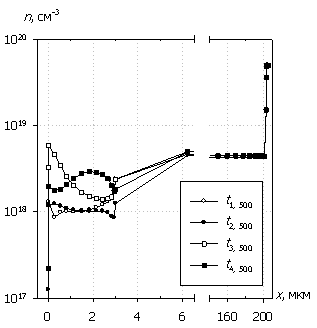
На рис. 5, 6 приведены пространственные распределения внутренних характеристик, соответствующие отмеченным временным точкам на рис. 3а, 4а. Из представленных рисунков видно, что диодная структура при амплитуде входного сигнала U0 = 500 В переходит в режим существенной модуляции проводимости, как в прямом, так и в обратном смещении. Наличие двух изотипных переходов – n – n+ и n+– n++ приводят, аналогично поведению статических характеристик структуры [9,10], к накоплению свободных носителей заряда, особенно в низколегированной области, и превышению их концентраций на несколько порядков относительно равновесных значений.
Это состояние поддерживается при прямой полуволне воздействующего сигнала инжекцией носителей из высоколегированной подложки, а при обратной полуволне – превышающей экстракцию ударной ионизацией, связанной со значительной напряженностью электрического поля, и вызывающей, согласно уравнению (5), процесс лавинного умножения носителей заряда в областях барьера и изотипных переходов. При этом темп генерации растет как за счет увеличения токов проводимости, так и за счет существенных значений коэффициентов ударной ионизации. Ситуация усугубляется снижением подвижности свободных носителей заряда и уменьшением теплопроводности в наиболее подверженных разогреву областях структуры. В результате этого максимальная рассеиваемая мощность локализуется у теплоизолированного контакта с барьером Шоттки и там же происходит наибольший рост температуры. Следует также заметить, что в этой области (порядка 0.5 мкм) темп генерации превышает темп рекомбинации и, согласно уравнению (4), в ней будет затрачиваться часть мощности на генерацию носителей, тем самым несколько замедляя рост температуры. С течением времени рост температуры и распространение тепла вглубь полупроводниковой структуры, а также экранирование накопленными свободными носителями заряда электрического поля, снижают дрейфовые компоненты токов проводимости Jn и Jp, что приводит к общему снижению тока.
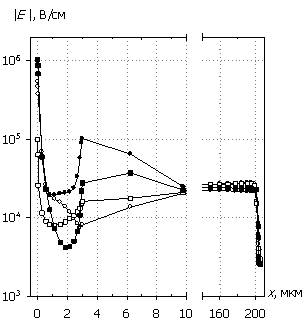
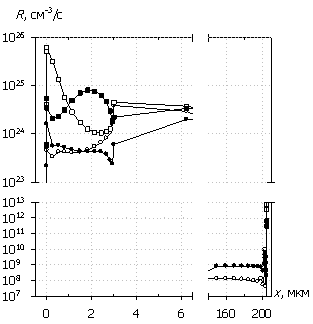
Рис. 5. Распределения
электронов n(x), дырок p(x),
электрического поля E(x) и темпа рекомбинации
R(x); U0 = 500 В.
Маркеры
кривых соответствуют n(x).
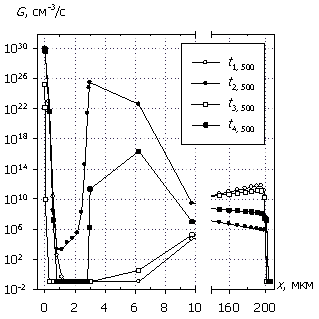
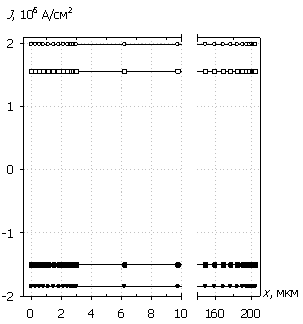
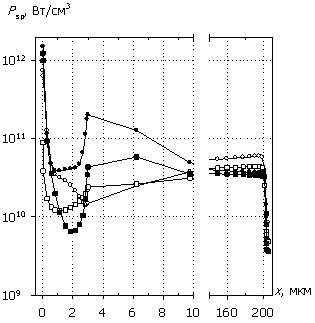
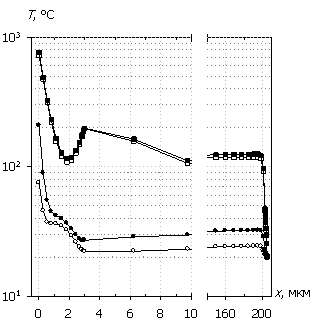
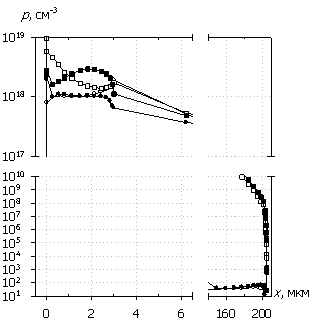
Рис. 6. Распределения
темпа генерации G(x), плотности
тока J(x), рассеиваемой удельной
электрической мощности Psp(x)
и температуры T(x); U0 = 500 В.
Маркеры кривых соответствуют G(x).
Несколько иная картина наблюдается при относительно малых амплитудах воздействующих сигналов. На рис. 7, 8 приведены пространственные распределения внутренних характеристик, соответствующие отмеченным временным точкам на рис. 3г, 4г. В этом режиме напряженности электрического поля изначально недостаточно для ударной ионизации, способной обеспечить режим лавинной генерации носителей. В результате этого возникает участок постепенной "накачки" носителей заряда за счет процессов инжекции на прямой полуволне сигнала в низколегированную область и медленный рост температуры.
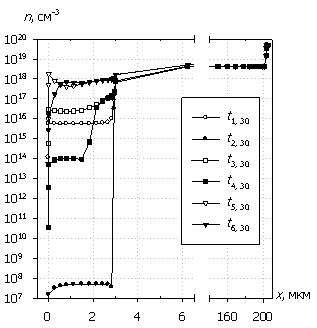
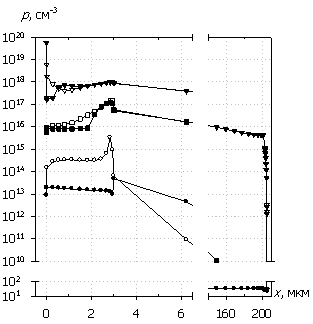
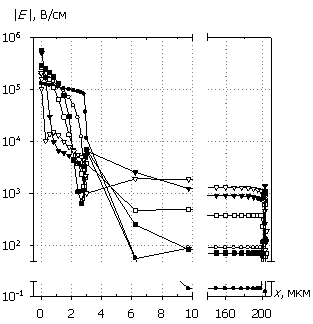
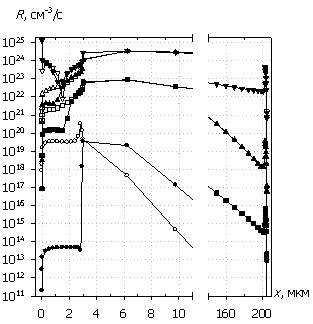
Рис. 7. Распределения электронов
n(x), дырок p(x),
электрического поля E(x) и темпа рекомбинации
R(x); U0 = 30 В.
Маркеры
кривых соответствуют n(x).
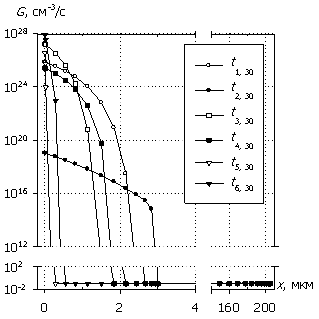
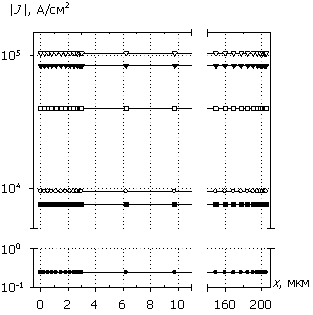
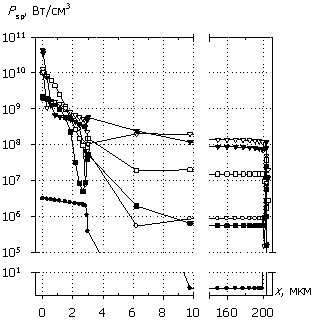
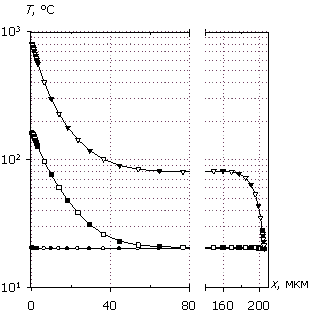
Рис. 8. Распределения
темпа генерации G(x), плотности
тока J(x), рассеиваемой
удельной электрической мощности Psp(x)
и температуры T(x); U0 = 30 В.
Маркеры кривых соответствуют G(x).
Как только проводимость структуры возрастает и обратный ток достигает некоторого значения, начинается развитие генерационных процессов, амплитуда колебаний тока начинает возрастать, что проводит к более крутому росту рассеиваемой мощности и температуры. В отличие от больших уровней сигнала в данном случае темп генерации растет, в основном, за счет увеличения токов проводимости. При этом распространение температурного поля вглубь структуры за счет механизма теплопроводности происходит на значительное расстояние вплоть до теплоотводящего омического контакта. Параллельно с этим происходит экранирование электрического поля вблизи барьерного контакта и уменьшение области, подверженной лавинной генерации.
Приведенные результаты показывают сложность взаимодействия электрического и теплового поля во времени, характеризующую тепловую обратную связь. Перераспределение мощности между компонентами уравнения (4) с учетом зависимостей электрофизических параметров, как от поля, так и от температуры позволяет предположить, что конструкционные параметры структуры и характеристики воздействующего сигнала должны влиять на вид зависимостей W(tp).
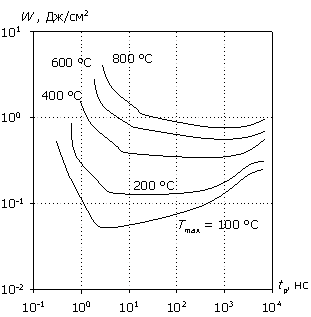
На рис. 9 представлена характеристика W(tp) при разной толщине эпитаксиальной пленки. Как уже отмечалось, рассеиваемая мощность локализуется в области низколегированной пленки, формируя при относительно коротких временах воздействия "адиабатический" участок. Увеличение толщины пленки растягивает во времени процесс накопления тепла. Одновременно с этим несколько уменьшается напряженность электрического поля, снижая темп генерации. Действие этих механизмов приводит к расширению адиабатического участка. Аналогичного результата можно достичь увеличением несущей частоты СВЧ-импульса при фиксированном значении толщины эпитаксиальной пленки.
Расчеты показывают, что характеристика W(tp) практически не зависят от степени легирования эпитаксиальной пленки структуры. Как видно из распределений на рис. 5 – 8 концентрации свободных носителей в эпитаксиальной пленке стремятся к уровню легирования подложки, а следовательно, уровень легирования эпитаксиальной пленки в данных "жестких" режимах не может оказать существенного влияния.
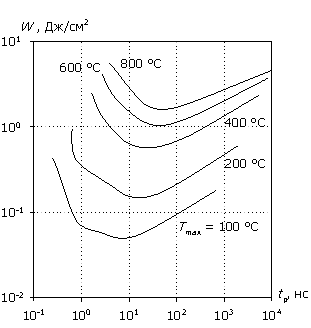
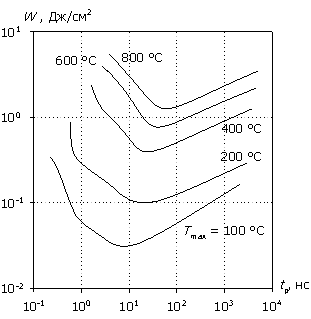
(а) (б)
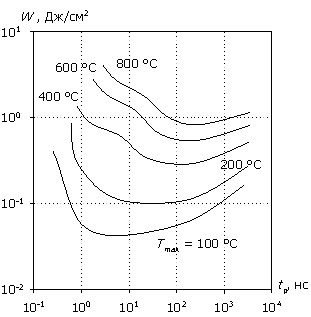
(в) (г)
Рис. 9. Зависимость W(tp) для различных значений толщины эпитаксиальной пленки; (а) – (г) соответствуют wn = 1, 3, 6, 10 мкм.
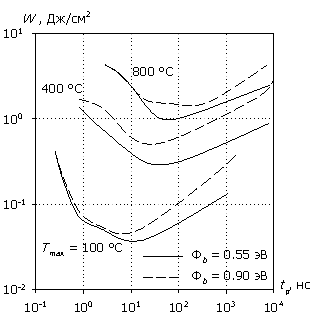
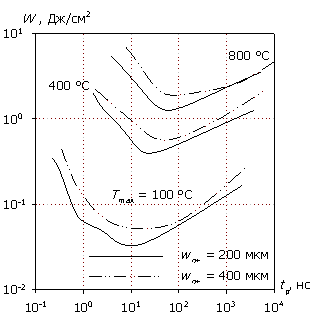
На рис. 10 представлена характеристика W(tp) в зависимости от высоты барьера Шоттки и от толщины высоколегированной подложки для характерных кремниевой технологии диапазонов значений. С увеличением высоты барьера Шоттки рассеиваемая энергия, необходимая для разогрева структуры до определенной температуры, увеличивается. Причиной этому является рост напряженности электрического поля в области барьерного контакта при увеличении значения Fb и усиление генерационных процессов, что приводит к снижению мощности, идущей непосредственно на тепловой разогрев согласно уравнению (4). С увеличением толщины подложки от 200 до 400 мкм рассеиваемая энергия также несколько увеличивается за счет процессов распространения и накопления тепла в большем объеме.
(а) (б)
Рис. 10. Зависимость W(tp) для различных
значений высоты барьера Шоттки
Fb (а) и толщины
подложки wn+ (б).
Заключение
Моделирование в рамках ДДМТ полупроводниковой структуры с барьером Шоттки позволяет описать как известные в настоящее время характерные участки поведения энергомощностных характеристик полупроводниковых структур, так и участок роста энергии в области сверхкоротких импульсов. Результаты моделирования показывают, что характеристики W(tp) имеют выраженный минимум энергии, лежащий в диапазоне 5...100 нс в зависимости от конструктивно-технологических параметров структуры. Выявленный в [5] рост энергии теплового поражения в области сверхкоротких СВЧ-импульсов связан с развитием генерационных процессов, поглощающих часть рассеиваемой внутри структуры мощности.
Из основных конструктивно-технологических параметров структуры с барьером Шоттки наибольшее влияние на ее энергетические характеристики теплового разогрева СВЧ-импульсом имеет толщина эпитаксиальной пленки. Как следует из представленных результатов моделирования, увеличение толщины пленки в 10 раз в рамках типовых значений приводит к расширению области адиабатического разогрева приблизительно на 2 порядка. Менее значимыми параметрами являются высота барьера Шоттки и толщина высоколегированной подложки, где разница в оценке энергии, требуемой для достижения определенной температуры разогрева, не превышает 2 раз.
Рассчитанные в рамках ДДМТ зависимости W(tp) и Pmean(tp) позволяют выделить три области: область рабочего режима, соответствующую рабочим температурам полупроводникового диода (Tmax < 120...150 ºС), область функциональных сбоев (120...150 ºС < Tmax < 300...400 ºС), не приводящую к катастрофическим разрушением полупроводниковой структуры, и область теплового поражения (Tmax > 300...400 ºС), связанную с разрушением, в первую очередь, контактно-металлизационной системы в области теплоизолированного барьера Шоттки.
Литература
1. D.C. Wunsh, R.R. Bell. Determination of threshold failure levels of semiconductor diodes and transistors due to pulse voltage // IEEE Trans. 1968. V. NS-15. P. 244–259.
2. D.M. Taska. Pulse power failure modes in semiconductors // IEEE Trans. 1970. V. NS-17. P. 364.
3. V.I. Arkhipov, E.R. Astvatsaturyan, V.A. Godovitsyn, A.I. Rudenko. Stationary and non-stationary spatial temperature distributions in semiconductors, caused by pulse voltage // Int. J. Electronics. 1983. V. 55. P. 395.
4. V.M. Dwyer, A.J. Franklin, D.S. Campbell. Thermal failure in semiconductor devices // Solid-State Electron. 1990. V.33. P. 553–560.
5. Ю.Г. Юшков, П.Ю. Чумерин, С.Н. Артеменко и др. Экспериментальное исследование воздействия сверхвысокочастотных импульсов на работу персонального компьютера // Радиотехника и электроника. 2001. Т. 46. №8. С. 1020–1024.
6. G.K. Wachutka. Rigorous thermodynamic treatment of heat generation and conduction in semiconductor device modeling// IEEE Trans. 1990. V. CAD-9. P. 1141–1149.
7. S.M. Sze, K.Ng. Kwok. Physics of Semiconductor Devices. Hoboken, New Jersey: Wiley-Interscience, 2007.
8. NSM Archive – Physical Properties of Semiconductors // [Электронный ресурс]. URL: http://www.ioffe.rssi.ru\SVA\NSM\Semicond\index.html
9. С.А. Мещеряков, А.И. Прокопьев. Влияние барьерных свойств низкоомной подложки на модуляцию сопротивления базы диода Шоттки // Изв. вузов. Электроника. 1998. № 2. С. 27–29.
10. A.I. Prokopyev, S.A. Mesheryakov. Static characteristics of high-barrier Schottky diode under high level injection // Solid-St. Electron. 1999. V 43. N 9. P. 1747–1753.