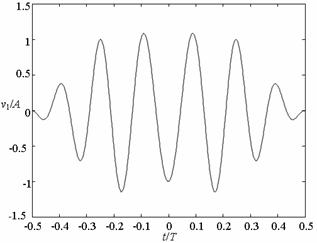
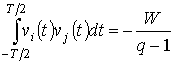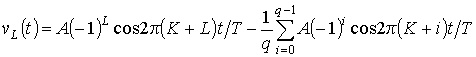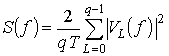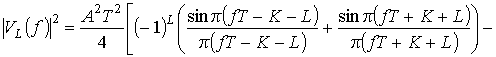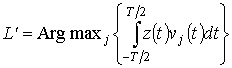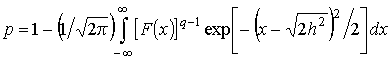УДК 621.391
ПЕРЕДАЧА ДВОИЧНЫХ СООБЩЕНИЙ
СИМПЛЕКСНЫМИ СИГНАЛАМИ
В. А. Вершинин
Рыбинский
государственный авиационный технический университет им. П. А. Соловьева
Статья
получена 13 сентября 2013 г., после доработки – 25 ноября 2013 г.
Аннотация. В работе рассматривается передача двоичных сообщений с использованием симплексных элементарных сигналов. Определена полоса частот, занимаемая сигналом на основе различных элементарных сигналов. Произведена оценка помехоустойчивости передачи. Исследована эффективность использования симплексных элементарных сигналов.
Ключевые слова: симплексные сигналы, полоса частот, помехоустойчивость.
Abstract: The paper considers the transmission of binary messages using simplex elementary signals. Defined frequency band occupied by a signal on the basis of different elementary signals. An assessment is made of immunity of the transfer. The efficiency of use of simplex elementary signals.
Key words: simplex signals, bandwidth, immunity to interference.
1. Введение
Под двоичным сообщением будем понимать
последовательность элементов, каждый из которых имеет длительность ![]() и может принимать с равной вероятностью два
значения. Перед передачей двоичное сообщение может делиться на блоки, каждый из
которых состоит из k элементов. Таким образом, блок элементов двоичного
сообщения имеет длительность
и может принимать с равной вероятностью два
значения. Перед передачей двоичное сообщение может делиться на блоки, каждый из
которых состоит из k элементов. Таким образом, блок элементов двоичного
сообщения имеет длительность ![]() и может принимать
и может принимать ![]() значений, вероятность каждого значения
значений, вероятность каждого значения ![]() . При отсутствии деления на блоки
. При отсутствии деления на блоки ![]() ,
, ![]() ,
, ![]() . Каждому значению блока на выходе модулятора
соответствует один из q элементарных сигналов. Сигнал на выходе модулятора
можно представить в виде:
. Каждому значению блока на выходе модулятора
соответствует один из q элементарных сигналов. Сигнал на выходе модулятора
можно представить в виде:
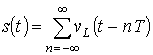 ,
(1)
,
(1)
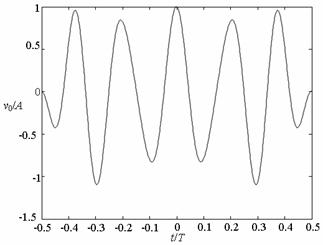
где ![]() – сигнал,
соответствующий n-му блоку сообщения; t – время; L –
номер элементарного сигнала (
– сигнал,
соответствующий n-му блоку сообщения; t – время; L –
номер элементарного сигнала (![]() ). Таким образом,
). Таким образом, ![]() является одним из следующих элементарных
сигналов:
является одним из следующих элементарных
сигналов: ![]() ,
, ![]() , …,
, …, ![]() . Длительность элементарного сигнала –
величина временного интервала, за пределами которого отсутствуют ненулевые
значения сигнала. Будем считать, что таким интервалом для сигнала
. Длительность элементарного сигнала –
величина временного интервала, за пределами которого отсутствуют ненулевые
значения сигнала. Будем считать, что таким интервалом для сигнала ![]() является интервал от
является интервал от ![]() до
до ![]() , и в
дальнейшем элементарные сигналы будут задаваться только на этом интервале. Элементарные
сигналы могут представлять собой прямоугольные импульсы или импульсы другой
формы. От этого зависит полоса частот, занимаемая сигналом
, и в
дальнейшем элементарные сигналы будут задаваться только на этом интервале. Элементарные
сигналы могут представлять собой прямоугольные импульсы или импульсы другой
формы. От этого зависит полоса частот, занимаемая сигналом ![]() .
.
В качестве элементарных сигналов широко используются ортогональные сигналы [1]. Для этих сигналов
 при
при ![]() , и
, и 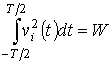 ,
,
где ![]() ;
; ![]() ; W – энергия элементарного сигнала. Часто используются
гармонические ортогональные сигналы следующего вида:
; W – энергия элементарного сигнала. Часто используются
гармонические ортогональные сигналы следующего вида:
где A – амплитуда сигнала; K – целое положительное число, определяющее положение
полосы частот, занимаемой сигналом ![]() . Множитель
. Множитель ![]() вводится для исключения скачков
значений при переходе от одного элементарного сигнала к другому. Это приводит к
уменьшению полосы частот, занимаемой сигналом
вводится для исключения скачков
значений при переходе от одного элементарного сигнала к другому. Это приводит к
уменьшению полосы частот, занимаемой сигналом ![]() . Энергия этих элементарных сигналов
. Энергия этих элементарных сигналов ![]() .
.
В качестве элементарных сигналов можно использовать сигналы [2], для которых выполняются следующие условия:
где W – энергия элементарного
сигнала. При ![]() эти сигналы являются противоположными.
Обычно q таких
сигналов формируются на основе
эти сигналы являются противоположными.
Обычно q таких
сигналов формируются на основе ![]() ортогональных функций:
ортогональных функций:
![]() ,
, ![]() , …,
, …, ![]() , при этом дается следующая геометрическая
интерпретация. В пространстве размерностью
, при этом дается следующая геометрическая
интерпретация. В пространстве размерностью ![]() элементарные
сигналы представляются q точками,
которые являются вершинами симплекса. Поэтому сигналы, удовлетворяющие условиям
(3) принято называть симплексными. Если использовать гармонические ортогональные
функции вида:
элементарные
сигналы представляются q точками,
которые являются вершинами симплекса. Поэтому сигналы, удовлетворяющие условиям
(3) принято называть симплексными. Если использовать гармонические ортогональные
функции вида: ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , ...,
, ...,
то для ![]() получаем следующие симплексные
(противоположные) сигналы:
получаем следующие симплексные
(противоположные) сигналы:
Для ![]() нетрудно получить симплексные
сигналы:
нетрудно получить симплексные
сигналы:
![]() ,
,
![]() ,
,
![]() .
(5)
.
(5)
Элементарные
сигналы этого вида обладают следующим недостатком. При переходе от одного
элементарного сигнала к другому может возникать скачок значения, что расширяет
полосу частот, занимаемую сигналом ![]() .
.
Симплекс с q вершинами
может существовать и в пространстве размерностью большей ![]() . В [3] предложено формировать q элементарных
симплексных сигналов, удовлетворяющих (3), на основе q ортогональных
функций
. В [3] предложено формировать q элементарных
симплексных сигналов, удовлетворяющих (3), на основе q ортогональных
функций ![]() ,
, ![]() , …,
, …, ![]() следующим образом:
следующим образом:
Нетрудно показать, что энергия такого элементарного
сигнала ![]() , где
, где 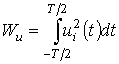 .
Если в качестве ортогональных функций использовать гармонические функции вида
(2), т.е.
.
Если в качестве ортогональных функций использовать гармонические функции вида
(2), т.е. ![]() , то из (6)
, то из (6)
Энергия
этих элементарных сигналов ![]() .
.
При ![]() на основании (7)
на основании (7)
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
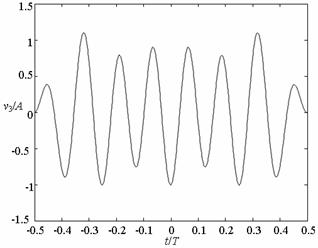
На рис. 1а
, 1б, 1в и 1г показаны временные зависимости для симплексных элементарных
сигналов ![]() ,
, ![]() ,
, ![]() и
и ![]() соответственно при
соответственно при ![]() . К достоинствам этих сигналов следует
отнести отсутствие скачков значений при переходе от одного элементарного
сигнала к другому.
. К достоинствам этих сигналов следует
отнести отсутствие скачков значений при переходе от одного элементарного
сигнала к другому.
|
а |
б |
|
в |
г |
|
Рис. 1. Симплексные элементарные сигналы (7) при |
|
Целью данной работы является исследование эффективности использования симплексных элементарных сигналов (7).
2. Полоса частот, занимаемая сигналом
Сигнал ![]() , определяемый согласно
(1), в общем случае является случайным сигналом. Будем считать значения
блоков элементов двоичного сообщения независимыми случайными величинами. Полоса
частот, занимаемая сигналом, может определяться различными методами. Определим
полосу частот F, занимаемую сигналом, исходя из
спектральной плотности мощности этого сигнала
, определяемый согласно
(1), в общем случае является случайным сигналом. Будем считать значения
блоков элементов двоичного сообщения независимыми случайными величинами. Полоса
частот, занимаемая сигналом, может определяться различными методами. Определим
полосу частот F, занимаемую сигналом, исходя из
спектральной плотности мощности этого сигнала ![]() , где f – частота. При этом будем
считать, что в полосе частот F должно быть сосредоточено
99% мощности сигнала
, где f – частота. При этом будем
считать, что в полосе частот F должно быть сосредоточено
99% мощности сигнала 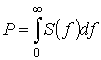 . Тогда
. Тогда
где ![]() и
и ![]() –
нижняя и верхняя граничные частоты определяются из выражений:
–
нижняя и верхняя граничные частоты определяются из выражений: 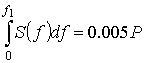 ;
;  .
.
Спектральная
плотность мощности может быть определена для стационарных (в широком смысле)
случайных сигналов с нулевым математическим ожиданием. Если математическое ожидание
![]() , равное
, равное
то и
математическое ожидание сигнала ![]() будет нулевым. Для рассмотренных
выше симплексных сигналов (4), (5) и (7) условие (9) выполняется. При этом [3]
будет нулевым. Для рассмотренных
выше симплексных сигналов (4), (5) и (7) условие (9) выполняется. При этом [3]
где  – спектральная плотность сигнала
– спектральная плотность сигнала ![]() .
.
Для элементарных сигналов (4) на основании (10)
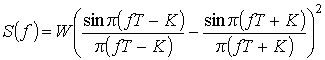 ,
(11)
,
(11)
где  – энергия элементарного сигнала.
– энергия элементарного сигнала.
Для элементарных сигналов (5), исходя из (10),
 ,
,

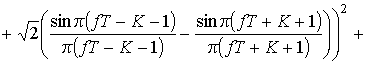
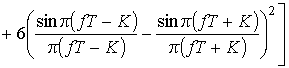 ,
,

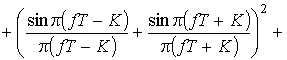
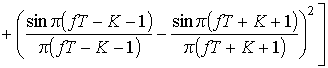 , (12)
, (12)
где  – энергия элементарного сигнала.
– энергия элементарного сигнала.
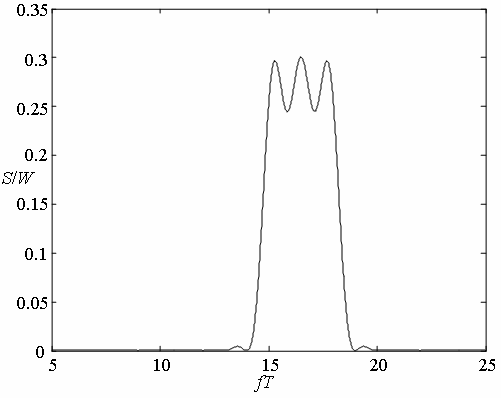
На рис.
2 показана зависимость ![]() от
от
![]() для
для ![]() при использовании элементарных сигналов (4),
полученная на основании (11), а на рис. 3 – та же зависимость для элементарных
сигналов (5), полученная с помощью (12).
при использовании элементарных сигналов (4),
полученная на основании (11), а на рис. 3 – та же зависимость для элементарных
сигналов (5), полученная с помощью (12).
|
|
|
Рис. 2. Спектральная плотность мощности для сигналов (4) |
|
|
|
Рис. 3. Спектральная плотность мощности для сигналов (5) |
Для элементарных сигналов (7)
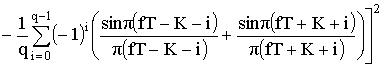 ,
,
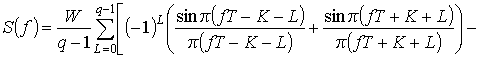
 , (13)
, (13)
где  – энергия элементарного сигнала.
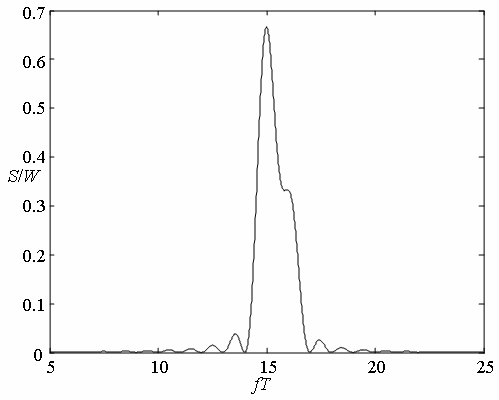
На рис. 4 и 5 показаны зависимости
– энергия элементарного сигнала.
На рис. 4 и 5 показаны зависимости ![]() от
от
![]() , полученные с
использованием (13) для
, полученные с
использованием (13) для ![]() , при
, при ![]() и
и ![]() соответственно.
соответственно.
|
|
|
Рис. 4. Спектральная плотность мощности для сигналов
(7) при |
|
|
|
Рис. 5. Спектральная плотность мощности для сигналов
(7) при |
Для ![]() на основании (11), (12) и (8) можно
получить значение занимаемой полосы частот F при использовании элементарных сигналов (4) и (5) соответственно
на основании (11), (12) и (8) можно
получить значение занимаемой полосы частот F при использовании элементарных сигналов (4) и (5) соответственно
![]() и
и ![]() .
.
При
использовании элементарных сигналов (7) и ![]() на основании (13) и (8) для
значений q равных 2, 4 и 8 получено значение
занимаемой полосы частот F соответственно
на основании (13) и (8) для
значений q равных 2, 4 и 8 получено значение
занимаемой полосы частот F соответственно ![]() ,
, ![]() и
и ![]() .
.
Ортогональные сигналы вида (2) свойством (9) не обладают. В этом случае для оценки полосы частот, занимаемой сигналом, необходимо применять другие методы. В [3] для сигналов этого вида получены значения занимаемой полосы частот практически совпадающие со значениями, полученными выше для сигналов (7).
Таким
образом, сигнал ![]() на
основе элементарных сигналов вида (4) и (5) занимает в несколько раз более широкую
полосу частот, чем сигнал на основе симплексных элементарных сигналов (7) или
сигнал на основе ортогональных сигналов (2). Кроме того, поскольку
на
основе элементарных сигналов вида (4) и (5) занимает в несколько раз более широкую
полосу частот, чем сигнал на основе симплексных элементарных сигналов (7) или
сигнал на основе ортогональных сигналов (2). Кроме того, поскольку ![]() , при использовании элементарных сигналов
(7) и (2) переход от передачи элементов двоичного сообщения с
, при использовании элементарных сигналов
(7) и (2) переход от передачи элементов двоичного сообщения с ![]() (отсутствует деление на блоки) к передаче
с
(отсутствует деление на блоки) к передаче
с ![]() (сообщение
делится на блоки по два элемента) не приводит к увеличению полосы частот,
занимаемой сигналом.
(сообщение
делится на блоки по два элемента) не приводит к увеличению полосы частот,
занимаемой сигналом.
3. Помехоустойчивость
Будем полагать, что на сигнал
![]() , определяемый согласно
(1), в линии связи воздействует аддитивная помеха
, определяемый согласно
(1), в линии связи воздействует аддитивная помеха ![]() в виде белого
шума с односторонней спектральной плотностью мощности N.
Поскольку сигнал
в виде белого
шума с односторонней спектральной плотностью мощности N.
Поскольку сигнал ![]() представляет
собой последовательность не перекрывающихся во времени элементарных сигналов,
то достаточно рассмотреть обработку сигнала
на входе демодулятора, соответствующего передаче какого-либо одного блока элементов
сообщения:
представляет
собой последовательность не перекрывающихся во времени элементарных сигналов,
то достаточно рассмотреть обработку сигнала
на входе демодулятора, соответствующего передаче какого-либо одного блока элементов
сообщения:
Демодулятор осуществляет
обработку сигнала (14), в результате которой должно быть принято решение, какой
из q элементарных сигналов ![]() ,
, ![]() , …,
, …, ![]() был
передан, и, следовательно, какое значение имеет принятый блок элементов
двоичного сообщения. Фактически в результате обработки в демодуляторе определяется
номер передаваемого элементарного сигнала, который будем обозначать L' (
был
передан, и, следовательно, какое значение имеет принятый блок элементов
двоичного сообщения. Фактически в результате обработки в демодуляторе определяется
номер передаваемого элементарного сигнала, который будем обозначать L' (![]() ). Если L'
не совпадает с L, то имеет место ошибка
демодуляции. Оптимальный алгоритм обработки сигнала (14), обеспечивающий
минимальную вероятность ошибки демодуляции при использовании элементарных
сигналов с одинаковой энергией имеет вид [1]:
). Если L'
не совпадает с L, то имеет место ошибка
демодуляции. Оптимальный алгоритм обработки сигнала (14), обеспечивающий
минимальную вероятность ошибки демодуляции при использовании элементарных
сигналов с одинаковой энергией имеет вид [1]:
По этому алгоритму сначала вычисляются значения 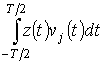 при
при ![]() . Затем
определяется j, которому соответствует максимальное из вычисленных
значений, и это j присваивается
. Затем
определяется j, которому соответствует максимальное из вычисленных
значений, и это j присваивается ![]() .
.
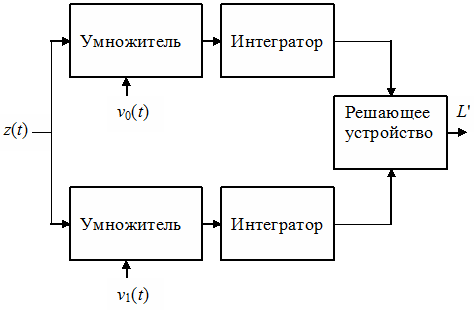
На рис. 6 показана
структура устройства, реализующего алгоритм (15) при ![]() .
Для других значений q устройство будет иметь q ветвей, каждая из которых состоит из
умножителя и интегратора, а решающее устройство будет иметь q входов. Решающее устройство оценивает
значения входных сигналов в момент времени
.
Для других значений q устройство будет иметь q ветвей, каждая из которых состоит из
умножителя и интегратора, а решающее устройство будет иметь q входов. Решающее устройство оценивает
значения входных сигналов в момент времени ![]() ,
выбирает максимальное из них и принимает решение о значении L'.
,
выбирает максимальное из них и принимает решение о значении L'.
|
|
|
Рис. 6. Структура оптимального устройства при |
При использовании ортогональных элементарных сигналов (2) вероятность ошибки демодуляции [1]
где  – функция ошибок;
– функция ошибок; ![]() ;
; ![]() – энергия, затрачиваемая на передачу
одного элемента двоичного сообщения;
– энергия, затрачиваемая на передачу
одного элемента двоичного сообщения; ![]() . При
. При ![]() (16) принимает
вид:
(16) принимает
вид: ![]() .
.
Если используются симплексные элементарные сигналы, то вероятность ошибки [2]
При ![]() сигналы (6) являются
противоположными и (17) принимает вид:
сигналы (6) являются
противоположными и (17) принимает вид: ![]() .
Для заданного значения q и
.
Для заданного значения q и
![]() симплексные
элементарные сигналы обеспечивают минимальную вероятность ошибки.
симплексные
элементарные сигналы обеспечивают минимальную вероятность ошибки.
Вероятность
ошибки демодуляции p фактически
является вероятностью ошибки при приеме блока элементов двоичного сообщения.
Если обозначить ![]() – вероятность
ошибки при приеме элемента двоичного сообщения, то можно записать [1], что
– вероятность
ошибки при приеме элемента двоичного сообщения, то можно записать [1], что ![]() , откуда
, откуда
При ![]() можно считать
можно считать ![]()
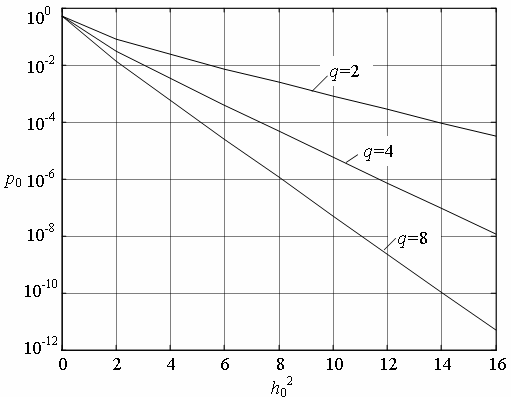
На рис. 7 показаны зависимости ![]() от
от ![]() для ортогональных элементарных сигналов при различных
значениях q, полученные по формуле (18) и (16),
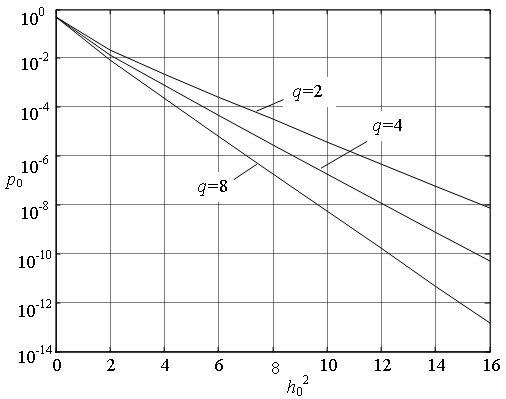
а на рис 8 – те же зависимости для симплексных сигналов, полученные по формуле
(18) и (17). На рисунках значения
для ортогональных элементарных сигналов при различных
значениях q, полученные по формуле (18) и (16),
а на рис 8 – те же зависимости для симплексных сигналов, полученные по формуле
(18) и (17). На рисунках значения ![]() , полученные при
, полученные при ![]() , для наглядности соединены отрезками
прямых.
, для наглядности соединены отрезками
прямых.
|
|
|
Рис. 7. Вероятность ошибки для ортогональных сигналов |
|
|
|
Рис. 8. Вероятность ошибки для симплексных сигналов |
Как следует из рис. 7 и
8, вероятность ошибки ![]() при фиксированном значении
при фиксированном значении ![]() с ростом
с ростом ![]() уменьшается. Это связано с
увеличением энергии элементарного сигнала
уменьшается. Это связано с
увеличением энергии элементарного сигнала ![]() за
счет увеличения его длительности. Отметим, что фиксированное значение
за
счет увеличения его длительности. Отметим, что фиксированное значение ![]() означает неизменность энергии,
затрачиваемой на передачу элемента двоичного сообщения.
означает неизменность энергии,
затрачиваемой на передачу элемента двоичного сообщения.
4. Выводы
Использование симплексных
элементарных сигналов вида (7) позволяет получить сигнал, занимающий
сравнительно узкую полосу частот. Эти элементарные сигналы целесообразно
применять при ![]() , поскольку в этом случае существенно уменьшается вероятности
ошибки
, поскольку в этом случае существенно уменьшается вероятности
ошибки ![]() без увеличения полосы частот, занимаемой сигналом, по сравнению
с
без увеличения полосы частот, занимаемой сигналом, по сравнению
с ![]() .
.
1. Теория электрической связи: Учебник для вузов / А.Г. Зюко, Д.Д. Кловский, В.И. Коржик, М.В. Назаров; Под ред. Д.Д. Кловского. – М. : Радио и связь, 1998. – 432 с.
2. Коржик В.И. и др. Расчет помехоустойчивости систем передачи дискретных сообщений: Справочник/ Коржик В.И., Финк Л.М., Щелкунов К.Н.: Под ред. Л.М. Финка.– М.: Радио и связь, 1981.– 232 с.
3. Передача дискретных сообщений/ Вершинин В.А. Рыбинская государственная авиационная технологическая академия им. П.А. Соловьева. Рыбинск, 2002.– 82 с.– Деп. в ВИНИТИ 17.12. 2002 г., № 2196-В2002.