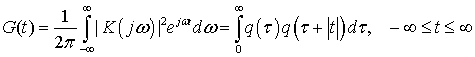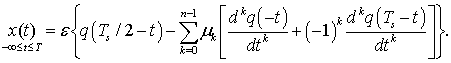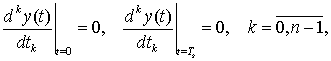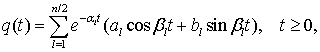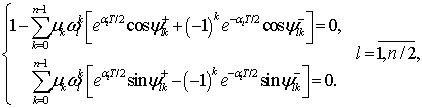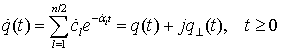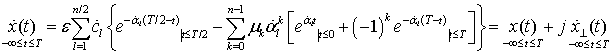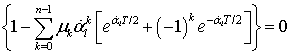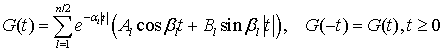МЕТОД ОПТИМИЗАЦИИ РАДИОТЕЛЕФОННОЙ СВЯЗИ

В. Г. Санников
Московский технический университет связи и информатики

Статья получена 14 ноября 2014 г.

Аннотация. В цифровой системе радиотелефонной связи с увеличением скорости передачи данных основной причиной снижения её помехозащищенности является межсимвольная интерференция. Для повышения помехозащищенности системы в современных модемах применяются в основном методы оптимизации приема, достаточно сложных в реализации на основе приема в целом. В статье предлагается новый метод синтеза оптимальных финитных сигналов в передающем модеме, принципиально не вызывающих межсимвольной интерференции на выходе канала связи, и приводящий к простому оптимальному поэлементному приему. Доказывается теорема о существовании оптимальных сигналов, финитных как на входе, так и на выходе линейного канала связи. Даются точные, по сравнению с известными соотношениями, формулы расчета помехоустойчивости радиотелефонной системы при передаче данных с квадратурной амплитудной модуляцией по каналам связи с межсимвольной интерференцией.

Основные результаты данной статьи докладывались и обсуждались на VII Всероссийской конференции «Радиолокация и радиосвязь», 25-27 ноября 2013 г.

Ключевые слова: система радиотелефонной связи, передача данных, межсимвольная интерференция, оптимальные финитные сигналы, модем, помехоустойчивость.

Abstract. In digital system of a radio telephony with magnifying of bit rate a principal cause of decrease of its noise immunity is the intersymbol interference. Methods of optimisation of reception are applied to boosting of noise immunity of system in modern modems, enough complex in implementation on the basis of the reception as a whole in the core. In paper the new method of synthesis of optimum finite signals in the transmitting modem, in essence not calling an intersymbol interference on a communication channel output, and leading to simple optimum element reception is offered. The theorem of existence of optimum signals, finite both on an entry, and on an output of a linear communication channel is proved. Formulas of calculation of a noise stability of radio-telephone system are given exact, in comparison with known parities, at a data transmission with the quadrature amplitude modulation on communication channels with an intersymbol interference.

Keywords: radio telephony system, a data transmission, intersymbol interference, optimum finite signals, the modem, a noise immunity.

1. Введение

Передача цифровых данных по радиоканалу по сравнению с коммутируемыми или арендованными каналами во многих случаях надежнее и дешевле. Сеть передачи цифровых данных с использованием радиомодемов может быть оперативно развернута практически в любом географическом районе. Под радиомодемом понимают устройство, осуществляющее модуляцию/демодуляцию цифровых данных для их передачи по радиоканалу [1]. Для передачи речевых данных используют модемы, ориентированные на использование радиотелефонного канала связи тональной частоты (РТЛФ КС), формируемого практически любой аналоговой радиостанцией КВ или УКВ диапазона. Эти модемы являются составной частью самой радиостанции, а потому должны быть оптимизированы под условия её работы.

В системах радиотелефонной связи (РТС) с увеличением скорости передачи цифровых данных основной причиной снижения помехозащищенности РТС является межсимвольная интерференция (МСИ). Для повышения помехозащищенности РТС при МСИ в современных модемах применяются в основном методы оптимизации принимаемых модемов, путем введения эквалайзеров, вносящих значительную задержку в принимаемые решения, и реализации приёма в целом с применением решающих устройств, основанных на использовании того или иного варианта алгоритма Витерби [2, 3]. Следует отметить, что помехоустойчивость этих устройств оценивается лишь приближенно, а обработка принимаемых сигналов сопряжена с высокой сложностью реализации.

В данной работе предлагается новый подход при организации РТС, основанный на оптимизации не только приемника системы РТС, но и передатчика, путем синтеза оптимальных (финитных как на входе, так и на выходе РТЛФ КС) сигналов в передающем модеме, принципиально не вызывающих МСИ на приеме. Приводится доказательство существования оптимальных финитных сигналов (ОФС) для частотно-ограниченного линейного канала связи с комплексно-сопряженными корнями. При передаче ОФС по РТЛФ КС обеспечивается простой оптимальный их поэлементный прием на согласованный фильтр (СФ), позволяющий точно оценивать помехоустойчивость систем РТС с многопозиционными сигналами квадратурной амплитудной модуляции (КАМ).

2. Система радиотелефонной связи с квадратурной амплитудной модуляцией

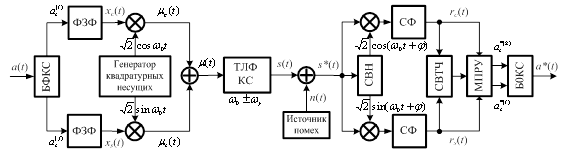
Модель РТС с КАМ рассмотрена в работах [4, 5] и показана на рисунке 1.

Рис. 1 – Модель системы радиотелефонной связи с квадратурной амплитудной модуляцией

Здесь введены следующие сокращения. В модуляторе БФКС – блок формирования квадратурных сообщений, ФОС – формирователь оптимальных сигналов; в демодуляторе СВН – система восстановления несущей, СФ – согласованный фильтр, СВТЧ – система восстановления тактовой частоты, МПРУ – многопороговое решающее устройство, БОКС – блок объединения квадратурных сообщений. Полагается, что СВН и СВТЧ обеспечивают идеальную синхронизацию РТС.

В системе, изображенной на рисунке 1, последовательность независимых и равновероятных двоичных сообщений , в блоке БФКС путем соответствующего объединения двоичных символов преобразуется в две независимые последовательности символов многоуровневой амплитудной модуляции (МАМ) с .

Квадратурные символы МАМ представляют собой стационарные последовательности случайных равновероятных величин с нулевым средним, принимающих в интервалах , где , кусочно-постоянные значения:

, . (1)

Расстояние между сигнальными точками равно и характеризует энергетическую базу сигнала КАМ [3].

Сигнал КАМ на выходе модулятора, с учетом квадратурных несущих сдвинутых по фазе на , принимает вид

, (2)

а полезная составляющая отклика РТЛФ КС равна

, (3)

где - центральная частота, - фазовый сдвиг, вносимый каналом связи, и - соответственно, сигналы на входе и выходе низкочастотного эквивалента (НЧЭ) РТЛФ КС, подлежащие определению и оптимизации.

3. Постановка задачи оптимизации модема

Основная задача оптимизации модулятора состоит в том, чтобы при известной импульсной реакции НЧЭ РТЛФ КС , осуществить синтез таких финитных во времени сигналов , и , которые на входе СФ демодулятора обеспечивают максимум отношения сигнал шум (ОСШ) в середине посылки, т.е. в момент . При фиксированной мощности шума, критерий оптимальности записывается в виде

. (4)

где – спектральная плотность комплексных амплитуд (СПКА) сигнала, а - комплексный коэффициент передачи НЧЭ РТЛФ КС.

Такого вида сигналы названы оптимальными финитными сигналами (ОФС) [4]. Синтез оптимального по критерию (4) сигнала , формируемого в блоке (ФОС) (см. рисунок 1), осуществлен в работе [4] на основе решения вариационной задачи на условный экстремум. Показано, что ОФС согласован с импульсной реакцией НЧЭ РТЛФ КС и не вызывает МСИ на его выходе. При этом ОФС , наблюдаемый на выходе НЧЭ РТЛФ КС, согласован с его канальной функцией , определяемой так

. (5)

В работе [4] получены следующие соотношения для искомых ОФС

(6)

(7)

Здесь величина определяется из условия ограничения на энергию ОФС

, (8)

а величины - множители Лагранжа решения вариационной задачи, удовлетворяющие следующим ограничениям во временной области

(9)

Заметим, что в работе [4] утверждается, но не доказывается, что соотношения (6) и (7) справедливы на финитном интервале , и равны нулю вне этого интервала.

В данном исследовании приведем доказательство этого утверждения.

4. Оптимальные финитные сигналы для линейного канала связи с различными комплексно сопряженными корнями

Модель и характеристики низкочастотного эквивалента РТЛФ КС. В системах цифровой радиотелефонии в качестве НЧЭ фильтров, входящих в состав канала связи, часто используются фильтры Баттерворта ого порядка [6], квадрат передаточной функцией которых определяется соотношением

, (10)

где - частота среза, определяемая по уровню ослабления на 3 дБ.

Корни характеристического уравнения линейного канала связи с передаточной функцией (10), как нетрудно показать, являются комплексно-сопряженными вида:

, . (11)

Для модели КС, характеристическое уравнение которого имеет комплексно-сопряженные корни: , его импульсную реакцию , на основе теории линейных дифференциальных уравнений [7], можно представить в виде

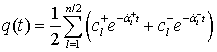. (12а)

где - постоянные интегрирования дифференциального уравнения КС, сумма и разность которых соответственно равны: , .

Соотношение (12а) приводится к эквивалентному виду

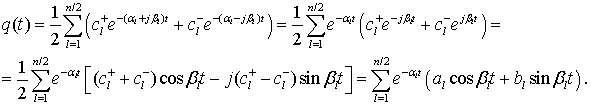(12б)

Условия финитности оптимальных сигналов. Результаты данного исследования представим в виде следующей теоремы.

Теорема 1. Пусть рассматривается модель низкочастотного эквивалента канала связи, характеристическое уравнение которого определяется различными комплексно-сопряженными корнями , а импульсная реакция равна

(13)

где и - постоянные интегрирования дифференциального уравнения модели НЧЭ КС, определяемые из начальных условий.

Тогда сигналы в (6) на входе и в (7) на выходе НЧЭ КС с импульсной реакцией (13), удовлетворяющие критерию (4), будут оптимальными финитными сигналами, определенными на интервале , если множители Лагранжа в (6) и (7) удовлетворяют следующей системе из неоднородных линейных уравнений

(14)

Здесь введены следующие обозначения

, , , , . (15)

Доказательство.

1. Введем комплексную импульсную реакцию исследуемого канала

, (16)

где - комплексные постоянные, - мнимая часть , а - её реальная часть, определяемая по соотношению (13), т.е. .

Заменяя в соотношении (6) действительные функции на комплексные, находим комплексный сигнал на входе НЧЭ КС в виде

(17)

Для подтверждения соотношения (14), обеспечивающего условие финитности сигнала на интервале , вынесем в (17) за фигурные скобки функцию , которая при не равна нулю. В результате получаем

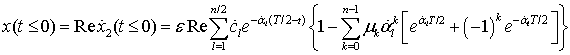Очевидно, что сигнал будет равен нулю тогда и только тогда, когда соотношение в фигурных скобках полученного соотношения будет равно нулю, т.е.

. (18)

С учетом обозначений в (15), соотношение (18) приводится к следующему виду

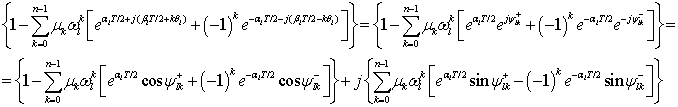
где учтены соотношения: , где , .

Приравнивая действительную и мнимую части этого соотношения нулю, приходим к соотношению (14). Отсюда заключаем, что комплексный сигнал в (17) полностью определен на финитном интервале и равен нулю вне этого интервала, а его действительная компонента приводится к виду

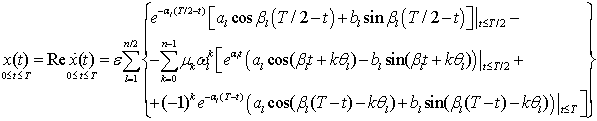. (19)

Итак, искомый сигнал , есть ОФС по критерию максимума (4); он согласован с импульсной реакцией НЧЭ КС в (13) и полностью определяется соотношением (19) на временном интервале .

2. Найдем теперь отклик НЧЭ КС . Для этого вначале определим канальную функцию в (5) с учетом импульсной реакции (13). Подставляя (13) в (5), с учетом обозначений: , , получаем

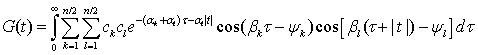Используя таблицы интегралов [8], приводим канальную функцию к виду:

, (20)

где введены следующие обозначения:

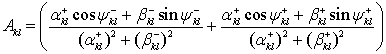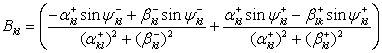Используя комплексные величины: , от действительной канальной функции (20) переходим к комплексному её представлению

. (21)

С учетом (7), находим производные от функции

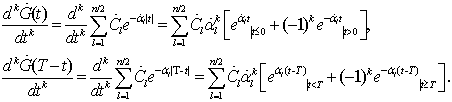
. (22)

Подставляя (21) и (22) в (7), находим комплексный отклик НЧЭ КС в виде

(23)

Покажем, что в (23) . Учитывая все компоненты для временных моментов и вынося за фигурные скобки функцию , которая для всех не равна нулю, с учетом равенства (18) получаем

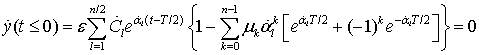. (24)

Покажем также, что в (23) . Так, учитывая все компоненты для временных моментов и вынося в (23) за скобки функцию , которая для всех не равна нулю, с учетом равенства (18) получаем

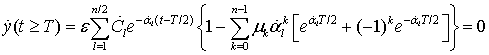. (25)

Следовательно, сигнал , есть ОФС по критерию максимума (4); он согласован с канальной функцией (20) и полностью определяется соотношением (23) на финитном интервале .

Переходя в (23) от комплексного к действительному сигналу получаем выражение для реального отклика НЧЭ КС в виде

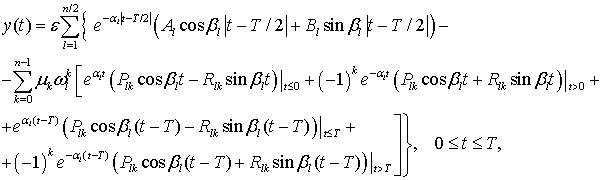(26)

где

Итак, поставленная задача по синтезу финитного сигнала , сохраняющего также финитным отклик канала , и максимизирующего мгновенное значение этого отклика в момент по критерию (4), полностью решена для каналов с комплексно-сопряженными корнями и импульсной реакцией вида (16).

3. Для окончательного доказательства существования на конечном интервале ОФС на входе и выходе НЧЭ КС с импульсной реакцией (16) требуется проверить выполнимость ограничений (9), налагаемых на производные отклика НЧЭ КС. Так для комплексного отклика НЧЭ КС вида (23) искомые производные равны

(27)

Подставляя в (27) , проверим первое условие в (9)

(28)

Подставляя в (27) , проверим второе условие в (9)

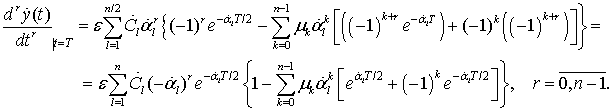(29)

С учетом равенства (18), анализ полученных соотношений (28) и (29) показывает, что введенные в (9) ограничения на производные отклика НЧЭ КС будут выполняться, если множители Лагранжа , удовлетворяют равенству (18) и находятся из решения системы неоднородных линейных уравнений вида (14).

Итак, поставленная задача синтеза ОФС , сохраняющего финитным отклик канала , и максимизирующего мгновенное значение отклика НЧЭ КС в момент , полностью решена для модели НЧЭ КС с комплексно-сопряженными некратными корнями и импульсной реакцией вида (16).

Отсюда следует, что финитность ОФС на входе и выходе НЧЭ КС приводит к отсутствию межсимвольных искажений при последовательной передаче дискретных сообщений в цифровых радиотелефонных системах.

Теорема 1 доказана.

5. Оптимальные финитные сигналы для линейного канала связи типа фильтра Баттерворта

Для НЧЭ канала, построенного на основе фильтра Баттерворта, с передаточной функцией вида (10) и корнями из (11), импульсная реакция и её производные , а также канальная функция и её производные , соответственно, равны [4]:

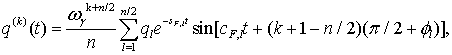
(30)

(31)

где , и, кроме того, в (30) и (31) введены обозначения:

, , , , , .

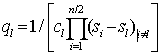Множители Лагранжа, удовлетворяющие системе линейных уравнений (14), применительно к НЧЭ КС типа фильтра Баттерворта находятся из более простого соотношения [5]

, (32)

где , .

Спектры ОФС и , соответственно, равны [4]:

, , (33)

где - сигнальная функция, определяемая по соотношению

. (34)

Графики оптимальных финитных сигналов и их спектров на входе и выходе фильтра Баттерворта с , (кГц) при (мс) показаны на рисунке 2.

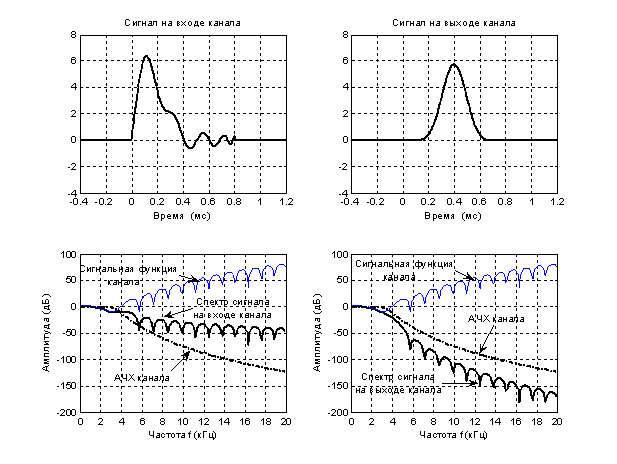
Рис 2. – Графики форм и спектров ОФС на входе и выходе фильтра Баттерворта

6. Помехоустойчивость оптимального когерентного модема

На вход демодулятора РТС (см. рисунок 1) воздействует смесь полезного сигнала и шума , где полагается, что - есть стационарный аддитивный белый гауссовский шум (АБГШ) с нулевым средним значением и односторонней спектральной плотностью мощности . На выходе перемножителей с квадратурными опорными колебаниями наблюдаются квадратурные сигналы следующего вида

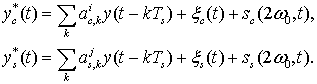(35)

где и - стационарные аддитивные белые гауссовские шумы с нулевыми средними и односторонней спектральной плотностью мощности , а и - квадратурные компоненты на удвоенных центральных частотах, которые на выходах последующих низкочастотных фильтрах подавляются.

Поскольку ОФС , финитен во времени, наблюдается на фоне АБГШ, то прием его в демодуляторе осуществляется поэлементно на оптимальный линейный согласованный фильтр (СФ) с импульсной реакцией вида: . При этом отклики СФ и (- энергия ОФС) в моменты , вычисляемые в блоке СВТЧ, поступают на многопороговое решающее устройство (МПРУ) для получения оценок и квадратурных величин, определенных в (1).

Важным параметром случайных величин и , формируемых в модуляторе, является средняя мощность

. (36)

В системе РТС с ограниченным энергоресурсом сравнение дискретных ансамблей проводят по величине коэффициента помехоустойчивости: . Отсюда величину в (36) можно представить в виде

. (37)

С учетом (33) и (34) для КС с фильтром Баттерворта введем коэффициент передачи по энергии (КПЕ)

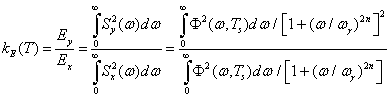. (38)

Описанная выше обработка наблюдаемого на приеме сигнала в двух квадратурных каналах демодулятора с КАМ одинакова. При КАМ в МПРУ должны выноситься совместные решения о передаваемых символах и на множестве .

Предполагая, что все сигнальные точки равновероятны, среднее ОСШ при приеме сигналов КАМ определяется формулой

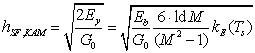. (39)

где - энергия ОФС , - длительность символа, - длительность бита, - энергия, приходящаяся на один бит передаваемых данных, .

При этом средняя вероятность ошибки на символ при приеме сигнала КАМ определяется следующим соотношением [9]:

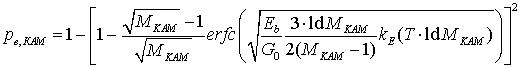, (40)

Средняя вероятность ошибки, приходящая на один информационный бит, соответственно равна: .

Соотношения (38)-(40) определяют потенциальную помехоустойчивость оптимального когерентного модема с КАМ в системе РТС.

Зависимости от ОСШ и скорости передачи для , равных 4x4, 8x8, 16x16, показаны на рисунке 3. Здесь , .

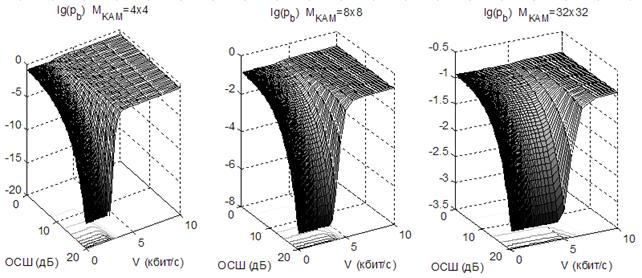
Рис. 3 – Графики помехоустойчивости оптимального когерентного модема с КАМ

На рисунке 4 приведены зависимости вероятностей ошибки на символ (штрих-пунктир) и на бит (сплошные), определяющие сечения зависимостей из рисунка 3. Здесь на левом графике приведены зависимости вероятностей ошибок от отношения энергии на бит к односторонней спектральной плотности мощности АБГШ при фиксированной скорости , а правый график иллюстрирует зависимости вероятностей ошибок от скорости передачи при фиксированном отношении .

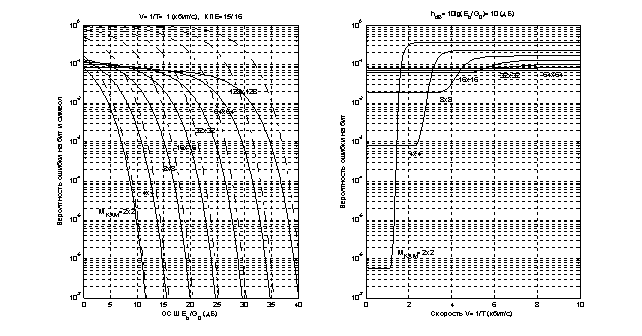
Рис. 4 – Графики зависимости вероятностей ошибок от ОСШ и скорости передачи

7. Заключение

Результаты настоящего исследования применимы к анализу потенциальной помехоустойчивости системы цифровой РТС с КАМ. Здесь по заданным или, полученным экспериментально, характеристикам (импульсной реакции или передаточной функции) радиотелефонного канала связи синтезируются как на входе, так и на выходе канала, оптимальные, финитные во времени сигналы, не вызывающие межсимвольной интерференции и обеспечивающие максимум отношения сигнал/шум на входе решающего устройства приемника или минимум средней вероятности ошибки на его выходе. Вместо сложного приема в целом в данном случае реализуется простой поэлементный прием без задержки во времени принятия решений, что значительно сокращает время вхождения в связь при организации взаимодействия передающего и приемного интеллектуальных модемов, разработке которых в настоящее время уделяется очень большое внимание.

Литература

1. Лагутенко О.И. Современные модемы. – М.: Эко-Трендз, 2002. – 343 с.

2. Зяблов В.В., Коробков Д.Л., Портной С.Л. Высокоскоростная передача сообщений в реальных каналах. – М.: Радио и связь, 1991. – 288 с.

3. Прокис Дж. Цифровая связь: Пер. с англ. / Под ред. Д.Д. Кловского. – М.: Радио и связь, 2000. – 800 с.

4. Санников В.Г. Синтез финитных сигналов Найквиста, согласованных с телефонным каналом связи // «ЭЛЕКТРОСВЯЗЬ», № 5, 2012. – С. 9 – 12.

5. Санников В.Г. Метод оптимизации радиотелефонной связи // Доклады VII Всероссийской научно-технической конференции «Радиолокация и радиосвязь», 25-27 ноября 2013 г., Москва. – С. 108–112.

6. Феер К. Беспроводная цифровая связь. Методы модуляции и расширения спектра: Пер. с англ. / Под ред. В.И. Журавлева. – М.: Радио и связь, 2000. – 520 с.

7. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения: Учеб. для вузов. – 4-е изд. – М.: ФИЗМАТЛИТ, 2005. – 256 с. (Курс высшей математики и математической физики. – Вып. 6).

8. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. – М.: «НАУКА», ГР ФМЛ, 1971. – 1108 с.

9. Санников В.Г. Помехоустойчивость системы передачи оптимальных финитных сигналов по телефонному каналу связи // «ЭЛЕКТРОСВЯЗЬ», № 5, 2013.– С. 39–44.