УДК 537.87, 621.396.67
Проволочная структура с эффектом отрицательного преломления в СВЧ диапазоне
Д. А. Павлов 1, Л. Н. Бутько 1, А. А. Федий 1, А. П. Анзулевич 1, И. В. Бычков 1, В. Д. Бучельников 1, В. Г. Шавров 2
1 Челябинский Государственный университет
2 Институт радиотехники и электроники им. В.А. Котельникова РАН
Статья поступила в редакцию 31 октября 2015 г.
Аннотация. В работе рассмотрен электромагнитный кристалл, состоящий из прямолинейных длинных проволок (стержней), образующих двухмерную квадратную решетку внутри диэлектрической матрицы. Показано, что данный кристалл в небольшой полосе частот подобен квазиоднородной среде с одновременно отрицательными магнитной и электрической проницаемостями. Продемонстрирован эффект отрицательного преломления в СВЧ диапазоне. Частотные диапазоны, на которых электромагнитный кристалл проявляет эффекты положительного и отрицательного преломления, соответствуют зонной структуре, полученной численно и экспериментально.
Ключевые слова: проволочные структуры, электромагнитные кристаллы, отрицательное преломление, метаматериалы.
Abstract: In this paper we consider the electromagnetic crystal consisting of long, straight wires (rods) forming a two-dimensional square lattice in the dielectric matrix. It is shown that the crystal in a small band is like a quasi-homogeneous medium with simultaneously negative electrical and magnetic permeabilities. The effect of negative refraction at microwave frequencies is demonstrated. The frequency ranges in which the electromagnetic crystal exhibits the effects of positive and negative refraction, corresponds to band structure obtained numerically and experimentally.
Keywords: wire structure, electromagnetic crystal, negative refraction, permittivity, metamaterials.
Введение
Почти во всех естественных и композитных средах на частотах, представляющих интерес, диэлектрическая и магнитная проницаемости равны или больше единицы. Если диэлектрическая, либо магнитная проницаемость отрицательна, но не обе одновременно, то электромагнитные поля не могут распространяться, и экспоненциально затухают в такой среде. Подходящим примером среды, которая может быть прозрачной и непрозрачной, является проволочная среда [1], в которой диэлектрическая проницаемость зависит от частоты:
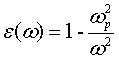(1)
где ωр - параметр, зависящий от плотности, заряда и массы носителей заряда; этот параметр обычно называется плазменной частотой. Для этого случая μ предполагается равной единице для всех частот. Ниже плазменной частоты диэлектрическая проницаемость отрицательна, и электромагнитные волны не могут в ней распространяться. Выше плазменной частоты диэлектрическая проницаемость является положительной, и электромагнитные волны могут распространяться через такую среду.
В 1967 году Веселаго рассмотрел теоретически необычные свойства среды, в которой и ε(ω) и μ(ω) будут одновременно отрицательными, и проанализировал, каким образом электромагнитные волны распространялись бы в этих средах [1]. Он пришел к выводу, что распространение волн в среде с одновременно отрицательными ε(ω) и μ(ω),будет принципиально отличаться от среды, в которых ε(ω) и μ(ω) являются положительными.
В обычных средах, когда обе проницаемости
ε(ω) и μ(ω) одновременно положительны, направление потока
энергии совпадает с направлением фазовой скорости (или волнового вектора k) и вектора
E,H,k образуют правую тройку векторов. Такие среды принято называть правыми.
При отрицательных ε(ω) и μ(ω) направления распространения
фазовой и групповой скоростей противоположны, и вектора Е,H,k образуют левую
тройку векторов. Веселаго назвал среды с одновременно отрицательными
ε(ω) и μ(ω) левыми средами (LHM). Кроме того, Веселаго
предположил, что коэффициент преломления n(ω), который используется в
интерпретации уравнений Максвелла, следует рассматривать как 
. Таким образом, левые среды могут
называться средами с отрицательным показателем преломления среды.
Новым толчком к развитию данного направления и началом современного этапа в формировании теоретических представлений о LHM-средах послужила публикация Джона Пендри [2], в которой было предложено использовать искусственно созданные материалы, обладающие отрицательными эффективными значениями диэлектрической и магнитной проницаемостей.
Ранее в экспериментальных и теоретических работах
было показано, что фотонные кристаллы обладают зонной структурой спектра [3–4].
Из данных работ видно, что в области частот, где отношение периода решетки к
длине волны электромагнитного поля внутри диэлектрической матрицы a/λ<0.25,
эффективная электрическая проницаемость 
отрицательна
(т.к. ω<ωp) и электромагнитные поля не могут
распространяться в такой среде. Однако в интервале 0.3<a/λ<1
поведение эффективных магнитной и электрической проницаемостей является
аномальным. При 0.3<a/λ<0.5 электрическая проницаемость
положительна [3], и проволочная структура пропускает электромагнитное излучение
[4]. При 0.5<a/λ<0.65 структура не прозрачна. А при a/λ>0.65
структура снова пропускает электромагнитное излучение. Исходя из работы [5],
где для фотонного кристалла треугольной решетки во второй разрешенной зоне
обнаружено отрицательное преломление, мы предполагаем, что и в нашем случае в
данной области будет отрицательное преломление, следовательно, обе
проницаемости будут отрицательны.
В данной работе экспериментально определен диапазон первых двух зон пропускания в области 0.1<a/λ<1 для фотонного кристалла с квадратной решеткой. Показано, что на любых частотах первой зоны прозрачности наблюдается положительное преломление, а для частот второй зоны наблюдается отрицательное преломление, т.е. проницаемости одновременно отрицательны. Параллельно проведено численное моделирование и показано согласование численных и экспериментальных результатов.
1. Метод исследований
Исследования проводились в диапазоне 8 – 13 ГГц, для демонстрации обеих (0.3<a/λ<0.5 и a/λ>0.65) зон пропускания было изготовлены две прямоугольные пластины проволочной среды (рис. 1a.) из массива цилиндрических медных стержней длиной 12 мм и радиусом 0,35 мм, образующих квадратную решетку в диэлектрической матрице. Период решетки для первого образца, в котором исследуется первая зона, брался a=0.7 см, и для второго образца a=1.2 см. Диэлектрическая матрица – гипс (CaSO4·2H2O). Для демонстрации положительного и отрицательного преломления были изготовлены образцы в виде преломляющих призм с периодами решетки соответственно a=0.7 см и a=1.2 см (рис. 1b.).
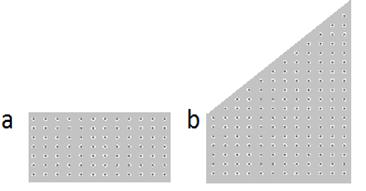
Рис.1. Геометрия исследуемых образцов
Прототип исследовательской установки описан в работе [6], а описание установки, на которой проводились измерения, приведено в работе [7]. Она состоит из трех основных блоков: скалярного анализатора цепей Р2М-40, работающего в диапазоне от 10 МГц до 40 ГГц, формирователя направленного узкого пучка СВЧ излучения, плоской угловой камерой для исследуемых образцов, состоящей из двух медных пластин, а также ПК. Из-за поглощения электромагнитного излучения на стенках формирователя опорный уровень равен –24dB.
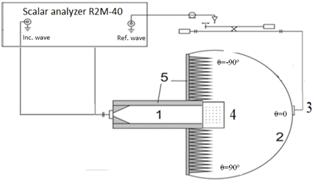
Рис. 2. Экспериментальная установка.
1 –формирователь пучка, 2 – измерительная камера, 3 – детекторная секция, 4 – исследуемый образец, 5 – поглотитель.
Данный спектрометр позволяет измерять коэффициент прохождения СВЧ–излучения в диапазоне углов от -90 до +90 градусов на частотах 8 – 13 ГГц.
2. Численные исследования
Путем численного моделирования были получены двухмерные картины распределения электромагнитного поля внутри волновода и в образцах (Рис 6, 9). Электрическая напряженность волны получена численным решением уравнения (2) при соответствующих граничных условиях.
, (2)
где ε, μ, σ – локальные диэлектрическая проницаемость, магнитная проницаемость и проводимость соответственно, k0 = ω/c– волновое число в вакууме, ε0 = 8,85*10-12 Ф/м – электрическая постоянная. Решение уравнения (2) в точках наблюдения внутри композитного слоя находится прямым численным методом конечных элементов с учетом граничных условий. Сетка разбиения на конечные элементы задается таким образом, чтобы размер ячейки был много меньше размера неоднородностей, размера структурных элементов композита (радиуса стержней), локальной длины электромагнитной волны и толщины скин-слоя. Используемый метод численного решения уравнения (2) позволяет учесть внутреннюю структуру композита, в том числе получить детальное распределение электромагнитного поля в исследуемой структуре, с учетом взаимного поляризующего, намагничивающего воздействия каждого структурного элемента (стержня) друг на друга и с учетом эффекта запаздывания поляризации, намагниченности по отношению к изменению электромагнитного поля.
3. Результаты экспериментов и численного моделирования
3.1 Экспериментально были получены зависимости коэффициента прохождения волны от частоты и от параметра a/λ через прямоугольные образцы проволочных сред с постоянными решетки 7мм и 12мм (рис.3).
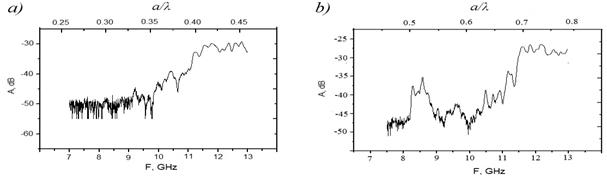
Рис. 3. Коэффициент пропускания пластины из проволочной среды с периодом 7мм(a) и 12мм(b).
Хорошо видно наличие зон прозрачности для каждого из образцов. Для уточнения полученных результатов был изготовлен проверочный образец с постоянной решетки 10.5мм, в котором были обнаружены 2 зоны прозрачности (рис. 4.), данный результат согласуется с имеющимися данными [3].
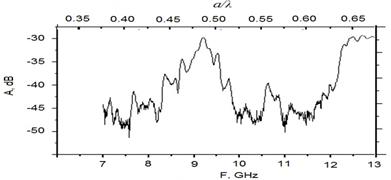
Рис. 4. Коэффициент пропускания пластины с a=10.5мм.
3.2 В ходе эксперимента и численного моделирования для образца в виде преломляющей призмы с периодом решетки a = 7мм было обнаружено, что на частотах из первого диапазона, соответствующих 0.3<a/λ<0.5, электромагнитная волна при прохождении через призму испытывает положительное преломление θ> -45º.
На рисунке 5 показаны экспериментальные (a) и численные (b) зависимости интенсивности прошедшей волны от угла θ на ряде частот, при которых максимум интенсивности наблюдается при θ≈0, т.е. волна не преломляется и коэффициент преломления n≈1.
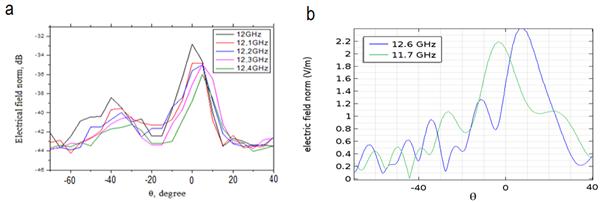
Рис. 5. Результаты эксперимента (a) и численного моделирования (b).
На рисунке 6 показано распределение электромагнитного поля для данного случая с n≈1 на одной частоте.
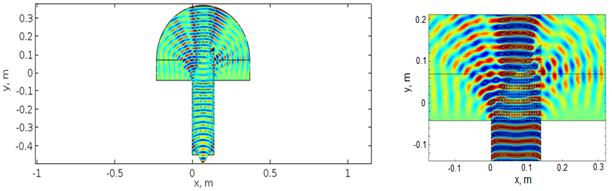
Рис. 6. Численный расчет распределения поля в проволочной структуре с постоянной решетки a = 7мм
3.3 Из эксперимента и численного моделирования для образца в виде преломляющей призмы с периодом решетки a = 12 мм было обнаружено, что на частотах из второго диапазона a/λ>0.65 электромагнитная волна при прохождении через призму испытывает отрицательное преломление θ< –45º. Данный эффект наиболее четко виден на картинах распределения в середине второй зоны (при a/λ=0.75 и f=12.6GHz), т.к. волна меньше всего отражается от образца. На рисунке 7 показана зависимость интенсивности прошедшей волны от угла θ на частотах из середины второй зоны.
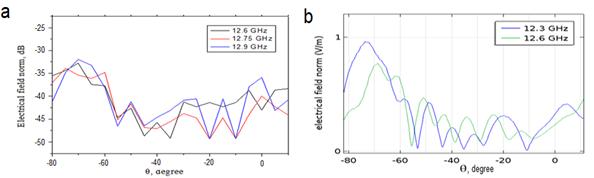
Рис. 7. Результаты эксперимента (a) и численного моделирования (b)
На рисунке 8 показано распределение электромагнитного поля для случая отрицательного преломления (θ<-45º) на нескольких близких частотах из середины второй зоны, где данный эффект отрицательного преломления более нагляден.
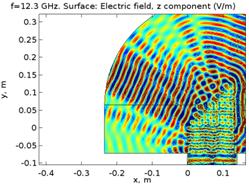
Рис. 8. Численный расчет распределения поля в проволочной структуре
Отрицательное преломление (θ<-45º) микроволнового излучения в проволочной структуре во второй зоне прозрачности с 0.65<a/λ<1.
Заключение
Мы показали, что исследуемый нами фотонный кристалл подобен однородной среде с одновременно отрицательными магнитной и электрической проницаемостями. Продемонстрировали эффект отрицательного преломления в СВЧ диапазоне. Частотные диапазоны, на которых фотонный кристалл проявляет эффекты положительного и отрицательного преломления, соответствуют зонной структуре, полученной численно и экспериментально.
Продемонстрирован эффект положительного и отрицательного преломления в СВЧ диапазоне. Определены границы частотных диапазонов этих эффектов и показано, что они совпадают с соответствующей с зонной структурой коэффициента пропускания ЭМВ в размерности a/λ.
Работа выполнена при поддержке гранта РФФИ 15-07-08111A.
Литература
1. Веселаго В.Г. Электродинамика веществ с одновременно отрицательными значениями ε и μ. УФН т. 92 с. 517–526 (1967).
2. J.B. Pendry et al. Magnetism from conductors and enhanced nonlinear phenomena. – IEEE Trans. Microw. Theory Tech., Vol. 47, No.11, 1999, pp. 2075–2084.
3. P.A. Belov, S.A. Tretyakov, A.J., Viitanen. J. Dispersion and reflection properties of artificial media formed by regular lattices of ideally conducting wires, Waves and Appl. 2002. Vol.16. № 8, pp. 1153-1170.
4. И.В. Бычков, И.С. Зотов, А.А. Федий. Исследование амплитудно-частотной характеристики коэффициента пропускания двумерного электромагнитного кристалла, образованного медными цилиндрами. Письма в ЖТФ, 2011, том 37, вып. 23.
5. P.V. Parimi et al. Negative Refraction and Left-Handed Electromagnetism in Microwave Photonic Crystals, Physical Review Letters, Vol. 92, No. 12, 22 March 2004, p. 127401.
6. Starr A.F., Rye P.M., Mock J.J., Smith D.R. Angle resolved microwave spectrometer for metamaterials studies, Review of Scientific Instruments. Vol. 75, №4. P.820-825
7. И. В. Бычков, Д. В. Дубровских, И. С. Зотов, Д. А. Павлов, А. А. Федий, В. Г. Шавров. Угловой спектрометр для исследования метаматериалов. // Журнал радиоэлектроники: электронный журнал. 2011. N5. URL: http://jre.cplire.ru/alt/may11/6/text.pdf